1、温州市平阳县、苍南县、泰顺县温州市平阳县、苍南县、泰顺县 2020 届九年级学业水平适应性考试数学试卷届九年级学业水平适应性考试数学试卷 一、选择题一、选择题(本题有本题有 10 小题，每小题小题，每小题 4 分，共分，共 40 分分.) 1.-5 的相反数是( ) A. 5 B. -5 C. D. 2.2020 年春节之际，新冠肺炎疫情突如其来，危难时刻，42000 多名医务工作者从全国各地驰援湖北，他 们都是最美的“逆行者”，其中数据 42000 用科学计数法表示为( )。 A. 0.42105 B. 4.2104 C. 42103 D. 4.2103 3.由一个长方体和一个球组成的几何体
2、如图所示，它的主视图是( ) A. B. C. D. 4.一个不透明的袋中，装有 2 个黄球、3 个红球和 5 个白球，它们除颜色外都相同从袋中任意摸出一个 球，是白球的概率是（ ） A. B. C. D. 5.若关于 x 的一元二次方程 4x-4x+c=0 有两个相等实数根，则 c 的值是( ) A. -1 B. 1 C. -4 D. 4 6.不等式组 * 的解是( ) A. x-1 C. -1x4 7.如图，梯子 AC 的长为 2.8 米，则梯子顶端离地面的高度 AD 是( ) A. 米 B. 米 C. sin 米 D. cos 米 8.某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙(
3、墙足够长)，并在如图所示位置留 2m 宽的门。 已知计划中的建筑材料可建围墙(不包括门)的总长度为 50m。设饲养室长为 x(m)，占地面积为 y(m)，则 y 关于 x 的函数表达式是( ) A. y=-x+50x B. y= x+24x C. y= x 2+25x D. y= x 2+26x 9.已知反比例函数 y= (k0)，当-2x-1 时，y 的最大值是 3，则当 x6 时，y 有( ) A. 最大值 B. 最大值-1 C. 最小值 D. 最小值-1 10.我国古代伟大的数学家刘徽于公元 263 年撰九章算术注中指出，“周三径一”不是圆周率值，实际上 是圆内接正六边形周长和直径的比值
4、(图 1)。刘徽发现，圆内接正多边形边数无限增加时，多边形的周长就 无限逼近圆周长，从而创立“割圆术”，为计算圆周率建立起相当严密的理论和完善的算法。如图 2，六边 形 ABCDEF 是圆内接正六边形，把每段弧二等分，作出一个圆内接正十二边形，连结 AG，CF，AG 交 CF 于 点 P，若 AP=2 ，则 的长为( ) A. B. C. D. 二、填空题二、填空题(本题有本题有 6 小题，每小题小题，每小题 5 分，共分，共 30 分分) 11.分解因式：m2-2m=_。 12.一组数据 1，2，x，5，8 的平均数是 5，则该组数据的中位数是_。 13.计算 的结果是_。 14.如图，PA
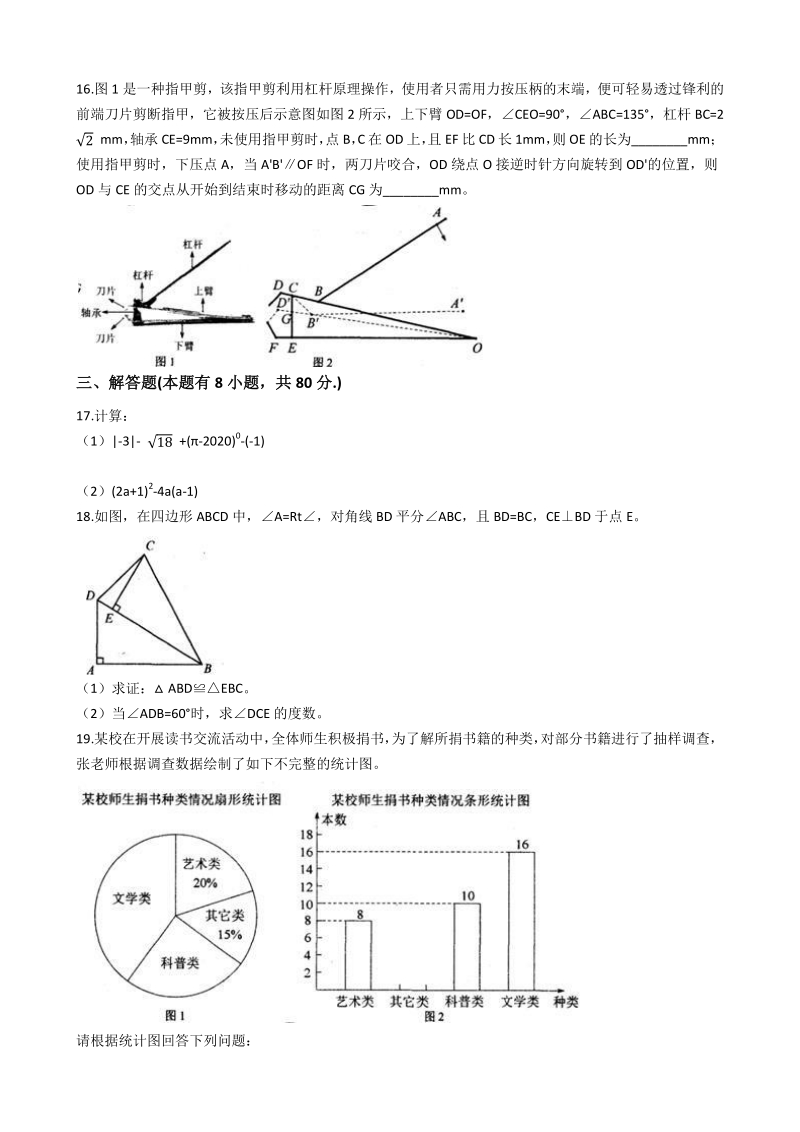
5、，PB 是O 的切线，A，B 为切点，点 C 在O 上，且ACB=55，则APB 等于_度。 15.如图，在 ABC 中，分别以 AB，AC 为边向外作正方形 ABED，ACGF。若点 E，A，G 在同一直线上，EG=8 ，BC=7，则 ABC 的面积为_。 16.图 1 是一种指甲剪，该指甲剪利用杠杆原理操作，使用者只需用力按压柄的末端，便可轻易透过锋利的 前端刀片剪断指甲，它被按压后示意图如图 2 所示，上下臂 OD=OF，CEO=90，ABC=135，杠杆 BC=2 mm， 轴承 CE=9mm， 未使用指甲剪时， 点 B， C 在 OD 上， 且 EF 比 CD 长 1mm， 则 OE
6、的长为_mm； 使用指甲剪时，下压点 A，当 ABOF 时，两刀片咬合，OD 绕点 O 接逆时针方向旋转到 OD的位置，则 OD 与 CE 的交点从开始到结束时移动的距离 CG 为_mm。 三、解答题三、解答题(本题有本题有 8 小题，共小题，共 80 分分.) 17.计算： （1）|-3|- +(-2020)0-(-1) （2）(2a+1)2-4a(a-1) 18.如图，在四边形 ABCD 中，A=Rt，对角线 BD 平分ABC，且 BD=BC，CEBD 于点 E。 （1）求证： ABDEBC。 （2）当ADB=60时，求DCE 的度数。 19.某校在开展读书交流活动中， 全体师生积极捐书，
7、 为了解所捐书籍的种类， 对部分书籍进行了抽样调查， 张老师根据调查数据绘制了如下不完整的统计图。 请根据统计图回答下列问题： （1）本次抽样调查的书籍有多少本？ （2）试求图 1 中表示文学类书籍的扇形圆心角的度数，并补全条形统计图。 （3）本次活动师生共捐书 1600 本，请估计有多少本科普类书籍？ 20.如图，在方格纸中，点 A，B 都在格点上，请按要求画图。 （1）在图 1 中画出一个以 AB 为腰的格点等腰 ABC。 （2）在图 2 中画出一个以 AB 为边的格点 ABCD，且其中一个内角为 45。 21.如图，抛物线 y=-x+bx+4 交 y 轴于点 B，顶点为 M，BAy 轴，
8、交抛物线于点 A。已知该抛物线的对称 轴为直线 x= 。 （1）求 b 的值和点 M 的坐标。 （2） 将抛物线向下平移 m 个单位， 使平移后得到的抛物线顶点落在 OAB 的内部(不包括 OAB 的边界)， 则 m 的取值范围为_。 22.如图，在 ABC 中，ACB=90，点 D 在 BC 边上(不包括端点 B，C) ，过 A，C，D 三点的O 交 AB 于 另一点 E，连结 AD，DE，CE，且 CEAD 于点 G，过点 C 作 CFDE 交 AD 于点 F，连结 EF。 （1）求证：四边形 DCFE 是菱形。 （2）当 tanAEF= ，AC=4 时，求O 的直径长。 23.下表是小丽
9、在某路口统计 20 分钟各种车辆通过情况的记录表，其中空格处的字迹已模糊。 电瓶车 公交车 货车 小轿车 合计(车流总量) (第一时段)8：509：00 m 86 161 (第二时段)9：009：10 7n m n 99 合计 30 185 （1）根据表格信息，在表格中填写第一时段电瓶车和货车的数量。 （2）在第二时段内，电瓶车和公交车的车辆数之和恰好是第二时段车流总量的一半，且两个时段的电瓶 车总数为 170 辆。 求 m，n 的值。 因为第二时段内车流总量较多，造成了交通拥堵现象，据估计，该时段内，每增加 1 辆公交车，可减少 8 辆小轿车和 5 辆电瓶年，若要使得第二时段和第一时段的车流
10、总量最接近，则应增加几辆公交车？ 24.如图，在平面直角坐标系中，直线 y= x+15 分别交 x 轴、y 轴于点 A，B，交直线 y= x 于点 M。动 点 C 在直线 AB 上以每秒 3 个单位的速度从点 A 向终点 B 运动，同时，动点 D 以每秒 a 个单位的速度从点 0 沿 OA 的方向运动，当点 C 到达终点 B 时，点 D 同时停止运动.设运动时间为 t 秒。 （1）求点 A 的坐标和 AM 的长。 （2）当 t=5 时，线段 CD 交 OM 于点 P，且 PC=PD，求 a 的值。 （3）在点 C 的整个运动过程中， 直接用含 t 的代数式表示点 C 的坐标。 利用(2)的结论
11、，以 C 为直角顶点作等腰直角 CDE(点 C，D，E 按逆时针顺序排列)。当 OM 与 CDE 的 一边平行时，求所有满足条件的 t 的值。 答案解析答案解析 一、选择题(本题有 10 小题，每小题 4 分，共 40 分.) 1.【答案】 A 【考点】相反数及有理数的相反数 【解析】【解答】解：-5 的相反数是 5 故答案为：A 【分析】根据求一个数的相反数就是在这个数的前面添上“-”号，再化简就可求出结果。 2.【答案】 B 【考点】科学记数法表示绝对值较大的数 【解析】【解答】解：42000=4.2104. 故答案为：B. 【分析】根据科学记数法的表示形式为：a10n。其中 1|a|10
12、，此题是绝对值较大的数，因此 n=整数 数位-1。 3.【答案】 C 【考点】简单组合体的三视图 【解析】【解答】解：从正面看，有一个长方形的上面是一个圆，长方形的长大于圆的直径， 故答案为：C. 【分析】主视图就是从几何体的正面所看到的平面图形，观察几何体可得答案。 4.【答案】 A 【考点】概率公式 【解析】 【解答】 解： 从装有 2 个黄球、 3 个红球和 5 个白球的袋中任意摸出一个球有 10 种等可能结果， 其中摸出的球是白球的结果有 5 种， 从袋中任意摸出一个球，是白球的概率是 = ， 故选：A 【分析】由题意可得，共有 10 可能的结果，其中从口袋中任意摸出一个球是白球的有
13、5 情况，利用概率 公式即可求得答案此题考查了概率公式，明确概率的意义是解答问题的关键，用到的知识点为：概率= 所求情况数与总情况数之比 5.【答案】 B 【考点】一元二次方程根的判别式及应用 【解析】【解答】解：关于 x 的一元二次方程 4x-4x+c=0 有两个相等实数根， b2-4ac=0，即 16-16c=0 解之：c=1. 故答案为：B. 【分析】由已知一元二次方程有两个相等的实数根，可得到 b2-4ac=0，由此建立关于 c 的方程，解方程求 出 c 的值。 6.【答案】 D 【考点】解一元一次不等式组 【解析】【解答】解： * 由得：x4 由得：x1 此不等式组的解集为：x4.
14、故答案为：D. 【分析】分别求出不等式组中的每一个不等式的解集，再利用大大取大，可得不等式组的解集。 7.【答案】 C 【考点】解直角三角形 【解析】【解答】解：在 Rt ADC 中，ACD=，AC=2.8， AD=ACsinACD=2.8sin= . 故答案为：C. 【分析】在 Rt ADC 中，利用锐角三角函数的定义可求出 AD 的值。 8.【答案】 D 【考点】二次函数的实际应用-几何问题 【解析】【解答】解：由题意得 故答案为：D. 【分析】由题意可知矩形的长+2 宽=52，用含 x 的代数式表示出矩形的宽，再利用矩形的面积公式就可求 出 y 与 x 的函数解析式。 9.【答案】 C
15、【考点】反比例函数的性质 【解析】【解答】解： 反比例函数 y= (k0)，当-2x-1 时，y 的最大值是 3， 此函数图像分支在第二、四象限 当 x=-1 时，y 的最大值为 3 k=-13=-3. 当 x6 时 y 有最小值为 . 故答案为：C. 【分析】由已知反比例函数 y= (k0)，当-2x-1 时，y 的最大值是 3，就可得到反比例函数的图像所在 的象限，由此可得到当 x=-1 时，y 的最大值为 3，据此可得到函数解析式，再由 x 的取值范围可得到 y 的 最值。 10.【答案】 D 【考点】正多边形和圆 【解析】【解答】解：设正六边形 ABCDEF 的外接圆的圆心为 O，连接
16、 AE，AD，OG， OG 平分弧 CD，正六边形 ABCD， AOF=60，DOG=COG=30， DAG= DOG=15 AOF=HPA+DAG HPA=60-15=45， HAP 是等腰直角三角形， HPA=45， AH=APsinHPA= 在 Rt AOH 中，AOH=60 即 解之：AO=OC=4. 弧 CG 的长为 . 故答案为：D 【分析】设正六边形 ABCDEF 的外接圆的圆心为 O，连接 AE，AD，OG，利用正多边形的性质和圆周角定 理可求出DAG，AOF 的度数，同时可得到DOG=COG=30，HPA=45，再利用解直角三角形求出 AH 的长，继而可求出 OA 的长，然后
17、利用弧长公式进行计算可求出弧 CG 的长。 二、填空题(本题有 6 小题，每小题 5 分，共 30 分) 11.【答案】 m（m-2） 【考点】因式分解运用公式法 【解析】【解答】解：m2-2m=m（m-2）. 故答案为：m（m-2）. 【分析】观察此多项式的特点：含有公因式 a，由此利用提取公因式法分解因式。 12.【答案】 5 【考点】平均数及其计算，中位数 【解析】【解答】解：一组数据 1，2，x，5，8 的平均数是 5 1+2+x+5+8=55 解之：x=9 排序为：1，2，5，8，9，最中间的数,5 这组数据的中位数是 5. 故答案为：5. 【分析】利用平均数公式求出 x 的值，再将
18、 5 个数从小到大排列，然后利用中位数的定义可求出这组数 据的中位数。 13.【答案】 x+1 【考点】分式的加减法 【解析】【解答】解：原式= ( )( ) . 故答案为：x+1. 【分析】将原式转化为同分母，再利用同分母分式的减法法则进行计算，然后将结果化成最简分式。 14.【答案】 70 【考点】圆周角定理，切线的性质 【解析】【解答】解：连接 OA，OB， PA，PB 是圆 O 的切线， OAP=PBO=90， 弧 AB=弧 AB AOB=2ACB=255=110 APB=360-PAO-PBO-AOB=360-90-90-110=70. 故答案为：70. 【分析】 连接 OA， OB
19、， 利用切线的性质求出PAO 和PBO 的度数， 利用圆周角定理求出AOB 的度数， 然后利用四边形的内角和定理求出APB 的度数。 15.【答案】 【考点】正方形的性质 【解析】【解答】解：过点 B 作 BMAE 于点 M，过点 C 作 CHAG 于点 H, 正方形 ABED，正方形 ACGF， AM=EM=BM，AH=HG=CH 设 BM=x，CH=y 2x+2y= ， 在 Rt ABC 中， AB2+CA2=BC2 2x2+2y2=49 ) ( ) 解之：xy= S ABC= 故答案为： 【分析】 过点 B 作 BMAE 于点 M，过点 C 作 CHAG 于点 H，利用正方形的性质，可证
20、得 AM=EM=BM， AH=HG=CH，设 BM=x，CH=y，求出 x+y 的值，利用勾股定理用含 x，y 的代数式分别表示出 AB，CA，再利 用勾股定理求出 2x2+2y2=49，由此可求出 xy 的值，然后利用三角形的面积公式可求解。 16.【答案】 40 ； 【考点】平行线分线段成比例，解直角三角形的应用 【解析】【解答】解：EF 比 CD 长 1mm EF=CD+1 由题意知 OF=OD， 设 OE=x，则 OC=x+1， 在 Rt COE 中 OE2+EC2=OC2 x2+92=（x+1）2 解之：x=40 OE=40； 延长 AB交 CE 于点 H， ABOF CBA=135
21、，CB= CBH=180-135=45， HB=CH=CBcosCBH= HE=EC-CH=9-2=7 设 CG=a，则 HG=2-a，GE=CE-CG=9-a 解之： 故答案为：40， 【分析】由题意可知 OF=OD，EF=CD+1，设 OE=x，则 OC=x+1，在 Rt COE 中，利用勾股定理建立关于 x 的方程，解方程求出x的值，即可得到OE的长；延长AB交CE于点H，利用平行线分线段成比例可 得出 ；再由CBA=135，CB的长，可求出 CBH 是等腰直角三角形，利用解直角三角形求出 HB，CH 的长及 HE 的长，再 CG=x，用含 x 的代数式表示出 HG，GE 的长，据此可建
22、立关于 a 的方程，解 方程求出 a 的值即可。 三、解答题(本题有 8 小题，共 80 分.) 17.【答案】 （1）原式= ； （2）原式=4a2+4a+1-4a2+4a=8a+1 【考点】实数的运算，整式的混合运算 【解析】【分析】（1）先算乘方和开方运算，同时化简绝对值，再合并即可。 （2）利用完全平方公式和单项式乘以多项式的法则，先去括号，再合并同类项。 18.【答案】 （1）证明：BD 平分ABC， EBC=ABE， CEBD， CEB=A=90， 在 CEB 和 DAB 中， ) ABDEBC（AAS）. （2）解： ABDEBC ADB=BCE=60 EBC=90-BCE=90
23、-60=30， BD=BC， BDC=BCD=（180-EBC）2=（180-30）2=75， DCE=DCB-ECB=75-60=15. 【考点】全等三角形的判定与性质，等腰三角形的性质 【解析】【分析】（1）利用角平分线的定义和垂直的定义可证得EBC=ABE，CEB=A，再利用 AAS 证明 ABDEBC。 （2）利用全等三角形的性质，可证得ADB=BCE，就可求出EBC 的度数，再利用等边对等角及三角形 内角和定理求出BDC 的度数，然后根据DCE=DCB-ECB，代入计算求出DCE 的度数。 19.【答案】 （1）本次抽样调查的书籍有 820=40 本； （2）由题意得： 其它类的书籍
24、有 40-8-10-16=6 本. （3）由题意得： 答：估计有 400 本科普类书籍。 【考点】用样本估计总体，扇形统计图，条形统计图 【解析】【分析】（1）本次抽样调查的书籍的数量=捐艺术类的书籍的数量捐艺术类的书籍的数量所占 的百分比，列式计算可求解。 （2）用 360捐文学类书籍的数量所占的百分比。列式计算可求解；再求出其它类的数据的数量，然后补 全条形统计图。 （3）用师生一共捐书的总数捐科普类书籍数量的百分比。然后列式计算可求解。 20.【答案】 （1）如图 （2）如图 【考点】平行四边形的判定，作图复杂作图 【解析】【分析】（1）利用等腰三角形的定义，画出以 AB 为腰的格点等腰
25、 ABC 即可。 （2）利用平行四边形的判定方法，画出以 AB 为边，且一个内角为 45的平行四边形 ABCD。 21.【答案】 （1）解： 抛物线的对称轴为直线 x= 解之：b=3 抛物线的解析式为 y=-x2+3x+4= ( ) . 点 M( ， ) （2）略 【考点】二次函数图象的几何变换，二次函数与一次函数的综合应用 【解析】【解答】（2）设对称轴交 AB 于点 H，交 OA 于点 N, 当 x=0 时 y=4 点 B（0，4） ABy 轴， 点 H( ， ) m= ； 当 y=4 时，-x2+3x+4=4 解之：x1=0，x2=3 点 A（3，4） 设直线 OA 的解析式为 y=kx
26、 3k=4 解之： 当 时 点 （ ， ） m= m 的取值范围是： . 故答案为： . 【分析】（1）利用抛物线的对称轴公式求出 b 的值，即可得到函数解析式，再将函数解析式转化为顶点 式，就可得到点 M 的坐标。 （2）设对称轴交 AB 于点 H，交 OA 于点 N，利用函数解析式求出点 B 的坐标即可得到点 H 的坐标，利用 平移的性质可求出 m 的值；由 y=4 可得到 x 的值，由此可得到点 A 的坐标，再利用待定系数法求出直线 OA 的函数解析式，利用函数解析式求出点 N 的坐标，利用点的坐标平移的性质求出 m 的值，综上所述可 得到 m 的取值范围。 22.【答案】 （1）证明：
27、AD 是直径，CEAD AD 垂直平分 CE，弧 AE=弧 AC， EF=CF，DE=CD，EDF=FDC， CFDE， EDF=DFC， FDC=DFC， CF=CD CF=CD=DE=EF 四边形 DCFE 是菱形. （2）解：四边形 DCFE 是菱形。 EFCD， AEF=B， tanAEF=tanB= ， AD 是直径， AED=BED=ACD=90， , 设 DE=DC=3x，BE=4x， BD=5x， BC=BD+CD 解之： CD= . 在 Rt ACD 中 圆的直径为 . 【考点】圆的综合题 【解析】【分析】（1）利用垂径定理可证明 AD 垂直平分 CE，弧 AE=弧 AC，利
28、用垂直平分线的性质及圆 周角定理可得到 EF=CF，DE=CD，EDF=FDC，再证明 CF=CD，然后利用菱形的判定定理可证得结论。 （2）利用菱形的性质及平行线的性质，可证得AEF=B，利用解直角三角形求出 BC 的长，利用圆周角 定理可得到AED=BED=ACD=90， 从而可求出 DE 与 BE 的比值， 设 DE=DC=3x， BE=4x， 可得到 BD=5x， 利用 BC 的长建立关于 x 的方程，解方程求出 x 的值，继而可求出 CD 的长，然后利用勾股定理求出 AD 的 长。 23.【答案】 （1）解：第一时段货车的数量为：30-n 第一时段电瓶车的数量为：161-m-86-（
29、30-n）=45-m+n； （2）解：由题意得： ) 解之： ) 设第二时段应增加 x 辆公交车，第二时段的车流量为 y 辆， y=716+3+16+99+x-（8+5）x=-12x+230， 当 y=161 时，-12x+230=161 解之： 应该增加 6 辆公交车. 【考点】一次函数与二元一次方程（组）的综合应用 【解析】【分析】（1）根据表中的数据可得到第一时段货车的数量；第一时段电瓶车的数量。 （2）此题的等量关系为：第二时段内，电瓶车的辆数+公交车的车辆数=第二时段车流总量的一半，且 两个时段的电瓶车总数为 170 辆，设未知数，列方程组，求出方程组的解即可；设第二时段应增加 x
30、辆公交车，第二时段的车流量为 y 辆，根据题意列出 y 与 x 的关系式，根据若要使得第二时段和第一时段 的车流总量最接近，求出 y=161 时，x 的值，即可得到结果。 24.【答案】 （1）解：当 y=0 时， 解之：x=20 点 A（20，0）； 两直线相交于点 M ) 解之： ) 点 M（12，6） 过点 M 作 MGOA 于点 G OG=12，MG=6 AG=20-12=8 在 Rt AMG 中， ; （2）解：动点 C 在直线 AB 上以每秒 3 个单位的速度从点 A 向终点 B 运动，同时，动点 D 以每秒 a 个单 位的速度从点 0 沿 OA 的方向运动， 当 t=5 时则 A
31、C=15，OD=5a，AB=25 点 C（8，9） 过点 C 作 CQx 轴交 OM 的延长线于点 Q， 点 Q（18，9） CQ=18-8=10， CQx 轴 G=DOP 在 CPQ 和 DPO 中， ) CPQDPO（AAS） CQ=OD 即 5a=10 解之：a=2. （3）解：过点 C 作 CKx 轴于点 K， 由题意可知 AC=3t，AB=25，OB=15， CKy 轴， ACKABO 即 解之： 当 时，则 解之： 点 ( ， ); 由可知 CK= ， OK= AC=3t，OD=2t，tanMOA= 当 CDOM 时， 即 解之：t= ； 当 CEOM 时， ECD=CPO=90
32、DCK+CDK=DOP+CDK=90 DCK=DOP tanDCK= CK=2DK DK=OD-OK= ( ) ( ) 解之： ; 当 DEOM 时，过点 E 作 EHx 轴于点 H，过点 C 作 CKx 轴于点 K，过点 C 作 CGx 轴交 HE 于点 G， 等腰直角 CDE CD=CE 易证 CDKCEG， CK=CG=GH= ， , ( ) , , OMED， MOA=EDH， DH=2EH ( ) 解之：t=4. t 的值为 或 或 4. 【考点】相似三角形的判定与性质，与一次函数有关的动态几何问题 【解析】【分析】（1）由 y=0 求出对应的 x 的值，从而可得到点 A 的坐标，再
33、将两函数解析式联立方程 组，解方程组求出 x，y 的值，就可得到点 M 的坐标，过点 M 作 MGOA 于点 G，由此可求出 OG，MG， AG 的长，然后在 Rt AMG 中，利用勾股定理求出 AM 的长。 （2）由 t 的值，可得到 AC 的长，同时可得到 OD，利用勾股定理求出 AB 的长，利用相似三角形的判定和 性质可求出点 C 的坐标，过点 C 作 CQx 轴交 OM 的延长线于点 Q，可求出点 Q 的坐标，继而可得到 CQ 的长，利用平行线的性质，可证得G=DOP，再利用 AAS 证明 CPQDPO，利用全等三角形的性质， 可知 CQ=OD，据此建立关于 a 的方程，解方程求出 a
34、 的值。 （3） 过点 C 作 CKx 轴于点 K，由题意可知 AC=3t，AB=25，OB=15， ， 利用平行可证得 ACKABO， 利用相似三角形的性质，可用含 t 的代数式表示出 CK，将 x=CK 代入函数解析式求出对应的函数值，即可 得到点 C 的坐标；由可知 CK，OK 的长，同时可得到 AC=3t，OD=2t，tanMOA= ，再分情况讨论： 当 CDOM 时，利用平行线分线段成比例建立关于 t 的方程，解方程求出 t 的值；当 CEOM 时，先证明 DCK=DOP，再利用锐角三角函数的定义可证得 CK=2DK，代入建立关于 t 的方程，解方程求出 t 的值； 当 DEOM 时，过点 E 作 EHx 轴于点 H，过点 C 作 CKx 轴于点 K，过点 C 作 CGx 轴交 HE 于点 G， 易证 CDKCEG，利用全等三角形的性质，分别用含 t 的代数式表示出 CK，GE，EH。DH 的长，再证明 MOA=EDH，利用锐角三角函数的定义可得到 DH=2EH，据此建立关于 t 的方程，解方程求出 t 的值。 综上所述可得满足条件的 t 的值。
