1、20202020 年初中学业水平考试适应性测试年初中学业水平考试适应性测试数学试数学试卷卷 考生须知： 1 本试卷满分 120 分，考试时间为 120 分钟. 2 答题前，考生先将自己的“姓名” 、 “考号” 、 “考场” 、 “座位号”在答题卡上填写清楚，将“条形码”准 确粘贴在条形码区域内. 3 请按照题号顺序在答题卡各题目的区域内作答，超出答题区域的答案无效；在草稿纸上、试题纸上答案 无效. 4 选择题必须使用 2B 铅笔填涂；非选择题必须使用 0.5 毫米黑色字迹的签字笔书写，字体工整、笔迹清 楚. 5 保持卡面整洁，不要折叠、不要弄脏、弄皱，不准使用涂改液、刮纸刀. 试题卷试题卷 I
2、 I 一一. . 选择题选择题( (每小题每小题 4 4 分，共分，共 4040 分，在每小题给出的四个选项中，只有一项符合题目要求分，在每小题给出的四个选项中，只有一项符合题目要求) ) 1. 在0, 3,2, 1这四个数中，最大的数是（ ） A0 B3 C 2 D1 2. 下列运算正确的是（ ） A 224 2xxx B 325 x xx C 933 xxx D 3 25 xx 3.据交通运输部统计，受肺炎疫情影响，今年春运 1 月 25 日2 月 14 日，全国共发送旅客2.83亿人次，日 均1348万人次，同比分别下降82. 3%.将1348万用科学记数法表示为（ ） A 4 1348
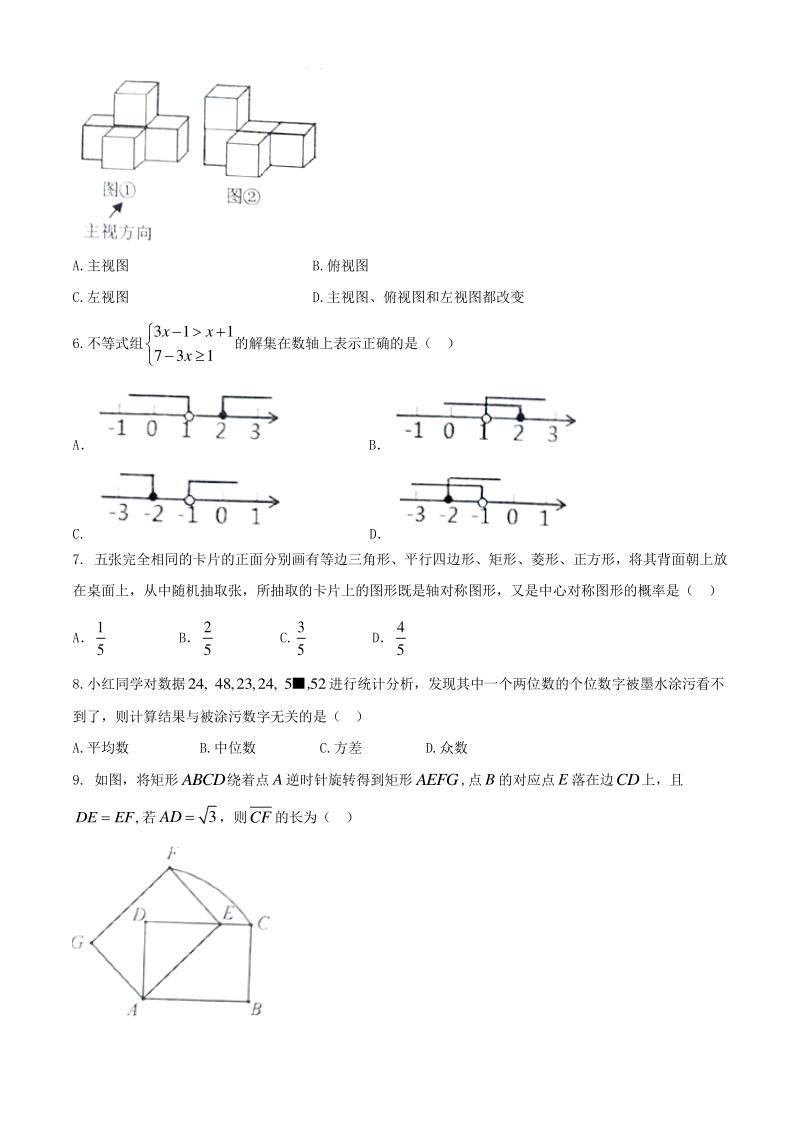
3、 10 B 6 13.48 10 C 6 1.348 10 D 7 1.348 10 4. 在函数 3 x y x 中，自变量x的取值范围是（ ） A3x B30xx且 C. 0x D3x 5.图是由五个完全相同的小正方体组成的立体图形，将图中的一个小正方体改变位置后如图，则三 视图发生改变的是（ ） A.主视图 B.俯视图 C.左视图 D.主视图、俯视图和左视图都改变 6.不等式组 311 731 xx x 的解集在数轴上表示正确的是（ ） A B C. D 7. 五张完全相同的卡片的正面分别画有等边三角形、平行四边形、矩形、菱形、正方形，将其背面朝上放 在桌面上，从中随机抽取张，所抽取的卡
4、片上的图形既是轴对称图形，又是中心对称图形的概率是（ ） A 1 5 B 2 5 C. 3 5 D 4 5 8.小红同学对数据24, 48,23,24, 552,进行统计分析，发现其中一个两位数的个位数字被墨水涂污看不 到了，则计算结果与被涂污数字无关的是（ ） A.平均数 B.中位数 C.方差 D.众数 9. 如图，将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上，且 ,DEEF若3AD ，则CF的长为（ ） A 3 8 B 3 4 C. 6 4 D 10. 在矩形ABCD内，将两张边长分别为a和bab的正方形纸片按图 1,图 2 两种方式放置(图 1,图 2 中
5、两张正方形纸片均有部分重叠)，矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图 2 中阴影部 分的周长与图 1 中阴影部分的周长的差为1,若要知道l的值,只要测量图中哪条线段的长（ ） Aa Bb C.AD DAB 试题卷试题卷 IIII 二、填空题二、填空题: :（每题（每题 5 5 分，共分，共 3030 分）分） 11.分解因式： 22 4xy 12.64的立方根是 13. 已知圆锥的母线和高线的长是一元二次方程 2 8150xx的两个根， 则圆锥的侧面积为 14. 在一次综合社会实践活动中，小东同学从A处出发，要到A地北偏东60方向的C处，他先沿正东方 向走了4干米到达B处， 再沿
6、北偏东15方向走， 恰能到达目的地C,如图所示， 则,A C两地相距 千 米，(结果精确到0.1千米，参考数据:21.414, 31.732) 15.如图，在矩形ABCD中，3, 4, ABBCP是对角线AC上的动点，以点P为圆心，PC长为半径 作OP.当OP与矩形ABCD的边相切时，CP的长为 16. 如图，在平面直角坐标系中，OAB的边OB在x轴的正半轴上，, AOAB M是边AB的中点，经 过点M的反比例函数0,0 k ykx x 的图象与边OA交于点C,则 OC OA 的值为 三三. . 解答题解答题( (本大题有本大题有 8 8 小题，共小题，共 8080 分分) ) 17. 1计算
7、： 30 239 2解方程： 23 1 33 x xx 18.图 1,图 2 都是由边长为1的小等边三角形构成的网格，ABC为格点三角形，请仅用无刻度直尺在网格 中完成下列画图. 1在图 1 中，画出ABC中AB边上的中线CM: 2在图 2 中，画出APC,使APCABC,且点P是格点(画出一个即可). 19.某校为了解学生对 “防溺水” 安全知识的掌握情况， 从全校1500名学生中随机抽取部分学生进行测试， 并将测试成绩(百分制，得分均为整数)进行统计分析，绘制了如下不完整的频数表和频数直方图. 被抽取的部分学生安全知识测试成绩频数表 组别 成绩（分） 频数（人） 频率 A组 5060x 6
8、 0.12 B组 6070x a 0.28 C组 7080x 16 0.32 D组 8090x 10 0.20 E组 90100x 4 0.08 由图表中给出的信息回答下列问题: 1表中的a ;抽取部分学生的成绩的中位数在 组; 2把上面的频数直方图补充完整; 3如果成绩达到80分以上(包括80分)为优秀，请估计该校1500名学生中成绩优秀的人数. 20.如图，已知二次函数 2 yxbxc 的图象经过点3,1A,点0,4B 1求该二次函数的表达式及顶点坐标: 2点, C m n在该二次函数图象上. 当1m时，求n的值: 当3mx时，n最大值为5,最小值为1,请根据图象直接写出m的取值范围. 2
9、1.如图，在ABCD中。对角线,AC BD相交于点O，过点O作BD的要线与 边,AD BC分别交于点,E F连接BE交AC于点K,连接DF 1求证:四边形EBFD是菱形; 2若3, 4,BKEK AE求四边形EBFD的周长. 22.小明星期天上午8:00从家出发到离家36千米的书城买书，他先从家出发骑公共自行车到公交车站，等 了12分钟的车，然后乘公交车于9:48分到达书城(假设在整个过程中小明骑车的速度不变，公交车匀速行 驶，小明家、公交车站、书城依次在一条笔直的公路旁).如图是小明从家出发离公交车站的路程 y(千米) 与他从家出发的时间x(时)之间的函数图象，其中线段AB对应的函数表达式为
10、6.ykx 1求小明骑公共自行车的速度: 2求线段CD对应的函数表达式; 3求出发时间x在什么范围时，小明离公交车站的路程不超过3千米? 23.如图 1,平面内有一点P到ABC的三个顶点的距离分别为,PAPBPC、若有 222 PAPBPC，则 称点P为ABC关于点C的勾股点。 1如图 2,在4 3的方格纸中， 每个小正方形的边长均为1, ABC的顶点在格点上， 请找出所有的格点P， 使点P为ABC关于点A的勾股点. 2如图 3, ABC为等腰直角三角形，P是斜边BC延长线上一点，连接AP,以AP为直角边作等腰直 角三角形 APD(点A PD、 、顺时针排列)，90PAD ,连接 , ,DC
11、DB 求证:点P为BDC关于点D的勾股点. 3如图 4,点E是矩形ABCD外一点， 且点C是ABE关于点A的勾股点， 若8,5,ADCEADDE, 求AE的长， 24.如图 1,直线 1 :4 2 l yx 与x轴交于点A,与y轴交于点B,以AB为直径作OM，点P为线段OA 上一动点(与点,O A不重合)，作PCAB于C,连结BP并延长交O于点D 1求点,A B的坐标和tan BAO的值: 2设,tan BC xBPOy CA 当1x 时，求y的值及点D的坐标: 求y关于x的函数表达式: 3如图 2,连接OC,当点P在线段OA上运动时，求OC PD的最大值. 2020 年初中学业水平考试参考答
12、案与评分标准年初中学业水平考试参考答案与评分标准 数数 学学 一、选择题一、选择题:(:(每小题每小题 4 4 分，共计分，共计 4 40 0 分分) ) 1-5:CBDDA 6-10:BCBBD 二、二、填空题（每小题填空题（每小题 5 5 分，共分，共 30 30 分）分） 11.22xyxy 12.4 13.20 14. 5.5 15.15 20 89 或 16. 3 2 三、解答题（本大题有三、解答题（本大题有 8 8 小题，共小题，共 80 80 分）分） 注注: 1.: 1.阅卷时应按步计分，每步只设整分阅卷时应按步计分，每步只设整分; ; 2.2.如有其它解法，只要正确，都可参照
13、评分标准，各步相应给分如有其它解法，只要正确，都可参照评分标准，各步相应给分. . 17. 解： 1原式8 3 3 1 7 ； 2方程的两边同乘 3x， 得233xx 即：253x ， 解得：1x 经检验1x 是原方程的解 18. 解： 1如图 1 所示，CM即为ABC中AB边上的中线； 2如图 2 所示，APC即为所求的角(画出一个即可) 19.解： 1 14;C 2补全频数直方图如下： 3估计该校1500名学生中成绩优秀的人数为 14 1500420 50 （人） 20.解： 1把点3,1A，点0,4C代入二次函数 2 yxbxc 得 931 4 bc c 解得 2 4 b c 二次函数表
14、达式为 2 24yxx 2 2 2415yxxx 顶点坐标为1,5 2当1m时， 2 12141n 11m 21. 1 证明：四边形ABCD是平行四边形， /ADBCOA OCODOB， EAOFCOOEAOFC， OEAOFC， OEOF， 四边形EBFD是平行四边形， EFBD， 四边形EBFD是菱形 2解：OEAOFC = 4 CFAE， / 3ADBC BKEK， EAKBCKAEKCBK， EAKBCK AEEK BCBK 即 41 13BF 8BF ， 四边形EBFD的周长为4 832 22.解： 16ykx 当0x时， 6y ， 小明骑公共自行车的速度为 6 10 0.6 （千米
15、/小时） 12 20.2 60 ，36 630a ， 48 11.8 60 b 点0.8,0C， 点1.8,30D 设线段CD对应的函数表达式为ymxb 则 00.8 301.8 mb mb 解得 30 24 m b 线段CD对应的函数表达式为3024yx 3把0.6,0B代入6ykx 得10k ， 即 106yx ， 当3y 时， 3106x 解得0.3x 当3y 时， 33024x 解得0.9x 由图象可知，当0.30.9hxh时，小明离车站的路程不超过3千米 23.解： 1如图，点 12 ,P P即为所求的点 2证明：由题意9045ABACADAPBACDAPABCACB ， BACDA
16、CDAPDAC 即BADCAP， BADCAP， 135 ABDACPPCDB ， 1354590CBDABDABC ， 222 DBPBPD 222 PDPBPD 点P为BDC关于点D的勾股点 3如图，作EMAD于点M，交BC于点N 四边形ABCD为矩形， /BCAD， ENBC， 点C是ABE关于点A的勾股点， 222 CBCECA 22 5CECACBABCD 设ENx ， 由题意，可得四边形MNCD为矩形， 5MNCDNCMD， 8ADDE ， 222 5NCx， 2 22 85MDx 2 222 585xx 解得 7 5 x 2 2 724 85 55 MD 2416 8 55 AM
17、， 732 55 55 EMx 22 22 163216 5 555 AEAMEM 24.解： 1 1:4 2 l yx ， 当0x时，4y 当0y 时，8x ,8,04 ,0,AB 4,8,90OBOAAOB 1 2 OB tan BAO OA 2当 1x 时，点C与M重合， 即CACB，如图 1 PCAB， PAPB， 设OPa ，则8PBPAa ， 在Rt BOP中， 2 22 48aa 解得3a 4 3 OB ytan BPO OP 如图 1，连接AD， 作DHOA于H AB是M的直径 90ADB 4 5 3 APtan APDtan BPO， 34PDAD， 3 412 55 DH
18、， 2 2 129 3 55 PH 924 3 55 OH 点D的坐标为 2412 , 55 如图 2，作BEAB交x轴于点E 90OBEBAOABO ， 1 2 tan OBEtan BAO 2OEOB tan OBE ， PCAB， /PCBE， EPBC x PACA 即 2 8 OP x OP 82 1 x OP x 22 41 BOx tan BPO OPx y关于x的函数表达式为 22 41 x y x 3如图 3，连接OD 由题意，90ACPAOBCAPOAB ， CAPOAB， APAC ABAO APBACO AOCABPDOP CAOD ， OCAOPD OCAC OPPD 设PAt，则 2 5 ACt 2 22 516 5 8 555 OC PDOP ACtttt 22 532 5 4 55 t 当4t 时，OC PD的最大值为 32 5 5
