1、备战备战 2020 高考物理高考物理专题专题 01 运动的描述、匀变速直线运动运动的描述、匀变速直线运动 第一节第一节 描述运动的基本概念描述运动的基本概念 【基本概念、规律】【基本概念、规律】 一、质点、参考系 1质点：用来代替物体的有质量的点它是一种理想化模型 2参考系：为了研究物体的运动而选定用来作为参考的物体参考系可以任意选 取通常以地面或相对于地面不动的物体为参考系来研究物体的运动 二、位移和速度 1位移和路程 (1)位移：描述物体位置的变化，用从初位置指向末位置的有向线段表示，是矢量 (2)路程是物体运动路径的长度，是标量 2速度 (1)平均速度： 在变速运动中， 物体在某段时间内
2、的位移与发生这段位移所用时间的 比值，即 v x t，是矢量 (2)瞬时速度：运动物体在某一时刻(或某一位置)的速度，是矢量 3速率和平均速率 (1)速率：瞬时速度的大小，是标量 (2)平均速率：路程与时间的比值，不一定等于平均速度的大小 三、加速度 1定义式：av t；单位是 m/s 2. 2物理意义：描述速度变化的快慢 3方向：与速度变化的方向相同 【重要考点归纳总结】【重要考点归纳总结】 考点一考点一 对质点模型的理解对质点模型的理解 1质点是一种理想化的物理模型，实际并不存在 2 物体能否被看做质点是由所研究问题的性质决定的， 并非依据物体自身大小来判断 3物体可被看做质点主要有三种情
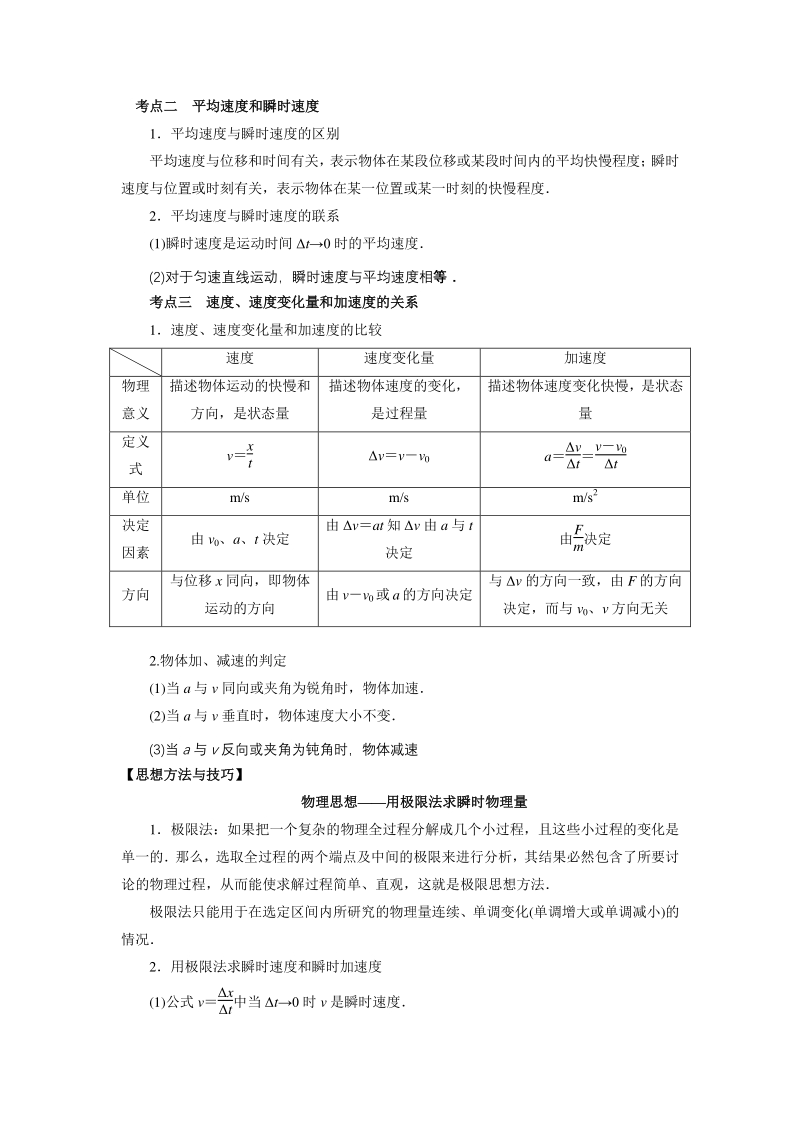
3、况： (1)多数情况下，平动的物体可看做质点 (2)当问题所涉及的空间位移远大于物体本身的大小时，可以看做质点 (3)有转动但转动可以忽略时，可把物体看做质点 考点二考点二 平均速度和瞬时速度平均速度和瞬时速度 1平均速度与瞬时速度的区别 平均速度与位移和时间有关， 表示物体在某段位移或某段时间内的平均快慢程度； 瞬时 速度与位置或时刻有关，表示物体在某一位置或某一时刻的快慢程度 2平均速度与瞬时速度的联系 (1)瞬时速度是运动时间 t0 时的平均速度 (2)对于匀速直线运动，瞬时速度与平均速度相等 考点三考点三 速度、速度变化量和加速度的关系速度、速度变化量和加速度的关系 1速度、速度变化量
4、和加速度的比较 速度 速度变化量 加速度 物理 意义 描述物体运动的快慢和 方向，是状态量 描述物体速度的变化， 是过程量 描述物体速度变化快慢，是状态 量 定义 式 vx t vvv0 av t vv0 t 单位 m/s m/s m/s2 决定 因素 由 v0、a、t 决定 由 vat 知 v 由 a 与 t 决定 由F m决定 方向 与位移 x 同向，即物体 运动的方向 由vv0或a的方向决定 与 v 的方向一致，由 F 的方向 决定，而与 v0、v 方向无关 2.物体加、减速的判定 (1)当 a 与 v 同向或夹角为锐角时，物体加速 (2)当 a 与 v 垂直时，物体速度大小不变 (3)
5、当a与v反向或夹角为钝角时，物体减速 【思想方法与技巧】【思想方法与技巧】 物理思想物理思想用极限法求瞬时物理量用极限法求瞬时物理量 1极限法：如果把一个复杂的物理全过程分解成几个小过程，且这些小过程的变化是 单一的那么，选取全过程的两个端点及中间的极限来进行分析，其结果必然包含了所要讨 论的物理过程，从而能使求解过程简单、直观，这就是极限思想方法 极限法只能用于在选定区间内所研究的物理量连续、单调变化(单调增大或单调减小)的 情况 2用极限法求瞬时速度和瞬时加速度 (1)公式 vx t中当 t0 时 v 是瞬时速度 (2)公式 av t中当 t0 时 a 是瞬时加速度 第二节第二节 匀变速直
6、线运动的规律及应用匀变速直线运动的规律及应用 【基本概念、规律】【基本概念、规律】 一、匀变速直线运动的基本规律 1速度与时间的关系式：vv0at. 2位移与时间的关系式：xv0t1 2at 2. 3位移与速度的关系式：v2v202ax. 二、匀变速直线运动的推论 1平均速度公式： v vt 2 v0v 2 . 2位移差公式：xx2x1x3x2xnxn1aT2. 可以推广到 xmxn(mn)aT2. 3初速度为零的匀加速直线运动比例式 (1)1T 末，2T 末，3T 末瞬时速度之比为： v1v2v3vn123n. (2)1T 内，2T 内，3T 内位移之比为： x1x2x3xn12232n2.
7、 (3)第一个 T 内，第二个 T 内，第三个 T 内位移之比为： xxxxn135(2n1) (4)通过连续相等的位移所用时间之比为： t1t2t3tn1( 21)( 3 2)( n n1) 三、自由落体运动和竖直上抛运动的规律 1自由落体运动规律 (1)速度公式：vgt. (2)位移公式：h1 2gt 2. (3)速度位移关系式：v22gh. 2竖直上抛运动规律 (1)速度公式：vv0gt. (2)位移公式：hv0t1 2gt 2. (3)速度位移关系式：v2v202gh. (4)上升的最大高度：hv 2 0 2g. (5)上升到最大高度用时：tv0 g. 【重要考点归纳】【重要考点归纳】
8、 考点一考点一 匀变速直线运动基本公式的应用匀变速直线运动基本公式的应用 1速度时间公式 vv0at、位移时间公式 xv0t1 2at 2、位移速度公式 v2v2 02ax， 是匀变速直线运动的三个基本公式，是解决匀变速直线运动的基石 2匀变速直线运动的基本公式均是矢量式，应用时要注意各物理量的符号，一般规定 初速度的方向为正方向，当 v00 时，一般以 a 的方向为正方向 3.求解匀变速直线运动的一般步骤 画过程 分析图 判断运 动性质 选取正 方向 选用公式 列方程 解方程 并讨论 4.应注意的问题 如果一个物体的运动包含几个阶段， 就要分段分析， 各段交接处的速度往往是联系各 段的纽带
9、对于刹车类问题，当车速度为零时，停止运动，其加速度也突变为零求解此类问题 应先判断车停下所用时间，再选择合适公式求解 物体先做匀减速直线运动， 速度减为零后又反向做匀加速直线运动， 全程加速度不变， 可以将全程看做匀减速直线运动，应用基本公式求解 考点二考点二 匀变速直线运动推论的应用匀变速直线运动推论的应用 1推论公式主要是指： v vt 2 v0vt 2 ，xaT2，式都是矢量式，在应用时 要注意 v0与 vt、x 与 a 的方向关系 2式常与 x v t 结合使用，而式中 T 表示等时间隔，而不是运动时间 考点三考点三 自由落体运动和竖直上抛运动自由落体运动和竖直上抛运动 1自由落体运动
10、为初速度为零、加速度为 g 的匀加速直线运动 2竖直上抛运动的重要特性 (1)对称性 时间对称 物体上升过程中从 AC 所用时间 tAC和下降过程中从 CA 所用时间 tCA 相等，同理 tABtBA. 速度对称 物体上升过程经过 A 点的速度与下降过程经过 A 点的速度大小相等 (2)多解性 当物体经过抛出点上方某个位置时，可能处于上升阶段，也可能处于下降阶段，造成双 解，在解决问题时要注意这个特点 3.竖直上抛运动的研究方法 分段法 下降过程：自由落体运动 全程法 将上升和下降过程统一看成是初速度 v0向上，加速度 g 向下的匀变速直线运动， vv0gt，hv0t1 2gt 2(向上为正)
11、 若 v0，物体上升，若 v0，物体在抛点上方，若 h0，物体在抛点下方 【思想方法与技巧】【思想方法与技巧】 物理思想物理思想用转换法求解多个物体的运动用转换法求解多个物体的运动 在涉及多体问题和不能视为质点的研究对象问题时， 应用“转化”的思想方法转换研究对 象、研究角度，就会使问题清晰、简捷通常主要涉及以下两种转化形式： (1)将多体转化为单体：研究多物体在时间或空间上重复同样运动问题时，可用一个物 体的运动取代多个物体的运动 (2)将线状物体的运动转化为质点运动：长度较大的物体在某些问题的研究中可转化为 质点的运动问题如求列车通过某个路标的时间，可转化为车尾(质点)通过与列车等长的位
12、移所经历的时间 第三节第三节 运动图象运动图象 追及、相遇问题追及、相遇问题 【基本概念、规律】【基本概念、规律】 一、匀变速直线运动的图象 1直线运动的 xt 图象 (1)物理意义：反映了物体做直线运动的位移随时间变化的规律 (2)斜率的意义： 图线上某点切线的斜率大小表示物体速度的大小， 斜率正负表示物 体速度的方向 2直线运动的 vt 图象 (1)物理意义：反映了物体做直线运动的速度随时间变化的规律 (2)斜率的意义： 图线上某点切线的斜率大小表示物体加速度的大小， 斜率正负表示 物体加速度的方向 (3)“面积”的意义 图线与时间轴围成的面积表示相应时间内的位移大小 若面积在时间轴的上方
13、，表示位移方向为正方向；若面积在时间轴的下方，表示 位移方向为负方向 二、追及和相遇问题 1两类追及问题 (1)若后者能追上前者，追上时，两者处于同一位置，且后者速度一定不小于前者速 度 (2)若追不上前者，则当后者速度与前者相等时，两者相距最近 2两类相遇问题 (1)同向运动的两物体追及即相遇 (2)相向运动的物体， 当各自发生的位移大小之和等于开始时两物体间的距离时即相 遇 【重要考点归纳】【重要考点归纳】 考点一考点一 运动图象的理解及应用运动图象的理解及应用 1对运动图象的理解 (1)无论是 xt 图象还是 vt 图象都只能描述直线运动 (2)xt 图象和 vt 图象都不表示物体运动的
14、轨迹 (3)xt 图象和 vt 图象的形状由 x 与 t、v 与 t 的函数关系决定 2应用运动图象解题“六看” xt 图象 vt 图象 轴 横轴为时间 t，纵轴为位移 x 横轴为时间 t，纵轴为速度 v 线 倾斜直线表示匀速直线运动 倾斜直线表示匀变速直线运动 斜率 表示速度 表示加速度 面积 无实际意义 图线和时间轴围成的面积表示位移 纵截距 表示初位置 表示初速度 特殊点 拐点表示从一种运动变为另一 种运动，交点表示相遇 拐点表示从一种运动变为另一种运 动，交点表示速度相等 考点二考点二 追及与相遇问题追及与相遇问题 1分析追及问题的方法技巧可概括为“一个临界条件”、“两个等量关系” (
15、1)一个临界条件：速度相等它往往是物体间能否追上或(两者)距离最大、最小的临界 条件，也是分析判断问题的切入点 (2)两个等量关系：时间关系和位移关系，通过画草图找出两物体的时间关系和位移关 系是解题的突破口 2能否追上的判断方法 (1)做匀速直线运动的物体 B 追赶从静止开始做匀加速直线运动的物体 A：开始时，两 个物体相距 x0.若 vAvB时， xAx0xB，则不能追上 (2)数学判别式法：设相遇时间为 t，根据条件列方程，得到关于 t 的一元二次方程，用 判别式进行讨论，若 0，即有两个解，说明可以相遇两次；若 0，说明刚好追上或相 遇；若 0，说明追不上或不能相遇 3注意三类追及相遇
16、情况 (1)若被追赶的物体做匀减速运动，一定要判断是运动中被追上还是停止运动后被追上 (2)若追赶者先做加速运动后做匀速运动，一定要判断是在加速过程中追上还是匀速过 程中追上 (3)判断是否追尾，是比较后面减速运动的物体与前面物体的速度相等的位置关系，而 不是比较减速到 0 时的位置关系 4.解题思路 分析物体 运动过程 画运动 示意图 找两物体 位移关系 列位移 方程 (2)解题技巧 紧抓“一图三式”，即：过程示意图，时间关系式、速度关系式和位移关系式 审题应抓住题目中的关键字眼，充分挖掘题目中的隐含条件，如“刚好”、“恰好”、“最 多”、“至少”等，它们往往对应一个临界状态，满足相应的临界
17、条件 【思想方法与技巧】【思想方法与技巧】 方法技巧方法技巧用图用图象法解决追及相遇问题象法解决追及相遇问题 (1)两个做匀减速直线运动物体的追及相遇问题，过程较为复杂如果两物体的加速度 没有给出具体的数值，并且两个加速度的大小也不相同，如果用公式法，运算量比较大，且 过程不够直观，若应用 vt 图象进行讨论，则会使问题简化 (2)根据物体在不同阶段的运动过程，利用图象的斜率、面积、交点等含义分别画出相 应图象，以便直观地得到结论 巧解直线运动六法巧解直线运动六法 在解决直线运动的某些问题时，如果用常规解法一般公式法，解答繁琐且易出错， 如果从另外角度入手，能够使问题得到快速、简捷解答.下面便
18、介绍几种处理直线运动的巧 法. 一、平均速度法 在匀变速直线运动中，物体在时间 t 内的平均速度等于物体在这段时间内的初速度 v0 与末速度 v 的平均值，也等于物体在 t 时间内中间时刻的瞬时速度，即 v x t v0v 2 vt 2. 如果将这两个推论加以利用，可以使某些问题的求解更为简捷 二、逐差法 匀变速直线运动中， 在连续相等的时间 T内的位移之差为一恒量， 即xxn1xnaT2， 一般的匀变速直线运动问题，若出现相等的时间间隔，应优先考虑用 xaT2求解 三、比例法 对于初速度为零的匀加速直线运动与末速度为零的匀减速直线运动， 可利用初速度为零 的匀加速直线运动的相关比例关系求解
19、四、逆向思维法 把运动过程的末态作为初态的反向研究问题的方法一般用于末态已知的情况 五、相对运动法 以系统中的一个物体为参考系研究另一个物体运动情况的方法 六、图象法 应用vt图象，可把较复杂的问题转变为较简单的数学问题解决尤其是用图象定性 分析，可避开繁杂的计算，快速找出答案 实验一实验一 研究匀变速直线运动研究匀变速直线运动 一、实验目的 1练习使用打点计时器， 学会用打上点的纸带研究物体的运动 情况 2会利用纸带求匀变速直线运动的速度、加速度 3利用打点纸带探究小车速度随时间变化的规律， 并能画出小 车运动的 vt 图象，根据图象求加速度 二、实验器材 电火花计时器(或电磁打点计时器)、
20、一端附有滑轮的长木板、 小车、纸带、细绳、钩码、刻度尺、导线、电源、复写纸片 三、实验步骤 1把附有滑轮的长木板放在实验桌上，并使滑轮伸出桌面，把打点计时器固定在长木 板上没有滑轮的一端，连接好电路 2把一条细绳拴在小车上，细绳跨过滑轮，下边挂上合适的钩码，把纸带穿过打点计 时器，并把它的一端固定在小车的后面实验装置见上图，放手后，看小车能否在木板上平 稳地加速滑行 3把小车停在靠近打点计时器处，先接通电源，后放开小车，让小车拖着纸带运动， 打点计时器就在纸带上打下一系列的点，换上新纸带，重复三次 4从几条纸带中选择一条比较理想的纸带，舍掉开始一些比较密集的点，在后面便于 测量的地方找一个开始
21、点，以后依次每五个点取一个计数点，确定好计数始点，并标明 0、 1、2、3、4、，测量各计数点到 0 点的距离 x，并记录填入表中. 位置编号 0 1 2 3 4 5 t/s x/m v/(m s 1) 5.计算出相邻的计数点之间的距离 x1、x2、x3、. 6利用一段时间内的平均速度等于这段时间中间时刻的瞬时速度求得各计数点 1、2、 3、4、5 的瞬时速度，填入上面的表格中 7增减所挂钩码数，再做两次实验 四、注意事项 1纸带、细绳要和长木板平行 2释放小车前，应使小车停在靠近打点计时器的位置 3实验时应先接通电源，后释放小车；实验后先断开电源，后取下纸带 一、数据处理 1匀变速直线运动的
22、判断： (1)沿直线运动的物体在连续相等时间 T 内的位移分别为 x1、x2、x3、x4、，若 xx2 x1x3x2x4x3则说明物体在做匀变速直线运动，且 xaT2. (2)利用“平均速度法”确定多个点的瞬时速度，作出物体运动的 vt 图象若 vt 图线 是一条倾斜的直线，则说明物体的速度随时间均匀变化，即做匀变速直线运动 2求速度的方法： 根据匀变速直线运动某段时间中间时刻的瞬时速度等于这段时间内的平均速度 vn xnxn1 2T . 3求加速度的两种方法： (1)逐差法：即根据 x4x1x5x2x6x33aT2(T 为相邻两计数点之间的时间间隔)， 求出 a1x4x1 3T2 ，a2x5
23、x2 3T2 ，a3x6x3 3T2 ，再算出 a1、a2、a3的平均值 aa1a2a3 3 1 3 x4x1 3T2 x5x2 3T2 x6x3 3T2 x4x5x6x1x2x3 9T2 ，即为物体的加速度 (2)图象法：以打某计数点时为计时起点，利用 vnxnxn 1 2T 求出打各点时的瞬时速度， 描点得 vt 图象，图象的斜率即为物体做匀变速直线运动的加速度 二、误差分析 1纸带上计数点间距测量有偶然误差，故要多测几组数据，以尽量减小误差 2纸带运动时摩擦不均匀，打点不稳定引起测量误差，所以安装时纸带、细绳要与长 木板平行，同时选择符合要求的交流电源的电压及频率 3用作图法作出的 vt 图象并不是一条直线为此在描点时最好用坐标纸，在纵、横 轴上选取合适的单位，用细铅笔认真描点 4在到达长木板末端前应让小车停止运动，防止钩码落地，小车与滑轮碰撞 5选择一条点迹清晰的纸带，舍弃点密集部分，适当选取计数点 6在坐标纸上，纵、横轴选取合适的单位(避免所描点过密或过疏，而导致误差过大)， 仔细描点连线，不能连成折线，应作一条平滑曲线，让各点尽量落到这条曲线上，落不到曲 线上的各点应均匀分布在曲线的两侧
