1、2020 年年 5 月中考数学模拟试卷月中考数学模拟试卷 一、选择题 15 的相反数是（ ） A B5 C5 D 2下列运算中正确的是（ ） A2a2 a3a3 B（ab2）2ab4 C2ab2b22a D（a+b）2a2+b2 3 新冠病毒平均直径为 0.0001 毫米， 但它以飞沫传播为主， 而飞沫的直径是大于 5 微米的， 所以 N95 或医用口罩能起到防护作用，用科学记数法表示 0.0001 毫米是（ ） A0.1105毫米 B104毫米 C103毫米 D0.1103毫米 4一个不等式的解集为1x2，那么在数轴上表示正确的是（ ） A B C D 5某露天舞台如图所示，它的俯视图是（
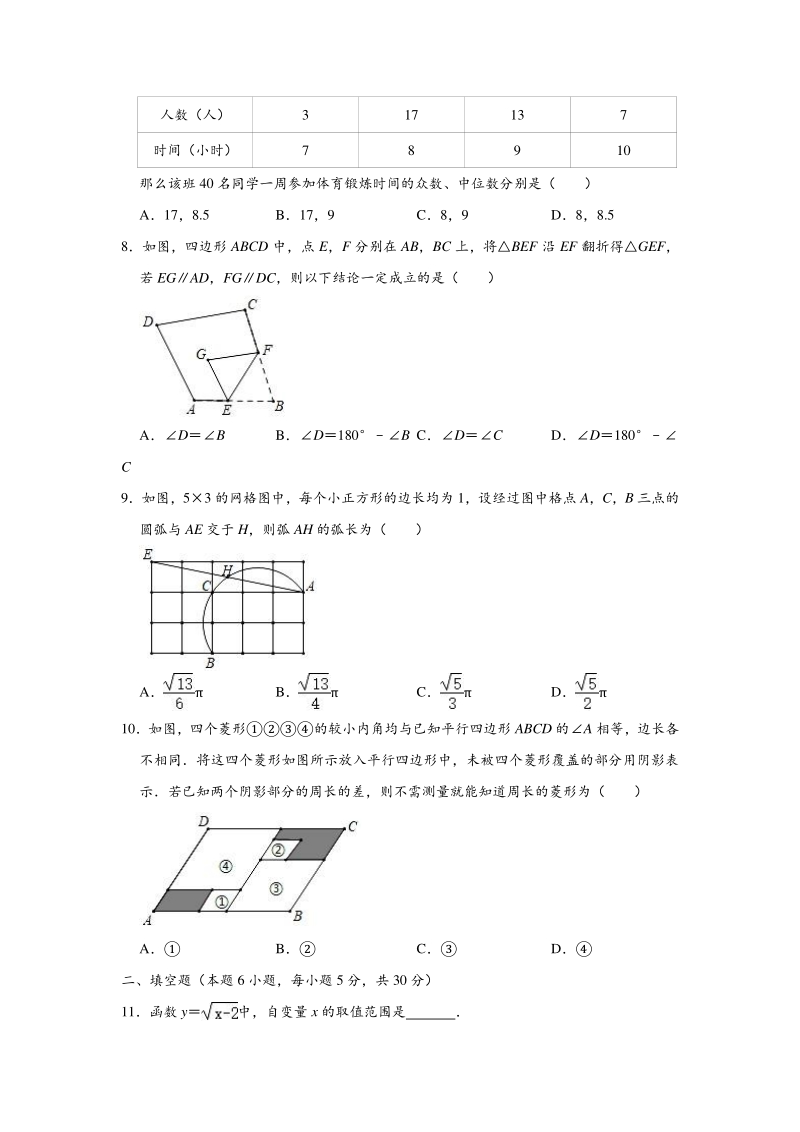
2、） A B C D 6在一个不透明的口袋中，装有若干个红球和 6 个黄球，它们只有颜色不同，摇匀后从中 随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的 频率稳定在 0.6，则估计口袋中大约有红球（ ） A24 个 B10 个 C9 个 D4 个 7某班 40 名同学一周参加体育锻炼时间统计如表所示： 人数（人） 3 17 13 7 时间（小时） 7 8 9 10 那么该班 40 名同学一周参加体育锻炼时间的众数、中位数分别是（ ） A17，8.5 B17，9 C8，9 D8，8.5 8如图，四边形 ABCD 中，点 E，F 分别在 AB，BC 上，将BEF 沿 E
3、F 翻折得GEF， 若 EGAD，FGDC，则以下结论一定成立的是（ ） ADB BD180B CDC DD180 C 9如图，53 的网格图中，每个小正方形的边长均为 1，设经过图中格点 A，C，B 三点的 圆弧与 AE 交于 H，则弧 AH 的弧长为（ ） A B C D 10如图，四个菱形的较小内角均与已知平行四边形 ABCD 的A 相等，边长各 不相同将这四个菱形如图所示放入平行四边形中，未被四个菱形覆盖的部分用阴影表 示若已知两个阴影部分的周长的差，则不需测量就能知道周长的菱形为（ ） A B C D 二、填空题（本题 6 小题，每小题 5 分，共 30 分） 11函数 y中，自变量
4、 x 的取值范围是 12分式方程的解是 13已知圆锥的底面半径为 4cm，高为 3cm，则这个圆锥的侧面积为 cm2（结果保 留 ） 14如图，平行四边形 ABCD 中，M，N 分别为边 BC，CD 的中点，且MANABC，则 的值是 15如图，已知平面直角坐标系中 A 点坐标为（0，4），以 OA 为一边在第一象限作平行四 边形 OABC，对角线 AC、OB 相交于点 E，AB2OA若反比例函数 y的图象恰好经 过点 C 和点 E，则 k 的值为 16如图，半径为 2 的O 分别与 x 轴，y 轴交于 A，D 两点，O 上两个动点 B，C，使 BAC60恒成立，设ABC 的重心为 G，则 D
5、G 的最小值是 三、解答题（本题 8 小题，共 80 分.） 17（1）计算：21+2cos30+（3.14）0 （2）先化简，再求值：，其中 x2 18延迟开学期间，学校为了全面分析学生的网课学习情况，进行了一次抽样调查（把学习 情况分为三个层次，A：能主动完成老师布置的作业并合理安排课外时间自主学习；B： 只完成老师布置的作业；C：不完成老师的作业），并将调查结果绘制成图 1 和图 2 的统 计图（不完整）请根据图中提供的信息，解答下列问题： （1）此次抽样调查中，共调查了 名学生； （2）将条形图补充完整； （3）求出图 2 中 C 所占的圆心角的度数； （4）如果学校开学后对 A 层次
6、的学生奖励一次看电影，根据抽样调查结果，请你估计该 校 1500 名学生中大约有多少名学生能获得奖励？ 19如图，直线 yx+m 与二次函数 yax2+2x+c 的图象交于点 A（0，3），已知该二次函 数图象的对称轴为直线 x1 （1）求 m 的值及二次函数解析式； （2）若直线 yx+m 与二次函数 yax2+2x+c 的图象的另一个交点为 B，求OAB 的面 积； （3）根据函数图象回答：x 为何值时该一次函数值大于二次函数值 20如图，BC 是坡角为 30，长为 10 米的一道斜坡，在坡顶灯杆 CD 的顶端 D 处有一探 射灯， 射出的边缘光线 DA和 DB 与水平路面 AB 所成的夹
7、角DAN 和DBN 分别是 45 和 60 （1）求灯杆 CD 的高度； （2）求 AB 的长度（结果保留根号） 21如图，已知O 的直径 AB10，弦 AC6，BAC 的平分线交O 于点 D，过点 D 作 DEAC 交 AC 的延长线于点 E （1）求证：DE 是O 的切线； （2）求 DE 的长 22在“前线医护人员”和全国人民的共同努力下，疫情得到了有效控制，宁波各大企业复 工复产有序进行为了实现员工“一站式”返岗，宁波某企业打算租赁 5 辆客车前往宁 波东站接员工返岗已知现有 A、B 两种客车，A 型客车的载客量为 45 人/辆，每辆租金 为 400 元；B 型客车的载客量为 30 人
8、/辆，每辆租金为 280 元设租用 A 型客车为 x 辆， 所需费用为 y 元 （1）求 y 关于 x 的函数解析式； （2） 若该企业需要接的员工有 205 人， 请求出租车费用最小值， 并写出对应的租车方案 23如图 1，RtABC 中，ABC90，P 是斜边 AC 上一个动点，以 BP 为直径作O 交 BC 于点 D，与 AC 的另一个交点为 E（点 E 在点 P 右侧），连结 DE、BE，已知 AB 3，BC6 （1）求线段 BE 的长； （2）如图 2，若 BP 平分ABC，求BDE 的正切值； （3） 是否存在点 P， 使得BDE 是等腰三角形， 若存在， 求出所有符合条件的 CP
9、 的长； 若不存在，请说明理由 24定义：按螺旋式分别延长 n 边形的 n 条边至一点，若顺次连接这些点所得的图形与原多 边形相似，则称它为原图形的螺旋相似图形例如：如图 1，分别延长多边形 A1A2An 的边得 A1，A2，An，若多边形 A1A2An与多边形 A1A2An 相似，则多 边形 A1A2An就是 A1A2An的螺旋相似图形 （1）如图 2，已知ABC 是等边三角形，作出ABC 的一个螺旋相似图形，简述作法， 并给以证明 （2）如图 3，已知矩形 ABCD，请探索矩形 ABCD 是否存在螺旋相似图形，若存在，求 出此时 AB 与 BC 的比值；若不存在，说明理由 （3）如图 4，
10、ABC 是等腰直角三角形，ACBC2，分别延长 CA，AB，BC 至 A， B，C，使ABC是ABC 的螺旋相似三角形若 AAkAC，请直接写出 BB，CC的长（用含 k 的代数式表示） 参考答案 一.选择题（本大题共 10 小题，每小题 4 分，共 40 分） 15 的相反数是（ ） A B5 C5 D 【分析】根据只有符号不同而绝对值相等两个数互为相反数，可得5 的相反数 解：5 的相反数是 5， 故选：B 2下列运算中正确的是（ ） A2a2 a3a3 B（ab2）2ab4 C2ab2b22a D（a+b）2a2+b2 【分析】根据整式的运算法则即可求出答案 解：（A）原式2a3，故 A
11、 错误 （B）原式a2b4，故 B 错误 （D）原式a2+2ab+b2，故 D 错误 故选：C 3 新冠病毒平均直径为 0.0001 毫米， 但它以飞沫传播为主， 而飞沫的直径是大于 5 微米的， 所以 N95 或医用口罩能起到防护作用，用科学记数法表示 0.0001 毫米是（ ） A0.1105毫米 B104毫米 C103毫米 D0.1103毫米 【分析】绝对值小于 1 的正数也可以利用科学记数法表示，一般形式为 a10n，与较大 数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数 字前面的 0 的个数所决定 解：0.0001 毫米104毫米； 故选：B 4一个不等
12、式的解集为1x2，那么在数轴上表示正确的是（ ） A B C D 【分析】根据数轴上的点表示的数，右边的总是大于左边的数这个解集就是不等式 x 1 和 x2 的解集的公共部分 解：数轴上1x2 表示1 与 2 之间的部分，并且包含 2，不包含1，在数轴上可表 示为： 故选：A 5某露天舞台如图所示，它的俯视图是（ ） A B C D 【分析】找到从上面看，所得到的图形即可 解：该几何体的俯视图为 故选：D 6在一个不透明的口袋中，装有若干个红球和 6 个黄球，它们只有颜色不同，摇匀后从中 随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的 频率稳定在 0.6，则估计口
13、袋中大约有红球（ ） A24 个 B10 个 C9 个 D4 个 【分析】设口袋中红球有 x 个，用黄球的个数除以球的总个数等于摸到黄球的频率，据 此列出关于 x 的方程，解之可得答案 解：设口袋中红球有 x 个， 根据题意，得：0.6， 解得 x4， 经检验：x4 是分式方程的解， 所以估计口袋中大约有红球 4 个， 故选：D 7某班 40 名同学一周参加体育锻炼时间统计如表所示： 人数（人） 3 17 13 7 时间（小时） 7 8 9 10 那么该班 40 名同学一周参加体育锻炼时间的众数、中位数分别是（ ） A17，8.5 B17，9 C8，9 D8，8.5 【分析】根据中位数、众数的
14、概念分别求得这组数据的中位数、众数 解：众数是一组数据中出现次数最多的数，即 8； 由统计表可知，处于 20，21 两个数的平均数就是中位数， 这组数据的中位数为8.5； 故选：D 8如图，四边形 ABCD 中，点 E，F 分别在 AB，BC 上，将BEF 沿 EF 翻折得GEF， 若 EGAD，FGDC，则以下结论一定成立的是（ ） ADB BD180B CDC DD180 C 【分析】依据平行线的性质，即可得到BEGA，BFGC，再根据四边形内角 和为 360，即可得到D 的度数 解：GFCD，GEAD， BEGA，BFGC， 由折叠可得：BG， 四边形 BEGF 中，B+G2B360BE
15、GBFG， 四边形 ABCD 中，B+D360AC， 2BB+D， BD， 故选：A 9如图，53 的网格图中，每个小正方形的边长均为 1，设经过图中格点 A，C，B 三点的 圆弧与 AE 交于 H，则弧 AH 的弧长为（ ） A B C D 【分析】 连接 EB， BH， AB， 根据勾股定理得到 BEAB， AE ，根据勾股定理的逆定理得到ABE 是等腰直角三角形，根据弧长公式即可得到 结论 解：连接 EB，BH，AB， BEAB，AE， BE2+AB2AE2， ABE90， ABE 是等腰直角三角形， ACB90， AB 是圆的直径， AHB90， BHAH， ABHBAH45， 弧 A
16、H 所对的圆心角为 90， 的长 故选：B 10如图，四个菱形的较小内角均与已知平行四边形 ABCD 的A 相等，边长各 不相同将这四个菱形如图所示放入平行四边形中，未被四个菱形覆盖的部分用阴影表 示若已知两个阴影部分的周长的差，则不需测量就能知道周长的菱形为（ ） A B C D 【分析】设四个菱形的边长分别为 a、b、c、d，设已知两个阴影部分的周长 的差为 l，分别用 a，b，c，d 表示出右上角和左下角阴影部分的周长，合并同类项，即 可得出答案 解：设四个菱形的边长分别为 a、b、c、d，设已知两个阴影部分的周长的差 为 l，由题意得： （a+dbc）+b+b+（a+dc）+c+（cb
17、）（da）+（da）+a+al， 整理得：2al 若已知两个阴影部分的周长的差，则不需测量就能知道周长的菱形为， 故选：A 二、填空题（本题 6 小题，每小题 5 分，共 30 分） 11函数 y中，自变量 x 的取值范围是 x2 【分析】根据二次根式的性质，被开方数大于等于 0，就可以求解 解：依题意，得 x20， 解得：x2， 故答案为：x2 12分式方程的解是 x6 【分析】分式方程去分母转化为整式方程，求出整式方程的解得到 x 的值，经检验即可 得到分式方程的解 解：去分母得：3x2x6， 解得：x6， 经检验 x6 是分式方程的解， 故答案为：x6 13已知圆锥的底面半径为 4cm，
18、高为 3cm，则这个圆锥的侧面积为 20 cm2（结果保 留 ） 【分析】 利用勾股定理易求得圆锥的母线长， 那么圆锥的侧面积底面周长母线长2， 把相应数值代入即可求解 解：圆锥的底面半径为 4cm，高为 3cm， 母线长为 5cm， 圆锥的侧面积为 245220cm2 14如图，平行四边形 ABCD 中，M，N 分别为边 BC，CD 的中点，且MANABC，则 的值是 【分析】延长 AM 与 DC 的延长线交于点 E，先证明ABMECM，得 AM 与 AE 的关 系，AB 与 EN 和 ED 的关系，再证明 EANEDA，由相似三角形比例线段便可得结论 解：延长 AM 与 DC 的延长线交于
19、点 E， 四边形 ABCD 为平行四边形， ABCD，ABCD，BD， BMAN， ECMBMAND， M 是 BC 的中点，N 是 CD 的中点， BMCM，CNDN， 在ABM 和ECM 中， ， ABMECM（ASA）， ABCE，AMEM， AE2AM，ENAB，ED2AB， EAND，EE， EANEDA， ，即 EA2ED EN， ， ， 故答案为： 15如图，已知平面直角坐标系中 A 点坐标为（0，4），以 OA 为一边在第一象限作平行四 边形 OABC，对角线 AC、OB 相交于点 E，AB2OA若反比例函数 y的图象恰好经 过点 C 和点 E，则 k 的值为 【分析】 过点
20、C 作 CDx 轴于点 D， 由已知条件及平行四边形的性质可得 BCOA4， OCAB8，设 C（x，），则点 E（，），点 B（x，+4），分别按照点 E 在 反比例函数图象上和作为线段 BD 的中点，用两种方式表示出点 E 的纵坐标，从而得到 关于 x 和 k 的等式， 解得 x 和 k 的关系， 再在 RtCOD 中， 由勾股定理得关于 k 的方程， 解得 k 的值，舍去负值，即可得出答案 解：如图，过点 C 作 CDx 轴于点 D， A 点坐标为（0，4），AB2OA OA4，AB8， 四边形 OABC 为平行四边形， BCOA4，OCAB8，点 B、C、D 共线， 反比例函数 y的图
21、象恰好经过点 C 和点 E， 设 C（x，），则点 E（，），点 B（x，+4）， E 为平行四边形对角线的交点， E 为 OB 中点， 点 E 的坐标又可以表示为：（，+2）， +2， 解得：， x， 在 RtCOD 中，由勾股定理得： +64， 解得 k（负值舍去，因为反比例函数图象位于第一象限） 故答案为： 16如图，半径为 2 的O 分别与 x 轴，y 轴交于 A，D 两点，O 上两个动点 B，C，使 BAC60恒成立，设ABC 的重心为 G，则 DG 的最小值是 【分析】连接 AG 并延长，交 BC 于点 F，由ABC 的重心为 G，可知 F 为 BC 的中点， 再由垂径定理可知 O
22、FBC，从而可求得 OF 的长；在 AO 上取点 E，使 AEAO，连 接 GE，可判定AGEAFO，由相似三角形的性质列出比例式，求得 GE 的长，进而 可得点 E 的坐标，利用勾股定理求出 DE 的长，根据 G 在以 E 为圆心，为半径的圆上 运动，可知 DG 的最小值为 DE 的长减去，计算即可 解：连接 AG 并延长，交 BC 于点 F， ABC 的重心为 G， F 为 BC 的中点， OFBC， BAC60， BOF60， OBF30， OFOB1， ABC 的重心为 G， AGAF， 在 AO 上取点 E，使 AEAO，连接 GE， ，FAOGAE， AGEAFO， ， GE G
23、在以 E 为圆心，为半径的圆上运动， E（，0）， DE， DG 的最小值是， 故答案为： 三、解答题（本题 8 小题，共 80 分.） 17（1）计算：21+2cos30+（3.14）0 （2）先化简，再求值：，其中 x2 【分析】（1）根据负整数指数幂的运算法则、特殊角的三角函数值、零指数幂的运算法 则、二次根式的性质计算； （2）根据分式的加减混合运算法则把原式化简，代入计算得到答案 解：（1）21+2cos30+（3.14）0 +2+12 +12 ； （2） x ， 当 x2 时，原式4 18延迟开学期间，学校为了全面分析学生的网课学习情况，进行了一次抽样调查（把学习 情况分为三个层次
24、，A：能主动完成老师布置的作业并合理安排课外时间自主学习；B： 只完成老师布置的作业；C：不完成老师的作业），并将调查结果绘制成图 1 和图 2 的统 计图（不完整）请根据图中提供的信息，解答下列问题： （1）此次抽样调查中，共调查了 200 名学生； （2）将条形图补充完整； （3）求出图 2 中 C 所占的圆心角的度数； （4）如果学校开学后对 A 层次的学生奖励一次看电影，根据抽样调查结果，请你估计该 校 1500 名学生中大约有多少名学生能获得奖励？ 【分析】（1）通过对比条形统计图和扇形统计图可知：学习态度层级为 A 的有 50 人， 占调查学生的 25%，即可求得总人数； （2）由
25、（1）可知：C 人数为：2001205030 人，将图补充完整即可； （3）各个扇形的圆心角的度数360该部分占总体的百分比，所以可以求出：360 （125%60%）54； （4）从扇形统计图可知，A 层次的学生数占得百分比为 25%，再估计该市近 1500 名初 中生中能获得奖励学生数就很容易了 解：（1）5025%200（人） 答：共调查了 200 名学生， 故答案为：200； （2）C 人数：2001205030（人） 条形统计图如图所示： （3）C 所占圆心角度数360（125%60%）54 （4）150025%375（人） 答：该校学生中大约有 375 名学生能获得奖励 19如图，直
26、线 yx+m 与二次函数 yax2+2x+c 的图象交于点 A（0，3），已知该二次函 数图象的对称轴为直线 x1 （1）求 m 的值及二次函数解析式； （2）若直线 yx+m 与二次函数 yax2+2x+c 的图象的另一个交点为 B，求OAB 的面 积； （3）根据函数图象回答：x 为何值时该一次函数值大于二次函数值 【分析】（1）根据待定系数法即可求得 m 的值及二次函数解析式； （2）解析式联立组成方程组，解方程组求得 B 的坐标，然后根据三角形面积公式求得即 可； （3）根据图象即可求得 解：（1）直线 yx+m 经过点 A（0，3）， m3， 直线为 yx+3， 二次函数 yax2+
27、2x+c 的图象经过点 A（0，3），且对称轴为直线 x1 ，解得， 二次函数解析式为 yx2+2x+3； （2）解得或， B（1，4）， OAB 的面积； （3）由图象可知：当 x0 或 x1 时，该一次函数值大于二次函数值 20如图，BC 是坡角为 30，长为 10 米的一道斜坡，在坡顶灯杆 CD 的顶端 D 处有一探 射灯， 射出的边缘光线 DA和 DB 与水平路面 AB 所成的夹角DAN 和DBN 分别是 45 和 60 （1）求灯杆 CD 的高度； （2）求 AB 的长度（结果保留根号） 【分析】（1）延长 DC 交 AN 于 H只要证明 BCCD 即可； （2）在 RtBCH 中，
28、求出 BH、CH，在 RtADH 中求出 AH 即可解决问题 解：（1）延长 DC 交 AN 于 H DBH60，DHB90， BDH30， CBH30， CBDBDC30， BCCD10（米） （2）在 RtBCH 中，CHBC5，BH5， DH15， 在 RtADH 中，AH15， ABAHBH15105（米） 答：AB 的长度约为 5 米 21如图，已知O 的直径 AB10，弦 AC6，BAC 的平分线交O 于点 D，过点 D 作 DEAC 交 AC 的延长线于点 E （1）求证：DE 是O 的切线； （2）求 DE 的长 【分析】（1）连接 OD，欲证明 DE 是O 的切线，只要证明
29、ODDE 即可 （2）过点 O 作 OFAC 于点 F，只要证明四边形 OFED 是矩形即可得到 DEOF，在 RTAOF 中利用勾股定理求出 OF 即可 【解答】证明：（1）连接 OD， AD 平分BAC， DAEDAB， OAOD，ODADAO， ODADAE， ODAE， DEAC， ODDE， DE 是O 切线 （2）过点 O 作 OFAC 于点 F， AFCF3， OF4 OFEDEFODE90， 四边形 OFED 是矩形， DEOF4 22在“前线医护人员”和全国人民的共同努力下，疫情得到了有效控制，宁波各大企业复 工复产有序进行为了实现员工“一站式”返岗，宁波某企业打算租赁 5
30、辆客车前往宁 波东站接员工返岗已知现有 A、B 两种客车，A 型客车的载客量为 45 人/辆，每辆租金 为 400 元；B 型客车的载客量为 30 人/辆，每辆租金为 280 元设租用 A 型客车为 x 辆， 所需费用为 y 元 （1）求 y 关于 x 的函数解析式； （2） 若该企业需要接的员工有 205 人， 请求出租车费用最小值， 并写出对应的租车方案 【分析】（1）根据总费用A 型看成的费用+B 型客车的费用，即可解决问题 （2）列出不等式求出 x 的范围，再根据 x 是整数，求出 x 的值，根据一次函数的性质即 可解决问题 解：（1）设租用 A 型客车为 x 辆，则租用 B 型客车为
31、（5x）辆， 由题意得：y400x+280（5x）120x+1400 （2）由题意：45x+30（5x）205，解得 x， 而费用 y120x+1400， x 为整数，x 取最小，费用 y 最低， x4， 方案为租用 A 型客车 4 辆，租用 B 型客车 1 辆 23如图 1，RtABC 中，ABC90，P 是斜边 AC 上一个动点，以 BP 为直径作O 交 BC 于点 D，与 AC 的另一个交点为 E（点 E 在点 P 右侧），连结 DE、BE，已知 AB 3，BC6 （1）求线段 BE 的长； （2）如图 2，若 BP 平分ABC，求BDE 的正切值； （3） 是否存在点 P， 使得BDE
32、 是等腰三角形， 若存在， 求出所有符合条件的 CP 的长； 若不存在，请说明理由 【分析】（1）求出 AC3，由三角形 ABC 的面积可求出 BE 的长； （2）连接 DP，证明CPDCAB，得出2，设 DPBDx，则 CD2x， 由 CB3x6，得出 x2，根据 tanBDEtanBPE 可得出答案； （3）分三种情况，求出 CPCD，求出 CD，可得出答案 解：（1）ABC90，AB3，BC6， AC3， BP 为O 的直径， BEP90， BEAC， SABC ABAC， BE； （2）BP 平分ABC， DBPABC45， 连接 DP，如图 1， BP 为O 的直径， DBPDPB4
33、5， 可设 DPBDx， CDPABC90 PDAB， CPDCAB， 2， CD2x， CB3x6， x2， DPBD2，CD4， CP2， CE， tanBDEtanBPE3 （3）解：存在这样的点 P 由DCPBCA，得， CPCD， 若BDE 是等腰三角形，可分三种情况： 当 BDBE 时，BDBE， CDBCBD6， CP33 当 BDDE 时，此时点 D 是 RtCBE 斜边的中点， CDBC3， CP； 当 DEBE 时，作 EHBC 于点 H，则 H 是 BD 的中点， ABCEHC90， EHAB， ， 又AEACCE3， BHDH， CD6， CP 综上所述，BDE 是等腰
34、三角形，符合条件的 CP 的长为 33 或或 24定义：按螺旋式分别延长 n 边形的 n 条边至一点，若顺次连接这些点所得的图形与原多 边形相似，则称它为原图形的螺旋相似图形例如：如图 1，分别延长多边形 A1A2An 的边得 A1，A2，An，若多边形 A1A2An与多边形 A1A2An 相似，则多 边形 A1A2An就是 A1A2An的螺旋相似图形 （1）如图 2，已知ABC 是等边三角形，作出ABC 的一个螺旋相似图形，简述作法， 并给以证明 （2）如图 3，已知矩形 ABCD，请探索矩形 ABCD 是否存在螺旋相似图形，若存在，求 出此时 AB 与 BC 的比值；若不存在，说明理由 （
35、3）如图 4，ABC 是等腰直角三角形，ACBC2，分别延长 CA，AB，BC 至 A， B，C，使ABC是ABC 的螺旋相似三角形若 AAkAC，请直接写出 BB，CC的长（用含 k 的代数式表示） 【分析】（1）如图 2 中，延长 AB 到 E，延长 BC 到 F，延长 CA 到 D，使得 BECF AD，连接 EF，DF，DE则DEF 是ABC 的一个螺旋相似图形，证明DEF 是等边 三角形即可解决问题 （2）如图 3 中，假设存在四边形 EFGH 是矩形 ABCD 的螺旋相似图形，设 ABCD a，BCADb，BEDGx，CFAHy分两种情形，利用相似三角形的性质以 及相似矩形的性质，
36、构建关系式证明 ab 即可解决问题 （3）如图 4 中，作 BTCB 交 CB 的延长线于 T设 TBTBm，证明ACC ATB（ASA），推出 ACTC，CCTBBT，构建关系式推出 mk 即 可解决问题 解：（1）如图 2 中，延长 AB 到 E，延长 BC 到 F，延长 CA 到 D，使得 BECFAD， 连接 EF，DF，DE则DEF 是ABC 的一个螺旋相似图形 理由：ABC 是等边三角形， ABBCAC，CABABCACB， DAEFCDEBF120， BECFAD， CDAEBF， FCDDAEEBF（SAS）， DFDEEF， DEF 是等边三角形， DEFABC， DEF 是
37、ABC 的一个螺旋相似图形 （2）如图 3 中，假设存在四边形 EFGH 是矩形 ABCD 的螺旋相似图形，设 ABCD a，BCADb，BEDGx，CFAHy 由题意：BEFAHE， ， ， 当时， x y，ax+x2by+y2， by+ y2by+y2， a2b2， ab，即 AB：BC1 当时， x y，ax+x2by+y2， y+ y2by+y2， y（1+）0， y0，1+0， a2b2， ab，即 AB：BC1， 综上所述，AB：BC1 （3）如图 4 中，作 BTCB 交 CB 的延长线于 T ACBC2，ACB90， ABCCAB45， TBBABC45， TBBTBB45， TBTB，设 TBTBm， ABC是ABC 的螺旋相似三角形， ACBC，ACB90， ACC+BC90，ACC+CAC90， CACBCT， ACCT90， ACCATB（ASA）， ACTC，CCTBBT， 2+2k2+2m， mk， BBk，CCk
