1、2020 年山东省东营市中考数学模拟试卷年山东省东营市中考数学模拟试卷 一选择题（共一选择题（共 10 小题）小题） 1的倒数是（ ） A B C D 2国家发改委 2 月 7 日紧急下达第二批中央预算内投资 200000000 元人民币，专项补助承 担重症感染患者救治任务的湖北多家医院重症治疗病区建设，其中数据 200000000 用科 学记数法表示为（ ） A2107 B2108 C20107 D0.2108 3为全力抗战疫情，响应政府“停课不停学”号召，东营市教育局发布关于疫情防控期间 开展在线课程教学的通知：从 2 月 10 日开始，全市中小学按照教学计划，开展在线课程 教学和答疑据互
2、联网后台数据显示，某中学九年级七科老师 2 月 10 日在线答疑问题总 个数如下表所示，则 2 月 10 日该中学九年级七科老师在线答疑问题总个数的平均数是 （ ） 学科 语文 数学 英语 物理 化学 道法 历史 数量/个 26 28 28 26 24 21 22 A22 B24 C25 D26 4如图，一个圆形转盘被平均分成 6 个全等的扇形，任意旋转这个转盘 1 次，则当转盘停 止转动时，指针指向阴影部分的概率是（ ） A B C D 5一个物体的三视图如图所示，其中主视图和左视图是全等的等边三角形，俯视图是圆， 根据图中所示数据，可求这个物体的表面积为（ ） A B2 C3 D （+1）
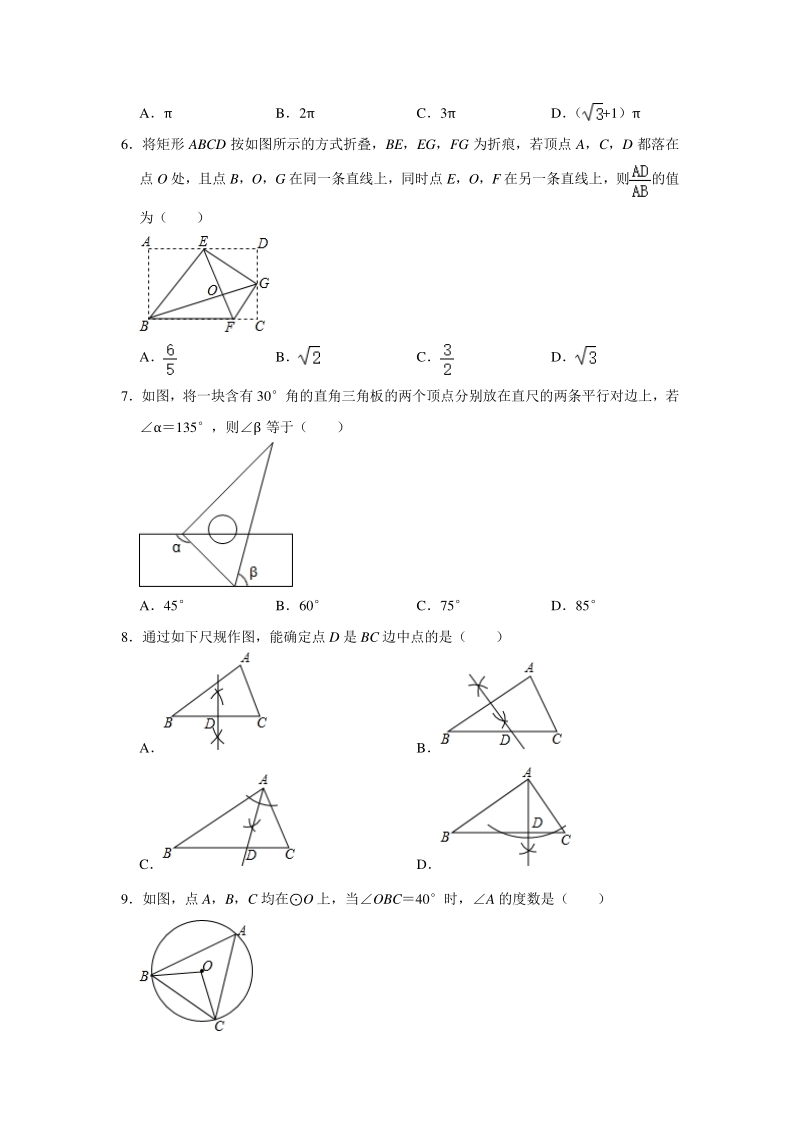
3、 6将矩形 ABCD 按如图所示的方式折叠，BE，EG，FG 为折痕，若顶点 A，C，D 都落在 点 O 处，且点 B，O，G 在同一条直线上，同时点 E，O，F 在另一条直线上，则的值 为（ ） A B C D 7如图，将一块含有 30角的直角三角板的两个顶点分别放在直尺的两条平行对边上，若 135，则 等于（ ） A45 B60 C75 D85 8通过如下尺规作图，能确定点 D 是 BC 边中点的是（ ） A B C D 9如图，点 A，B，C 均在O 上，当OBC40时，A 的度数是（ ） A50 B55 C60 D65 10如图，抛物线 yax2+bx+c（a0）与 x 轴交于点（3，
4、0） ，其对称轴为直线 x， 结合图象分析下列结论： abc0； 3a+c0； 当 x0 时，y 随 x 的增大而增大； 一元二次方程 cx2+bx+a0 的两根分别为 x1，x2； 0； 若 m，n（mn）为方程 a（x+3） （x2）+30 的两个根，则 m3 且 n2， 其中正确的结论有（ ） A3 个 B4 个 C5 个 D6 个 二填空题（共二填空题（共 8 小题）小题） 11某班学生经常采用“小组合作学习”的方式进行学习，王老师每周对各小组合作学习的 情况进行综合评分下表是各小组其中一周的得分情况： 组别 一 二 三 四 五 六 七 八 得分 90 95 90 88 90 92 8
5、5 90 这组数据的众数是 12若 x2+ax+4（x2）2，则 a 13在“践行生态文明，你我一起行动”主题有奖竞赛活动中，东营某实验中学九年级组共 设置“生态知识、生态技能、生态习惯、生态文化”四个类别的竞赛内容，如果参赛同 学抽到每一类别的可能性相同，那么小宇参赛时抽到“生态知识”的概率是 14关于 x 的分式方程3 的解为非负数，则 a 的取值范围为 15 等腰ABC 中， BDAC， 垂足为点 D， 且 BDAC， 则等腰ABC 底角的度数为 16如图，在平面直角坐标系中，反比例 y（k0）的图象和ABC 都在第一象限内， ABAC，BCx 轴，且 BC4，点 A 的坐标为（3，5）
6、 若将ABC 向下平移 m 个 单位长度，A，C 两点同时落在反比例函数图象上，则 m 的值为 17如图，平面直角坐标系中，点 B 在第一象限，点 A 在 x 轴的正半轴上，AOBB 30，OA2，将AOB 绕点 O 逆时针旋转 90，点 B 的对应点 B的坐标是 18如图，直线 l：yx+1 分别交 x 轴、y 轴于点 A 和点 A1，过点 A1作 A1B1l，交 x 轴于点 B1，过点 B1作 B1A2x 轴，交直线 l 于点 A2；过点 A2作 A2B2l，交 x 轴于点 B2，过点 B2作 B2A3x 轴，交直线 l 于点 A3，依此规律，若图中阴影A1OB1的面积 为 S1，阴影A2
7、B1B2的面积为 S2，阴影A3B2B3的面积为 S3，则 Sn 三解答题（共三解答题（共 7 小题）小题） 19 （1）计算： （1）2019+tan60+（3.14）0 （2）解不等式组，并求此不等式组的整数解 20 齐齐哈尔市教育局想知道某校学生对扎龙自然保护区的了解程度， 在该校随机抽取了部 分学生进行问卷， 问卷有以下四个选项： A 十分了解； B 了解较多： C 了解较少： D 不 了解（要求：每名被调查的学生必选且只能选择一项） 现将调查的结果绘制成两幅不完 整的统计图请根据两幅统计图中的信息回答下列问题： （1）本次被抽取的学生共有 名； （2）请补全条形图； （3）扇形图中的
8、选项“C了解较少”部分所占扇形的圆心角的大小为 ； （4） 若该校共有 2000 名学生， 请你根据上述调查结果估计该校对于扎龙自然保护区 “十 分了解”和“了解较多”的学生共有多少名？ 21 某网店专售一款电动牙刷， 其成本为 20 元/支， 销售中发现， 该商品每天的销售量 y （支） 与销售单价 x（元/支）之间存在如图所示的关系 （1）请求出 y 与 x 的函数关系式； （2）该款电动牙刷销售单价定为多少元时，每天销售利润最大？最大利润是多少元？ （3）近期武汉爆发了“新型冠状病毒”疫情，该网店店主决定从每天获得的利润中抽出 200 元捐赠给武汉， 为了保证捐款后每天剩余利润不低于 5
9、50 元， 如何确定该款电动牙刷 的售单价？ 22如图，点 O 是线段 AH 上一点，AH3，以点 O 为圆心，OA 的长为半径作O，过点 H 作 AH 的垂线交O 于 C，N 两点，点 B 在线段 CN 的延长线上，连接 AB 交O 于点 M，以 AB，BC 为边作ABCD （1）求证：AD 是O 的切线； （2）若 OHAH，求四边形 AHCD 与O 重叠部分的面积； （3）若 NHAH，BN，连接 MN，求 OH 和 MN 的长 23某商店购进 A、B 两种商品，购买 1 个 A 商品比购买 1 个 B 商品多花 10 元，并且花费 300 元购买 A 商品和花费 100 元购买 B 商
10、品的数量相等 （1）求购买一个 A 商品和一个 B 商品各需要多少元； （2） 商店准备购买 A、 B 两种商品共 80 个， 若 A 商品的数量不少于 B 商品数量的 4 倍， 并且购买 A、 B 商品的总费用不低于 1000 元且不高于 1050 元， 那么商店有哪几种购买方 案？ 24如图 1，在矩形 ABCD 中，BC3，动点 P 从 B 出发，以每秒 1 个单位的速度，沿射线 BC 方向移动，作PAB 关于直线 PA 的对称PAB，设点 P 的运动时间为 t（s） （1）若 AB2 如图 2，当点 B落在 AC 上时，显然PAB是直角三角形，求此时 t 的值； 是否存在异于图 2 的
11、时刻，使得PCB是直角三角形？若存在，请直接写出所有符 合题意的 t 的值？若不存在，请说明理由 （2）当 P 点不与 C 点重合时，若直线 PB与直线 CD 相交于点 M，且当 t3 时存在某 一时刻有结论PAM45成立， 试探究： 对于 t3 的任意时刻， 结论 “PAM45” 是否总是成立？请说明理由 25如图，抛物线 yx2+bx+c 与直线 yx+3 分别相交于 A，B 两点，且此抛物线与 x 轴的一个交点为 C，连接 AC，BC已知 A（0，3） ，C（3，0） （1）求抛物线的解析式； （2）在抛物线对称轴 l 上找一点 M，使|MBMC|的值最大，并求出这个最大值； （3）点
12、P 为 y 轴右侧抛物线上一动点，连接 PA，过点 P 作 PQPA 交 y 轴于点 Q，问： 是否存在点 P 使得以 A，P，Q 为顶点的三角形与ABC 相似？若存在，请求出所有符合 条件的点 P 的坐标；若不存在，请说明理由 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 10 小题）小题） 1的倒数是（ ） A B C D 【分析】根据倒数定义可知，的倒数是 【解答】解：的倒数是 故选：A 2国家发改委 2 月 7 日紧急下达第二批中央预算内投资 200000000 元人民币，专项补助承 担重症感染患者救治任务的湖北多家医院重症治疗病区建设，其中数据 200000000
13、用科 学记数法表示为（ ） A2107 B2108 C20107 D0.2108 【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相 同当原数绝对值1 时，n 是正数；当原数的绝对值1 时，n 是负数 【解答】解：将 200000000 用科学记数法表示为：2108 故选：B 3为全力抗战疫情，响应政府“停课不停学”号召，东营市教育局发布关于疫情防控期间 开展在线课程教学的通知：从 2 月 10 日开始，全市中小学按照教学计划，开展在线课程 教学和答疑据互联网后台数据显示，
14、某中学九年级七科老师 2 月 10 日在线答疑问题总 个数如下表所示，则 2 月 10 日该中学九年级七科老师在线答疑问题总个数的平均数是 （ ） 学科 语文 数学 英语 物理 化学 道法 历史 数量/个 26 28 28 26 24 21 22 A22 B24 C25 D26 【分析】要求平均数只要求出数据之和再除以总个数即可 【解答】解： （26+28+28+26+24+21+22）7 1757 25 故选：C 4如图，一个圆形转盘被平均分成 6 个全等的扇形，任意旋转这个转盘 1 次，则当转盘停 止转动时，指针指向阴影部分的概率是（ ） A B C D 【分析】用阴影部分扇形个数除以扇形
15、的总个数即可得 【解答】解：当转盘停止转动时，指针指向阴影部分的概率是， 故选：D 5一个物体的三视图如图所示，其中主视图和左视图是全等的等边三角形，俯视图是圆， 根据图中所示数据，可求这个物体的表面积为（ ） A B2 C3 D （+1） 【分析】由三视图可知：该几何体是一个圆锥，其轴截面是一个高为的正三角形可 计算边长为 2，据此即可得出表面积 【解答】 解： 由三视图可知： 该几何体是一个圆锥， 其轴截面是一个高为的正三角形 正三角形的边长2 圆锥的底面圆半径是 1，母线长是 2， 底面周长为 2 侧面积为222，底面积为 r2， 全面积是 3 故选：C 6将矩形 ABCD 按如图所示的
16、方式折叠，BE，EG，FG 为折痕，若顶点 A，C，D 都落在 点 O 处，且点 B，O，G 在同一条直线上，同时点 E，O，F 在另一条直线上，则的值 为（ ） A B C D 【分析】由折叠可得，E，G 分别为 AD，CD 的中点，设 CD2a，AD2b，根据 Rt BCG 中，CG2+BC2BG2，可得即 a2+（2b）2（3a）2，进而得出的值 【解答】解：由折叠可得，AEOEDE，CGOGDG， E，G 分别为 AD，CD 的中点， 设 CD2a，AD2b，则 AB2aOB，DGOGCGa，BG3a，BCAD2b， C90， RtBCG 中，CG2+BC2BG2， 即 a2+（2b）
17、2（3a）2， b22a2， 即 ba， ， 的值为， 故选：B 7如图，将一块含有 30角的直角三角板的两个顶点分别放在直尺的两条平行对边上，若 135，则 等于（ ） A45 B60 C75 D85 【分析】直接利用平行线的性质以及三角形的性质进而得出答案 【解答】解：由题意可得：135， 145， 180456075 故选：C 8通过如下尺规作图，能确定点 D 是 BC 边中点的是（ ） A B C D 【分析】作线段 BC 的垂直平分线可得线段 BC 的中点 【解答】解：作线段 BC 的垂直平分线可得线段 BC 的中点 由此可知：选项 A 符合条件， 故选：A 9如图，点 A，B，C
18、均在O 上，当OBC40时，A 的度数是（ ） A50 B55 C60 D65 【分析】先利用等腰三角形的性质和三角形内角和计算出BOC 的度数，然后根据圆周 角定理可得到A 的度数 【解答】解：OBOC， OCBOBC40， BOC1804040100， ABOC50 故选：A 10如图，抛物线 yax2+bx+c（a0）与 x 轴交于点（3，0） ，其对称轴为直线 x， 结合图象分析下列结论： abc0； 3a+c0； 当 x0 时，y 随 x 的增大而增大； 一元二次方程 cx2+bx+a0 的两根分别为 x1，x2； 0； 若 m，n（mn）为方程 a（x+3） （x2）+30 的两个
19、根，则 m3 且 n2， 其中正确的结论有（ ） A3 个 B4 个 C5 个 D6 个 【分析】利用二次函数图象与系数的关系，结合图象依次对各结论进行判断 【解答】解：抛物线 yax2+bx+c（a0）与 x 轴交于点（3，0） ，其对称轴为直线 x 抛物线 yax2+bx+c（a0）与 x 轴交于点（3，0）和（2，0） ，且 ab 由图象知：a0，c0，b0 abc0 故结论正确； 抛物线 yax2+bx+c（a0）与 x 轴交于点（3，0） 9a3b+c0 ab c6a 3a+c3a0 故结论正确； 当 x时，y 随 x 的增大而增大；当x0 时，y 随 x 的增大而减小 结论错误；
20、cx2+bx+a0，c0 x2+x+10 抛物线 yax2+bx+c（a0）与 x 轴交于点（3，0）和（2，0） ax2+bx+c0 的两根是3 和 2 1，6 x2+x+10 即为：6x2+x+10，解得 x1，x2； 故结论正确； 当 x时，y0 0 故结论正确； 抛物线 yax2+bx+c（a0）与 x 轴交于点（3，0）和（2，0） ， yax2+bx+ca（x+3） （x2） m，n（mn）为方程 a（x+3） （x2）+30 的两个根 m，n（mn）为方程 a（x+3） （x2）3 的两个根 m，n（mn）为函数 ya（x+3） （x2）与直线 y3 的两个交点的横坐标 结合图象
21、得：m3 且 n2 故结论成立； 故选：C 二填空题（共二填空题（共 8 小题）小题） 11某班学生经常采用“小组合作学习”的方式进行学习，王老师每周对各小组合作学习的 情况进行综合评分下表是各小组其中一周的得分情况： 组别 一 二 三 四 五 六 七 八 得分 90 95 90 88 90 92 85 90 这组数据的众数是 90 【分析】众数是一组数据中出现次数最多的数 【解答】解：90 出现了 4 次，出现的次数最多，则众数是 90； 故答案为：90 12若 x2+ax+4（x2）2，则 a 4 【分析】直接利用完全平方公式得出 a 的值 【解答】解：x2+ax+4（x2）2， a4 故
22、答案为：4 13在“践行生态文明，你我一起行动”主题有奖竞赛活动中，东营某实验中学九年级组共 设置“生态知识、生态技能、生态习惯、生态文化”四个类别的竞赛内容，如果参赛同 学抽到每一类别的可能性相同，那么小宇参赛时抽到“生态知识”的概率是 【分析】直接利用概率公式计算得出答案 【解答】解：共设置“生态知识、生态技能、生态习惯、生态文化”四个类别的竞赛 内容，参赛同学抽到每一类别的可能性相同， 小宇参赛时抽到“生态知识”的概率是： 故答案为： 14 关于x的分式方程3的解为非负数， 则a的取值范围为 a4且a3 【分析】根据解分式方程的方法和方程3 的解为非负数，可以求得 a 的取 值范围 【解
23、答】解：3， 方程两边同乘以 x1，得 2xa+13（x1） ， 去括号，得 2xa+13x3， 移项及合并同类项，得 x4a， 关于 x 的分式方程3 的解为非负数，x10， ， 解得，a4 且 a3， 故答案为：a4 且 a3 15 等腰ABC 中， BDAC， 垂足为点 D， 且 BDAC， 则等腰ABC 底角的度数为 15 或 45或 75 【分析】分点 B 是顶角顶点、点 B 是底角顶点、BD 在ABC 外部和 BD 在ABC 内部 三种情况，根据等腰三角形的性质、直角三角形的性质计算 【解答】解：如图 1，当点 B 是顶角顶点时， ABBC，BDAC， ADCD， BDAC， BD
24、ADCD， 在 RtABD 中，AABD（18090）45； 如图 2，当点 B 是底角顶点，且 BD 在ABC 外部时， BDAC，ACBC， BDBC， BCD30， ABCBAC3015； 如图 3，当点 B 是底角顶点，且 BD 在ABC 内部时， BDAC，ACBC， BDBC， C30， ABCBAC（18030）75； 故答案为：15或 45或 75 16如图，在平面直角坐标系中，反比例 y（k0）的图象和ABC 都在第一象限内， ABAC，BCx 轴，且 BC4，点 A 的坐标为（3，5） 若将ABC 向下平移 m 个 单位长度，A，C 两点同时落在反比例函数图象上，则 m 的
25、值为 【分析】根据已知求出 B 与 C 点坐标，再表示出相应的平移后 A 与 C 坐标，将之代入反 比例函数表达式即可求解； 【解答】解：ABAC，BC4，点 A（3，5） B（1，） ，C（5，） ， 将ABC 向下平移 m 个单位长度， A（3，5m） ，C（5，m） ， A，C 两点同时落在反比例函数图象上， 3（5m）5（m） ， m； 故答案为； 17如图，平面直角坐标系中，点 B 在第一象限，点 A 在 x 轴的正半轴上，AOBB 30，OA2，将AOB 绕点 O 逆时针旋转 90，点 B 的对应点 B的坐标是 （， 3） 【分析】 过点 B 和 B作 BDx 轴和 BCy 轴于点
26、 D、 C， 根据题意可得 B （3，） ， 进而可得点 B 的对应点 B的坐标 【解答】解：如图，过点 B 和 B作 BDx 轴和 BCy 轴于点 D、C， AOBB30， ABOA2，BAD60， AD1，BD， ODOA+AD3， B（3，） ， 将AOB 绕点 O 逆时针旋转 90，点 B 的对应点 B， BCBD，OCAD3， B坐标为： （，3） 故答案为： （，3） 18如图，直线 l：yx+1 分别交 x 轴、y 轴于点 A 和点 A1，过点 A1作 A1B1l，交 x 轴于点 B1，过点 B1作 B1A2x 轴，交直线 l 于点 A2；过点 A2作 A2B2l，交 x 轴于点
27、 B2，过点 B2作 B2A3x 轴，交直线 l 于点 A3，依此规律，若图中阴影A1OB1的面积 为 S1，阴影A2B1B2的面积为 S2，阴影A3B2B3的面积为 S3，则 Sn 【分析】由直线 l：yx+1 可求出与 x 轴交点 A 的坐标，与 y 轴交点 A1的坐标，进 而得到 OA，OA1的长，也可求出 RtOAA1的各个内角的度数，是一个特殊的直角三角 形， 以下所作的三角形都是含有 30角的直角三角形， 然后这个求出 S1、 S2、 S3、 S4、 根据规律得出 Sn 【解答】解：直线 l：yx+1，当 x0 时，y1；当 y0 时，x A（，0）A1（0，1） OAA130 又
28、A1B1l， OA1B130， 在 RtOA1B1中，OB1OA1， S1； 同理可求出：A2B1，B1B2， S2； 依次可求出：S3；S4；S5 因此：Sn 故答案为： 三解答题（共三解答题（共 7 小题）小题） 19 （1）计算： （1）2019+tan60+（3.14）0 （2）解不等式组，并求此不等式组的整数解 【分析】 （1）根据有理数的乘方、零指数幂和特殊角的三角函数值可以解答本题； （2）根据解一元一次不等式组的方法可以求得该不等式组的解集，从而可以得到它的整 数解 【解答】解： （1） （1）2019+tan60+（3.14）0 （1）2+1 ； （2）， 由不等式，得 x，
29、 由不等式，得 x4， 故原不等式组的解集是x4， 原不等式组的整数解是 1，2，3 20 齐齐哈尔市教育局想知道某校学生对扎龙自然保护区的了解程度， 在该校随机抽取了部 分学生进行问卷， 问卷有以下四个选项： A 十分了解； B 了解较多： C 了解较少： D 不 了解（要求：每名被调查的学生必选且只能选择一项） 现将调查的结果绘制成两幅不完 整的统计图请根据两幅统计图中的信息回答下列问题： （1）本次被抽取的学生共有 100 名； （2）请补全条形图； （3）扇形图中的选项“C了解较少”部分所占扇形的圆心角的大小为 108 ； （4） 若该校共有 2000 名学生， 请你根据上述调查结果估
30、计该校对于扎龙自然保护区 “十 分了解”和“了解较多”的学生共有多少名？ 【分析】 （1）本次被抽取的学生共 3030%100（名） ； （2）10020301040（名） ，据此补全； （3）扇形图中的选项“C了解较少”部分所占扇形的圆心角 36030%108； （4） 该校对于扎龙自然保护区 “十分了解” 和 “了解较多” 的学生： 20001200 （名） 【解答】解： （1）本次被抽取的学生共 3030%100（名） ， 故答案为 100； （2）10020301040（名） ， 补全条形图如下： （3）扇形图中的选项“C了解较少”部分所占扇形的圆心角 36030%108， 故答案为
31、108； （4）该校对于扎龙自然保护区“十分了解”和“了解较多”的学生： 20001200（名） ， 答：该校对于扎龙自然保护区“十分了解”和“了解较多”的学生共 1200 名 21 某网店专售一款电动牙刷， 其成本为 20 元/支， 销售中发现， 该商品每天的销售量 y （支） 与销售单价 x（元/支）之间存在如图所示的关系 （1）请求出 y 与 x 的函数关系式； （2）该款电动牙刷销售单价定为多少元时，每天销售利润最大？最大利润是多少元？ （3）近期武汉爆发了“新型冠状病毒”疫情，该网店店主决定从每天获得的利润中抽出 200 元捐赠给武汉， 为了保证捐款后每天剩余利润不低于 550 元，
32、 如何确定该款电动牙刷 的售单价？ 【分析】 （1）利用待定系数法求解可得； （2）设该款电动牙刷每天的销售利润为 w 元，根据“总利润每支的利润销售量”可 得函数解析式，配方成顶点式后利用二次函数的性质求解可得； （3）设捐款后每天剩余利润为 z 元，根据题意得出 z10x2+600x8000200 10x2+600x8200，求出 z550 时的 x 的值，再利用二次函数的图象和性质求解可得 【解答】解： （1）设 y 与 x 的函数关系式为 ykx+b， 将（30，100） ， （35，50）代入 ykx+b， 得， 解得， y 与 x 的函数关系式为 y10x+400； （2）设该款电
33、动牙刷每天的销售利润为 w 元， 由题意得 w（x20） y （x20） （10x+400） 10x2+600x8000 10（x30）2+1000， 100， 当 x30 时，w 有最大值，w 最大值为 1000 答： 该款电动牙刷销售单价定为 30 元时， 每天销售利润最大， 最大销售利润为 1000 元； （3）设捐款后每天剩余利润为 z 元， 由题意可得 z10x2+600x8000200 10x2+600x8200， 令 z550，即10x2+600x8200550， 10（x260x+900）250， x260x+90025， 解得 x125，x235， 画出每天剩余利润 z 关于
34、销售单价 x 的函数关系图象如解图， 由图象可得：当该款电动牙刷的销售单价每支不低于 25 元，且不高于 35 元时，可保证 捐款后每天剩余利润不低于 550 元 22如图，点 O 是线段 AH 上一点，AH3，以点 O 为圆心，OA 的长为半径作O，过点 H 作 AH 的垂线交O 于 C，N 两点，点 B 在线段 CN 的延长线上，连接 AB 交O 于点 M，以 AB，BC 为边作ABCD （1）求证：AD 是O 的切线； （2）若 OHAH，求四边形 AHCD 与O 重叠部分的面积； （3）若 NHAH，BN，连接 MN，求 OH 和 MN 的长 【分析】 （1）根据平行四边形的性质可知
35、ADBC，证明 OAAD，又因为 OA 为半径， 即可证明结论； （2） 利用锐角三角函数先求出OCH30， 再求出扇形 OAC 的面积， 最后求出OHC 的面积，两部分面积相加即为重叠部分面积； （3）设O 半径 OArOC，OH3r，在 RtOHC 中，利用勾股定理求出半径 r ，推出 OH，再在 RtABH 和 RtACH 中利用勾股定理分别求出 AB，AC 的长， 最后证BMNBCA，利用相似三角形对应边的比相等即可求出 MN 的长 【解答】解： （1）证明：四边形 ABCD 是平行四边形， ADBC， AHC90， HAD90，即 OAAD， 又OA 为半径， AD 是O 的切线；
36、（2）解：如右图，连接 OC， OHOA，AH3， OH1，OA2， 在 RtOHC 中，OHC90，OHOC， OCH30， AOCOHC+OCH120， S扇形OAC， CH， SOHC1， 四边形 ABCD 与O 重叠部分的面积S扇形OAC+SOHC+； （3）设O 半径 OArOC，OH3r， 在 RtOHC 中，OH2+HC2OC2， （3r）2+12r2， r，则 OH， 在 RtABH 中，AH3，BH+1，则 AB， 在 RtACH 中，AH3，CHNH1，得 AC， 在BMN 和BCA 中， BB，BMNBCA， BMNBCA， 即， MN， OH，MN 23某商店购进 A、
37、B 两种商品，购买 1 个 A 商品比购买 1 个 B 商品多花 10 元，并且花费 300 元购买 A 商品和花费 100 元购买 B 商品的数量相等 （1）求购买一个 A 商品和一个 B 商品各需要多少元； （2） 商店准备购买 A、 B 两种商品共 80 个， 若 A 商品的数量不少于 B 商品数量的 4 倍， 并且购买 A、 B 商品的总费用不低于 1000 元且不高于 1050 元， 那么商店有哪几种购买方 案？ 【分析】 （1）设购买一个 B 商品需要 x 元，则购买一个 A 商品需要（x+10）元，根据数 量总价单价结合花费 300 元购买 A 商品和花费 100 元购买 B 商
38、品的数量相等，即可 得出关于 x 的分式方程，解之经检验后即可得出结论； （2）设购买 B 商品 m 个，则购买 A 商品（80m）个，根据 A 商品的数量不少于 B 商 品数量的 4 倍并且购买 A、 B 商品的总费用不低于 1000 元且不高于 1050 元， 即可得出关 于 m 的一元一次不等式组， 解之即可得出 m 的取值范围， 再结合 m 为整数即可找出各购 买方案 【解答】解： （1）设购买一个 B 商品需要 x 元，则购买一个 A 商品需要（x+10）元， 依题意，得：， 解得：x5， 经检验，x5 是原方程的解，且符合题意， x+1015 答：购买一个 A 商品需要 15 元，
39、购买一个 B 商品需要 5 元 （2）设购买 B 商品 m 个，则购买 A 商品（80m）个， 依题意，得：， 解得：15m16 m 为整数， m15 或 16 商店有 2 种购买方案，方案：购进 A 商品 65 个、B 商品 15 个；方案：购进 A 商 品 64 个、B 商品 16 个 24如图 1，在矩形 ABCD 中，BC3，动点 P 从 B 出发，以每秒 1 个单位的速度，沿射线 BC 方向移动，作PAB 关于直线 PA 的对称PAB，设点 P 的运动时间为 t（s） （1）若 AB2 如图 2，当点 B落在 AC 上时，显然PAB是直角三角形，求此时 t 的值； 是否存在异于图 2
40、 的时刻，使得PCB是直角三角形？若存在，请直接写出所有符 合题意的 t 的值？若不存在，请说明理由 （2）当 P 点不与 C 点重合时，若直线 PB与直线 CD 相交于点 M，且当 t3 时存在某 一时刻有结论PAM45成立， 试探究： 对于 t3 的任意时刻， 结论 “PAM45” 是否总是成立？请说明理由 【分析】 （1）利用勾股定理求出 AC，由PCBACB，推出，即 可解决问题 分三种情形分别求解即可：如图 21 中，当PCB90时如图 22 中，当 PCB90时如图 23 中，当CPB90时 （2）如图 32 中，首先证明四边形 ABCD 是正方形，如图 32 中，利用全等三角形的
41、 性质，翻折不变性即可解决问题 【解答】解： （1）如图 1 中， 四边形 ABCD 是矩形， ABC90， AC， PCBACB，PBCABC90， PCBACB， ， ， PB24 tPB24 如图 21 中，当PCB90时， 四边形 ABCD 是矩形， D90，ABCD2，ADBC3， DB， CBCDDB， 在 RtPCB中，BP2PC2+BC2， t2（）2+（3t）2， t2 如图 22 中，当PCB90时， 在 RtADB中，DB， CB3 在 RtPCB中则有：，解得 t6 如图 23 中，当CPB90时，易证四边形 ABP为正方形，易知 t2 综上所述，满足条件的 t 的值为
42、 2s 或 6s 或 2s （2）如图 31 中， PAM45 2+345，1+445 又翻折， 12，34， 又ADMABM，AMAM， AMDAMB（AAS） ， ADABAB， 即四边形 ABCD 是正方形， 如图，设APBx PAB90x， DAPx， 易证MDABAM（HL） ， BAMDAM， 翻折， PABPAB90x， DABPABDAP902x， DAMDAB45x， MAPDAM+PAD45 25如图，抛物线 yx2+bx+c 与直线 yx+3 分别相交于 A，B 两点，且此抛物线与 x 轴的一个交点为 C，连接 AC，BC已知 A（0，3） ，C（3，0） （1）求抛物线
43、的解析式； （2）在抛物线对称轴 l 上找一点 M，使|MBMC|的值最大，并求出这个最大值； （3）点 P 为 y 轴右侧抛物线上一动点，连接 PA，过点 P 作 PQPA 交 y 轴于点 Q，问： 是否存在点 P 使得以 A，P，Q 为顶点的三角形与ABC 相似？若存在，请求出所有符合 条件的点 P 的坐标；若不存在，请说明理由 【分析】 （1）将 A（0，3） ，C（3，0）代入 yx2+bx+c，即可求解； （2）分当点 B、C、M 三点不共线时、当点 B、C、M 三点共线时，两种情况分别求解即 可； （3）分当时、当时两种情况，分别求解即可 【解答】解： （1）将 A（0，3） ，C
44、（3，0）代入 yx2+bx+c 得： ，解得：， 抛物线的解析式是 yx2+x+3； （2）将直线 yx+3 表达式与二次函数表达式联立并解得：x0 或4， A （0，3） ，B（4，1） 当点 B、C、M 三点不共线时， |MBMC|BC 当点 B、C、M 三点共线时， |MBMC|BC 当点 B、C、M 三点共线时，|MBMC|取最大值，即为 BC 的长， 如图1， 过点B作BEx轴于点E， 在RtBEC中， 由勾股定理得BC， |MBMC|取最大值为； （3）存在点 P 使得以 A、P、Q 为顶点的三角形与ABC 相似 设点 P 坐标为（x，x2+x+3） （x0） 在 RtBEC 中，BECE1，BCE45， 在 RtACO 中，AOCO3，ACO45， ACB180454590，AC3， 如图 2，过点 P 作 PQPA 交 y 轴于点 Q，则APQ90， 过点 P 作 PGy 轴于点 G，PGAAPQ90 PAGQAP，PGAQPA PGAACB90 当时， PAGBAC， ， 解得 x11，x20， （舍去） 点 P 的纵坐标为12+1+36， 点 P 为（1，6） ； 当时， PAGABC， 3， 解得 x1（舍去） ，x20（舍去） ， 此时无符合条件的
