1、九年级数学试题第 1 页 共 8 页 20192020学年度学年度第第二二学期学期阶段阶段教学教学质量质量检测题检测题 九年级数学九年级数学 （考试时间：90 分钟；满分：120 分） 说明： 1本试题分第卷和第卷两部分，共 23 题第卷为选择题，共 8 小题，24 分； 第卷为填空题、作图题、解答题，共 15 小题，96 分 2所有题目均在答题卡 上作答，在试题上作答无效 第卷（共 24 分） 一、选择题（本大题共 8 小题，每小题 3 分，共 24 分） 在每小题给出的四个选项中，只有一项是符合题目要求的 1 11 7 的绝对值是（） A 11 7 B 7 11 C11 7 D 7 11
2、2根据中国卫生健康委员会报道，截止到 2020 年 4 月 10 日 24 时，新型冠状病毒 肺炎疫情据 31 个省（自治区、直辖市）和新疆生产建设兵团报告，累计治愈出 院病例 77525 例，将 77525 用科学计数法表示为（） A 3 77.525 10B 4 7.7525 10C 5 0.77525 10D 5 7.7525 10 3下列图案中是轴对称图形，但不是中心对称图形的有（） ABCD 4下列运算正确的是（） A 325 aaaB 1 11 22 a a C 632 aaaD 2 122aaa 九年级数学试题第 2 页 共 8 页 （第 7 题）（第 5 题） （第 6 题）
3、B （第 8 题） 5如图，点 A，B，C 在O上，BO 的延长线交 AC 于点 D，A=40，C=25， 则ADB 的度数为（） A110B115C120D125 6如图，在平面直角坐标系中，线段 AB 的两个端点都在格点上，如果先将线段 AB 向右平移两个单位，得到线段 AB，其中点 A、B 的对应点分别为点 A、B，然 后将线段 AB绕点 P 顺时针旋转得到线段 AB，其中点 A、B的对应点分别为 点 A、B，则旋转中心点 P 的坐标为（） A（1,0）B（0,2）C（3,1）D（4，-1） 7如图，在ABC 中，点 D 是ABC 的内心，连接 DB，DC，过点 D 作 EFBC 分别交
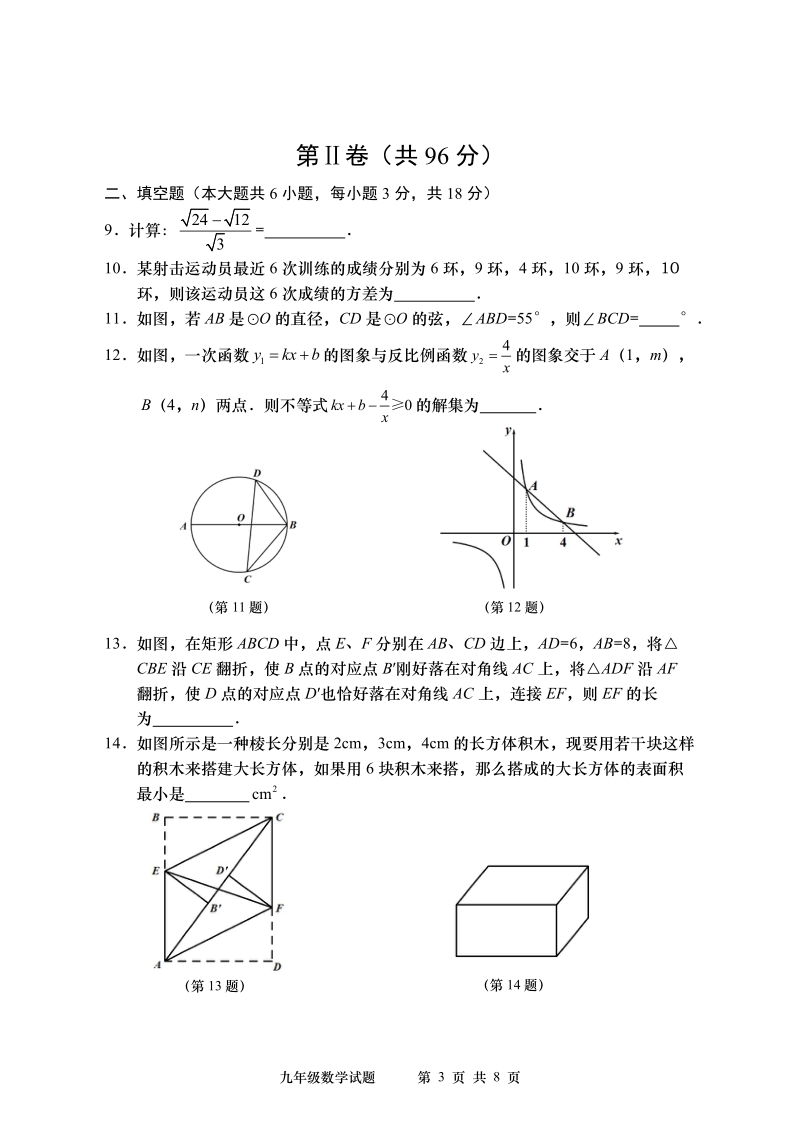
4、 AB、AC 于点 E、F，若 BE+CF=8，则 EF 的长度为（） A4B5C8D16 8已知二次函数 2 yaxbxc的图象如图，则一次函数 yaxbc与反比例函数 abc y x 在平面直角坐标系中的图 象可能是（） ADC 九年级数学试题第 3 页 共 8 页 （第 12 题） （第 13 题） 第卷（共 96 分） 二、填空题（本大题共 6 小题，每小题 3 分，共 18 分） 9计算： 2412 3 = 10某射击运动员最近 6 次训练的成绩分别为 6 环，9 环，4 环，10 环，9 环，10 环，则该运动员这 6 次成绩的方差为 11如图，若 AB 是O的直径，CD 是O的弦
5、，ABD=55，则BCD= 12如图，一次函数 1 ykxb的图象与反比例函数 2 4 y x 的图象交于 A（1，m）， B（4，n）两点则不等式 4 0kxb x 的解集为 13如图，在矩形 ABCD 中，点 E、F 分别在 AB、CD 边上，AD=6，AB=8，将 CBE 沿 CE 翻折，使 B 点的对应点 B刚好落在对角线 AC 上，将ADF 沿 AF 翻折，使 D 点的对应点 D也恰好落在对角线 AC 上，连接 EF，则 EF 的长 为 14如图所示是一种棱长分别是 2cm，3cm，4cm 的长方体积木，现要用若干块这样 的积木来搭建大长方体，如果用 6 块积木来搭，那么搭成的大长方
6、体的表面积 最小是 2 cm （第 11 题） （第 14 题） 九年级数学试题第 4 页 共 8 页 三、作图题（本大题满分 6 分） 请用直尺、圆规作图，不写作法，但要保留作图痕迹 15已知：，线段 c 求作：Rt ABC，使A ，AB=c，C=90 四、解答题（本大题共 8 小题，共 72 分） 16（本题每小题 5 分，共 10 分） （1） 2 31 1 442 a aaa （2）解不等式组 335 121 32 xx x x 17（本小题满分 6 分） 小明和小亮进行摸牌游戏，如图，他们有四张除牌面数字不同外、其他地方完 全相同的纸牌，牌面数字分别为 4，5，6，7，他们把纸牌背面
7、朝上，充分洗匀后， 从这四张纸牌中摸出一张，记下数字放回后，再次重新洗匀，然后再摸出一张，再 次记下数字，将两次数字之和做为对比结果若两次数字之和大于 11，则小明胜； 若两次数字之和小于 11，则小亮胜 （1）请你用列表法或树状图列出这个摸牌游戏中所有可能出现的结果 （2）这个游戏公平吗？请说明理由 九年级数学试题第 5 页 共 8 页 18（本小题满分 6 分） “停课不停学，学习不延期”，某市通过教育资源公共服务平台和有线电视为 全市中小学开设在线“空中课堂”，为了解学生每天的学习时间情况，在全市随机 抽取了部分初中学生进行问卷调查，现将调查结果绘制成如下不完整的统计图表， 请根据图表中
8、的信息解答下列问题： 组别学习时间 x（h）人数（人） A2.5x340 B3x3.5170 C3.5x4350 D4x4.5 E4.5x590 F5 小时以上50 （1）这次参与问卷调查的初中学生有人，中位数落在组 （2）补全条形统计图 （3）若此市有初中学生 2.8 万人，求每天参与“空中课堂”学习时间 3.5 到 4.5 小 时（不包括 3.5 小时）的初中学生有多少人？ （第 18 题） 九年级数学试题第 6 页 共 8 页 19（本小题满分 8 分） 为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树 活动如图，在一个坡度（或坡比）i1:2.4 的山坡 AB 上发现
9、有一棵古树 CD测 得古树底端 C 到山脚点 A 的距离 AC26 米，在距山脚点 A 水平距离 6 米的点 E 处， 测得古树顶端 D 的仰角AED48（古树 CD 与山坡 AB 的剖面、点 E 在同一平 面上，古树 CD 与直线 AE 垂直），则古树 CD 的高度约为多少米？ （参考数据：sin480.73，cos480.67，tan481.11） 20（本小题满分 10 分） 某市地铁 1 号线全长约 60km，市政府通过招标，甲、乙两家地铁工程公司承担 了施工任务，根据招标合同可知，甲公司每月计划施工效率是乙公司的 1.2 倍，则 乙公司单独施工比甲公司单独施工多用 10 个月，且市政
10、府需要支付给甲公司的施工 费用为 6 亿元/km，乙公司的施工费用为 5 亿元/km （1）甲、乙两家地铁工程公司每月计划施工各为多少 km？ （2）由于设备和施工现场只能供一家地铁工程公司单独施工的原因，现计划甲、 乙两家公司共用 55 个月恰好完成施工任务（每家公司施工时间不足一个月按照一个 整月计算），且甲公司施工时间不得少于乙公司的两倍，应如何安排才能使市政府 支付给两家地铁工程公司的总费用最少？ （第 19 题） 九年级数学试题第 7 页 共 8 页 21（本小题满分 10 分） 如图，在ABCD 中，点 E 是对角线 BD 上的一点，过点 C 作 CFBD，且 CF=DE，连接 A
11、E、BF、EF （1）求证：ADEBCF； （2）若BFCABE=90，判断四边形 ABFE 的形状，并证明你的结论 22（本小题满分 10 分） 某商场销售某种型号防护面罩，进货价为 40 元/个经市场销售发现：售价为 50 元/个时，每周可以售出 100 个，若每涨价 1 元，就会少售出 5 个供货厂家规 定市场售价不得低于 50 元/个，且商场每周销售数量不得少于 80 个 （1）确定商场每周销售这种型号防护面罩所得的利润 w（元）与售价 x（元/个） 之间的函数关系式 （2）当售价 x（元/个）定为多少时，商场每周销售这种防护面罩所得的利润 w （元）最大？最大利润是多少？ （第 21
12、 题） 九年级数学试题第 8 页 共 8 页 23（本小题满分 12 分） 如图，已知菱形 ABCD 中，对角线 AC、BD 相交于点 O，且 AC=12cm， BD=16cm，点 P 从点 D 出发，沿 DA 方向匀速向点 A 运动，速度为 2cm/s；同时， 点 E 从点 B 出发，沿 BO 方向匀速向点 O 运动，速度为 1cm/s，EFBC，交 OC 于 点 F当点 P、E 中有一点停止运动时，另一点也停止运动，线段 EF 也停止运动， 连接 PE、DF（0t5）解答下列问题： （1）当 t 为何值时，PEAB？ （2）设四边形 EFDP 的面积为 y（ 2 cm），求 y 与 t 之
13、间的函数关系式 （3）是否存在某一时刻 t，使得:21:48 EFDPABCD SS 四边形菱形 ？若存在，求出 t 的 值；若不存在，请说明理由 （4）连接 FP，是否存在某一时刻 t，使得 FPAD？若存在，求出 t 的值；若 不存在，请说明理由 （备用图）（第 23 题） 1 20192020学年度学年度第二学期阶段教学质量检测题第二学期阶段教学质量检测题 九年级数学参考答案九年级数学参考答案 一、选择题（本大题共 8 小题，每小题 3 分，共 24 分） 题号12345678 答案CBABDBCC 二、填空题（本大题共 6 小题，每小题 3 分，共 18 分） 三、作图题（本大题满分
14、6 分） 请用直尺、圆规作图，不写作法，但要保留作图痕迹 15作A 2 分 在A一边上作线段AB=c3 分 过 B 点作A另一边的垂线，交于点 C5 分 结论 6 分 四、解答题（本大题共 8 小题，共 72 分） 16解方程（本题每小题 5 分，共 10 分） （1） 222 31321321 1= 44244232 2 aaaaa aaaaaaaa a 5 分 （2）解：解不等式，得x2，2 分 解不等式，得 1 2 x ，4 分 因此，原不等式组的解集为 1 2 2 x ，5 分 17. （本小题满分 6 分） 解：（1） 2 分 （2）这个游戏是公平的3 分 题号91011121314
15、 答案 2 22 535 0x ， 14x 2 10 168 小亮 小明和 4567 4891011 59101112 610111213 711121314 2 总共有 16 种结果，每种结果出现的可能性是相同的， 两次数字之和大于 11 的结果有 6 种， 所以，P（小明获胜） 63 = 168 ，4 分 两次数字之和小于 11 的结果有 6 种， 所以，P（小亮获胜） 63 = 168 ，5 分 因为， 33 = 88 ， 所以，这个游戏是公平的6 分 18.（本小题满分 6 分） （1）解：1000C2 分 （2）1000-40-170-350-90-50=300（人）3 分 补全条形
16、统计图 4 分 （3）2.8 万人=28000 人 350300 28000=18200 1000 人6 分 19. （本小题满分 8 分） 解：延长 DC 交 EA 的延长线于点 F，则 CFEF1 分 山坡 AC 上坡度i1:2.4， 令 CFk，则 AF2.4k， 在 RtACF 中，由勾股定理得， CF2+AF2=AC2 k2(2.4k)2262， 解得 k10， AF24，CF10，3 分 EF304 分 在 RtDEF 中，tanE DF EF ， DFEFtanE30tan48301.1133.3，6 分 CDDFCF23.37 分 因此，古树 CD 的高度约为 23.3m8 分
17、 20. （本小题满分 10 分） 解：设乙公司每月计划施工 x km，则甲公司每月施工 1.2x km， 根据题意，得 6060 10 1.2xx 2 分 解得，x=13 分 经检验，x=1 是原方程的根，4 分 3 （第 21 题） 1.2x=1.21=1.2 因此，甲公司每月计划施工 1.2km，乙公司每月施工 1km5 分 （2）设甲公司施工了 m 个月，则乙公司施工（55-m）个月，共支付的总费用为 w 亿元，则 w=1.26m+15（55-m）=7.2m+275-5m=2.2m+2757 分 k=2.20，w 随着 m 的增大而增大，8 分 甲公司施工时间不得少于乙公司的两倍， 2
18、 55mm， 110 3 m， 当 m=37 时，w 有最大值， 55-37=18，9 分 因此，甲公司施工 37 个月，乙公司施工 18 个月，总费用最少10 分 21. （本小题满分 10 分） 证明：（1）四边形 ABCD 是平行四边形， AD=BC，ADBC，1 分 ADB=DBC， 又CFDB， DBC=BCF， ADB=BCF， 3 分 又DE=CF， ADEBCF； 4 分 （2）ABFE 是矩形6 分 CFDE，CF=DE 四边形 CDEF 是平行四边形， EFCD，EF=CD 四边形 ABCD 是平行四边形， ABCD，AB=CD ABEF，AB=EF 四边形 ABFE 是平
19、行四边形，8 分 ADEBCF， AED=BFC， 又BFCABE=90， AEDABE=90， AEDABE=BAE， BAE=90， ABFE 是矩形10 分 4 22. （本小题满分 10 分） 解：（1）根据题意，得 2 40100550403505555014000wxxxxxx ， 因此，利润与售价之间的函数关系式为 2 555014000wxx 4 分 （2）销售量不得少于 80 个， 100-5（x-50）80， x54， x50， 50x54，5 分 7 分 a=50，开口向下，对称轴为直线 x=55， 当 50x54 时，w 随着 x 的增大而增大，8 分 当 x=54 时
20、， w最大值= 2 5 54551125=1120， 因此，当售价定为 54 元时，每周获得的利润最大，最大利润为 1120 元10 分 23.（本小题满分 12 分） 解：（1）四边形 ABCD 是菱形， 11 126 cm 22 AOCOAC， 11 168 cm 22 BODOBD， ACBD，AB=BC=CD=DA， 在 RtAOD 中， 由勾股定理，得 222 AODOAD， 2222 6810 cmADAODO，1 分 PEAB， DEDP DBDA ，2 分 即， 162 1610 tt ， 80 21 t ， 因此，当 t 为 80 21 s 时，PEAB3 分 2 2 222
21、 2 555014000 =511014000 =5110555514000 =5551125 wxx xx xx x 5 （2）作 PQOD 于 Q， DQP=DOA=90， 又QDP=ODA， DQPDOA， PQDP AODA ， 即， 2 610 PQt ， 6 5 t PQ ，4 分 EFBC， OEOF OBOC ， 即， 8 86 tOF ， 3 6 4 OFt，5 分 11 22 EFDEDPEFDP ySSSDE OFDE PQ 四边形 2 131693 1661648 2425405 tttttt 因此，y 与 t 之间的函数关系式为 2 93 48 405 ytt 6 分
22、 （3）假设存在 t，使得:21:48 EFDPABCD SS 四边形菱形 ， 21 48 EFDPABCD SS 四边形菱形 ， 即， 2 93211 48=1662 405482 tt ，7 分 2 3880=0tt，8 分 解得， 1 4t ， 2 20 3 t ，均不符合题意， 因此，不存在 t，使:21:48 EFDPABCD SS 四边形菱形 9 分 6 （4）假设存在 t，使得 FPAD 四边形 ABCD 是菱形 ACBD=90， AOD=90， FPAD APF=90， AOD=APF， OAD=PAF， AODAPF10 分 AD AF AO AP 11 分 3 6 4 OFt ，DP=2t AF=t 4 3 12，AP=102t 10 4 3 12 6 210 t t t= 31 56 因此，当 t= 31 56 时，FPAD12 分
