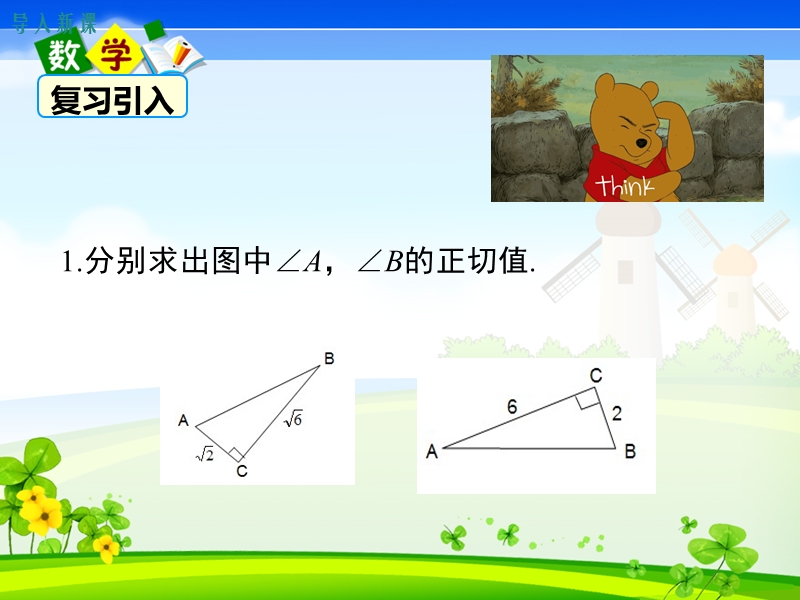
1、1.1 锐角三角函数,第一章 直角三角形的边 角关系,导入新课,讲授新课,当堂练习,课堂小结,第2课时 正弦与余弦,北师大版九年级下册数学教学课件,1.理解并掌握锐角正弦、余弦的定义，并进行相关计 算；（重点、难点） 2.在直角三角形中求正弦值、余弦值. (重点),学习目标,导入新课,复习引入,1.分别求出图中A，B的正切值.,2.如图，在RtABC中，C90，当锐角A确定时，A的对边与邻边的比就随之确定.想一想，此时，其他边之间的比是否也确定了呢？,任意画RtABC 和RtABC，使得CC90，AA，那么 与 有什么关系你能试着分析一下吗？,讲授新课,合作探究,在图中，由于CC90，AA，所
2、以ABCABC,这就是说，在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，A的对边与斜边的比也是一个固定值,A的对边与斜边的比叫做A的正弦（sine），记作sinA ， 即,c,a,b,对边,斜边,概念学习,典例精析,例1 如图，在RtABC中，B=90，AC=200，sinA=0.6，求BC的长.,解： 在RtABC中，,即, BC=2000.6=120.,变式：在RtABC中,C=90,BC=20, 求:ABC的周长和面积.,解: 在RtABC中,合作探究,任意画RtABC 和RtABC，使得CC90，AA，那么 与 有什么关系你能试着分析一下吗？,在图中，由于CC90，AA，
3、所以ABCABC,这就是说，在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，A的邻边与斜边的比也是一个固定值,A的邻边与斜边的比叫做A的余弦（cosine），记作cosA，即,c,a,b,对边,斜边,概念学习,锐角A的正弦、余弦和正切都是A的三角函数（trigonometric function）.当锐角A变化时，相应的正弦、余弦和正切值也随之变化.,定义中应该注意的几个问题:,1.sinA,cosA是在直角三角形中定义的,A是锐角(注意数形结合,构造直角三角形). 2.sinA,cosA是一个完整的符号,分别表示A的正弦,余弦 (习惯省去“”号). 3.sinA,cosA 是一个
4、比值.注意比的顺序.且sinA,cosA均0,无单位. 4.sinA,cosA的大小只与A的大小有关,而与直角三角形的边长无关. 5.角相等,则其三角函数值相等；两锐角的三角函数值相等,则这两个锐角相等.,例2：如图:在等腰ABC中,AB=AC=5,BC=6. 求: sinB,cosB,tanB.,提示:过点A作ADBC于D.,如图，梯子的倾斜程度与sinA和cosA有关系吗？,A,sinA的值越大,梯子越 _ ; cosA的值越 _ ,梯子越陡.,陡,小,A,议一议,例3：在RtABC中,C=90,如图,已知AC=3,AB=6, 求sinA和cosB.,想一想:我们发现sinA=cosB,其
5、中有没有什么内在的联系?,求:AB,sinB.,变式：如图:在RtABC中,C=90,AC=10,思考:我们再次发现sinA=cosB,其中的内在联系你可否掌握?,如图：在Rt ABC中，C90，,要点归纳,sinA=cosB,2.在RtABC中，C=90，sinA= ，则tanB的值为_.,针对训练,1.在RtABC中，C=90，则下列式子一定成立的是（ ） AsinA=sinB BcosA=cosB CtanA=tanB DsinA=cosB,D,1.如图,在RtABC中,锐角A的对边和邻边同时扩大100倍,sinA的值（ ） A.扩大100倍 B.缩小100倍 C.不变 D.不能确定,2
6、.已知A,B为锐角 (1)若A=B,则sinA sinB; (2)若sinA=sinB,则A B.,C,=,=,当堂练习,3.如图, C=90CDAB.,4.在上图中,若BD=6,CD=12.则cosA=_.,( ) ( ) ( ),( ) ( ) ( ),CDBC,ACAB,ADAC,5.如图：P是边OA上一点，且P点的坐标为（3，4），则cos =_,tan =_.,3,4,P,A,6. 如图，在RtABC中，C90，AB =10，BC6，求sinA、cosA、tanA的值,解：,又,10,变式1：如图，在RtABC中，C90， cosA ，求sinA、tanA的值,解：,设AC=15k，
7、则AB=17k,变式2：如图，在RtABC中，C90，AC8，tanA ，求sinA、cosB的值,A,B,C,8,解：,7如图，在正方形ABCD中，M是AD的中点，BE=3AE，求sinECM.,解：设正方形ABCD的边长为4x，M是AD的中点，BE=3AE， AMDM2x,AEx,BE3x 由勾股定理可知，,7如图，在正方形ABCD中，M是AD的中点，BE=3AE，求sinECM.,由勾股定理逆定理可知，EMC为直角三角形.,8如图，在平面直角坐标系内，O为原点，点A的坐标为(10，0)，点B在第一象限内，BO=5，sinBOA,(1)求点B的坐标； (2)求cosBAO的值,A,B,H,
8、解：(1)如图所示，作BHOA， 垂足为H在RtOHB中， BO5，sinBOA ,BH=3，OH4，,点B的坐标为(4，3),8如图，在平面直角坐标系内，O为原点，点A的坐标为(10，0)，点B在第一象限内，BO=5，sinBOA,(2)求cosBAO的值,A,B,H,(2)OA10，OH4， AH6 在RtAHB中，BH=3，,1.在RtABC中,课堂小结,2.梯子的倾斜程度与sinA和cosA的关系：,sinA的值越大,梯子越陡; cosA的值越小,梯子越陡.,“部编本”语文教材解读 “部编本”语文教材的编写背景。 （一）教材要体现国家意识、主流意识形态、党的认同，体现立德树人从娃娃抓起
9、。 （二）体现核心素养，中国学生发展核心素养包括社会责任，国家认同、国际理解、人文底蕴、科学精神、审美情趣、学会学习、身心健康、实践创新。 （三）语文、道德与法制、历史三个学科教材统编是大趋势。 （四）“一标多本”教材质量参差不齐，“部编本”力图起到示范作用。 二、“部编本”教材的编写理念： （一）体现核心价值观，做到“整体规划，有机渗透”。 （二）接地气，满足一线需要，对教学弊病起纠偏作用。提倡全民阅读，注重两个延伸：往课外阅读延伸，往语文生活延伸。 （三）加强了教材编写的科学性，编研结合。 （四）贴近当代学生生活，体现时代性。 “部编本”语文教材的七个创新点： （一）选文创新：课文总数减少，减少汉语拼音的难度。 （二）单元结构创新更加灵活的单元结构体制，综合性更强。 （三）重视语文核心素养，重建语文知识体系。 （四）三位一体，区分不同课型。“教读”、“自读”和“课外阅读”三位一体，整体提高学生的语文素养。 （五）把课外阅读纳入教材体制。 （六）识字写字教学更加讲究科学性。 （七）提高写作教学的效果。 新教材注重了六个意识。 、国家意识。 、目标意识。 、文体意识，非常突出文学素养的培养。 、读书意识。 、主体意识。 、科研意识。 小结：好教，但教好不易。,下课啦！,
