1、初初 2020 级初三（下）级初三（下）“五一五一”自主拓展数学试卷自主拓展数学试卷 考生须知： 1 本试卷满分 120 分，考试时间为 120 分钟. 2 答题前，考生先将自己的“姓名” 、 “考号” 、 “考场” 、 “座位号”在答题卡上填写清楚，将“条形码”准 确粘贴在条形码区域内. 3 请按照题号顺序在答题卡各题目的区域内作答，超出答题区域的答案无效；在草稿纸上、试题纸上答案 无效. 4 选择题必须使用 2B 铅笔填涂；非选择题必须使用 0.5 毫米黑色字迹的签字笔书写，字体工整、笔迹清 楚. 5 保持卡面整洁，不要折叠、不要弄脏、弄皱，不准使用涂改液、刮纸刀. 一、一、选择题： （本
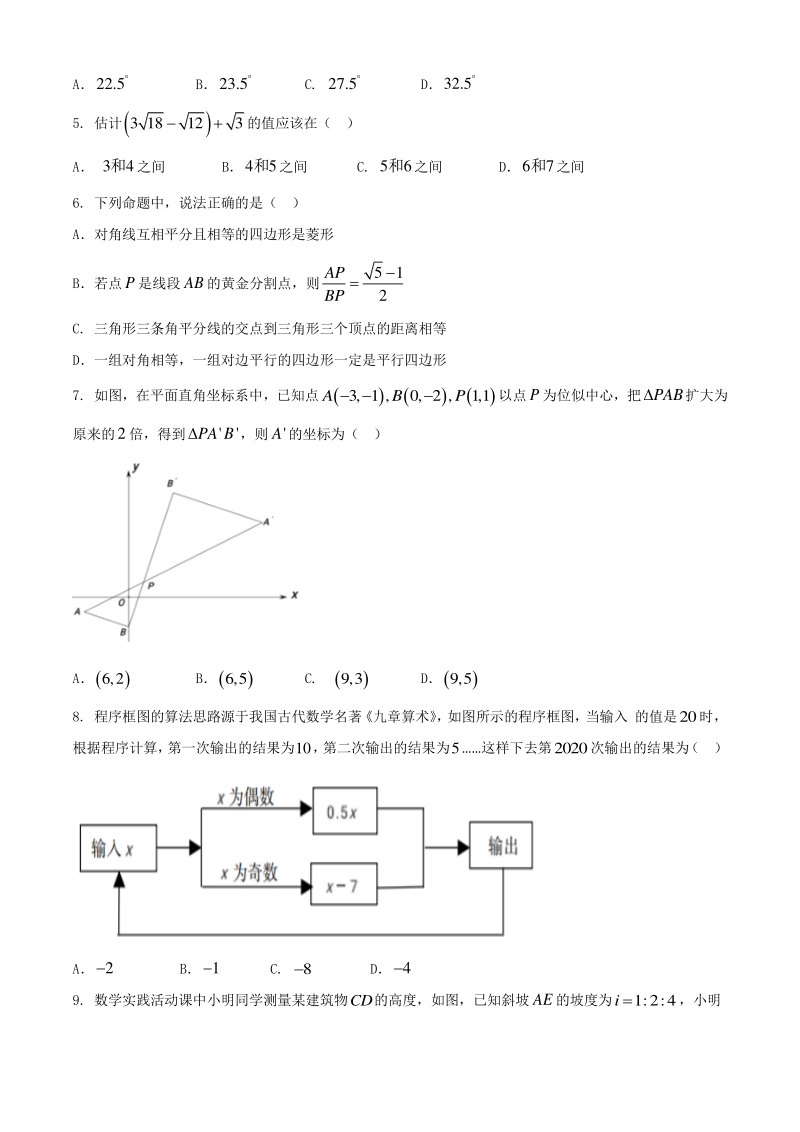
2、大题选择题： （本大题 12 个小题，每小题个小题，每小题 4 分，共分，共 48 分）在每个小题的下面，都给出了代分）在每个小题的下面，都给出了代 号为号为 A、B、C、 D 的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所 对应的方框涂黑对应的方框涂黑 1. 下列数是无理数的是（ ） A 1 2 B0 C3 D1 2. 下列各式中计算正确的是（ ） A 224 xxx B321xx C 2 2 24xx D 2 326 xyx y 3. 函数 21 x y x 的自变量x的取值范围是（ ） A 1 2 x B
3、1 2 x C 1 2 x D 1 0 2 xx 且 4. 如图，AB为O的切线，点B为切点，AO的延长线交O于点C，若35A ，则C的度数是 （ ） A22.5 B23.5 C. 27.5 D32.5 5. 估计 3 18123的值应该在（ ） A 34和之间 B45和之间 C. 56和之间 D67和之间 6. 下列命题中，说法正确的是（ ） A对角线互相平分且相等的四边形是菱形 B若点P是线段AB的黄金分割点，则 51 2 AP BP C. 三角形三条角平分线的交点到三角形三个顶点的距离相等 D一组对角相等，一组对边平行的四边形一定是平行四边形 7. 如图，在平面直角坐标系中，已知点3,
4、1 ,0, 2 ,1,1ABP 以点P为位似中心，把PAB扩大为 原来的2倍，得到PA B，则A的坐标为（ ） A6,2 B6,5 C. 9,3 D9,5 8. 程序框图的算法思路源于我国古代数学名著 九章算术 ， 如图所示的程序框图， 当输入 的值是20时， 根据程序计算， 第一次输出的结果为10， 第二次输出的结果为5这样下去第2020次输出的结果为 （ ） A2 B1 C. 8 D4 9. 数学实践活动课中小明同学测量某建筑物CD的高度，如图，已知斜坡AE的坡度为1:2:4i ，小明 在坡底点E处测得建筑物顶端C处的仰角为45，他沿着斜坡行走13米到达点F处，在F测得建筑 物顶 端C处的
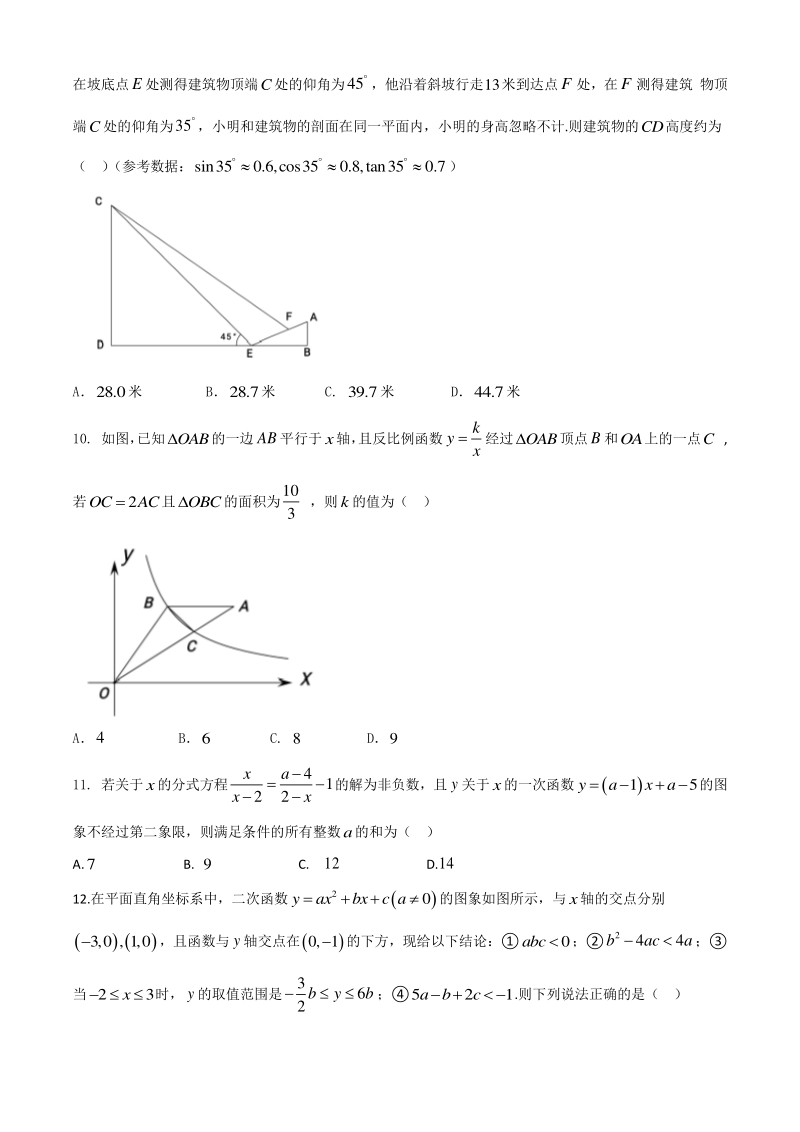
5、仰角为35，小明和建筑物的剖面在同一平面内，小明的身高忽略不计.则建筑物的CD高度约为 （ ） （参考数据：sin350.6,cos350.8,tan350.7 ） A28.0米 B28.7米 C. 39.7米 D44.7米 10. 如图， 已知OAB的一边AB平行于x轴， 且反比例函数 k y x 经过OAB顶点B和OA上的一点C , 若2OCAC且OBC的面积为10 3 ，则k的值为（ ） A4 B6 C. 8 D9 11. 若关于x的分式方程 4 1 22 xa xx 的解为非负数，且y关于x的一次函数15yaxa的图 象不经过第二象限，则满足条件的所有整数a的和为（ ） A.7 B.
6、9 C. 12 D.14 12.在平面直角坐标系中，二次函数 2 0yaxbxc a的图象如图所示，与x轴的交点分别 3,0 , 1,0 ，且函数与y轴交点在0, 1的下方，现给以下结论：0abc； 2 44baca； 当23x 时，y的取值范围是 3 6 2 byb；521abc .则下列说法正确的是（ ） A. B. C. D. 二、填空题： （本大题二、填空题： （本大题 6 6 个小题，每小题个小题，每小题 4 4 分，共分，共 2424 分）请将每小题的答案直接填在答题卡分）请将每小题的答案直接填在答题卡 对应的横线上对应的横线上 13.计算： 11 sin6032 2 14. 从1
7、 2 3 4、 、 、四个数中随机选取两个不同的数，分别记为, a c，则关于 的二次函数 2 4yaxxc的图 象与x轴无交点的概率为 15. 如图，正六边形ABCDEF的边长为3，分别以,A D为圆心，以,AB DC为半径作扇形BAF，扇形 CDE，则图中阴影部分的面积为 16. 如图在矩形ABCD中， 点E是线段AB上一点， 且满足513AEBE， 将AED沿ED所在直线翻 折， 点A恰好落在线段BC上点A处，连接AC交线段A D于点M ,若AB的长为9，则A MC的面积 为 17. 快慢两车分别从相距360千米的甲、 乙两地同时出发， 匀速行驶， 途中慢车因故障停留1小时， 然后 以
8、原速度的 4 3 倍继续向甲地行驶， 到达甲地后停止行驶； 快车匀速到达乙地后， 立即按原路原速返回甲 地 （快 车掉头时间忽略不计） ，并且比慢车提前15分钟到达甲地，快慢两车之间的距离y（千米）与快 车行驶时 间x（小时）之间的函数图象如图所示.则当两车第二次相遇时，两车距甲地还有 千米. 18. 如图，Rt ABC中，,6,4ABBC ABBC， 点D是ABC内一个动点,且满足DABDBC, 当CD线段AB取最小值时,记BCD,线段AB上一动点E绕着点D顺时针旋转得到点F,且满足 EDF ,则AF的最小值为 三、解答题： （本大题共三、解答题： （本大题共 8 8 个小题，个小题，191
9、9 题题 8 8 分，分，20202626 每题每题 1010 分，共分，共 7878 分）解答时每小分）解答时每小 题都必须写出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上题都必须写出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上21. 19. 1 ）因式分解 3 16a bab 2化简： 2 2 132 2 22 aa a aaa 20.如图，在ABC中，点D、点E分别为,AC BC上的两点，连接,BD DE,使得，,BDBC DE平分 BDC,且 . 1求证：ADBC ; 2若 117BED ,求A的度数. 21.受到“新型肺炎”影响，全国中小学未能
10、按时开学，为响应国家“停课不停学”的号召，重庆某重点中学组 织全校师生开展线上教学活动，体育备课组也为同学们提出了每日锻炼建议。疫情过去开学后，体育组彭 老师为检测同学们在家锻炼情况，在甲、乙两班同学中各随机抽取20名学生进行检测，并对数据进行了整 理、分析.下面给出了部分信息: 甲班:33,35,38,39,39,41,42,43,43,44,45,46,46,47,48,49,49,49,50,50 乙班成绩在4045x中的数据是41,43,41,44,42,40,43 整理数据： 成绩 班级 3050x 3540x 4045x 4550x 甲 1 4 a 10 乙 1 3 7 9 分析数
11、据： 班级 平均数 中位数 众数 甲 43.7 44.5 b 乙 43.4 c 48 根据以上信息，回答下列问题： 1a b c 2根据以上数据，你认为哪个班级在家体育锻炼的效果比较好，请说明理由(1条理由即可). 3已知九年级共有2000名学生，请估计全年级体育成绩大于等于45分的学生有多少人？ 22.数学学习小组根据函数学习的经验，对一个新函数2 a yx x 的图象和性质进行了如下探究: 1列表,下表是函数y与自变量x的几组对应值 x 3 2 1 1 2 1 2 1 3 2 2 3 7 2 y 10 3 4 m 10 6 2 n 0 2 3 6 7 请直接写出a m n 2如图，在平面直
12、角系xOy中，描出上表中各对对应值为坐标的点 （其中x为横坐标，y为纵坐标） ， 并根据描出的点画出函数的图象 3观察所画出的函数图象，写出该函数的性质（写一条性质即可） 4请结合画出的函数图象与表格中数据，直接写出关于x的不等式的解集： 242 a xx x 23.2019新型冠状病毒2019nCoV（），因2019年武汉出现的病 毒性肺炎病例而被发现，为防治疫情的 蔓延， 专家们建议大家出门都要佩戴口罩， 因此口罩的销售量 大增.某药店销售一种口罩， 经市场调查发现： 2020 年 2 月以100元/盒的进价购进一款口罩2000盒， 以150元/盒的售价迅速销售完3 月我国疫情得 到控制,
13、多家爱心企业也转产该款口罩，所以口罩的储 备量迅速上升，销售人员根据市场调研发现，该款口 罩每盒的售价在 2 月售价基础上每降价5元，月 销量就会相应增加100盒 1若该药店 3 月计划销售该款口罩不超过2600盒，则该款口罩 3 月的售价每盒至少多少元？ 2实际上，3 月该药店购进该款口罩的进价比 2 月便宜了 % 2 m ，而实际售价在 2 月基础上降了m元，且 购进的口罩全部销售完，已知该款口罩 3 月的销售利润比 2 月减少% 5 m ，求m的值 24如图:已知抛物线 2 yaxbxc与x轴，y轴分别交于点1,0 , ,0, 5AB C，此抛物线的对称轴 为直线2x . 1求出此抛物线
14、的解析式； 2如图 1， 抛物线的顶点为点D， 点P是直线BC下方抛物线上的一点 （异于点D） ， 当 BOPBCD SS 时， 求出点P的坐标； 3在 2的条件下，将抛物线沿射线DC方向平移，点P的对应点为 P，在抛物线平移的过程中,若 P CBPBC，请直接写出此时平移后的抛物线解析式 25定义：在平面直角坐标系中，对于任意两点 1122 ,A x yB x y， ，当点,T x y满足 22 12 12 3 , 44 yy xx xy ， 时，则称点T为点,A B，的“四合点”例如：1,2 ,9,6AB，当点 ,T x y满足 22 3 26 1 9 2,10 3 44 xy ，则点 2
15、,10 3T为点,A B，的“四合点” 1若点1,2 ,5, 2AB ，则点,A B的“四合点” 的坐标为 2如图，点4,0C ，点 1 ,2 2 D tt 是直线l上一点,点,T x y为点,C D的“四合点”， 请求出y关于x的函数关系式； 已知点 2,2 3E,在直线2x 上是否存在点Q， 使得CTQ与OCE相似,若存在， 请求出D此时点 的坐标；若不存在，请说明理由 26.(8 分)在平行四边形ABCD中，已知45 ,AADBD ，点E为线段 上的一点，连接DE， 以线段 DE为直角边构造等腰,Rt DEF EF， 交线段AB于点G，连接 . 1如图 1，若 12 2,5ABBE，则D
16、E的长为多少? 2如图 2，若点 ,H K分别为线段,BG DE的中点，连接HK，求证：2AGHK； 3如图 3，在 2的条件下,若 2,2 2BEBG，以点G为圆心，AG为半径作G，点M为G上 一点，连接MK，取MK的中点P，连接AP，请直接写出线段AP的取值范围. 初初 20202020 级初三级初三( (下下) )“五一”自主拓展“五一”自主拓展 数学数学( (答案答案) ) 一、选择题一、选择题:(:(每小题每小题 4 4 分，共计分，共计 4848 分分) ) 1-5: CDACC 6-10: DDBDC 11-12：CC 二、填空题二、填空题：( (每小题每小题 4 4 分，共分，
17、共 2424 分分) ) 13. 13 3 24 14. 1 2 15. 27 36 2 16. 75 16 17.45 18.12 5 三、解答题： （共三、解答题： （共 7878 分）分） 19. 1因式分解： 3 16a bab 解：原式44ab aa 2化简： 2 2 132 2 22 aa a aaa 解：原式 2 112 2 1 aaa a a a 1 1 a a a 20. 证明: 1DE平分 ADC BDECDE 又/DE AB BDEABDCDEA ADBDBC 2 BDBC 2BDCBCDA 3BEDCEDCA 39A 21. 1 5,49,43.5 ;abc 2里班体育
18、水平高一-些，因为甲班平均数43.7大于乙班平均数 43.4(中 109 3 2000950 40 （人） 答:全年级体育成绩大于等于45分的有950人。 22. 12a ，6m， 2 3 n 2如图，在平面直角系xOy中，描出上表中各对对应值为坐标的点(其中x为横坐标，y为纵坐标)，并根 据描出的点画出函数的图象; 3观察所画出的函数图像，写出该函数的性质（写一条性质即可） 当2x 时，y随x的增大而增大 ，当02x或0x时，y随x的增大减小 4101xx或 23. 解： 1设该款口罩 3月的定价为x元/盒，由题可列 150 2001002600 5 x 解得120x 答：该款口罩3月定价至
19、少为120元/盒。 2由题可列 150100 1%20001002000150 1001% 255 mmm m 2 200mm 解得 1 0m （舍） ， 2 20m 20m 24解 1由题抛物线对称轴为直线 2x 且过点1,0 ?0, 5AC（） 得 2 2 0 5 b a abc c ， 1 4 5 a b c 抛物线解析式为 2 45yxx 2由题抛物线的定点2, 9D 过点D作直线/DPBC交抛物线于点P 5,0 , 0, 5BC :5 BC lyx :5 DP lyx 则 2 11 45 yx yxx 解得： 1 1 2 9 x y （舍去） ， 2 2 3 8 x y 3, 8P
20、3新抛物线解析式为 2 2 115 4 24 yxyxx 或 2 2 117250 3339 yxyxx 25. 1若点1,2 ,5, 2AB， 则点,A B的“四合点” T的坐标为 1,2 3 2 点T为4,0C与点 1 ,2 2 D tt 的四合点 2 2 431 ,20 442 t xyt 44tx 23 442 4 yx 23 24 4 x 2 34 34 3xx 如图 2,2 3 ,4,0EC OEC为等边三角形 又CTQ与OCE相似 CTQ为等边三角形 ,60,COCEOCQTCETCO CQCT OQCETC OQET 又直线2x 垂直平分OC， 且点Q为直线 2x 上一点 OQ
21、QC OQQCTCTE OT垂直平分EC 直线 3 : 3 OT yx 令 2 3 34 34 3 3 xxx， 解得 12 4 3, 3 xx 12 4 4 3 3, 3, 39 TT 或 12 44 8,2, 33 DD 或 26.解： 145A ， 且ADBD ABD为等腰直角三角形 又12 2AB 12BD 在Rt BED中，有勾股定理得 22 13DEABBE 2过点G作GMAB 交AD延长线于M， 连接,KM GK 易证ABFBDE SAS（） 90DAFDBEAFBE ， 由AFGD、 、 、四点共圆得 180180DGFDAFADGAFG ， 90DGFDGFG ， 又ADG与GDM互补 GDMAFG 易证：AFGDGM ASA（） ADDMGMAG， 由此易证DMKBKE SAS（） K为MB中点 又HKAB且GM垂直AB /HKGM HK为GBM中位线 2GMHK 2AGHK 170170 32 22 2 22 AP
