1、2020 年广东省深圳市中考仿真模拟复习试卷年广东省深圳市中考仿真模拟复习试卷 一选择题（共一选择题（共 12 小题，满分小题，满分 36 分，每小题分，每小题 3 分）分） 1下列各数中，最小的数是（ ） A5 B3 C0 D2 2大家翘首以盼的长株潭城际铁路通车后，从长沙到株洲只需 24 分钟，从长沙到湘潭只需 25 分钟，这条铁路线全长 95500 米，则数据 95500 用科学记数法表示为（ ） A0.955105 B9.55105 C9.55104 D9.5104 3下列标志中，可以看作是轴对称图形的是（ ） A B C D 4如图是由几个大小相同的小正方体搭成的几何体的俯视图，小正
2、方形中的数字表示该位 置上小正方体的个数，则该几何体的左视图是（ ） A B C D 5不等式组的解集是（ ） Ax3 Bx3 Cx2 Dx2 6在一次中学生田径运动会上，参加男子跳高的 15 名运动员的成绩如下表所示： 成绩/m 1.50 1.60 1.65 1.70 1.75 1.80 人数 2 3 2 3 4 1 则这些运动员成绩的中位数、众数分别为（ ） A1.65、1.70 B1.65、1.75 C1.70、1.75 D1.70、1.70 7若一个三角形的两边长分别为 3 和 7，则第三边长可能是（ ） A6 B3 C2 D11 8在同一平面直角坐标系中，函数 ymx+m 与 y（m
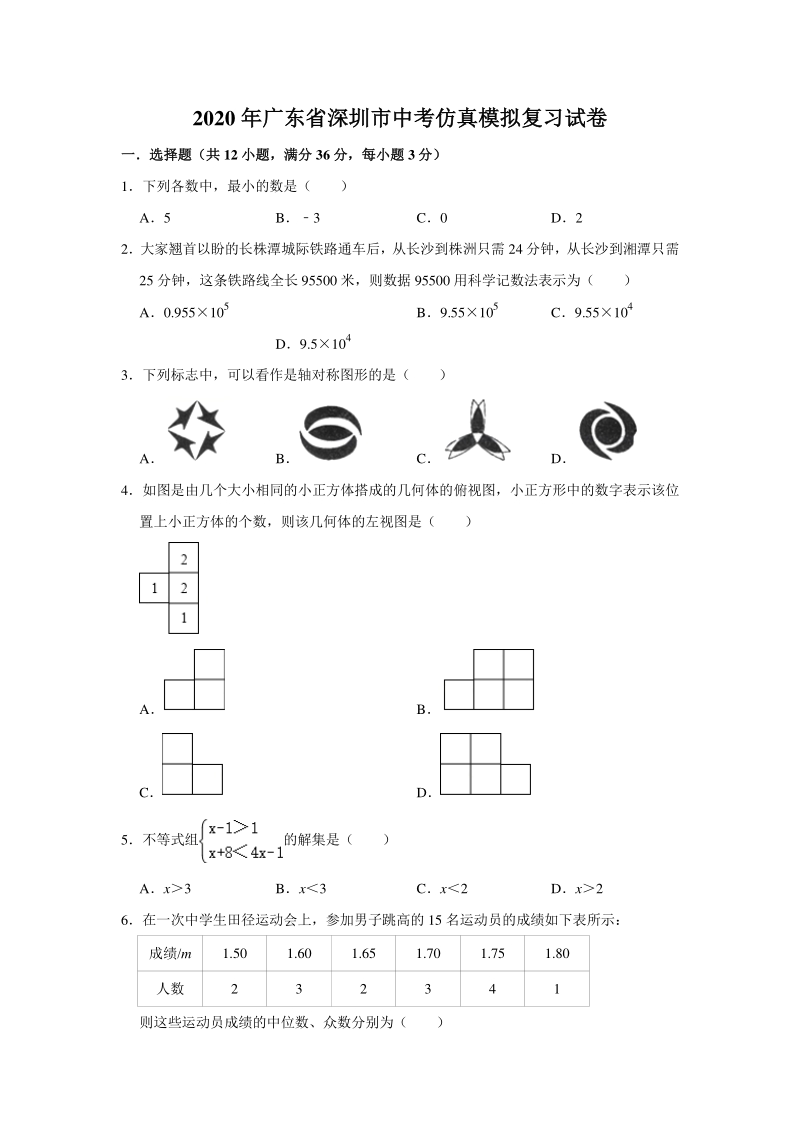
3、0）的图象可能是（ ） A B C D 9如图，ABCD，E 为 CD 上一点，射线 EF 经过点 A，ECEA若CAE30，则 BAF（ ） A30 B40 C50 D60 10如图是抛物线 yax2+bx+c（a0）的部分图象，其顶点坐标为（1，n） ，且与 x 轴的一 个交点在点（3，0）和（4，0）之间则下列结论： ab+c0； 3a+b0； b24a（cn） ； 一元二次方程 ax2+bx+cn1 有两个不相等的实数根 其中正确结论的个数是（ ） A1 B2 C3 D4 11如图，热气球的探测器显示，从热气球 A 处看一栋楼顶部 B 处的仰角为 30，看这栋 楼底部C处的俯角为60，
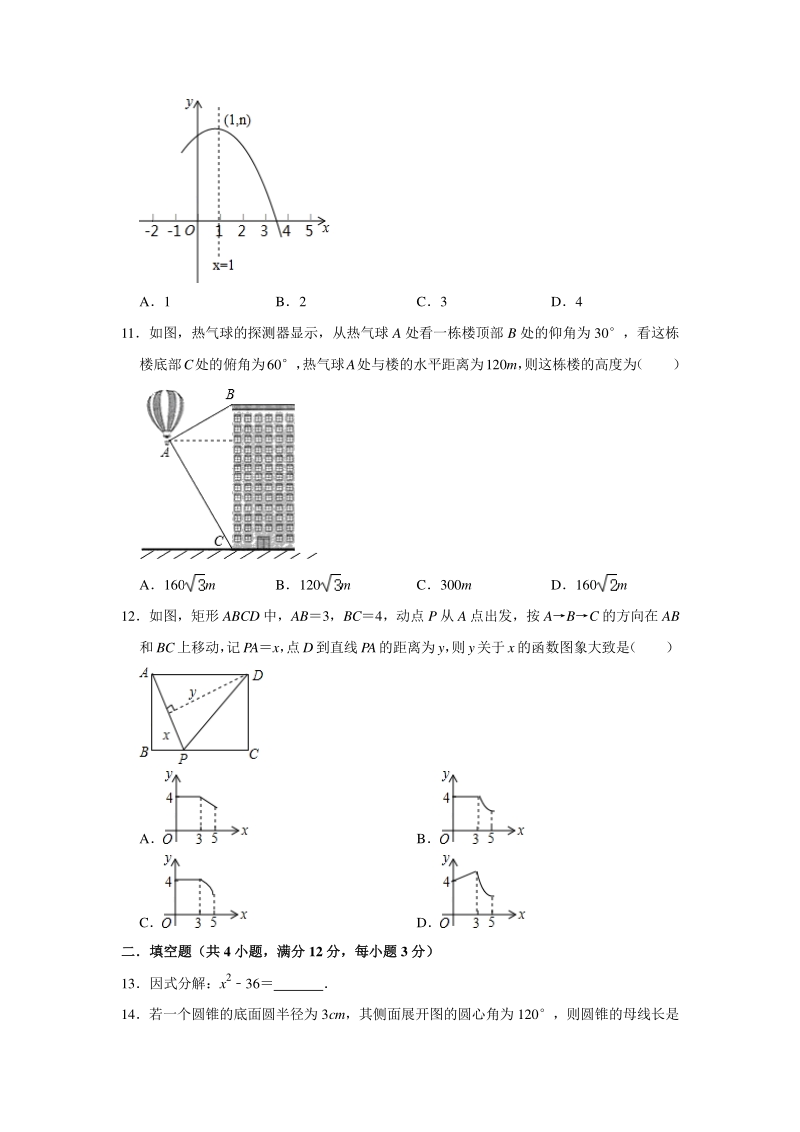
4、 热气球A处与楼的水平距离为120m， 则这栋楼的高度为 （ ） A160m B120m C300m D160m 12如图，矩形 ABCD 中，AB3，BC4，动点 P 从 A 点出发，按 ABC 的方向在 AB 和BC上移动， 记PAx， 点D到直线PA的距离为y， 则y关于x的函数图象大致是 （ ） A B C D 二填空题（共二填空题（共 4 小题，满分小题，满分 12 分，每小题分，每小题 3 分）分） 13因式分解：x236 14若一个圆锥的底面圆半径为 3cm，其侧面展开图的圆心角为 120，则圆锥的母线长是 cm 15 如图， 将边长为 6cm 的正方形 ABCD 折叠， 使点
5、D 落在 AB 边的中点 E 处， 折痕为 FH， 点 C 落在 Q 处，EQ 与 BC 交于点 G，则 BG 的长是 cm 16如图，直线 yx+2 与 x 轴交于 C，与 y 轴交于 D，以 CD 为边作矩形 CDAB，点 A 在 x 轴上，双曲线 y（k0）经过点 B 与直线 CD 交于 E，EMx 轴于 M，则 S四边形 BEMC 三解答题（共三解答题（共 7 小题，满分小题，满分 52 分）分） 17计算： 18先化简，再求值：，其中 x 的值从不等式组的整数 解中选取 19一个口袋中有 3 个大小相同的小球，球面上分别写有数字 1、2、3，从袋中随机地摸出 一个小球，记录下数字后放
6、回，再随机地摸出一个小球 （1）请用树形图或列表法中的一种，列举出两次摸出的球上数字的所有可能结果； （2）求两次摸出的球上的数字和为偶数的概率 20山地自行车越来越受到中学生的喜爱，各种品牌相继投放市场，某车行经营的 A 型车 去年销售总额为 5 万元，今年每辆销售价比去年降低 400 元，若卖出的数量相同，销售 总额将比去年减少 20% （1）今年 A 型车每辆售价多少元？（用列方程的方法解答） （2）该车行计划新进一批 A 型车和新款 B 型车共 60 辆，且 B 型车的进货数量不超过 A 型车数量的两倍，应如何进货才能使这批车获利最多？ A，B 两种型号车的进货和销售价格如下表： A
7、型车 B 型车 进货价格（元） 1100 1400 销售价格（元） 今年的销售价格 2000 21在线段 AB 的同侧作射线 AM 和 BN，若MAB 与NBA 的平分线分别交射线 BN，AM 于点 E，F，AE 和 BF 交于点 P如图，点点同学发现当射线 AM，BN 交于点 C；且 ACB60时，有以下两个结论： APB120；AF+BEAB 那么，当 AMBN 时： （1） 点点发现的结论还成立吗？若成立， 请给予证明； 若不成立， 请求出APB 的度数， 写出 AF，BE，AB 长度之间的等量关系，并给予证明； （2） 设点 Q 为线段 AE 上一点， QB5， 若 AF+BE16，
8、四边形 ABEF 的面积为 32， 求 AQ 的长 22如图，四边形 ABCD 内接于O，对角线 AC 为O 的直径，过点 C 作 AC 的垂线交 AD 的延长线于点 E，点 F 为 CE 的中点，连接 DB，DC，DF （1）求CDE 的度数； （2）求证：DF 是O 的切线； （3）若 AC2DE，求 tanABD 的值 23在平面直角坐标系中，已知抛物线 yx2+bx+c 的顶点 M 的坐标为（1，4） ，且与 x 轴交于点 A，点 B（点 A 在点 B 的左边） ，与 y 轴交于点 C （1）填空：b ，c ，直线 AC 的解析式为 ； （2）直线 xt 与 x 轴相交于点 H 当 t
9、3 时得到直线 AN（如图 1） ，点 D 为直线 AC 下方抛物线上一点，若COD MAN，求出此时点 D 的坐标； 当3t1 时（如图 2） ，直线 xt 与线段 AC，AM 和抛物线分别相交于点 E，F， P 试证明线段 HE， EF， FP 总能组成等腰三角形； 如果此等腰三角形底角的余弦值为， 求此时 t 的值 参考答案参考答案 一选择题（共一选择题（共 12 小题，满分小题，满分 36 分，每小题分，每小题 3 分）分） 1 【解答】解：3025， 则最小的数是3， 故选：B 2 【解答】解：955009.55104， 故选：C 3 【解答】解：A、是中心对称图形，故 A 错误；
10、B、是中心对称图形，故 B 错误； C、是轴对称图形，故 C 正确； D、是中心对称图形，故 D 错误； 故选：C 4 【解答】解：该几何体的左视图是： 故选：D 5 【解答】解：， 解得：x2， 解得：x3， 则不等式的解集是：x3 故选：A 6 【解答】解：共 15 名学生，中位数落在第 8 名学生处，第 8 名学生的跳高成绩为 1.70m， 故中位数为 1.70； 跳高成绩为 1.75m 的人数最多，故跳高成绩的众数为 1.75； 故选：C 7 【解答】解：设第三边为 x，则 4x10， 所以符合条件的整数为 6， 故选：A 8 【解答】解：A、由函数 ymx+m 的图象可知 m0，由函
11、数 y的图象可知 m0，故 A 选项正确； B、由函数 ymx+m 的图象可知 m0，由函数 y的图象可知 m0，相矛盾，故 B 选项错误； C、 由函数 ymx+m 的图象 y 随 x 的增大而减小， 则 m0， 而该直线与 y 轴交于正半轴， 则 m0，相矛盾，故 C 选项错误； D、 由函数 ymx+m 的图象 y 随 x 的增大而增大， 则 m0， 而该直线与 y 轴交于负半轴， 则 m0，相矛盾，故 D 选项错误； 故选：A 9 【解答】解：ECEACAE30， C30， AED30+3060 ABCD， BAFAED60 故选：D 10 【解答】解：抛物线与 x 轴的一个交点在点（
12、3，0）和（4，0）之间，而抛物线的对 称轴为直线 x1， 抛物线与 x 轴的另一个交点在点（2，0）和（1，0）之间 当 x1 时，y0， 即 ab+c0，所以正确； 抛物线的对称轴为直线 x1，即 b2a， 3a+b3a2aa，所以错误； 抛物线的顶点坐标为（1，n） ， n， b24ac4an4a（cn） ，所以正确； 抛物线与直线 yn 有一个公共点， 抛物线与直线 yn1 有 2 个公共点， 一元二次方程 ax2+bx+cn1 有两个不相等的实数根，所以正确 故选：C 11 【解答】解：过点 A 作 ADBC 于点 D，则BAD30，CAD60，AD120m， 在 RtABD 中，B
13、DADtan3012040（m） ， 在 RtACD 中，CDADtan60120120（m） ， BCBD+CD160（m） 故选：A 12 【解答】解：点 P 在 AB 上时，0x3，点 D 到 AP 的距离为 AD 的长度，是定值 4； 点 P 在 BC 上时，3x5， APB+BAP90， PAD+BAP90， APBPAD， 又BDEA90， ABPDEA， ， 即， y， 纵观各选项，只有 B 选项图形符合 故选：B 二填空题（共二填空题（共 4 小题，满分小题，满分 12 分，每小题分，每小题 3 分）分） 13 【解答】解：x236（x+6） （x6） 14 【解答】解：设母线
14、长为 l，则23 解得：l9 故答案为：9 15 【解答】解：正方形 ABCD 折叠点 D 落在 AB 边的中点 E 处， EFFD， 设 AFx，则 EF6x， 点 E 是 AB 的中点， AEBE63， 在 RtAEF 中，由勾股定理得，AE2+AF2EF2， 即 32+x2（6x）2， 解得 x， FEG90， AEF+BEG90， BEG+BGE90， AEFBGE， 又AB90， AEFBGE， ， BG4cm 故答案为：4 16 【解答】解：根据题意，直线 yx+2 与 x 轴交于 C，与 y 轴交于 D， 分别令 x0，y0， 得 y2，x4， 即 D（0，2） ，C（4，0）
15、， 即 DC2， 又 ADDC 且过点 D， 所以直线 AD 所在函数解析式为：y2x+2， 令 y0，得 x1， 即 A（1，0） ， 同理可得 B 点的坐标为 B（3，2） 又 B 为双曲线（k0）上， 代入得 k6 即双曲线的解析式为 与直线 DC 联立， ， 得和 根据题意，不合题意， 故点 E 的坐标为（6，1） 所以 BC，CE， CM2，EM1， 所以 SBECBCEC， SEMCEMCM1， 故 S四边形BEMCSBEC+SEMC 故答案为： 三解答题（共三解答题（共 7 小题，满分小题，满分 52 分）分） 17 【解答】解：原式23+19 13+19 10 18 【解答】解
16、： 1 （） ， 解不等式组得： 1x， 当 x2 时，原式2 19 【解答】解： （1）画树状图得： 则共有 9 种等可能的结果； （2）由（1）得：两次摸出的球上的数字和为偶数的有 5 种情况， 两次摸出的球上的数字和为偶数的概率为： 20 【解答】解： （1）设今年 A 型车每辆售价 x 元，则去年售价每辆为（x+400）元，由题 意，得 ， 解得：x1600 经检验，x1600 是原方程的根 答：今年 A 型车每辆售价 1600 元； （2）设今年新进 A 型车 a 辆，则 B 型车（60a）辆，获利 y 元，由题意，得 y（16001100）a+（20001400） （60a） ，
17、y100a+36000 B 型车的进货数量不超过 A 型车数量的两倍， 60a2a， a20 y100a+36000 k1000， y 随 a 的增大而减小 a20 时，y最大34000 元 B 型车的数量为：602040 辆 当新进 A 型车 20 辆，B 型车 40 辆时，这批车获利最大 21 【解答】解：点点的结论：ACB60， BAC+ABC120， MAB 与NBA 的平分线分别交射线 BN，AM 于点 E，F， PAB+PBA（PAB+PBA）60， APB120， 如图，在 AB 上取一点 G，使 AGAF， AE 是BAM 的角平分线， PAGPAF， 在PAG 和PAF 中，
18、 PAGPAF（SAS） ， AFPAGP， EPFAPB120，ACB60， EPF+ACB180， PFC+PEC180， PFC+AFP180， PECAFP， PECAGP， AGP+BGP180， PEC+BGP180， PEC+PEB180， BGPBEP， BF 是ABC 的角平分线， PBGPBE， 在BPG 和BPE 中， BPGBPE（AAS） ， BGBE， AF+BEAB （1）原命题不成立，新结论为：APB90，AF+BE2AB（或 AFBEAB） ， 理由：AMBN， MAB+NBA180， AE，BF 分别平分MAB，NBA， EABMAB，FBANBA， EAB
19、+FBA（MAB+NBA）90， APB90， AE 平分MAB， MAEBAE， AMBN， MAEBEA， BAEBEA， ABBE， 同理：AFAB， AF+BE2AB（或 AFBEAB） ； （2）如图 1， 过点 F 作 FGAB 于 G， AFBE，AFBE， 四边形 ABEF 是平行四边形， AF+BE16， ABAFBE8， 328FG， FG4， 在 RtFAG 中，AF8， FAG60， 当点 G 在线段 AB 上时，FAB60， 当点 G 在线段 BA 延长线时，FAB120， 如图 2， 当FAB60时，PAB30， PB4，PA4， BQ5，BPA90， PQ3， A
20、Q43 或 AQ4+3 如图 3， 当FAB120时，PAB60，FBG30， PB4， PB45， 线段 AE 上不存在符合条件的点 Q， 当FAB60时，AQ43 或 4+3 22 【解答】 （1）解：对角线 AC 为O 的直径， ADC90， EDC90； （2）证明：连接 DO， EDC90，F 是 EC 的中点， DFFC， FDCFCD， ODOC， OCDODC， OCF90， ODFODC+FDCOCD+DCF90， DF 是O 的切线； （3）解：方法一：设 DE1，则 AC2， 由 AC2ADAE 20AD（AD+1） AD4 或5（舍去） DC2AC2AD2 DC2， t
21、anABDtanACD2； 方法二：如图所示：可得ABDACD， E+DCE90，DCA+DCE90， DCAE， 又ADCCDE90， CDEADC， ， DC2ADDE AC2DE， 设 DEx，则 AC2x， 则 AC2AD2ADDE， 即（2x）2AD2ADx， 整理得：AD2+ADx20x20， 解得：AD4x 或5x（负数舍去） ， 则 DC2x， 故 tanABDtanACD2 23 【解答】解： （1）抛物线 yx2+bx+c 的顶点 M 的坐标为（1，4） ， ，解得：， 抛物线解析式为：yx2+2x3， 令 y0，得：x2+2x30，解得：x11，x23， A（3，0） ，
22、B（1，0） ， 令 x0，得 y3， C（0，3） ， 设直线 AC 的解析式为：ykx+b， 将 A（3，0） ，C（0，3）代入， 得：，解得：， 直线 AC 的解析式为：yx3； 故答案为：2，3，yx3 （2）设点 D 的坐标为（m，m2+2m3） ， CODMAN， tanCODtanMAN， ， 解得：m， 3m0， m， 故点 D 的坐标为（，2） ； 设直线 AM 的解析式为 ymx+n， 将点 A（3，0） 、M（1，4）代入， 得：，解得：， 直线 AM 的解析式为：y2x6， 当 xt 时，HE（t3）t+3，HF（2t6）2t+6，HP（t2+2t3） ， HEEFHFHEt+3，FPt24t3， HE+EFFP2（t+3）+t2+4t+3（t+3）20， HE+EFFP， 又 HE+FPEF，EF+FPHE， 当3t1 时，线段 HE，EF，FP 总能组成等腰三角形； 由题意得：，即， 整理得：5t2+26t+330， 解得：t13，t2， 3t1， t
