1、已知集合 Ax|x2+2x30，Bx|yln（x），则 AB（ ） A3，0 B3，1 C3，0） D1，0） 2 （5 分）已知 zC，|z+i|+|zi|2，则 z 对应的点 Z 的轨迹为（ ） A椭圆 B双曲线 C抛物线 D线段 3 （5 分）设 alog0.70.8，blog110.9，c1.10.9，那么（ ） Aabc Bacb Cbac Dcab 4 （5 分） “干支纪年法”是中国历法上自古以来使用的纪年方法，甲、乙、丙、丁、戊、 己、庚、辛、壬、癸被称为“十天干” ，子、丑、寅、卯、辰、巳、午、未、申、酉、戌、 亥叫做“十二地支” “天干”以“甲”字开始， “地支”以“子”字
2、开始，两者按干支顺 序相配，组成了干支纪年法，其相配顺序为：甲子、乙丑、丙寅癸酉，甲戌、乙亥、 丙子癸未，甲申、乙酉、丙戌癸巳，共得到 60 个组合，称六十甲子，周而复始， 无穷无尽 2019 年是 “干支纪年法” 中的己亥年， 那么 2026 年是 “干支纪年法” 中的 （ ） A甲辰年 B乙巳年 C丙午年 D丁未年 5 （5 分）函数的部分图象大致是（ ） A B C D 6 （5 分）在普通高中新课程改革中，某地实施“3+1+2”选课方案该方案中“2”指的是 从政治、地理、化学、生物 4 门学科中任选 2 门，假设每门学科被选中的可能性相等， 那么政治和地理至少有一门被选中的概率是（ ）
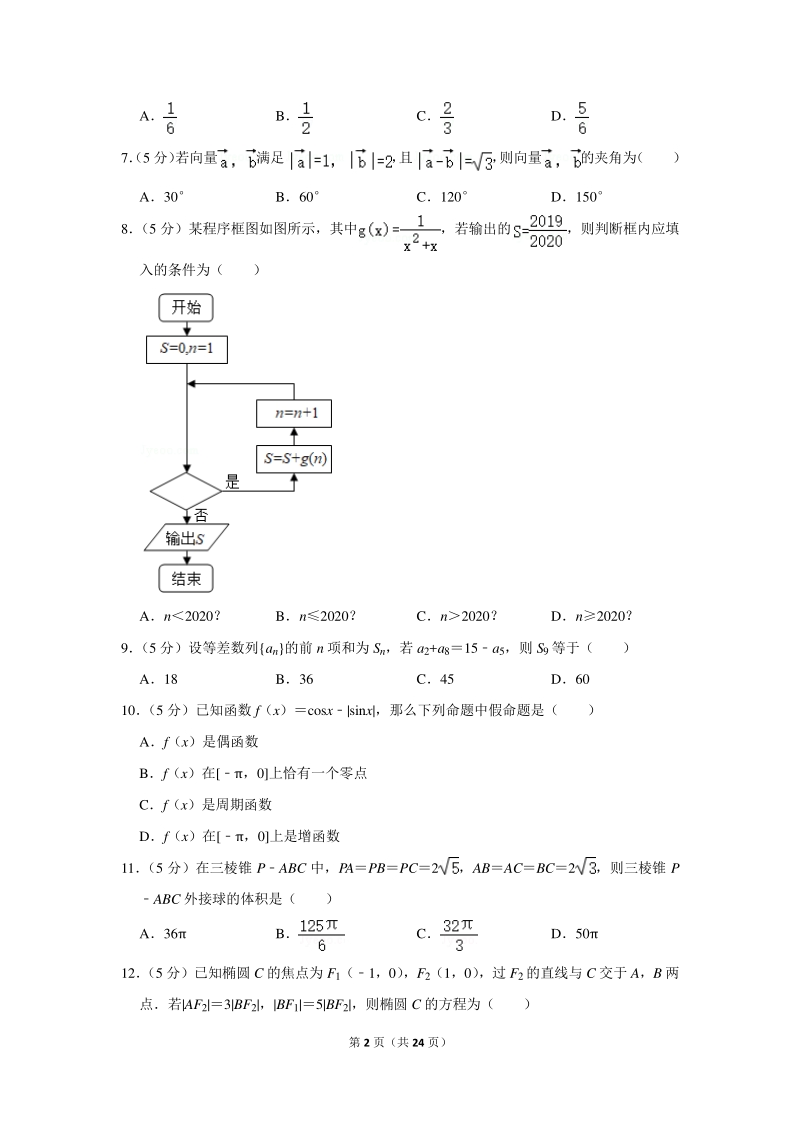
3、 第 2 页（共 24 页） A B C D 7（5 分） 若向量满足， 且， 则向量的夹角为 （ ） A30 B60 C120 D150 8 （5 分）某程序框图如图所示，其中，若输出的，则判断框内应填 入的条件为（ ） An2020？ Bn2020？ Cn2020？ Dn2020？ 9 （5 分）设等差数列an的前 n 项和为 Sn，若 a2+a815a5，则 S9等于（ ） A18 B36 C45 D60 10 （5 分）已知函数 f（x）cosx|sinx|，那么下列命题中假命题是（ ） Af（x）是偶函数 Bf（x）在，0上恰有一个零点 Cf（x）是周期函数 Df（x）在，0上是增函
4、数 11 （5 分）在三棱锥 PABC 中，PAPBPC2，ABACBC2，则三棱锥 P ABC 外接球的体积是（ ） A36 B C D50 12 （5 分）已知椭圆 C 的焦点为 F1（1，0） ，F2（1，0） ，过 F2的直线与 C 交于 A，B 两 点若|AF2|3|BF2|，|BF1|5|BF2|，则椭圆 C 的方程为（ ） 第 3 页（共 24 页） A B C D 二、填空题：本大题共二、填空题：本大题共 4 小题，每小题小题，每小题 5 分，共分，共 20 分分.请将答案填在答题卡的相应位置上请将答案填在答题卡的相应位置上. 13 （5 分）曲线 yx+cosx 在点（0，1
5、）处的切线方程为 14 （5 分）某工厂为了解产品的生产情况，随机抽取了 100 个样本若样本数据 x1，x2， x100的方差为 16，则数据 2x11，2x21，2x1001 的方差为 15 （5 分）设 F 为双曲线 C：的右焦点，O 为坐标原点，以 OF 为直径的圆与圆 x2+y2a2交于 P，Q 两点，若|PQ|OF|，则 C 的离心率为 16 （5 分）在ABC 中，角 A，B，C 的对边分别为 a，b，c，c4，且 C 为锐角，则ABC 面积的最大值为 三、解答题：满分三、解答题：满分 60 分分.解答应写出文字说明、证明过程或演算步骤解答应写出文字说明、证明过程或演算步骤.第第
6、 1721 题为必考题，题为必考题， 每个试题考生都必须作答，第每个试题考生都必须作答，第 22、23 题为选考题，考生根据要求作答题为选考题，考生根据要求作答.（一）必考题：共（一）必考题：共 60 分分. 17 （ 12分 ） 在 等 比 数 列 bn 中 ， 公 比 为q （ 0 q 1 ）， （）求数列bn的通项公式； （）设 cn（3n1）bn，求数列cn的前 n 项和 Tn 18 （12 分）如图，在直三棱柱 ABCA1B1C1中，A1B1A1C1，D 是 B1C1的中点，A1A A1B12 （）求证：AB1平面 A1CD； （）异面直线 AB1和 BC 所成角的余弦值为，求几何体
7、 A1B1DCA 的体积 第 4 页（共 24 页） 19 （12 分）已知某保险公司的某险种的基本保费为 a（单位：元） ，继续购买该险种的投保 人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下： 上年度出险次数 0 1 2 3 4 保费（元） 0.9a a 1.5a 2.5a 4a 随机调查了该险种的 400 名续保人在一年内的出险情况，得到下表： 出险次数 0 1 2 3 4 频数 280 80 24 12 4 该保险公司这种保险的赔付规定如下： 出险序次 第 1 次 第 2 次 第 3 次 第 4 次 第 5 次及以上 赔付金额（元） 2.5a 1.5a a 0.5a 0
8、将所抽样本的频率视为概率 （）求本年度续保人保费的平均值的估计值； （）按保险合同规定，若续保人在本年度内出险 3 次，则可获得赔付（2.5a+1.5a+a） 元；若续保人在本年度内出险 6 次，则可获得赔付（2.5a+1.5a+a+0.5a）元；依此类推， 求本年度续保人所获赔付金额的平均值的估计值； （）续保人原定约了保险公司的销售人员在上午 10：3011：30 之间上门签合同，因 为续保人临时有事，外出的时间在上午 10：4511：05 之间，请问续保人在离开前见到 销售人员的概率是多少？ 20 （12 分）已知点（1，e） ，在椭圆 C：上，其中 e 为 椭圆的离心率，椭圆的右顶点为
9、 D （）求椭圆 C 的方程； 第 5 页（共 24 页） （） 直线 l 过椭圆 C 的左焦点 F 交椭圆 C 于 A， B 两点， 直线 DA， DB 分别与直线 交于 N，M 两点，求证： 21 （12 分）已知函数 f（x）2lnx+x2ax（aR）有两个极值点 x1，x2，其中 x1x2 （）求实数 a 的取值范围； （）当时，求 f（x1）f（x2）的最小值 （二）选考题：共（二）选考题：共 10 分分.请考生从给出的第请考生从给出的第 22、23 题中任选一题作答，并用题中任选一题作答，并用 2B 铅笔在答铅笔在答 题卡上把所选题目对应的题号涂黑，注意所做题目的题号必须与所涂题号
10、一致，如果多做，题卡上把所选题目对应的题号涂黑，注意所做题目的题号必须与所涂题号一致，如果多做， 则按所做的第一题计分则按所做的第一题计分.选修选修 4-4：坐标系与参数方程：坐标系与参数方程 22 （10 分）在直角坐标系 xOy 中，以坐标原点 O 为极点，x 轴正半轴为极轴，建立极坐标 系，曲线 C1：24sin+20，曲线 C2： （）求曲线 C1，C2的直角坐标方程； （）已知曲线 C1与 y 轴交于 A，B 两点，P 为曲线 C2上任一点，求|PA|+|PB|的最小值 选修选修 4-5：不等式选讲：不等式选讲 23已知函数 f（x）|x+t|的单调递增区间为2，+） （）求不等式
11、f（x）+1|2x+1|的解集 M； （）设 a，bM，证明：|a+b|ab+1| 第 6 页（共 24 页） 2019-2020 学年广东省华南师大附中、实验中学、广雅中学、深学年广东省华南师大附中、实验中学、广雅中学、深 圳中学高三（上）期末数学试卷（文科）圳中学高三（上）期末数学试卷（文科） 参考答案与试题解析参考答案与试题解析 一、选择题：本大题共一、选择题：本大题共 12 小题，每小题小题，每小题 5 分，共分，共 60 分分.在每小题给出的四个选项中，只有在每小题给出的四个选项中，只有 一项是符合题目要求的一项是符合题目要求的. 1 （5 分）已知集合 Ax|x2+2x30，Bx|
12、yln（x），则 AB（ ） A3，0 B3，1 C3，0） D1，0） 【分析】分别求出集合 A，B，由此能求出 AB 【解答】解：集合 Ax|x2+2x30x|3x1， Bx|yln（x）x|x0， ABx|3x03，0） 故选：C 【点评】本题考查交集的求法，考查一元二次不等解法、对数函数性质、集合的运算等 基础知识，考查运算求解能力，是基础题 2 （5 分）已知 zC，|z+i|+|zi|2，则 z 对应的点 Z 的轨迹为（ ） A椭圆 B双曲线 C抛物线 D线段 【分析】利用|z+i|+|zi|2，表示复数 Z 对应的点 Z 到点 A（0，1）和到点 B（0，1） 的之和等于 2|A
13、B|，得到 Z 的轨迹是线段 【解答】解：复数 Z 满足条件|z+i|+|zi|2，它表示复数 Z 对应的点 Z 到点 A（0， 1）和到点 B（0，1）的之和等于 2|AB|， 故点 Z 的轨迹是以 A、B 为端点的线段， 故选：D 【点评】本题考查两个复数差的绝对值的几何意义，复数与复平面内对应点之间的关系， 复数的模的定义，判断条件代表的几何意义，是解题的关键 3 （5 分）设 alog0.70.8，blog110.9，c1.10.9，那么（ ） Aabc Bacb Cbac Dcab 【分析】利用指数函数和对数函数的单调性并引入 1 和 0 即可得出结论 【解答】解：log0.710a
14、log0.70.8log0.70.71， 第 7 页（共 24 页） blog110.9log1110， c1.10.91.101； cab 故选：C 【点评】本题主要考查指数函数和对数函数的单调性，以及增函数和减函数的定义，指 数函数的值域，属于基础题 4 （5 分） “干支纪年法”是中国历法上自古以来使用的纪年方法，甲、乙、丙、丁、戊、 己、庚、辛、壬、癸被称为“十天干” ，子、丑、寅、卯、辰、巳、午、未、申、酉、戌、 亥叫做“十二地支” “天干”以“甲”字开始， “地支”以“子”字开始，两者按干支顺 序相配，组成了干支纪年法，其相配顺序为：甲子、乙丑、丙寅癸酉，甲戌、乙亥、 丙子癸未，甲
15、申、乙酉、丙戌癸巳，共得到 60 个组合，称六十甲子，周而复始， 无穷无尽 2019 年是 “干支纪年法” 中的己亥年， 那么 2026 年是 “干支纪年法” 中的 （ ） A甲辰年 B乙巳年 C丙午年 D丁未年 【分析】由简单的合情推理结合阅读，理解“干支纪年法” ，通过运算可得解 【解答】解：因为公元元年是辛酉年，再过 3 年就是甲子年，而 202632023，2023 除以 10 余数是 3，2023 除以 12 余数是 7，所以是丙午年， 故选：C 【点评】本题考查了简单的合情推理及阅读能力，属中档题 5 （5 分）函数的部分图象大致是（ ） A B C D 【分析】利用函数的奇偶性可
16、排除 A，利用特殊点的函数值可排除 CD 【解答】解：函数的定义域为x|x0，故 第 8 页（共 24 页） 函数 f（x）为奇函数，其图象关于原点对称，故排除 A； 当 x 时，故排除 C； 当时，故排除 D； 故选：B 【点评】本题考查函数图象的确定，考查数形结合思想，属于基础题 6 （5 分）在普通高中新课程改革中，某地实施“3+1+2”选课方案该方案中“2”指的是 从政治、地理、化学、生物 4 门学科中任选 2 门，假设每门学科被选中的可能性相等， 那么政治和地理至少有一门被选中的概率是（ ） A B C D 【分析】本题可从反面思考，两门至少有一门被选中的反面是两门都没被选中两门都
17、没被选中包含 1 个基本事件，代入概率公式，即可得到两门都没被选中的概率，则两门 至少有一门被选中的概率可得 【解答】解：设 A两门至少有一门被选中，则 两门都没被选中， 包含 1 个基 本事件，则 p（ ），P（A）1 故选：D 【点评】本题考查了古典概型的概率计算，属于基础题 7（5 分） 若向量满足， 且， 则向量的夹角为 （ ） A30 B60 C120 D150 【分析】由题意利用两个向量的夹角公式，求出向量的夹角 【解答】解：向量满足，且， 2+12+43， 1 设向量的夹角为 ，则 0，2， 由 cos， 第 9 页（共 24 页） 60， 故选：B 【点评】本题主要考查两个向量
18、的夹角公式，属于基础题 8 （5 分）某程序框图如图所示，其中，若输出的，则判断框内应填 入的条件为（ ） An2020？ Bn2020？ Cn2020？ Dn2020？ 【分析】根据已知可得，则 Sg（1）+g（2）+g（3） +g（n），所以 n2019，再由判断框可得 n 条件 【解答】解：由题得，则 Sg（1）+g（2）+g（3）+ g（n）， 因为 S，故 n2019，由于判断框为否时输出，故 n2020， 故选：A 【点评】本题考查程序框图，属于基础题 9 （5 分）设等差数列an的前 n 项和为 Sn，若 a2+a815a5，则 S9等于（ ） A18 B36 C45 D60 【
19、分析】 由等差数列的通项公式知 a2+a815a5a55， 再由等差数列的前 n 项和公式 知 S92a5 第 10 页（共 24 页） 【解答】解：a2+a815a5， a55， S92a545 故选：C 【点评】本题考查等差数列的性质和应用，解题时要注意等差数列的通项公式和前 n 项 和公式的合理运用 10 （5 分）已知函数 f（x）cosx|sinx|，那么下列命题中假命题是（ ） Af（x）是偶函数 Bf（x）在，0上恰有一个零点 Cf（x）是周期函数 Df（x）在，0上是增函数 【分析】A，根据函数奇偶性定义判断 f（x）是定义域 R 上的偶函数； B，x，0时 f（x）sin（x
20、+） ，恰有一个零点是； C，根据正弦、余弦函数的周期性知函数 f（x）是最小正周期为 2 的周期函数； D，x，0时，f（x）sin（x+） ，在，0上先减后增 【解答】解：对于 A，函数 f（x）cosx|sinx|，定义域为 R， 且满足 f（x）cos（x）|sin（x）|cosx|sinx|f（x） ，f（x）为定义域 R 上的 偶函数，A 正确； 对于 B，x，0时，sinx0，f（x）cosx|sinx|cosx+sinxsin（x+） ， 且 x+，f（x）在，0上恰有一个零点是，B 正确； 对于 C，根据正弦、余弦函数的周期性知，函数 f（x）是最小正周期为 2 的周期函数，
21、 C 正确； 对于 D，x，0时，f（x）sin（x+） ，且 x+，f（x）在 ，0上先减后增，D 错误 故选：D 【点评】本题考查了正弦、余弦函数的单调性与奇偶性应用问题，是中档题 11 （5 分）在三棱锥 PABC 中，PAPBPC2，ABACBC2，则三棱锥 P ABC 外接球的体积是（ ） 第 11 页（共 24 页） A36 B C D50 【分析】由题意画出图形，求出三棱锥的高，利用勾股定理求外接球的半径，再由球的 体积公式求解 【解答】解：如图，设 O为ABC 外接圆的圆心，O 为三棱锥 PABC 外接球的球心 ABACBC，2 PAPBPC， 设三棱锥 PABC 外接球的半径
22、为 R，则（4R）2+4R2，解得 R， 故三棱锥 PABC 外接球的体积是 故选：B 【点评】本题考查多面体外接球体积的求法，考查数形结合的解题思想方法，是中档题 12 （5 分）已知椭圆 C 的焦点为 F1（1，0） ，F2（1，0） ，过 F2的直线与 C 交于 A，B 两 点若|AF2|3|BF2|，|BF1|5|BF2|，则椭圆 C 的方程为（ ） A B C D 【分析】根据椭圆的定义以及余弦定理列方程可解得 a，再由隐含条件求得 b，则椭圆的 方程可求 【解答】解：|BF1|5|BF2|，且|BF1|+|BF2|2a，|BF2|，|BF1|， |AF2|3|BF2|，|AF2|a
23、， |AF1|+|AF2|2a，|AF1|a， |AF1|AF2|，则 A 在 y 轴上 第 12 页（共 24 页） 在 RtAF2O 中，cosAF2O， 在BF1F2中，由余弦定理可得 cosBF2F1， 根据 cosAF2O+cosBF2F10，可得， 解得 a22，b2a2c21 椭圆 C 的方程为： 故选：A 【点评】本题考查椭圆方程的求法，考查直线与椭圆位置关系的应用，考查计算能力， 是中档题 二、填空题：本大题共二、填空题：本大题共 4 小题，每小题小题，每小题 5 分，共分，共 20 分分.请将答案填在答题卡的相应位置上请将答案填在答题卡的相应位置上. 13 （5 分）曲线
24、yx+cosx 在点（0，1）处的切线方程为 yx+1 【分析】由题可判断出点在曲线上，所以通过求导求出切线的斜率，把斜率和点代入点 斜式方程即可 【解答】解：点（0，2）在曲线上，斜率 ky（0）1sin01， 所求方程为：yx+1 故答案为：yx+1 【点评】本题考查学生会利用导数求曲线上过某点切线方程的斜率，以及过该点的切线 方程，属于基础题 14 （5 分）某工厂为了解产品的生产情况，随机抽取了 100 个样本若样本数据 x1，x2， x100的方差为 16，则数据 2x11，2x21，2x1001 的方差为 64 【分析】根据样本数据 x1，x2，x100的方差 s2，得出数据 2x
25、11，2x21，2x100 第 13 页（共 24 页） 1 的方差为 22s2，计算即可 【解答】解：样本数据 x1，x2，x100的方差为 s216， 则数据 2x11，2x21，2x1001 的方差为 s222s241664 故答案为：64 【点评】本题考查了方差的定义与计算问题，是基础题 15 （5 分）设 F 为双曲线 C：的右焦点，O 为坐标原点，以 OF 为直径的圆与圆 x2+y2a2交于 P，Q 两点，若|PQ|OF|，则 C 的离心率为 【分析】由题意画出图形，先求出 PQ，再由|PQ|OF|列式求 C 的离心率 【解答】解：如图， 以 OF 为直径的圆的方程为 x2+y2c
26、x0， 又圆 O 的方程为 x2+y2a2， PQ 所在直线方程为 x 把 x代入 x2+y2a2，得 PQ， 再由|PQ|OF|，得c，即 4a2（c2a2）c4， e22，解得 e 故答案为： 【点评】本题考查双曲线的简单性质，考查数形结合的解题思想方法，是中档题 16 （5 分）在ABC 中，角 A，B，C 的对边分别为 a，b，c，c4，且 C 为锐角，则ABC 面积的最大值为 4 【分析】由已知利用正弦定理可求，结合 C 为锐角，可求，利用余弦定 理，基本不等式可求 ab 的最大值，进而根据三角形面积公式即可计算得解 第 14 页（共 24 页） 【解答】解：因为 c4，又， 所以，
27、 又 C 为锐角， 所以 因为， 所以，当且仅当时等号成立， 即， 即当时，ABC 面积的最大值为 故答案为： 【点评】本题主要考查了正弦定理，余弦定理，基本不等式，三角形面积公式在解三角 形中的综合应用，考查了计算能力和转化思想，属于中档题 三、解答题：满分三、解答题：满分 60 分分.解答应写出文字说明、证明过程或演算步骤解答应写出文字说明、证明过程或演算步骤.第第 1721 题题为必考题，为必考题， 每个试题考生都必须作答，第每个试题考生都必须作答，第 22、23 题为选考题，考生根据要求作答题为选考题，考生根据要求作答.（一）必考题：共（一）必考题：共 60 分分. 17 （ 12分
28、） 在 等 比 数 列 bn 中 ， 公 比 为q （ 0 q 1 ）， （）求数列bn的通项公式； （）设 cn（3n1）bn，求数列cn的前 n 项和 Tn 【分析】 （）公比为 q（0q1）的等比数列bn，求得 b1，b3，b5，运用等比数列的 通项公式可得所求； （）求得，运用数列的错位相减法求和，以及等比数列的求和公 式，计算可得所求和 【 解 答 】 解 ：（ ） 因 为 公 比 为q （ 0 q 1 ） 的 等 比 数 列 bn 中 ， ， 所以，当且仅当，时成立 第 15 页（共 24 页） 此时公比， 所以； （）因为， 所以 Tnc1+c2+c3+cn， ， 故数列cn的前
29、 n 项和 【点评】本题考查等比数列的通项公式和求和公式的运用，考查数列的错位相减法求和， 化简运算能力，属于中档题 18 （12 分）如图，在直三棱柱 ABCA1B1C1中，A1B1A1C1，D 是 B1C1的中点，A1A A1B12 （）求证：AB1平面 A1CD； （）异面直线 AB1和 BC 所成角的余弦值为，求几何体 A1B1DCA 的体积 【分析】 （）连结 AC1交 A1C 于点 E，连结 DE，推导出 DEAB1由此能证明 AB1 平面 A1CD （）推导出 AA1A1C1，AC1B1C1，余弦定理得， 由勾股定理可得 A1C13，推导出 C1A1平面 A1B，A1B1平面 A
30、1C，从而 ，由此能求出几何体 A1B1DCA 的体积 第 16 页（共 24 页） 【解答】解： （）证明：如图，连结 AC1交 A1C 于点 E，连结 DE， 因为在直三棱柱 ABCA1B1C1中，四边形 AA1C1C 是矩形， 所以点 E 是 A1C 的中点， 因为 D 是 B1C1的中点，所以 DEAB1 因为 AB1平面 A1CD，DE平面 A1CD， 所以 AB1平面 A1CD （）解：因为棱柱 ABCA1B1C1是直三棱柱， 所以 AA1A1C1， 因为 A1B1A1C1，A1AA1B1，所以 AC1B1C1， 因为异面直线 AB1和 BC 所成角的余弦值为 所以， 因为 A1A
31、A1B12，A1AA1B1，所以 根据余弦定理，在AB1C1中， 可得， 因为 A1B1A1C1，A1B12，所以由勾股定理可得 A1C13， 因为 C1A1A1B1，C1A1A1A，A1AA1B1A1， 所以 C1A1平面 A1B，同理 A1B1平面 A1C， 所以2 所以几何体 A1B1DCA 的体积为 2 【点评】本题考查线面平行的证明，考查几何体的体积的求法，考查空间中线线、线面、 面面间的位置关系等基础知识，考查运算求解能力，是中档题 19 （12 分）已知某保险公司的某险种的基本保费为 a（单位：元） ，继续购买该险种的投保 第 17 页（共 24 页） 人称为续保人，续保人本年度
32、的保费与其上年度出险次数的关联如下： 上年度出险次数 0 1 2 3 4 保费（元） 0.9a a 1.5a 2.5a 4a 随机调查了该险种的 400 名续保人在一年内的出险情况，得到下表： 出险次数 0 1 2 3 4 频数 280 80 24 12 4 该保险公司这种保险的赔付规定如下： 出险序次 第 1 次 第 2 次 第 3 次 第 4 次 第 5 次及以上 赔付金额（元） 2.5a 1.5a a 0.5a 0 将所抽样本的频率视为概率 （）求本年度续保人保费的平均值的估计值； （）按保险合同规定，若续保人在本年度内出险 3 次，则可获得赔付（2.5a+1.5a+a） 元；若续保人在
33、本年度内出险 6 次，则可获得赔付（2.5a+1.5a+a+0.5a）元；依此类推， 求本年度续保人所获赔付金额的平均值的估计值； （）续保人原定约了保险公司的销售人员在上午 10：3011：30 之间上门签合同，因 为续保人临时有事，外出的时间在上午 10：4511：05 之间，请问续保人在离开前见到 销售人员的概率是多少？ 【分析】 （）由题意利用平均值的计算方法可得本年度续保人保费的平均值的估计值； （）由题意可得本年度续保人所获赔付金额的平均值的估计值； （）设保险公司销售人员到达的时间为 x，续保人离开的时间为 y， （x，y）看成平面 上的点，全部结果所构成的区域为 ，可得区域 的
34、面积 S事件 A 表 示 续 保 人 在 离 开 前 见 到 销 售 人 员 ， 可 得 构 成 的 区 域 为 ，即图中的阴影部分，其面 积 S（A） 可得 P（A） 【解答】解： （）由题意可得 保费（元） 0.9a a 1.5a 2.5a 4a 概率 0.7 0.2 0.06 0.03 0.01 第 18 页（共 24 页） 本年度续保人保费的平均值的估计值为 0.9a0.7+a0.2+1.5a0.06+2.5a0.03+4a 0.011.035a； （）由题意可得 赔偿金额（元） 0 2.5a 4a 5a 5.5a 概率 0.7 0.2 0.06 0.03 0.01 本年度续保人所获赔
35、付金额的平均值的估计值 00.7+2.5a0.2+4a0.06+5a 0.03+5.5a0.010.945a； （）设保险公司销售人员到达的时间为 x，续保人离开的时间为 y， （x，y）看成平面 上的点，全部结果所构成的区域为 ， 则区域 的面积 事件 A 表示续保人在离开前见到销售人员， 所构成的区域为， 即图中的阴影部分，其面积 所以，即续保人在离开前见到销售人员的概率是 【点评】本题考查了几何概率计算公式、平均值的计算公式、简易逻辑的判定方法，考 查了推理能力与计算能力，属于中档题 20 （12 分）已知点（1，e） ，在椭圆 C：上，其中 e 为 椭圆的离心率，椭圆的右顶点为 D （
36、）求椭圆 C 的方程； 第 19 页（共 24 页） （） 直线 l 过椭圆 C 的左焦点 F 交椭圆 C 于 A， B 两点， 直线 DA， DB 分别与直线 交于 N，M 两点，求证： 【分析】 （）依题意点（1，e） ，在椭圆 C：上，列 出方程组，求解 a，b 得到椭圆方程 （）由（）得，设 A（x1，y1） ，B（x2，y2） ，N（2，y3） ，M（2，y4） ，把 直线 l：xmy1 代入椭圆方程，得（m2+2）y22my10，利用韦达定理，M、B、D 三点共线，得 N，M 坐标，求解即可 【解答】解： （）依题意点（1，e） ，在椭圆 C：上， 得， 解得 a22，b21， 所
37、以椭圆 C 的方程为 （）由（）得， 如图，设 A（x1，y1） ，B（x2，y2） ，N（2，y3） ，M（2，y4） ， 把直线 l：xmy1 代入椭圆方程，得（m2+2）y22my10， 所以， 因为 M、B、D 三点共线，得， 所以 第 20 页（共 24 页） 同理，由 N、A、D 三点共线，得 因为 所以把代入得 1 所以 【点评】本题考查椭圆方程的求法，直线与椭圆的位置关系的综合应用，考查转化思想 以及计算能力，是难题 21 （12 分）已知函数 f（x）2lnx+x2ax（aR）有两个极值点 x1，x2，其中 x1x2 （）求实数 a 的取值范围； （）当时，求 f（x1）f（
38、x2）的最小值 【分析】 （）依题意得 f（x）的定义域为（0，+） ，根据函数 f（x）有两个极值点 x1，x2，x1x2，可得方程 2x2ax+20 有两个不相等的正根 x1，x2， x1x2，0，0，解得 a 范围 第 21 页（共 24 页） （）因为 x1，x2是方程 2x2ax+20 的两个根，可得，x1x21，由 ，可得，代入 f（x1） f （x2） ， 可得 f （x1） f （x2） 令， 利用导数研究其单调性可得 h（t）在（0，1）上单调递减根据，可得 ，可得，进而得出 t 的取值范围利用单调性可得 h （t）的最小值 【解答】解： （）依题意得 f（x）的定义域为（0
39、，+） ， 因为函数 f（x）有两个极值点 x1，x2，x1x2， 所以方程 2x2ax+20 有两个不相等的正根 x1，x2，x1x2， 所以0，a2160，解得 a4， 此时 f（x）在（0，x1）和（x2，+）上单调递增，在（x1，x2）上单调递减， 所以实数 a 的取值范围是（4，+） （）因为 x1，x2是方程 2x2ax+20 的两个根， 所以，x1x21， 因为， 所以， 所以 令，则 ， 即 h（t）在（0，1）上单调递减 第 22 页（共 24 页） 因为，所以， 所以，即， 所以，即， 所以，0t1， 所以 因为 h（t）在上单调递减， 所以 h（t）的最小值为， 即 f（
40、x1）f（x2）的最小值为 【点评】本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、等 价转化方法，考查了推理能力与计算能力，属于难题 （二）选考题：共（二）选考题：共 10 分分.请考生从给出的第请考生从给出的第 22、23 题中任选一题作答，并用题中任选一题作答，并用 2B 铅笔在答铅笔在答 题卡上把所选题目对应的题号涂黑，注意所做题目的题号必须与所涂题号一致，如果多做，题卡上把所选题目对应的题号涂黑，注意所做题目的题号必须与所涂题号一致，如果多做， 则按所做的第一题计分则按所做的第一题计分.选修选修 4-4：坐标系与参数方程：坐标系与参数方程 22 （10 分）在直角坐
41、标系 xOy 中，以坐标原点 O 为极点，x 轴正半轴为极轴，建立极坐标 系，曲线 C1：24sin+20，曲线 C2： （）求曲线 C1，C2的直角坐标方程； （）已知曲线 C1与 y 轴交于 A，B 两点，P 为曲线 C2上任一点，求|PA|+|PB|的最小值 【分析】 （） 直接利用转换关系， 把参数方程极坐标方程和直角坐标方程之间进行转换 （）利用对称性的应用和不等式的应用求出结果 【解答】解： （）因为曲线 C1：24sin+20，曲线 C2： 所以曲线 C1的直角坐标方程为 x2+y24y+20， 因为， 所以曲线 C2的直角坐标方程为 x+y+10 （）因为曲线 C1与 y 轴交
42、于，两点， 第 23 页（共 24 页） 点 A 关于直线 x+y+10 的对称点为， 所以， 所以|PA|+|PB|的最小值为 【点评】本题考查的知识要点：参数方程极坐标方程和直角坐标方程之间的转换，曲线 的对称性的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型 选修选修 4-5：不等式选讲：不等式选讲 23已知函数 f（x）|x+t|的单调递增区间为2，+） （）求不等式 f（x）+1|2x+1|的解集 M； （）设 a，bM，证明：|a+b|ab+1| 【分析】（1） 先求出 t 的值， 然后根据 f （x） +1|2x+1|， 分 x2，和 三种情况求出 f（x）的解集
43、； （2）要证明|a+b|ab+1|，即证 （ab） 2a2b2+10，然后结合 a，bM，即可证明 （ab） 2a2b2+10 【解答】解： （）f（x）的单调递增区间为2，+） ，t2， 不等式 f（x）+1|2x+1|，可化为|x+2|+1|2x+1|， 当 x2 时，原不等式化为x2+12x1，x0，x2， 当时，原不等式化为 x+2+12x1， 当时，原不等式化为 x+2+12x+1，x2 不等式的解集 Mx|或 x2 （）要证明|a+b|ab+1|， 只需证（ab）2+2ab+1a2+2ab+b2， 即证（ab）2a2b2+10 a，bx|或 x2， （ab）2a2b2+1a2（b21）b2+1（b21） （a21）0， （ab）2a2b2+10，|a+b|ab+1|得证 【点评】本题考查了根据函数的单调性求参数范围，绝对值不等的解法和利用分析法证 明不等式，考查了分类讨论思想，属中档题
