1、 北京市燕山地区北京市燕山地区 2020 年年初中毕业年级质量监测初中毕业年级质量监测 数学试卷数学试卷 2020 年 5 月 考 生 须 知 1本试卷共 8 页，共三道大题，28 道小题。满分 100 分。考试时间 120 分钟。 2在试卷和答题纸上准确填写学校名称、班级、姓名和考号。 3试题答案一律填涂或书写在答题纸上，在试卷上作答无效。 4 在答题纸上， 选择题、 画图题用 2B 铅笔作答， 其他试题用黑色字迹签字笔作答。 5考试结束，请将本试卷和答题纸一并交回。 一、选择题（本题共一、选择题（本题共 16 分分，每每小题小题 2 分）分） 第第 18 题均有四个选项，符合题意的选项题均
2、有四个选项，符合题意的选项只有一个只有一个 1 2020 年 5 月 1 日起， 北京市全面推行生活垃圾分类 下面图标分别为厨余垃圾、 可回收物、 有害垃圾、其他垃圾，其中不是轴对称图形的是 A B C D 2为解决延期开学期间全市初高三学生的学习需求，提升学生的实际获得，北京市教委打造 了“答疑平台”，全市 144000 名初高三学生全部纳入在线答疑辅导范围将 144000 用科 学记数法表示应为 A144 3 10 B14.4 4 10 C1.44 5 10 D1.44 6 10 3方程组 24 21 ， mn mn 的解为 A 3 2 ， m n B 3 2 ， m n C 3 2 ，
3、m n D 3 2 ， m n 4在数轴上，点 A，B 分别表示实数 a，b，将点 A 向左平移 1 个单位长度得到点 C，若点 C， B 关于原点 O 对称，则下列结论正确的是 Aab1 Bab1 Cab1 Dab1 5若一个多边形的内角和是 720 ，则该多边形的边数为 A4 B5 C6 D7 6若 ab1，则代数式 22 2 2 1 b ab ab g的值为 A2 B1 C1 D2 7如图，矩形ABCD 中，BC2AB，点E 在边AD 上，EFBD 于点F若EF1，则 DE 的长为 A3 B5 C2 D3 8为了解高校学生对 5G 移动通信网络的消费意愿，从在校大学生中随机抽取了 100
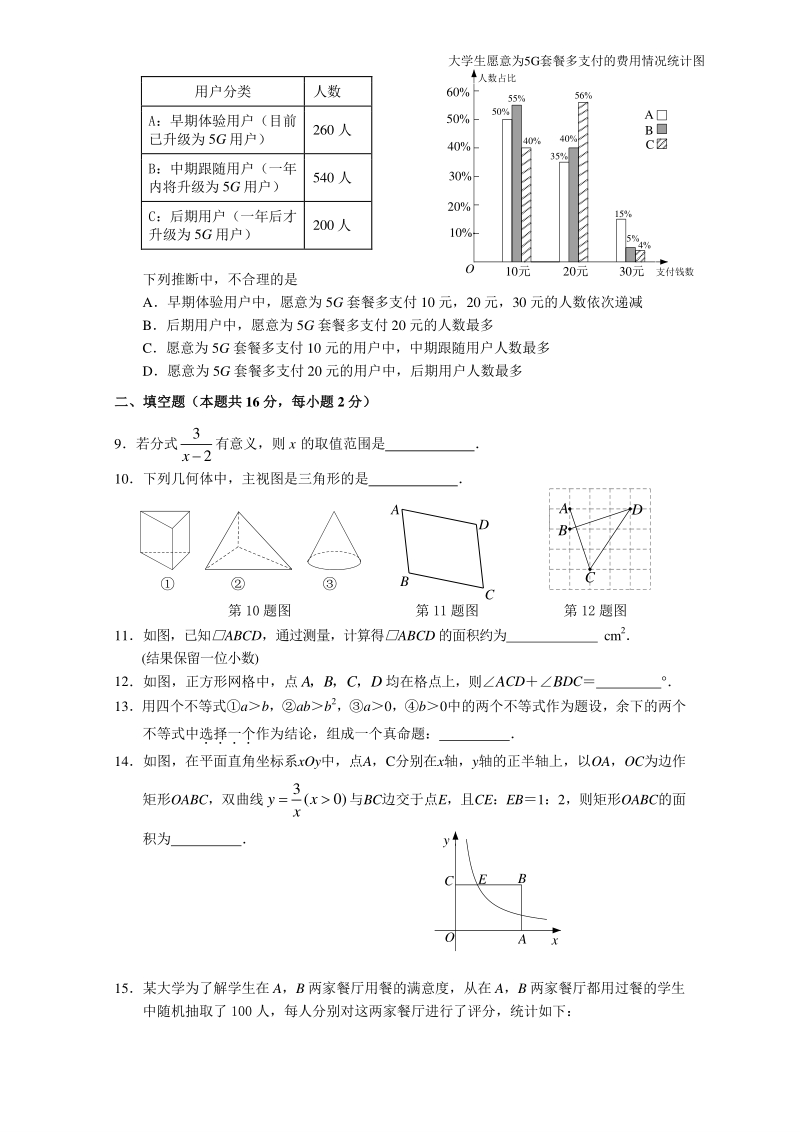
4、0 人进行 调查， 下面是大学生用户分类情况统计表和大学生愿意为 5G 套餐多支付的费用情况统计 图 （例如， 早期体验用户中愿意为5G套餐多支付10元的人数占所有早期体验用户的50%） AE BC F D 用户分类 人数 A：早期体验用户（目前 已升级为 5G 用户） 260 人 B：中期跟随用户（一年 内将升级为 5G 用户） 540 人 C：后期用户（一年后才 升级为 5G 用户） 200人 下列推断中，不合理的是 A早期体验用户中，愿意为 5G 套餐多支付 10 元，20 元，30 元的人数依次递减 B后期用户中，愿意为 5G 套餐多支付 20 元的人数最多 C愿意为 5G 套餐多支付
5、 10 元的用户中，中期跟随用户人数最多 D愿意为 5G 套餐多支付 20 元的用户中，后期用户人数最多 二、填空题（本题共二、填空题（本题共 16 分，每小题分，每小题 2 分）分） 9若分式 3 2x 有意义，则 x 的取值范围是 10下列几何体中，主视图是三角形的是 11如图，已知ABCD，通过测量，计算得ABCD 的面积约为 cm2 (结果保留一位小数) 12如图，正方形网格中，点A，B，C，D均在格点上，则ACDBDC 13用四个不等式ab，abb2，a0，b0中的两个不等式作为题设，余下的两个 不等式中选择一个 作为结论，组成一个真命题： 14如图，在平面直角坐标系xOy中，点A，
6、C分别在x轴，y轴的正半轴上，以OA，OC为边作 矩形OABC，双曲线 3 (0)yx x 与BC边交于点E，且CE：EB1：2，则矩形OABC的面 积为 15某大学为了解学生在 A，B 两家餐厅用餐的满意度，从在 A，B 两家餐厅都用过餐的学生 中随机抽取了 100 人，每人分别对这两家餐厅进行了评分，统计如下： B C A E y x O 大学生愿意为5G套餐多支付的费用情况统计图 C B 15% 5%4% 35% 56% 40% 40% 60% 55% 50% 30元20元 50% 40% 30% 20% A 人数占比 支付钱数 O 10元 10% 第 10 题图 第 12 题图 第 1
7、1 题图 B C A D DA C B DA C B 满意度评分 餐厅 非常满意 （20 分） 较满意 （15 分） 一般 （10 分） 不太满意 （5 分） 非常不满意 （0 分） 合计 A 28 40 10 10 12 100 B 25 20 45 6 4 100 若小芸要在 A，B 两家餐厅中选择一家用餐，根据表格中数据，你建议她去 餐厅(填 A 或 B)，理由是 16已知O如图， (1)作O 的直径 AB； (2)以点 A 为圆心，AO 长为半径画弧，交O 于 C，D 两点； (3)连接 CD 交 AB 于点 E，连接 AC，BC 根据以上作图过程及所作图形，有下面三个推断： CEDE
8、； BE3AE； BC2CE 所有正确推断的序号是 三、解答题三、解答题（本题共（本题共68分，第分，第1722题，每小题题，每小题5分，第分，第2326题，每小题题，每小题6分，第分，第27，28题，题， 每小题每小题7分）分）解答应写出文字说明，演算步骤或证明过程解答应写出文字说明，演算步骤或证明过程 17计算： 1 1 4sin3028 2 18解不等式组： 2 1 2 3 (1)， . xx x 19关于 x 的方程 2 420xxm有两个不相等的实数根，且 m 为正整数，求 m 的值及 此时方程的根 20如图，ABCD 中，点 E，F 分别在边 BC，AD 上，BEDF，AEC90
9、(1) 求证：四边形 AECF 是矩形； (2) 连接 BF，若 AB4，ABC60 ，BF 平分ABC， 求 AD 的长 21抗击新冠肺炎期间，某小区为方便管理，为居民设计了一个身份识别图案系统：在 44 的 正方形网格中，白色正方形表示数字 1，黑色正方形表示数字 0，将第 i 行第 j 列表示的 数记为 ，ij a(其中 i，j 都是不大于 4 的正整数)，例如，图 1 中， 1,2 a0对第 i 行使用公 式 3210 2222 ,1, iiiii Aaaaa进行计算，所得结果 1 A， 2 A， 3 A， 4 A分 别表示居民楼号，单元号，楼层和房间号例如，图 1 中， 3 A 3
10、3 1 2 , a 2 3 2 2 , a 1 3 3 2 , a 0 3 4 2 , a180402119， 4 A080412113， 说明该居民住在 9 层，3 号房间，即 903 号 人 数 F E A BC D 图 2 图 1 E D A C B O (1) 图 1 中， 1 3, a ； (2) 图 1 代表的居民居住在 号楼 单元； (3) 请仿照图 1，在图 2 中画出 8 号楼 4 单元 602 号居民的身份识别图案 22如图，AB 为O 的直径，AC 为弦，点 D 为BC 中点，过点 D 作 DE直线 AC，垂足为 E，交 AB 的延长线于点 F (1) 求证：EF 是O
11、的切线； (2) 若 EF4，sinF 3 5 ，求O 的半径 23 为了解学生居家学习期间对函数知识的掌握情况， 某学校数学教师对九年级全体学生进行 了一次摸底测试， 测试含一次函数、 二次函数和反比例函数三项内容， 每项满分 10 分 现 随机抽取 20 名学生的成绩（成绩均为整数）进行收集、整理、描述和分析，下面给出了 部分信息： a该该20 名名学生一次函数测试成绩如下：学生一次函数测试成绩如下： 7 9 10 9 7 6 8 10 10 8 6 10 10 9 10 9 9 9 10 10 b该该20 名名学生总成绩和二次函数测试成绩情况统计图：学生总成绩和二次函数测试成绩情况统计图
12、： F E D A B C O B 此处恰有两个点完全重合 10986754312 此处恰有三个点完全重合 总成绩 二次函数成绩 A 0 18 19 21 30 24 22 29 28 20 27 26 25 23 c该该20 名名学生总成绩平均分为学生总成绩平均分为25 分分, ,一次函数测试平均分为一次函数测试平均分为8.8 分分 根据以上信息，回答下列问题根据以上信息，回答下列问题: : (1) 该 20 名学生一次函数测试成绩的中位数是 ，众数是 (2) 若该校九年级共有 400 名学生，且总成绩不低于 26 分的学生成绩记为优秀，估计该 校九年级本次测试总成绩优秀的约有 人 (3)
13、在总成绩和二次函数测试成绩情况统计图中，A 同学的一次函数测试成绩是 分；若 B 同学的反比例函数测试成绩是 8 分，则 B 同学的一次函数测试 成绩是 分 (4) 一次函数、 二次函数和反比例函数三项内容中， 学生掌握情况最不好的是 24如图，半圆 O 的直径 AB6cm，点 M 在 线段 AB 上，且 BM1cm，点 P 是AB 上 的动点，过点 A 作 AN直线 PM，垂足 为点 N 小东根据学习函数的经验，对线段 AN，MN，PM 的长度之间的关系进行了 探究 下面是小下面是小东东的探究过程，请补充完整：的探究过程，请补充完整： (1) 对于点 P 在AB 上的不同位置，画图、测量，得
14、到了线段 AN，MN，PM 的长度的几组 值，如下表： 位置 1 位置 2 位置 3 位置 4 位置 5 位置 6 位置 7 AN/cm 0.00 3.53 4.58 5.00 4.58 4.00 0.00 MN/cm 5.00 3.53 2.00 0.00 2.00 3.00 5.00 PM/cm 1.00 1.23 1.57 2.24 3.18 3.74 5.00 在 AN， MN， PM 的长度这三个量中， 确定 的长度是自变量， 和 的长度都是这个自变量的函数； (2) 在同一平面直角坐标系xOy中，画出(1)中所确定的函数的图象； 2 1 3 4 5 6 65431 y/cm O x
15、/cm 2 B M N A O P (3) 结合函数图象，解决问题：当 ANMN 时，PM 的长度约为 cm 25如图，在平面直角坐标系xOy中，直线 l： 3 2 yx与反比例函数(0) k yx x 的图象交 于点 A(2，a) (1) 求 a，k 的值； (2) 横，纵坐标都是整数的点叫做整点点 P(m，n)为射线 OA 上一点，过点 P 作 x 轴，y 轴的垂线，分别交函数(0) k yx x 的图象于点 B，C由线段 PB，PC 和函数 (0) k yx x 的图象在点 B，C 之间的部分所围成的区域(不含边界)记为 W 若 PAOA，求区域 W 内的整点个数； 若区域 W 内恰有
16、5 个整点，结合函数图象，直接写出 m 的取值范围 26在平面直角坐标系xOy中，抛物线 2 3 (0)yaxbxa a经过点 A(1，0) (1) 求抛物线的顶点坐标；(用含 a 的式子表示) (2) 已知点 B(3，4)，将点 B 向左平移 3 个单位长度，得到点 C若抛物线与线段 BC 恰有 一个公共点，结合函数的图象，求 a 的取值范围 27ABC 中，ACB90 ，ACBC 2，M 为 BC 边上的一个动点(不与点 B，C 重合)， 连接 AM，以点 A 为中心，将线段 AM 逆时针旋转 135 ，得到线段 AN，连接 BN (1)依题意补全图 1； l y 1 x 1 O A y
17、x O 1 1 (2)求证：BANAMB； (3)点 P 在线段 BC 的延长线上，点 M 关于点 P 的对称点为 Q，写出一个 PC 的值，使得 对于任意的点 M，总有 AQBN，并证明 28在平面直角坐标系xOy中，过T(半径为 r)外一点 P 引它的一条切线，切点为 Q， 若 0PQ2r，则称点 P 为T 的伴随点 (1) 当O 的半径为 1 时， 在点 A(4，0)，B(0，5)，C(1，3)中，O 的伴随点是 ； 点 D 在直线3yx上，且点 D 是O 的伴随点，求点 D 的横坐标 d 的取值范 围； (2) M 的圆心为 M(m， 0)， 半径为 2， 直线22yx与x轴，y轴分别
18、交于点 E， F 若 线段 EF 上的所有点都是M 的伴随点，直接写出 m 的取值范围 北京市燕山北京市燕山地区地区 2020 年年初中毕业年级质量监测初中毕业年级质量监测 图 1 MCB AA BC 备用图 y x O 1 1 数学试卷数学试卷参考答案与评分标准参考答案与评分标准 2020 年 5 月 一、选择题（本题共一、选择题（本题共 16 分分，每每小题小题 2 分）分） 二、填空题（本题共二、填空题（本题共 16 分，每小题分，每小题 2 分）分） 92x； 10； 113.2； 1290； 13答案不唯一，如，ab，abb2b0； 149； 15答案不唯一，如，选择 A 餐厅，理由
19、是在 A 餐厅用餐非常满意和较满意的人员比例更大 16 三、解答题三、解答题（本题共（本题共68分，第分，第1722题，每小题题，每小题5分，第分，第2326题，每小题题，每小题6分，第分，第27，28题，题， 每小题每小题7分）分） 17解：原式 1 422 22 2 4 分 2222 5 分 18解：原不等式组为 2 1 2 3 (1)， . xx x 解不等式，得 2x， 2 分 解不等式，得5x， 4 分 原不等式组的解集为52 x 5 分 19解：由题意，得 2 44 1 (2)0 m， 1 分 解得2m 2 分 m 为正整数， m=1， 3 分 此时，方程为 2 430xx， 解得
20、 1 3 x， 2 1x 5 分 20(1)证明：ABCD， BCAD，BCAD 又BEDF， BCBEADDF，即 ECAF， EC AF， 四边形 AECF 为平行四边形 1 分 又AEC90 ， 四边形 AECF 是矩形 2 分 (2)解法一： 在 RtABE 中，AEB90 ，ABE60 ，AB4， BE2，AE2 3 3 分 四边形 AECF 是矩形， FCBC，FCAE2 3 BF 平分ABC， 题号 1 2 3 4 5 6 7 8 选项 B C A A C D B D F E A BC D FBC 1 2 ABC30 ， 在 RtBCF 中，FCB90 ，FBC30 ，FC2 3
21、， BC6， ADBC6 5 分 解法二：BF 平分ABC， ABFFBC BCAD， AFBFBC， AFBABF， AFAB4 3 分 在 RtABE 中，AEB90 ，ABE60 ，AB4， BE2， 4 分 FDBE2， ADAFFD6 5 分 21解：(1) 图 1 中， 1,3 a 1 ； 1 分 (2) 图 1 代表的居民居住在 11 号楼 2 单元； 3 分 (3) 8 号楼 4 单元 602 房间居民的身份识别图案如图 5 分 22(1)证法 1：如图，连接 OC，OD， 点 D 为BC 中点， 12 1 2 BOC 1 分 OAOC， A3 1 2 BOC 13， ODAE
22、 EFAE， EFOD 又OD 是O 的半径， EF 是O 的切线 2 分 证法 2：如图，连接 BC，OD， AB 是O 的直径， ACB90 1 分 3 2 1 C B A D E FO 又EFAE， BCEF 点 D 为BC 中点， ODBC， ODEF 又OD 是O 的半径， EF 是O 的切线 2 分 (2) 解：在 RtAEF 中，AEF90，EF4，sinF 3 5 ， AE3，AF5 3 分 ODAE， ODFAEF， ODOF AEAF 4 分 设O 的半径为 r，则 ODr，OFAFAO5r， 5 35 rr 解得 r15 8 ， O 的半径为15 8 5 分 23解：(1
23、) 9，10 2 分 (2) 240 3 分 (3) 10；9 5 分 (4) 二次函数 6 分 24解：(1) PM，AN，MN 2 分 (2) 4 分 (3) 当 ANMN 时，PM 的长度约为 1.23 或 4.06 cm 6 分 25解：(1) 将点 A(2，a)的坐标代入 3 2 yx中，得 3 23 2 a， 将点 A(2，3)的坐标代入 k y x 中，得 k326 2 分 (2) 点 P 为射线 OA 上一点，且 PAOA， A 为 OP 中点， MN AN 2 1 3 4 5 6 65431 y/cm O PM/cm 2 C B A D E FO A(2，3)， 点 P 的坐
24、标为(4，6) 3 分 将4x代入 6 y x 中，得 3 2 y， 将6y代入 6 y x 中，得1x， PB，PC 分别垂直于 x 轴和 y 轴， B(4， 3 2 )，C(1，6)， 结合函数图象可知，区域 W 内有 5 个整点 4 分 2 1 3 m，或104 3 m 6 分 26解：(1)点 A(1，0)在抛物线 2 3 (0)yaxbxa a上， 30 a ba， 即2ba， 1 分 2 23yaxaxa 2 (2 )3a xxa 2 (1)4a xa， 抛物线的顶点坐标为(1，4a) 2 分 (2) 2 23yaxaxa 2 (23)a xx(1)(3)a xx， 抛物线与 x
25、轴交于点 A(1，0)，D(3，0)，与 y 轴交于点 E(0，3a) 由题意得点 C(0，4)，又 B(3，4)， 如图，当0a时，显然抛物线与线段 BC 无公共点 当0a时， 若抛物线的顶点在线段 BC 上，则顶点坐标为(1，4)， 4a4， a1 若抛物线的顶点不在线段 BC 上，由抛物线与线段 BC 恰有一个公共点， 得3a4， 4 3 a， 综上，a 的取值范围是 4 3 a，或 a1 6 分 27(1)补全图形，如图 1 分 y 1 x1 O N C B M A P y 1x 1 O E CB AO 1 x1 y E CB A y 1x 1 O D E CB A (2)证明：ACB
26、90 ，ACBC， ABM45 MABABMAMB180， AMB135MAB 又MAN135， BAN135MAB， BANAMB 3 分 (3) PC 的值为 1 4 分 证明：ACB90 ，ACBC2， AB2 如图，任取满足条件的点 M，作点 M 关于 点 C 的对称点 M，连接 AM， AMAMAN，MM2CM， AMCAMC， AMQAMBBAN 点 M 关于点 P 的对称点为 Q， MQ2MP， MQMQMM2MP2MC2PC2， MQAB， AMQANB， AQBN 7 分 28解：(1)O 的伴随点是 B，C ； 2 分 如图，设点 D 的坐标为(d，d+3)， 当过点 D 的切线长为 2r2 时， OD 22 125， 22 (3)dd5， 解得 1 2 d， 2 1 d 结合图象可知，点 D 的横坐标 d 的取值范围是21 d 5 分 (2) m 的取值范围是1 2 515 m，或34m7 分 说明：各解答题的其他正确解法请参照以上标准按分步给分的原则酌情评分说明：各解答题的其他正确解法请参照以上标准按分步给分的原则酌情评分 M N CB A A CMB N PM Q M25 1 2 M1 D2 D1 y = x + 3 Ox y 1
