1、第 1页（共 6页） 2019 学年第二学期初三数学学年第二学期初三数学调研调研测试试题卷测试试题卷 一选择题（一选择题（每题每题 3 分分） 12020 1 的正确结果是（） A2020B-2020C 2020 1 D 2020 1 - 2 2020 年新型冠状肺炎席卷全球， 截止 2020 年 4 月 30 日， 全球确诊病例约为 322 万人次 数 322 万用科学记数法表示为（） A3.22102B322104C3.22106D3.22105 3下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（） ABCD 4下列因式分解正确的是（） A3ax26ax3（ax22
2、ax）B-x2+y2（x+y） （xy） Ca2+2ab+4b2（a+2b）2Dax2+2axaa（x1）2 5为了了解本次调研测试后我区数学学科各分数段成绩分布情况，从中抽取 400 名考生的 调研测试数学成绩进行统计分析，在这个问题中，样本是指（） A我区 2020 年调研测试数学成绩 B被抽取的 400 名同学 C被抽取的 400 名同学的调研测试数学成绩 D400 6如图，在O 中，弦 AC半径 OB，BOC50，则OBA 的度数为（） A25B50C60D30 7为配合荆州市“我读书，我快乐”读书节活动，某书店推出一种优惠卡，每张卡售价 20 元，凭卡购书可享受 8 折优惠小明同学到
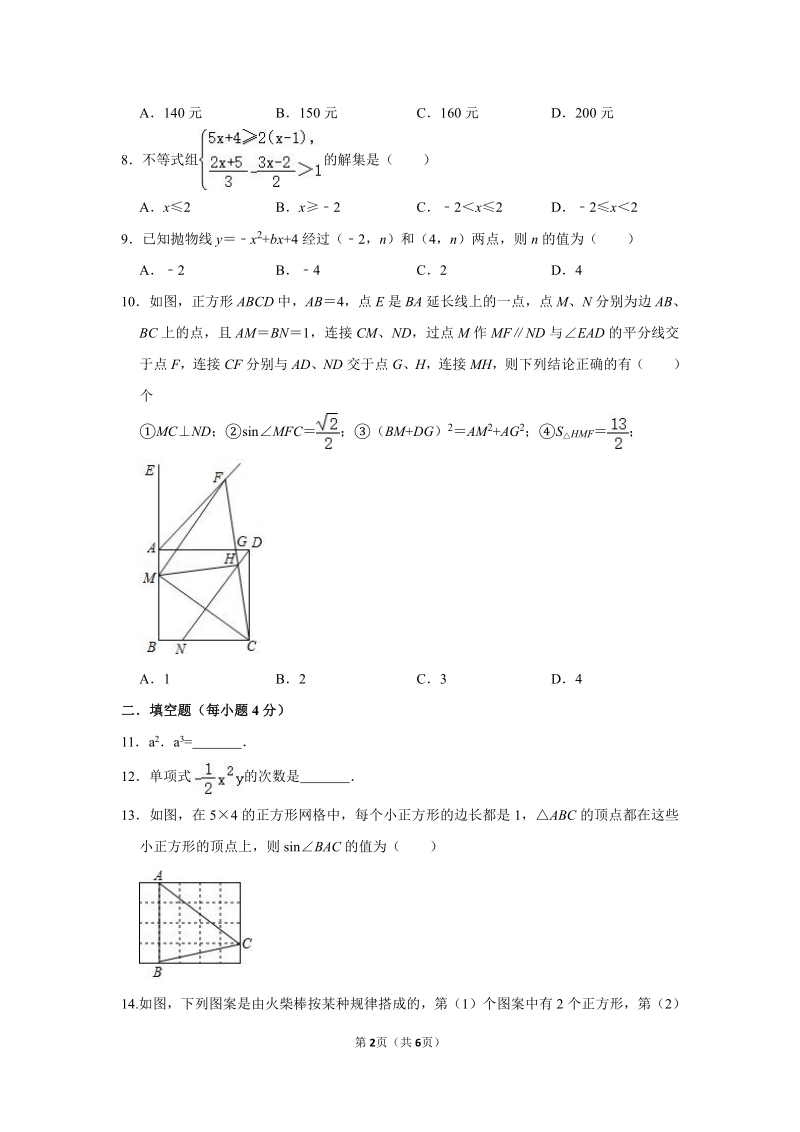
3、该书店购书，她先买优惠卡再凭卡付款，结 果节省了 10 元若此次小明同学不买卡直接购书，则她需付款多少元？（） 第 2页（共 6页） A140 元B150 元C160 元D200 元 8不等式组的解集是（） Ax2Bx2C2x2D2x2 9已知抛物线 yx2+bx+4 经过（2，n）和（4，n）两点，则 n 的值为（） A2B4C2D4 10如图，正方形 ABCD 中，AB4，点 E 是 BA 延长线上的一点，点 M、N 分别为边 AB、 BC 上的点，且 AMBN1，连接 CM、ND，过点 M 作 MFND 与EAD 的平分线交 于点 F，连接 CF 分别与 AD、ND 交于点 G、H，连接
4、 MH，则下列结论正确的有（） 个 MCND；sinMFC；（BM+DG）2AM2+AG2；SHMF； A1B2C3D4 二填空题（二填空题（每小题每小题 4 分分） 11a2a3= 12单项式的次数是 13如图，在 54 的正方形网格中，每个小正方形的边长都是 1，ABC 的顶点都在这些 小正方形的顶点上，则 sinBAC 的值为（） 14.如图，下列图案是由火柴棒按某种规律搭成的，第（1）个图案中有 2 个正方形，第（2） 第 3页（共 6页） 个图案中有 5 个正方形， 第 （3） 个图案中有 8 个正方形， 则第 （5） 个图案中有个 正方形，第 n 个图案中有个正方形 15如图，AO
5、B=30，OD=4，当点 C 在 OA 上运动时，作等腰 RtCDE,CD=DE，则 O,E 两点间距离最小值为 16某城市街角有一草坪，草坪是由一块弓形草地和一块三角形草地组成，为了更科学地管 理草坪，现需要给草坪装上自动喷管装置，并且用喷灌龙头浇水时，既要保证草坪的每 个角落都能浇上水， 又能最大化的节约水， 于是选择了一种转角在 0180内 （含 180） 可以自由设计 （按设定的转角可以往复转动喷灌),再合理设计好喷灌龙头喷水的射程就可 以了 如图，已测出弓形高 DE63m，弓形宽 AB24m，ABC 的边 BC=12m,AC=123m. 若经检测算，将喷灌龙头安装在ABC 的顶点 C
6、 时为最优方案，则： （1）喷灌龙头的最小转角应设置为度. （2）喷灌龙头的最短射程应设置为米 三解答题三解答题 17 （本题 6 分）计算：45cos22-2 2 1 -2020 1 -0 ）（ O A B C E D C 第 4页（共 6页） 18 （本题 6 分）解分式方程 xx 1 2 2 1 2x 19.（本题 6 分）在 44 的方格内选 5 个小正方形，让它们组成一个轴对称图形请在下图 中画出你的 3 种方案.（每 44 的方格内限画一种） 要求： （1）5 个小正方形必须相连（有公共边或公共顶点视为相连） （2）将选中的小正方形方格用黑色签字笔涂成阴影图形（若两个方案的图形经过
7、 翻折，平移，旋转后能够重合，视为一种方案） 示例图 20 （本题 8 分）每年夏季全国各地总有未成年人因溺水而丧失生命，令人痛心疾首今年 某校为确保学生安全，开展了“远离溺水珍爱生命”的防溺水安全知识竞赛现从该校 七、八年级中各随机抽取 10 名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩 得分用 x 表示，共分成四组：A80x85，B85x90，C90x95，D95x 100） ，下面给出了部分信息： 七年级 10 名学生的竞赛成绩是：99，80，99，86，99，96，90，100，89，82 八年级 10 名学生的竞赛成绩在 C 组中的数据是：94，90，94 七、八年级抽取的学
8、生竞赛成绩统计表 年级七年级八年级 平均数9292 中位数93b 众数c100 方差5250.4 根据以上信息，解答下列问题： （1）直接写出上述图表中 a，b，c 的值； （2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好？ 第 5页（共 6页） 请说明理由（一条理由即可） ； （3）该校七、八年级共 720 人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀（x 90）的学生人数是多少？ 21（本题 8 分）如图，在 RtACB 中，ACB=90，以 AC 为直径作O，交 AB 于 点 D. (1)若 AB=8，ABC=30，求O 的半径； （2）若点 E 是边
9、BC 的中点，连 DE，求证：直线 DE 是圆 O 的切线； （3）在（1）的条件下，保持 RtACB 不动，将O 沿直线 BC 向右平移 m 个单位长度 后得到O ，当O与直线 AB 相切时，m= 22 （本题 10 分）2020 年 4 月，我市某药店销售一种疫情防控物品，进价为 50 元/瓶.售价 为 60 元/瓶时，当天的销售量为 100 瓶，在销售过程中发现：售价每上涨 5 元，当天的 销售量就减少 5 瓶，设当天销售单价统一为 x（元/瓶） （x60，且 x 是按 5 元的倍数上 涨） ，当天销售利润为 y 元 （1）求 y 与 x 的函数关系式（不要求写出自变量的取值范围） ；
10、（2）要使当天销售利润不低于 2400 元，求当天销售单价所在的范围； （3）若每瓶物品的利润不超过 80%，要使当天获得利润最大，每瓶物品售价应定为多少 元？当天的最大利润为多少？ 23 （本题 10 分）如果一个三角形有一条边上的高等于这条边的一半，那么我们把这个三角 形叫做“半高三角形” 这条高称为“半高”.如图 1，对于ABC，BC 边上的高 AD 等于 第 6页（共 6页） BC 的一半， ABC 就是半高三角形， 此时， 称ABC 是 “BC 边半高三角形” ， AD 时 “BC 边半高” ；如图 2，对于EFG，EF 边上的高 GH 等于 EF 的一半，EFG 就是半高三角 形，
11、此时，称EFG 是 EF 边半高三角形，GH 是 EF 边半高. （1）在 RtABC 中，ACB=90，AB=10cm，若 ABC 是“BC 边半高三角形” ，则 AC= cm （2）若一个三角形既是等腰三角形又是半高三角形，且“半高”长为 2cm，则该等腰三 角形底边长的所有可能值为 （3）如图 4，平面直角坐标系内，直线 yx+2 与抛物线 yx2交于 R，S 两点，点 P 是 抛物线 yx2上的一个动点， 点 Q 是坐标系内一点， 且使得RSQ 为 “RS 边半高三角形” 当点 P 介于点 R 与点 S 之间，且 PQ 取得最小值时，求点 P 的坐标 24 （本题 12 分）如图，一次
12、函数 yax+b（a0）的图象交 x 轴于点 P，交反比例函数 y （k0）的图象交于 A，B 两点，且 A 点坐标为（1，4） （1）求反比例函数的解析式； （2）若 PA:PB=3：1，求点 P 的坐标. （3）在（2）的条件下，是否存在既相切于直线 AP，又相切于 x 轴，且圆心 C 在反比例 函数图像上的圆？若存在，求出 C 点的横坐标：若不存在，请说明理由. X y o A 第 1页，共 4页 20201919 学年第二学期九年级调研测试学年第二学期九年级调研测试卷卷 数学学科数学学科参考答案与评分标准参考答案与评分标准 一、 选择题选择题（本题共 10 小题，每小题 3 分，共 3
13、0 分） 题号12345678910 答案CCBDCABDBD D 评分标准选对一题给 3 分，不选，多选，错选均不给分 二二、填空题填空题（本题有 6 小题，每小题 4 分，共 24 分） 11. 5 a；12.3 ；13. 5 4 ； 14. 3n115.32216、 （1）90；（2）)11137(（各 2 分，共 4 分） 三、解答题（本题有 8 小题，共 66 分） 17. （本题 6 分） 解：原式12（ 22 ） 21 （ 6 分） （每式化简正确各得 1 分，结论正确得 2 分，共 6 分） 18. （本题 6 分） 解：方程两边同乘(1)x，得22(1)2xx ，解得 2 3
14、 x （ 5 分） 检验：当 2 3 x 时，(1)0x，所以 2 3 x 是原分式方程的解（ 1 分） 所以原分式方程的解为 2 3 x 19 （本题 6 分） 答案不唯一，如下述图形均可： （每答对一个给 2 分，共 6 分） 20.（本题 8 分） 解： （1）a40，b94，c99.（每答对一个给 1 分，共 3 分） （2）结论：八年级学生掌握得较好.（2 分） 理由：但从中位数上看，八年级学生成绩高于七年级学生；从众数上看，八年级得满分的多于七 年级；从方差上看，八年级方差小，成绩相对整齐些，（说出一种即可，1 分） （3）720 13 20 468，故参加此次竞赛活动成绩优秀（x
15、90）的学生人数约 468 人.（2 分） 第 2页，共 4页 21. （本题 8 分） （1）在 RtABC 中，AB=8，ABC=30， AC=ABsinABC=8sin30=4，O 的半径为 2（ 3 分） （2）证明略；（ 3 分） （3）8（ 2 分） 22. （本题 10 分） 解： （1）由题意， 2 60 (50)(1005)2108000 5 x yxxx 故y与x的函数关系式为： 2 2108000yxx （ 3 分） （2）要使当天利润不低于 2400 元，则2400y， 2 21080002400yxx 由解得， 1 80x ， 2 130x 抛物线的开口向下，当天销售
16、单价所在的范围为80130x（ 3 分） （3）每瓶防控物品利润不超过80% ， 50 0.8 x x ，得90x，销售单价为6090x， 由（1）得 2 2108000yxx 对称轴为105x ，60 90x在对称轴的左侧，且y随着x的增大而增大 当 90x 时，取得最大值，此时 2 90 +210 9080002800y 即每瓶物品售价为 90 元时，最大利润为 2800 元 （4 分） 23. （本题 10 分） 解： （1）52；（3 分） （2）4cm 或)262（cm 或)262（cm； （对 1 个 2 分，对 2 个 3 分，对 3 个 4 分） （3）由已知，点 Q 在与 R
17、S 平行的两条直线上，且易得两直线解析式为别为5 xy和1 xy 又点 P 介于点 R 与点 S 之间，且 PQ 取得最小值， 故点 P 即为直线1 xy与抛物线的交点（也是切点） ， 易得 P（ 4 1 2 1， ）（3 分） B A D E O C 第 3页，共 4页 24.（本题 12 分） （1）证明（略）（ 4 分） （2） （3）共有四解，每答对一个给 1 分，共 4 分.具体如下： 过点 D 作 DMAB，垂足为 M，过点 D 作 DNAC，交 AB 于 N. 当点 P 在线段 AM 上时， 4 4 5 DHt， 16 5 PMt， 32 22 5 DFDQt 若DHDF,则 4
18、32 42 55 tt，可得2t （如图-1） ； 若HD HF , 如图，则 0t ； （如图-2） 若，,，故，可得 当点 P 在线段 NM 上时，只有 DH=DF，当点 P 在线段 NB 上时，不存在 16 222) 5 DFDQPMt（ 4 4 5 DHt 416 42() 55 tt故有 26 7 t 解得； B F H D N M A C -3 G A F Q N M CB P H E A P HF D BC 2 2 5 2 E A P H F D B C 2 2 4 9 2 （2 分）分） 5 5 42 AH PFPEPDPA 8197 4+= 42 PFPEPDPC（2 分）分） -1 N M E A P H F D BC Q F E （P、H） D N M A BC 4 4 -2 8 2 5 HDGDDF 4 5 GDDF FHFD 48 32 4(2 ) 555 tt 13 5 t 第 4页，共 4页 综上所述，符合条件的 t 值为：t=0 或 t=2 或 t= 5 13 或 t= 7 26 .（各 1 分，共 4 分）
