1、滕州市级索中学 2020 年 中考数学模拟试题解析 （三） 第卷(选择题共 36 分) 一、选择题：本大题共 12 小题，在每小题给出的四个选项中，只有一项是正确的，请把正 确的选项选出来每小题选对得 3 分，选错、不选或选出的答案超过一个均记零分 1、下列运算正确的是（D） Aa2a3a6Ba3a2aC （a2）3a5Da3a2a 2、如图，直线 1112，130，则2+3（C） A150B180C210D240 第 2 题第 3 题 3、如图，数轴上的点 A，B，O，C，D 分别表示数2，1，0，1，2，则表示数 2的 点 P 应落在（B） A线段 AB 上B线段 BO 上C线段 OC 上
2、D线段 CD 上 4、某学校计划用 34 件同样的奖品全部用于奖励在“经典诵读”活动中表现突出的班级，一 等奖奖励 6 件，二等奖奖励 4 件，则分配一、二等奖个数的方案有（B） A4 种B3 种C2 种D1 种 5、已知 1a3，则化简的结果是（A） A2a5B52aC3D3 6、在平面直角坐标系中，点 P（m3，42m）不可能在（A） A第一象限B第二象限C第三象限D第四象限 7、顺次连接平面上 A、B、C、D 四点得到一个四边形，从ABCDBCADA CBD 四个条件中任取其中两个，可以得出“四边形 ABCD 是平行四边形”这一 结论的情况共有（C） A5 种B4 种C3 种D1 种 8
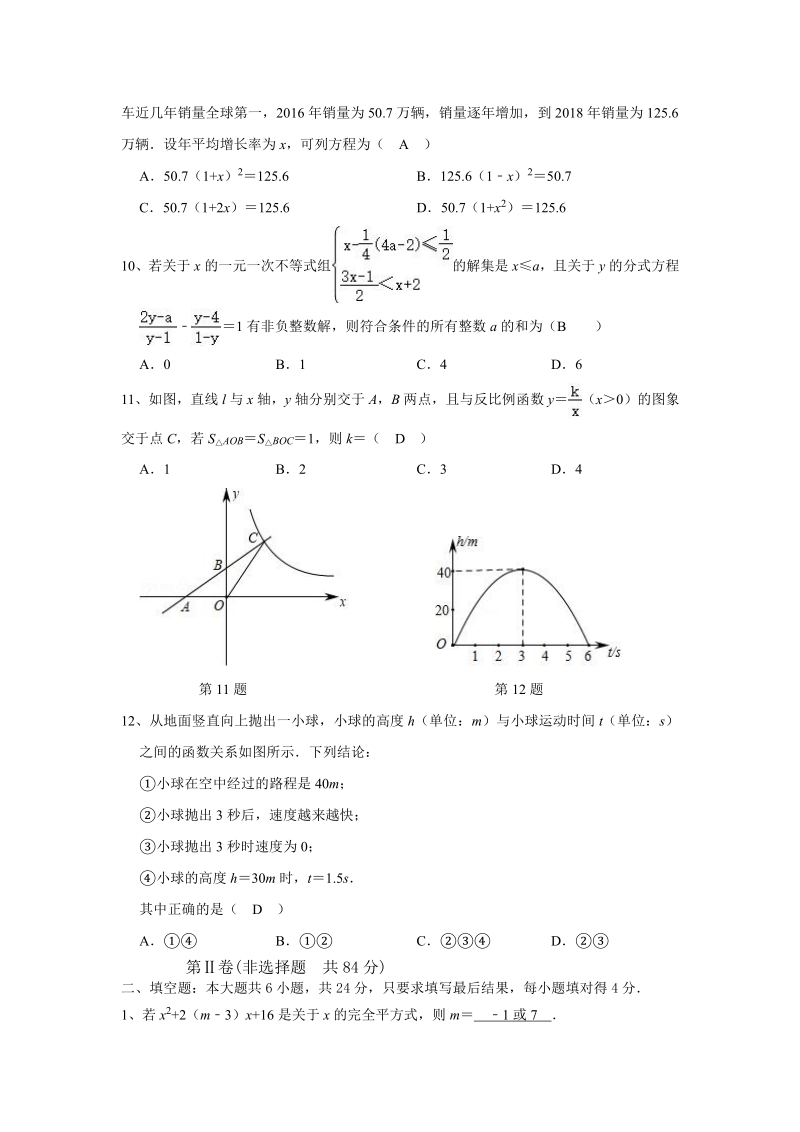
3、、若一组数据 x，3，1，6，3 的中位数和平均数相等，则 x 的值为（A） A2B3C4D5 9、新能源汽车节能、环保，越来越受消费者喜爱，各种品牌相继投放市场，我国新能源汽 车近几年销量全球第一，2016 年销量为 50.7 万辆，销量逐年增加，到 2018 年销量为 125.6 万辆设年平均增长率为 x，可列方程为（A） A50.7（1+x）2125.6B125.6（1x）250.7 C50.7（1+2x）125.6D50.7（1+x2）125.6 10、若关于 x 的一元一次不等式组的解集是 xa，且关于 y 的分式方程 1 有非负整数解，则符合条件的所有整数 a 的和为（B） A0B
4、1C4D6 11、如图，直线 l 与 x 轴，y 轴分别交于 A，B 两点，且与反比例函数 y（x0）的图象 交于点 C，若 SAOBSBOC1，则 k（D） A1B2C3D4 第 11 题第 12 题 12、从地面竖直向上抛出一小球，小球的高度 h（单位：m）与小球运动时间 t（单位：s） 之间的函数关系如图所示下列结论： 小球在空中经过的路程是 40m； 小球抛出 3 秒后，速度越来越快； 小球抛出 3 秒时速度为 0； 小球的高度 h30m 时，t1.5s 其中正确的是（D） ABCD 第卷(非选择题共 84 分) 二、填空题：本大题共 6 小题，共 24 分，只要求填写最后结果，每小题
5、填对得 4 分 1、若 x2+2（m3）x+16 是关于 x 的完全平方式，则 m1 或 7 2、分解因式：b2+c2+2bca2（b+c+a） （b+ca） 3、一个直角三角形斜边上的中线和高线的长分别是 5cm 和 4.8cm，这个三角形的面积为 24。 4、如图，在ABC 中，B30，C45，AD 平分BAC 交 BC 于点 D，DEAB， 垂足为 E若 DE1，则 BC 的长为2+ 第 4 题第 5 题第 6 题 5、如图，PA、PB 分别与O 相切于 A、B 两点，点 C 为O 上一点，连接 AC、BC，若 P50，则ACB 的度数为 65 6、如图，在平面直角坐标系中，四边形 OA
6、BC 为菱形，O（0，0） ，A（4，0） ，AOC60， 则对角线交点 E 的坐标为（3，） 三、解答题：本大题共 7 小题，共 60 分解答要写出必要的文字说明、证明过 程或演算步骤 19、 （本题满分 8 分） 先化简，再求值：（x2） ，其中|x|2 19、解：（x2） ， |x|2，x20，解得，x2， 原式 20、 （本题满分 8 分） 小李要外出参加“建国 70 周年”庆祝活动，需网购一个拉杆箱，图，分别是她上 网时看到的某种型号拉杆箱的实物图与示意图，并获得了如下信息：滑杆 DE，箱长 BC， 拉杆 AB 的长度都相等，B，F 在 AC 上，C 在 DE 上，支杆 DF30cm
7、，CE：CD1：3， DCF45，CDF30，请根据以上信息，解决下列问题 （1）求 AC 的长度（结果保留根号） ； （2）求拉杆端点 A 到水平滑杆 ED 的距离（结果保留根号） 20、解： （1）过 F 作 FHDE 于 H， FHCFHD90， FDC30，DF30， FHDF15，DHDF15， FCH45， CHFH15， ， CE：CD1：3， DECD20+20， ABBCDE， AC（40+40）cm； （2）过 A 作 AGED 交 ED 的延长线于 G， ACG45， AGAC20+20， 答：拉杆端点 A 到水平滑杆 ED 的距离为（20+20）cm 21、 （本题满分
8、 8 分） “墨翟故里，文化滕州” ，我市某中学为传承墨子精神，征集学生书画作品王老师从 全校 20 个班中随机抽取了 A、B、C、D4 个班，对征集作品进行了数量分析统计，绘制了 如下两幅不完整的统计图 （1）王老师采取的调查方式是（填“普查”或“抽样调査” ） ，王老师所调查 的 4 个班共征集到作品件，并补全条形统计图； （2）在扇形统计图中，表示 C 班的扇形圆心角的度数为； （3） 如果全校参展作品中有 4 件获得一等奖， 其中有 1 名作者是男生， 3 名作者是女生 现 要从获得一等奖的作者中随机抽取两人去参加学校的总结表彰座谈会，求恰好抽中一男 一女的概率 （要求用树状图或列表法
9、写出分析过程） 21 解： （1）王老师采取的调查方式是抽样调査，424， 所以王老师所调查的 4 个班共征集到作品 24 件， B 班的作品数为 2441046（件） ， 条形统计图为： （2）在扇形统计图中，表示 C 班的扇形圆心角360150； 故答案为抽样调査；24；150； （3）画树状图为： 共有 12 种等可能的结果数，其中恰好抽中一男一女的结果数为 6， 所以恰好抽中一男一女的概率 22、 （本题满分 8 分） 如图，在四边形 ABCD 中，ABDC，ABAD，对角线 AC，BD 交于点 O，AC 平分 BAD，过点 C 作 CEAB 交 AB 的延长线于点 E，连接 OE （
10、1）求证：四边形 ABCD 是菱形； （2）若 AB，BD2，求 OE 的长 22、解： （1）ABCD， OABDCA， AC 为DAB 的平分线， OABDAC， DCADAC， CDADAB， ABCD， 四边形 ABCD 是平行四边形， ADAB， ABCD 是菱形； （2）四边形 ABCD 是菱形， OAOC，BDAC，CEAB， OEOAOC， BD2， OBBD1， 在 RtAOB 中，AB，OB1， OA2， OEOA2 23、（本题满分 8 分） 如图，在平面直角坐标系中，一次函数 ymx+n（m0）的图象与 y 轴交于点 C，与反 比例函数 y（k0）的图象交于 A，B 两
11、点，点 A 在第一象限，纵坐标为 4，点 B 在第 三象限，BMx 轴，垂足为点 M，BMOM2 （1）求反比例函数和一次函数的解析式 （2）连接 OB，MC，求四边形 MBOC 的面积 23、解： （1）BMOM2， 点 B 的坐标为（2，2） ， 反比例函数 y（k0）的图象经过点 B， 则2，得 k4， 反比例函数的解析式为 y， 点 A 的纵坐标是 4， 4，得 x1， 点 A 的坐标为（1，4） ， 一次函数 ymx+n（m0）的图象过点 A（1，4） 、点 B（2，2） ， ，解得， 即一次函数的解析式为 y2x+2； （2）y2x+2 与 y 轴交于点 C， 点 C 的坐标为（0
12、，2） ， 点 B（2，2） ，点 M（2，0） ， OCMB2， BMx 轴， MBOC， 四边形 MBOC 是平行四边形， 四边形 MBOC 的面积是：OMOC4 24、 （本题满分 8 分） 如图，在 RtABC 中，ACB90，D 是 AC 上一点，过 B，C，D 三点的O 交 AB 于点 E，连接 ED，EC，点 F 是线段 AE 上的一点，连接 FD，其中FDEDCE （1）求证：DF 是O 的切线 （2）若 D 是 AC 的中点，A30，BC4，求 DF 的长 24、解： （1）ACB90，点 B，D 在O 上， BD 是O 的直径，BCEBDE， FDEDCE，BCE+DCEA
13、CB90， BDE+FDE90， 即BDF90， DFBD， 又BD 是O 的直径， DF 是O 的切线 （2）如图，ACB90，A30，BC4， AB2BC248， 4， 点 D 是 AC 的中点， ， BD 是O 的直径， DEB90， DEA180DEB90， ， 在 RtBCD 中，2， 在 RtBED 中，BE5， FDEDCE，DCEDBE， FDEDBE， DEFBED90， FDEDBE， ，即， 25、 （本题满分 12 分） 如图，已知抛物线 yx2+bx+c 的图象经过点 A（1，0） ，B（3，0） ，与 y 轴交于点 C， 抛物线的顶点为 D，对称轴与 x 轴相交于点
14、 E，连接 BD （1）求抛物线的解析式 （2）若点 P 在直线 BD 上，当 PEPC 时，求点 P 的坐标 （3）在（2）的条件下，作 PFx 轴于 F，点 M 为 x 轴上一动点，N 为直线 PF 上一动 点，G 为抛物线上一动点，当以点 F，N，G，M 四点为顶点的四边形为正方形时，求点 M 的坐标 【解答】解： （1）抛物线 yx2+bx+c 的图象经过点 A（1，0） ，B（3，0） ， ， ， 抛物线的解析式为 yx2+2x3； （2）由（1）知，抛物线的解析式为 yx2+2x3； C（0，3） ，抛物线的顶点 D（1，4） ， E（1，0） ， 设直线 BD 的解析式为 ymx
15、+n， ， ， 直线 BD 的解析式为 y2x6， 设点 P（a，2a6） ， C（0，3） ，E（1，0） ， 根据勾股定理得，PE2（a+1）2+（2a6）2，PC2a2+（2a6+3）2， PCPE， （a+1）2+（2a6）2a2+（2a6+3）2， a2， y2（2）62， P（2，2） ， （3）如图，作 PFx 轴于 F， F（2，0） ， 设 M（d，0） ， G（d，d2+2d3） ，N（2，d2+2d3） ， 以点 F，N，G，M 四点为顶点的四边形为正方形，必有 FMMG， |d+2|d2+2d3|， d或 d， 点 M 的坐标为（，0） ， （，0） ， （，0） ， （，0）
