1、数学学科综合能力测试题（全卷共 13 页，这是第 1 页） 2020届初中数学学科综合能力测试题 （暨中考第一次模拟考试）（暨中考第一次模拟考试） 注意： 1.本卷共六大题，23小题，考试时间为120分钟，满分120分. 2.请将答案填写在答题卡上. 一、选择题(本大题共 6 小题，每小题 3 分，共 18 分每小题只有一个正确选项) 15 6 的相反数是( ) A5 6 B5 6 C6 5 D6 5 2.2018 年度感动中国人物揭晓,武汉一位退休老人向家乡木兰县教育局捐赠 1 000 万元,引起了广泛关注. 将 1 000 万用科学记数法表示为 ( ) A.1 10 B.1 107 C.0
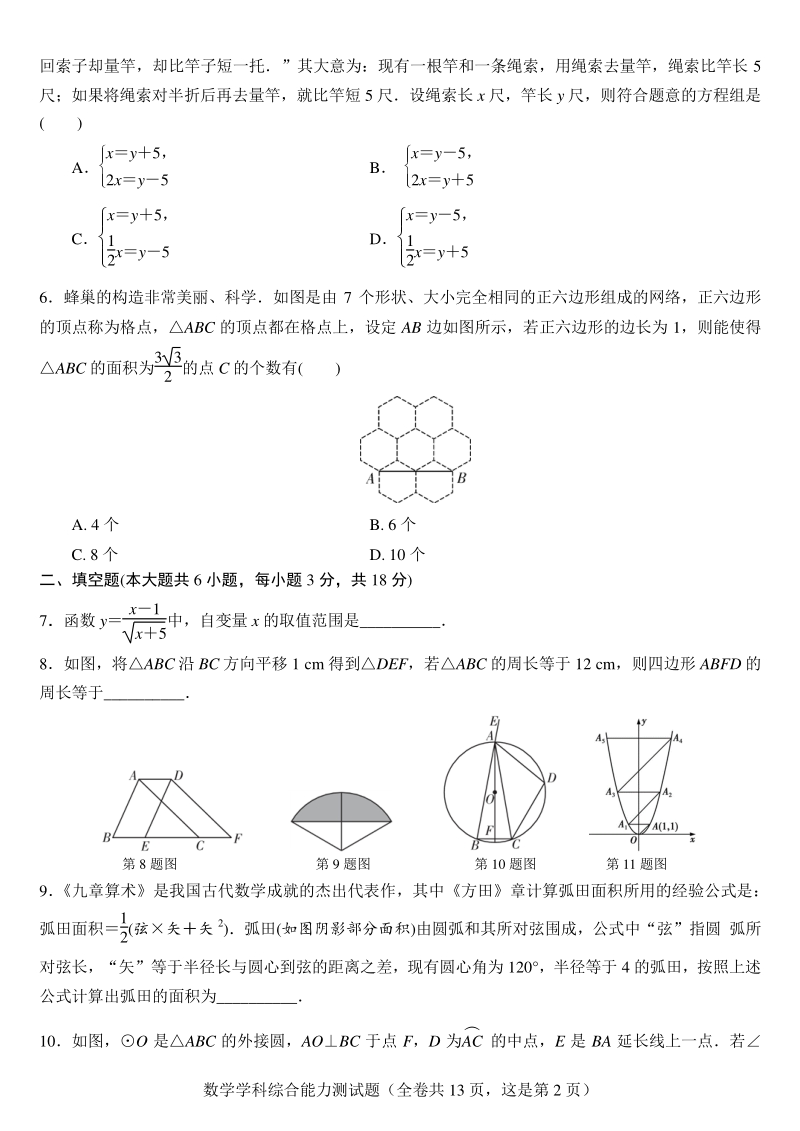
2、.1 109 D.10 106 3.如图所示的立体图形的俯视图是 ( ) A B C D 4.某班班长统计去年 18 月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线 统计图,下列说法正确的是 ( ) A.该班同学每月课外阅读数量的平均数是 50 本 B.众数是 42 本 C.中位数是 58 本 D.每月课外阅读数量超过 40 本的有 4 个月 5 我国古代数学著作 增删算法统宗 记载“绳索量竿”问题： “一条竿子一条索， 索比竿子长一托 折 数学学科综合能力测试题（全卷共 13 页，这是第 2 页） 回索子却量竿，却比竿子短一托”其大意为：现有一根竿和一条绳索，用
3、绳索去量竿，绳索比竿长 5 尺；如果将绳索对半折后再去量竿，就比竿短 5 尺设绳索长 x 尺，竿长 y 尺，则符合题意的方程组是 ( ) A xy5， 2xy5 B xy5， 2xy5 C xy5， 1 2xy5 D xy5， 1 2xy5 6蜂巢的构造非常美丽、科学如图是由 7 个形状、大小完全相同的正六边形组成的网络，正六边形 的顶点称为格点，ABC 的顶点都在格点上，设定 AB 边如图所示，若正六边形的边长为 1，则能使得 ABC 的面积为3 3 2 的点 C 的个数有( ) A. 4 个 B. 6 个 C. 8 个 D. 10 个 二、填空题(本大题共 6 小题，每小题 3 分，共 1
4、8 分) 7函数 y x1 x5中，自变量 x 的取值范围是_ 8如图，将ABC 沿 BC 方向平移 1 cm 得到DEF，若ABC 的周长等于 12 cm，则四边形 ABFD 的 周长等于_ 第 8 题图 第 9 题图 第 10 题图 第 11 题图 9 九章算术是我国古代数学成就的杰出代表作，其中方田章计算弧田面积所用的经验公式是： 弧田面积1 2(弦矢矢 2)弧田(如图阴影部分面积)由圆弧和其所对弦围成，公式中“弦”指圆 弧所 对弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角为 120 ，半径等于 4 的弧田，按照上述 公式计算出弧田的面积为_ 10如图，O 是ABC 的外接圆，
5、AOBC 于点 F，D 为AC 的中点，E 是 BA 延长线上一点若 数学学科综合能力测试题（全卷共 13 页，这是第 3 页） DAE120 ，则CAD_. 11.在平面直角坐标系中,抛物线y=x2如图所示.已知A点坐标为(1,1),过点A作AA1x轴交抛物线于点A1, 过点 A1作A1A2OA 交抛物线于点 A2,过点 A2作A2A3x 轴交抛物线于点A3,过点 A3作 A3A4OA交抛物 线于点 A4依次进行下去,则点 A2 019的坐标为 . 12 在ABC中， AB30 ， BC6， 点P在三角形的边上 若BP2CP， 则CP的长为_ 三、(本大题共 5 小题，每小题 6 分，共 3
6、0 分) 13(1)计算：(a2b)2(a1)(a1)； (2)ABC 是等边三角形，点 E 为射线 AN 上任意一点(点 E 与点 A 不重合)，连接 CE，将线段 CE 绕点 C 顺时针旋转 60 得到线段 CD，直线 DB 交直线 AN 于点 F，交 CE 于点 M.求DFA 的度数 14解不等式组： 3x15x1， x1 2 x2， 并求出它的整数解 15在一个不透明的袋中装有除颜色外其余均相同的 5 个小球，其中黄球 3 个(记为 A1，A2，A3)，绿球 2 个(记为 B1，B2) (1)若先从袋中取出 m(m0)个黄球，再从袋中随机摸出 1 个球，将“摸出绿球”记为事件 A. 填
7、空：若 A 为必然事件，则 m 的值为_； 若 A 为随机事件，则 m 的取值为_； (2)若从袋中随机摸出 2 个球，正好黄球、绿球各 1 个，用画树状图法或列表法求这个事件的概率 16如图，已知ABCDEF，且 A，B，E，D 四点在同一条直线上，请你仅用无刻度的直尺 按要求 作图 (1)如图，作出线段 BE 的垂直平分线； (2)如图，作出线段 AD 的垂直平分线 17如图，矩形 OABC 的顶点 A，C 分别在 x 轴、y 轴的正半轴上，点 B 在反比例函数 yk x(k0)的第一 象限内的图象上，OA3，OC5，动点 P 在 x 轴的上方，且满足 S PAO 3 10S 矩形OABC
8、. (1)若点 P 在这个反比例函数的图象上，求点 P 的坐标； (2)连接 PO，PA，求 POPA 的最小值； 数学学科综合能力测试题（全卷共 13 页，这是第 4 页） (3)若点 Q 是平面内一点，使得以 A，B，P，Q 为顶点的四边形是菱形，则请你直接写出满足条件 的所有点 Q 的坐标 四、(本大题共 3 小题，每小题 8 分，共 24 分) 18入学考试前，某语文老师为了了解所任教的甲、乙两班学生假期期间的语文基础知识背诵情况，对 两个班的学生进行了语文基础知识背诵检测，满分 100 分现从两个班分别随机抽取了 20 名学生的检 测成绩进行整理，描述和分析(成绩得分用 x 表示，共
9、分为五组：A0x80，B80x85，C85x 90，D90x95，E.95x100)，下面给出了部分信息 a甲班 20 名学生的成绩为： 甲 组 82 85 96 73 91 99 87 91 86 91 87 94 89 96 96 91 100 93 94 99 b乙班 20 名学生的成绩在 D 组中的数据是：93,91,92,94,92,92,92. c甲、乙两班抽取的学生成绩数据统计图表： 班级 甲组 乙组 平均数 91 92 中位数 91 b 众数 c 92 方差 41.2 27.3 根据以上信息，解答下列问题： (1)直接写出上述图表中 a，b，c 的值：a_，b_，c_； (2)
10、根据以上数据，你认为甲、乙两个班中哪个班的学生基础知识背诵情况较好？请说明理由；(写 出一条即可) (3)若甲、乙两班总人数为 125，且都参加了此次基础知识检测，估计此次检测成绩优秀(x95)的学 生人数是多少？ 数学学科综合能力测试题（全卷共 13 页，这是第 5 页） 19 图 1 所示是一种淋浴喷头， 图 2 是图 1 的示意图， 若用支架把喷头固定在点 A 处， 手柄长 AB25 cm， AB 与墙壁 DD的夹角DAB37 ，喷出的水流 BC 与 AB 形成的夹角ABC72 .现在住户要求： 当人站在 E 处淋浴时，水流正好喷洒在人体的 C 处，且使 DE50 cm，CE130 cm
11、. (1)安装师傅应将支架固定在离地面多高的位置？ (2)在(1)的条件下，当人从 E 处向墙壁 DD走 10 cm，水流正好喷洒在人体的位置上升了多少？ (结果保留整数 参考数据： sin 37 0.60， cos 37 0.80， tan 37 0.75， sin 72 0.95， cos 72 0.31， tan 72 3.08，sin 35 0.57，cos 35 0.82，tan 35 0.70) 图 1 图 2 20随着南昌市经济的发展，轨道交通连线成网，地铁三号线也预计 2020 年底通车。如图是一个地 铁入口的双翼闸机，示意图如图，它的双翼展开时，双翼边缘的端点 A 与 B 之
12、间的距离为 10 cm，双 翼的边缘 ACBD54 cm，且与闸机侧立面夹角PCAQDB30 . (1)过 A 作 AECP 于 E，求 AE 的长； (2)当双翼收起时，求闸机内侧的宽度是多少？ 数学学科综合能力测试题（全卷共 13 页，这是第 6 页） 五、(本大题共 2 小题，每小题 9 分，共 18 分) 21.数学活动课上，欧阳老师引导同学进行如下探究： 如图 1， 有一个直径为 10 cm 的半圆形铁制模型， 在半圆弧上有一个刚好可以绕弧滑动的小铁环 C， 有一根绷直的橡皮筋穿过小铁环 C，橡皮筋的两头固定在 A，B 点图 2 是示意图 活动一 如图 2，将小铁环 C 沿半圆弧自
13、A 向 B 方向滑动，橡皮筋两段 AC，BC 始终保持绷直状态 数学思考 (1)设 ACx cm，BCy cm，AB 与 BC 的夹角记为 ， 三角形 ABC 是 三角形，夹角 的取值范围是 ； 符合条件下 y 与 x 的函数关系式是 y .自变量 x 的取值范围是 . 活动二 (2)列表：根据(1)中所求函数关系式计算并补全表格 x/cm 10 9 7 6 5 3 2 1 0.5 0 y/cm 0 4.36 7.14 8.66 9.54 9.80 9.95 9.99 描点：根据表中数值，继续描出中剩余的两个点(x，y) 连线：在平面直角坐标系中，请用平滑的曲线画出该函数的图象 数学思考 (3
14、)请你结合函数的图象，写出该函数的两条性质或结论 数学学科综合能力测试题（全卷共 13 页，这是第 7 页） 22.定义：两个相似等腰三角形，如果它们的底角有一个公共的顶点，那么把这两个三角形称为“关联 等腰三角形”如图，在ABC 与AED 中，BABC，EAED，且ABCAED，所以称ABC 与AED 为“关联等腰三角形”，设它们的顶角为 ，连接 EB，DC，则称DC EB为“关联比” 下面是小颖探究“关联比”与 之间的关系的思维过程，请阅读后，解答下列问题： 【特例感知】 (1)当ABC 与AED 为“关联等腰三角形”，且 90 时， 在图中，若点 E 落在 AB 上，则“关联比”DC E
15、B_； 在图中，探究ABE 与ACD 的关系，并求出“关联比”DC EB的值； 【类比探究】 (2)如图， 当ABC 与AED 为“关联等腰三角形”，且 120 时，“关联比”DC EB_； 猜想：当ABC 与AED 为“关联等腰三角形”，且 n 时，“关联比”DC EB_； (直接写出结果，用含 n 的式子表示) 【迁移运用】 (3)如图，ABC 与AED 为“关联等腰三角形”若ABCAED 90 ，AC4，点 P 为 AC 边上一点，且 PA1，点 E 为 PB 上一动点，求点 E 自点 B 运动至点 P 时，点 D 所经过的路径 长 图 数学学科综合能力测试题（全卷共 13 页，这是第
16、8 页） 六、(本大题共 12 分) 23如图，抛物线 y1x2(2a4)xa24a 与 x 轴交于 A，B 两点(点 A 在点 B 的左侧)，过点(2,0)且 平行于 y 轴的直线 l 与抛物线 y1交于点 P. (1)当 a0 时，y1的对称轴为_，AB 长为_； 当 a1 时，y1的对称轴为_，AB 长为_； (2)当 a 为任意值时，AB 的长是否会发生变化，请说明理由； (3)抛物线 y1向右平移 1 个单位长度得到抛物线 y2，抛物线 y2与直线 l 交于点 Q. 线段 PQ 的长为_；(用含 a 的式子表示) 抛物线 y1向右平移 1 个单位长度得到抛物线 y2，y1向右平移 2
17、 个单位长度得到抛物线 y3，y1向右 平移 n1(n 为正整数)个单位长度得到抛物线 yn，当 a3，抛物线 yn与直线 l 交于点 R，四边形 PARB 的面积为 70 时，求 n 的值 参考答案 数学学科综合能力测试题（全卷共 13 页，这是第 9 页） 一、选择题(本大题共 6 小题，每小题 3 分，共 18 分每小题只有一个正确选项) 1 2 3 4 5 6 A B B C C B 二、填空题(本大题共 6 小题，每小题 3 分，共 18 分) 7. x5 8. 14 cm 9. 4 32 10. 40 11. (1 010,1 0102) 12. 2 或 2 3或 1 13（一个一
18、分） 三、(本大题共 5 小题，每小题 6 分，共 30 分) 13(1)原式a24ab4b2a214ab4b21. (2)在等边三角形 ABC 中，ACABCB，ACB60 . 由旋转知DCE60 ACB，CDCE. DCBACE. 在CDB 和CEA 中， CDCE， DCBACE， CBAC， CDBCEA(SAS) CDBCEA. EMFCMD，DFEDCE60 . DFA180 60 120 . 14 3x15x1， x1 2 x2. 解不等式，得 x2. 解不等式，得 x3. 不等式组的解集是2x3. 不等式组的整数解是1,0,1,2,3. 15(1)3；1 或 2. (2)画树状
19、图如图所示 由树状图可知共有 20 种等可能的结果，其中从袋中随机摸出 2 个球，正好黄球、绿球各 1 个的结 数学学科综合能力测试题（全卷共 13 页，这是第 10 页） 果有 12 种， 从袋中随机摸出 2 个球，正好黄球、绿球各 1 个的概率为 12 20 3 5. 16(1)如解图，直线 l 即为求； (2)如解图，直线 l 即为所求 图 图 17(1)OA3，OC5，点 B 的坐标为(3,5) 点 B 在反比例函数 yk x(k0)的图象上，k3 515. 反比例函数的解析式为 y15 x . S PAO 3 10S 矩形OABC，1 2OA yp 3 10OA OC， 即1 2 3
20、yp 3 10 3 5.yp3. 当 y3 时，15 x 3，解得 x5. 当点 P 在这个反比例函数的图象上时，点 P 的坐标为(5,3) (2)由(1)，得点 P 在直线 y3 上，如图，作点 O 关于直线 y3 的对称点 O，连接 AO交直线 y3 于点 P，此时 POPA 取得最小值，且 POPAPOPAAO. 点 O 的坐标为(0,0)， 点 O的坐标为(0,6)，即 OO6. OA3，AO OO2OA23 5. POPA 的最小值为 3 5. (3)点 Q 的坐标为(1,8)或(7,8)或(3 21，2)或(3 21，2) 四、(本大题共 3 小题，每小题 8 分，共 24 分)
21、18(1)40；92.5；91. 数学学科综合能力测试题（全卷共 13 页，这是第 11 页） (2)乙班的学生基础知识背诵情况较好理由：乙班的平均分、中位数都高于甲班(答案不唯一) (3)12562040% 40 44(名) 答：估计此次检测成绩优秀(x95)的学生人数是 44 人 19(1)如图，过点 B 作 BGDD 于点 G，延长 EC，GB 交于点 F. 易得四边形 GDEF 是矩形FGDE，FEGD. 在 RtAGB 中，AB25 cm，GAB 37 ， sin 37 GB AB，cos 37 GA AB. GB250.6015(cm)，GA250.8020(cm) BFGFGBD
22、EGB501535(cm) ABC72 ，GBA90 DAB53 ， CBF55 .BCF90 55 35 . 在 RtBFC 中，tanBCFBF CF，CF 35 0.7050(cm) GDFECFCE50130180(cm) ADGDGA18020160(cm) 安装师傅应将支架固定在离地面约 160 cm 的位置 (2)如图， 在 DE 上取点 E， 使 EE10 cm， 过点 E作 EFBF 于点 F， 交 BC 于点 C， 易得四边形 FEEF是矩形 EFFE，EFFE，FFEE10 cm. 由(1)，得 BF35 cm，CF50 cm，FE180 cm， EFFE180 cm，B
23、FBFFF25(cm) EFFE，BCFBCF. CF CF BF BF ，即 CF 50 25 35.解得 CF 250 7 36(cm) CEEFCF18036144(cm) CECE14413014(cm) 水流正好喷洒在人体的位置上升了 14 cm. 20(1)如图，作 AEPC， 在 RtACE 中，AEAC sinACE541 227(cm) 数学学科综合能力测试题（全卷共 13 页，这是第 12 页） 答：AE 的长为 27 cm； (2)如图，过 B 作 BFDQ 于 F，由(1)得，AE27 cm， 同理 BF27 cm， 又点 A 与 B 之间的距离为 10 cm， 通过闸
24、机的物体的最大宽度为 27102764(cm)， 答：当双翼收起时，闸机内部的宽度是 64 cm. 五、(本大题共 2 小题，每小题 9 分，共 18 分) 21.(1)由圆周角定理的推论可知ABC 是直角三角形，0 90 ； 在 RtABC 中，由勾股定理得 AC2BC2AB2，即 x2y2102， y 102x2，0x10. (2)当 x6 时，y8；当 x0，y10. 点(6,8)，点(0,10)如图所示 函数图象如答图所示 (3)性质 1：函数值 y 的取值范围为 0y10. 性质 2：函数图象在第一象限，y 随 x 的增大而减小(其他符合的答案，参照得分) 22. (1) 2； 当
25、90 时，ABC，AED 均为等腰直角三角形， BACEAD45 ，AC 2AB，AD 2AE. AC AB AD AE 2.又CADEADCAECABCAEBAE， CADBAE.CD BE CA BA 2.“关联比” DC EB为 2； (2) 3； 数学学科综合能力测试题（全卷共 13 页，这是第 13 页） 2cos(90 n 2 )； (3)如图，过点 B 作 BFAC 于点 F. ABC 与AED 为“关联等腰三角形”，ABCAED90 ，AC4， ABC 与AED 均为等腰直角三角形，CFFAFB2. PA1，PF211.在 RtPBF 中，由勾股定理得，PB BF2PF2 22
26、12 5. 连接 CD，由(1)可知ACDABE. ACDABE定角， 点 D 所经过的路径是线段 CD.90 时，“关联比”为 2， 当点 E 自点 B 运动至点 P 时，点 D 所经过的路径长为 5 2 10. 六、(本大题共 12 分) 23解：(1)直线 x2；4；直线 x3；4. (2)当 a 为任意值时，AB 的长不会发生变化理由如下： 当 y0 时，有 x2(2a4)xa24a0， 即(xa)x(a4)0. 解得 x1a，x2a4. 点 A 的坐标为(a,0)，点 B 的坐标为(a4,0) ABa4a4. (3)2a9； 当 a3 时，y1(x1)24， 点 P 的坐标为(2，3) y1向右平移 n1(n 为正整数)个单位长度得到抛物线 yn， ynx1(n1)24(x2n)24. 当 x2 时，ynn24，点 R 的坐标为(2，n24) S四边形PARBSPABSRAB1 234 1 24(n 24)70， n 6. n 为正整数，n6.
