1、（精品资料）（精品资料）20202020 年中考数学压轴题突破年中考数学压轴题突破专题九专题九 动态动态 几何定值问题几何定值问题 类型一 【线段及线段的和差为定值】 【典例指引1】 已知： ABC是等腰直角三角形， BAC90 ， 将 ABC绕点C顺时针方向旋转得到 ABC， 记旋转角为 ，当 90 180 时，作 ADAC，垂足为 D，AD 与 BC 交于点 E （1）如图 1，当CAD15 时，作AEC 的平分线 EF 交 BC 于点 F 写出旋转角 的度数； 求证：EA+ECEF； （2）如图 2，在（1）的条件下，设 P 是直线 AD 上的一个动点，连接 PA，PF，若 AB 2，求
2、线段 PA+PF 的最小值 （结果保留根号） 【举一反三】 如图（1） ，已知 =90MON ,点P为射线ON上一点，且 =4OP，B、C为射线OM和ON上的两个动点 （OCOP） ，过点P作PABC，垂足为点A，且=2PA，联结BP （1）若 1 2 PAC ABOP S S 四边形 时，求tan BPO的值； （2）设PCx， AB y BC 求y与x之间的函数解析式，并写出定义域； （3）如图(2)，过点A作BP的垂线，垂足为点H，交射线ON于点Q，点B、C在射线OM和ON上运动 时， 探索线段OQ的长是否发生变化？若不发生变化， 求出它的值。 若发生变化， 试用含 x 的代数式表示OQ
3、 的长 类型二 【线段的积或商为定值】 【典例指引 2】 如图， 矩形ABCD中，2,5,1ABBCBP， 0 90MPN， 将M P N绕点P从PB 处开始按顺时针方向旋转，PM交边AB（或AD）于点E，PN交边AD（或CD）于点F.当PN旋转 至PC处时，MPN的旋转随即停止. （1）特殊情形：如图，发现当PM过点A时，PN也恰好过点D，此时ABP是否与PCD相似？并 说明理由； （2）类比探究：如图，在旋转过程中， PE PF 的值是否为定值？若是，请求出该定值；若不是，请说明理 由； （3）拓展延伸：设AEt时，EPF的面积为S，试用含t的代数式表示S； 在旋转过程中，若1t 时，求对
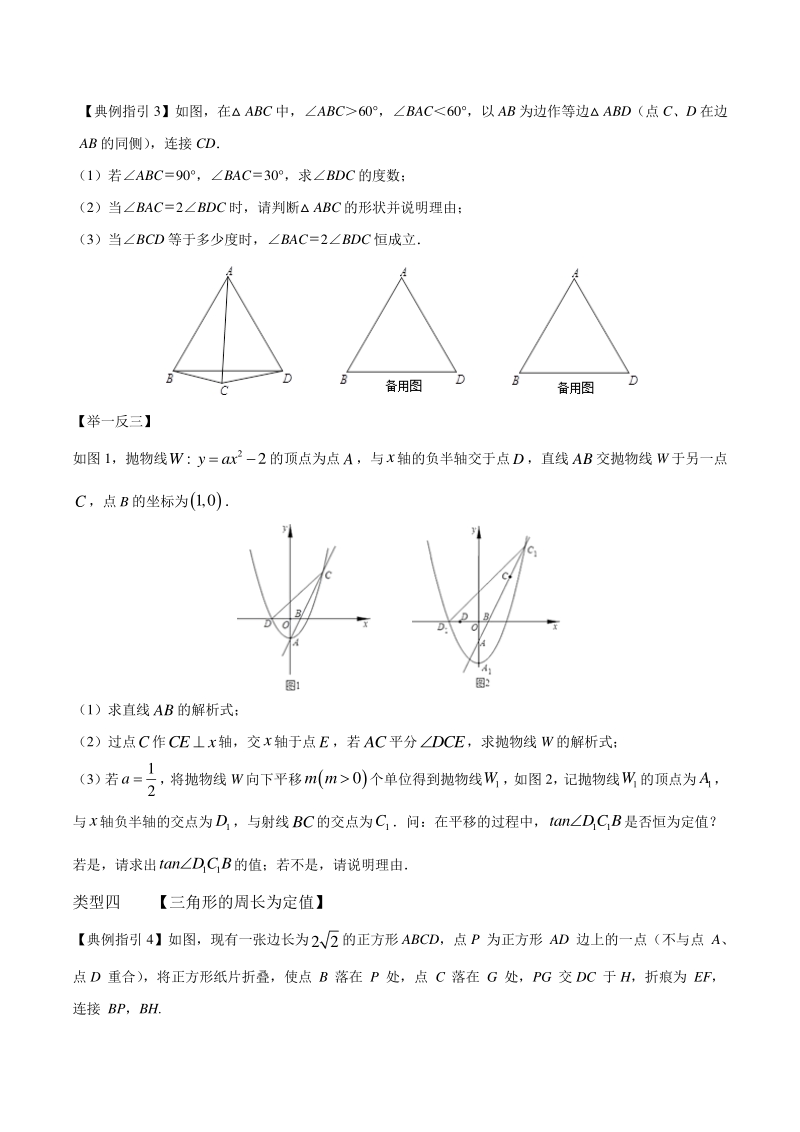
4、应的EPF的面积； 在旋转过程中，当EPF的面积为 4.2 时，求对应的t的值. 【举一反三】 如图 1,已知直线 ya 与抛物线 2 1 4 yx交于 A、B 两点(A 在 B 的左侧),交 y 轴于点 C (1)若 AB4,求 a 的值 (2)若抛物线上存在点 D(不与 A、B 重合),使 1 2 CDAB,求 a 的取值范围 (3)如图2,直线ykx2与抛物线交于点E、 F,点P是抛物线上的动点,延长PE、 PF分别交直线y2于M、 N 两点,MN 交 y 轴于 Q 点,求 QM QN 的值。 图 1 图 2 类型三 【角及角的和差定值】 【典例指引 3】如图，在 ABC 中，ABC60
5、 ，BAC60 ，以 AB 为边作等边 ABD（点 C、D 在边 AB 的同侧） ，连接 CD （1）若ABC90 ，BAC30 ，求BDC 的度数； （2）当BAC2BDC 时，请判断 ABC 的形状并说明理由； （3）当BCD 等于多少度时，BAC2BDC 恒成立 【举一反三】 如图 1，抛物线 2 : 2Wyax的顶点为点A，与x轴的负半轴交于点D，直线AB交抛物线 W 于另一点 C，点B的坐标为1,0 （1）求直线AB的解析式； （2）过点C作CEx轴，交x轴于点E，若AC平分DCE，求抛物线 W 的解析式； （3） 若 1 2 a ， 将抛物线 W 向下平移0m m个单位得到抛物线
6、1 W， 如图 2， 记抛物线 1 W的顶点为 1 A， 与x轴负半轴的交点为 1 D，与射线BC的交点为 1 C问：在平移的过程中， 11 tan DC B是否恒为定值？ 若是，请求出 11 tan DC B的值；若不是，请说明理由 类型四 【三角形的周长为定值】 【典例指引 4】如图，现有一张边长为2 2的正方形 ABCD，点 P 为正方形 AD 边上的一点（不与点 A、 点 D 重合） ，将正方形纸片折叠，使点 B 落在 P 处，点 C 落在 G 处，PG 交 DC 于 H，折痕为 EF， 连接 BP，BH. （1）求证：EPBEBP ； （2）求证：APBBPH ； （3）当点 P 在
7、边 AD 上移动时， PDH 的周长是否发生变化？不变化，求出周长，若变化，说明理由； （4）设 AP 为 x，四边形 EFGP 的面积为 S，求出 S 与 x 的函数关系式. 【举一反三】如图，在等腰直角三角形 ABC 中，C90 ，AB8 2，点 O 是 AB 的中点.将一个边长足 够大的 Rt DEF 的直角顶点 E 放在点 O 处，并将其绕点 O 旋转，始终保持 DE 与 AC 边交于点 G，EF 与 BC 边交于点 H. (1)当点 G 在 AC 边什么位置时，四边形 CGOH 是正方形. (2)等腰直角三角 ABC 的边被 Rt DEF 覆盖部分的两条线段 CG 与 CH 的长度之
8、和是否会发生变化， 如不发 生变化，请求出 CG 与 CH 之和的值：如发生变化，请说明理由. 类型五 【三角形的面积及和差为定值】 【典例指引 5】综合与实践：矩形的旋转 问题情境： 在综合与实践课上，老师让同学们以“矩形的旋转”为主题开展数学活动具体要求：如图 1，将长与宽都相 等的两个矩形纸片 ABCD 和 EFGH 叠放在一起，这时对角线 AC 和 EG 互相重合固定矩形 ABCD，将矩形 EFGH 绕 AC 的中点 O 逆时针方向旋转，直到点 E 与点 B 重合时停止，在此过程中开展探究活动 操作发现： （1）雄鹰小组初步发现：在旋转过程中，当边 AB 与 EF 交于点 M，边 CD
9、 与 GH 交于点 N，如图 2、图 3 所示，则线段 AM 与 CN 始终存在的数量关系是 （2）雄鹰小组继续探究发现：在旋转开始后，当两个矩形纸片重叠部分为四边形 QMRN 时，如图 3 所示， 四边形 QMRN 为菱形，请你证明这个结论 （3）雄鹰小组还发现在问题（2）中的四边形 QMRN 中MQN 与旋转角AOE 存在着特定的数量关系， 请你写出这一关系，并说明理由 实践探究： （4） 在图 3 中， 随着矩形纸片 EFGH 的旋转， 四边形 QMRN 的面积会发生变化 若矩形纸片的长为2+ 2， 宽为 2，请你帮助雄鹰小组探究当旋转角AOE 为多少度时，四边形 QMRN 的面积最大？
10、最大面积是多 少？（直接写出答案） 【举一反三】 如图 1，矩形 ABCD 中，E 是 AD 的中点，以点 E 直角顶点的直角三角形 EFG 的两边 EF，EG 分别过点 B， C，F30 . （1）求证：BECE （2） 将 EFG 绕点 E 按顺时针方向旋转， 当旋转到 EF 与 AD 重合时停止转动.若 EF， EG 分别与 AB， BC 相交于点 M，N.（如图 2） 求证： BEMCEN； 若 AB2，求 BMN 面积的最大值； 当旋转停止时，点 B 恰好在 FG 上（如图 3） ，求 sinEBG 的值. 【新题训练】 1已知在平行四边形 ABCD 中，AB=6，BC=10，BAD
11、=120 ，E 为线段 BC 上的一个动点（不与 B，C 重 合） ，过 E 作直线 AB 的垂线，垂足为 F，FE 与 DC 的延长线相交于点 G， （1）如图 1，当 AEBC 时，求线段 BE、CG 的长度 （2）如图 2，点 E 在线段 BC 上运动时，连接 DE，DF， BEF 与 CEG 的周长之和是否是一个定值，若 是请求出定值，若不是请说明理由 （3）如图 2，设 BE=x， DEF 的面积为 y，试求出 y 关于 x 的函数关系式 2如图，边长为 8 的正方形 OABC 的两边在坐标轴上，以点 C 为顶点的抛物线经过点 A，点 P 是抛物线上 点 A、C 间的一个动点（含端点
12、） ，过点 P 作 PFBC 于点 F，点 D、E 的坐标分别为（0，6） ， （4，0） ， 连接 PD，PE，DE （1）求抛物线的解析式； （2）小明探究点 P 的位置是发现：当点 P 与点 A 或点 C 重合时，PD 与 PF 的差为定值，进而猜想：对于 任意一点 P，PD 与 PF 的差为定值，请你判定该猜想是否正确，并说明理由； （3）请直接写出 PDE 周长的最大值和最小值 3如图，四边形 ABCD 中，ADBC，ABC=90 (1)直接填空：BAD=_ . (2)点 P 在 CD 上，连结 AP，AM 平分DAP，AN 平分PAB，AM、AN 分别与射线 BP 交于点 M、N设
13、 DAM= 求BAN 的度数(用含 的代数式表示) 若 ANBM，试探究AMB 的度数是否为定值？若为定值，请求出该定值；若不为定值，请用 的代数 式表示它 4将在同一平面内如图放置的两块三角板绕公共顶点 A 旋转，连接 BC，DE探究 S ABC与 S ADC的比是 否为定值 （1）两块三角板是完全相同的等腰直角三角板时，S ABC：S ADE是否为定值？如果是，求出此定值，如果 不是，说明理由 （图） （2）一块是等腰直角三角板，另一块是含有 30 角的直角三角板时，S ABC：S ADE是否为定值？如果是， 求出此定值，如果不是，说明理由 （图） （3）两块三角板中，BAE+CAD180
14、 ，ABa，AEb，ACm，ADn（a，b，m，n 为常数） ，S ABC： S ADE是否为定值？如果是，用含 a，b，m，n 的式子表示此定值（直接写出结论，不写推理过程） ，如果不 是，说明理由 （图） 5 （解决问题）如图 1，在中，于点点是边上任意一点，过ABC10ABACCGABGPBC 点作，垂足分别为点，点 （1）若，则的面积是_，_ （2）猜想线段，的数量关系，并说明理由 （3）（变式探究） 如图 2， 在中， 若， 点是内任意一点， 且， ，垂足分别为点，点，点，求的值 （4） （拓展延伸）如图 3，将长方形沿折叠，使点落在点上，点落在点处，点为 折痕上的任意一点， 过点作
15、， 垂足分别为点， 点 若， 直接写出的值 6如图，已知锐角 ABC 中，AB、AC 边的中垂线交于点 O PPEABPFACEF 3PE 5PF ABPCG PEPFCG ABC10ABACBCPABCPEBC PFACPGABEFGPEPFPG ABCDEFDBC C P EFPPGBEPHBCGH8AD3CF PGPH （1）若A=（0 90 ） ，求BOC； （2）试判断ABO+ACB 是否为定值；若是，求出定值，若不是，请说明理由 7 O 的直径 AB15cm， 有一条定长为 9cm 的动弦， CD 在弧 AB 上滑动 （点 C 和 A、 点 D 与 B 不重合） ， 且 CECD
16、交 AB 于 E，DFCD 交 AB 于 F （1）求证：AEBF （2）在动弦 CD 滑动过程中，四边形 CDFE 的面积是否为定值，若是定值，请给出证明，并求这个定值， 若不是，请说明理由. 8 如图， 动点在以为圆心，为直径的半圆弧上运动 （点 不与点及的中点重合） ， 连接.过点作于点，以为边在半圆同侧作正方形，过点作的切线 交射线于点，连接、. （1）探究：如左图，当动点在上运动时； 判断是否成立？请说明理由； 设 ，是否为定值？若是，求出该定值，若不是，请说明理由； 设， 是否为定值？若是，求出该定值，若不是，请说明理由； （2）拓展：如右图，当动点在上运动时； 分别判断（1）中的
17、三个结论是否保持不变？如有变化，请直接写出正确的结论.（均不必说明理由） 9 如图， 已知的半径为，为直径，为弦与交于点， 将 沿着翻折后， 点与圆心重合，延长至，使，链接 （ ）求的长 （）求证：是的切线 （） 点为的中点， 在延长线上有一动点， 连接交于点， 交于点（与、 不重合） 则为一定值请说明理由，并求出该定值 10在平面直角坐标系中，点 A 和点 B 分别在 x 轴的正半轴和 y 轴的正半轴上，且 OA=6，OB=8，点 D 是 AB 的中点 （1）直接写出点 D 的坐标及 AB 的长； （2） 若直角NDM 绕点 D 旋转， 射线 DP 分别交 x 轴、 y 轴于点 P、 N，
18、射线 DM 交 x 轴于点 M， 连接 MN 当点 P 和点 N 分别在 x 轴的负半轴和 y 轴的正半轴时，若 PDMMON，求点 N 的坐标； 在直角NDM 绕点 D 旋转的过程中，DMN 的大小是否会发生变化？请说明理由 11如图， AOB 中，A（8，0） ，B（0，） ，AC 平分OAB，交 y 轴于点 C，点 P 是 x 轴上一点，P 经过点 A、C，与 x 轴于点 D，过点 C 作 CEAB，垂足为 E，EC 的延长线交 x 轴于点 F， （1）P 的半径为 ； （2）求证：EF 为P 的切线； （3）若点 H 是上一动点，连接 OH、FH，当点 H 在上运动时，试探究是否为定值
19、？若为定 值，求其值；若不是定值，请说明理由. O2ABCDABCDM CD CD AOOAPAPOAPC 1CD 2PCO 3G ADB PC QQG ABE BC FFB CGE GF 32 3 CDCD OH FH 12如图，在菱形 ABCD 中，ABC60 ，AB2过点 A 作对角线 BD 的平行线与边 CD 的延长线相交 于点 EP 为边 BD 上的一个动点（不与端点 B，D 重合） ，连接 PA，PE，AC （1）求证：四边形 ABDE 是平行四边形； （2）求四边形 ABDE 的周长和面积； （3）记 ABP 的周长和面积分别为 C1和 S1， PDE 的周长和面积分别为 C2和
20、 S2，在点 P 的运动过程中， 试探究下列两个式子的值或范围：C1+C2，S1+S2，如果是定值的，请直接写出这个定值；如果不是定值 的，请直接写出它的取值范围 13如图，在中，圆心关于弦的对称点恰好在 上，连接、. （1）求证：四边形是菱形； （2）如图，若点是优弧（不含端点、）上任意一点，连接交于点，的半径为 . 试探究 线段与的积 是否为定值？若是，求出该定值；若不是，请说明理由； 求的取值范围. OOABCOACBCBOAO AOBC Q AmB AB CQ ABPO 2 3 CP CQCP CQ CPPO 14如图，抛物线的顶点坐标为 C（0，8） ，并且经过 A（8，0） ，点
21、P 是抛物线上点 A，C 间的一个动点（含 端点） ，过点 P 作直线 y=8 的垂线，垂足为点 F，点 D，E 的坐标分别为（0，6） ， （4，0） ，连接 PD，PE， DE （1）求抛物线的解析式； （2）猜想并探究：对于任意一点 P，PD 与 PF 的差是否为固定值？如果是，请求出此定值；如果不是，请 说明理由； （3）求：当 PDE 的周长最小时的点 P 坐标；使 PDE 的面积为整数的点 P 的个数 15如图 1，点、，其中、满足 ，将点、分别向上平移 2 个单位，再向右平移 1 个单位至、，连接、. （1）直接写出点的坐标：_； ,0A a ( ,0)B ba b 2 340a
22、bbaAB CDACBD D （2）连接交于一点，求的值： （3）如图 2，点从点出发，以每秒 1 个单位的速度向上平移运动，同时点从点出发，以每秒 2 个单位的速度向左平移运动，设射线交轴于.问的值是否为定值？如果是定值，请 求出它的值；如果不是定值，请说明理由. 16如图所示，为等腰底边上一动点， 于于， ， 问当点在边上运动时，的值是否为定值， 如果是， 求出这个定值， 如果不是，说明理由 17如图，在平面直角坐标系中，已知直线和与轴分别相交于点和点，设两直 线相交于点，点为的中点，点是线段上一个动点（不与点和重合） ，连结，并过 点作交于点 （ ）判断的形状，并说明理由 （）当点在线段
23、上运动时，四边形的面积是否为定值？若是，请求出这个定值；若不是， 请说明理由 （）当点的横坐标为时，在轴上找到一点使得的周长最小，请直接写出点的坐标 类型一 【线段及线段的和差为定值】 【典例指引 1】 已知： ABC 是等腰直角三角形， BAC90 ， 将ABC 绕点 C 顺时针方向旋转得到ABC， 记旋转角为 ，当 90 180 时，作 ADAC，垂足为 D，AD 与 BC 交于点 E ADOCF CF OF MONB DN y F FMDOFN SS DABCBCDEAB ,E DFAC F 8,24 ABC ACcm SDCDEDF 2yx6yx x AB CDABEACACDE DD
24、FDEBCF 1ABC 2EACCEDF 3E 1 2 xPPEFP （1）如图 1，当CAD15 时，作AEC 的平分线 EF 交 BC 于点 F 写出旋转角 的度数； 求证：EA+ECEF； （2）如图 2，在（1）的条件下，设 P 是直线 AD 上的一个动点，连接 PA，PF，若 AB 2，求线段 PA+PF 的最小值 （结果保留根号） 【答案】 （1）105 ，见解析； （2） 62 6 【解析】 （1）解直角三角形求出ACD 即可解决问题， 连接 AF，设 EF 交 CA于点 O，在 EF 时截取 EM=EC，连接 CM首先证明CFA是等边三角形，再证明 FCMACE（SAS） ，即
25、可解决问题 （2） 如图 2 中， 连接 AF， PB， AB， 作 BMAC 交 AC 的延长线于 M 证明AEFAEB， 推出 EF=EB， 推出 B，F 关于 AE 对称，推出 PF=PB，推出 PA+PF=PA+PBAB，求出 AB即可解决问题 【详解】 解： 由CAD15 ， 可知ACD=90 -15 =75 ， 所以ACA=180 -75 =105 即旋转角 为 105 证明：连接 AF，设 EF 交 CA于点 O在 EF 时截取 EMEC，连接 CM CEDACE+CAE45 +15 60 ， CEA120 ， FE 平分CEA， CEFFEA60 ， FCO180 45 75
26、60 ， FCOAEO，FOCAOE， FOCAOE， OF A O OC OE ， OF OC AO OE ， COEFOA， COEFOA， FAOOEC60 ， ACF 是等边三角形， CFCAAF， EMEC，CEM60 ， CEM 是等边三角形， ECM60 ，CMCE， FCAMCE60 ， FCMACE， FCMACE（SAS） ， FMAE， CE+AEEM+FMEF （2）解：如图 2 中，连接 AF，PB，AB，作 BMAC 交 AC 的延长线于 M 由可知，EAFEAB75 ，AEAE，AFAB， AEFAEB， EFEB， B，F 关于 AE 对称， PFPB， PA+
27、PFPA+PBAB， 在 RtCBM 中，CBBC 2AB2，MCB30 ， BM 1 2 CB1，CM3， AB 22 AMB M 22 ( 23)1 62 6 PA+PF 的最小值为 62 6 【名师点睛】 本题属于四边形综合题，考查旋转变换相关，全等三角形的判定和性质，相似三角形的判定和性质以及三 角形的三边关系等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思 想思考问题，属于中考压轴题，难度较大 【举一反三】 如图（1） ，已知=90MON,点P为射线ON上一点，且=4OP，B、C为射线OM和ON上的两个动点 （OCOP） ，过点P作PABC，垂足为点A，
28、且=2PA，联结BP （1）若 1 2 PAC ABOP S S 四边形 时，求tan BPO的值； （2）设PCx， AB y BC 求y与x之间的函数解析式，并写出定义域； （3）如图(2)，过点A作BP的垂线，垂足为点H，交射线ON于点Q，点B、C在射线OM和ON上运动 时， 探索线段OQ的长是否发生变化？若不发生变化， 求出它的值。 若发生变化， 试用含 x 的代数式表示OQ 的长 【答案】 （1） 3 tan 2 OB OPB OP ； （2） 2 44 4 x y xx (x2)； （3）OQ 的长度等于 3. 【解析】 （1）根据有两对角相等的三角形相似可证明CAPCOB，由相似
29、三角形的性质可知： 2 () PAC COB AP OB S S ，在由已知条件可求出 OB 的长，由正切的定义计算即可； （2）作 AEPC 于 E，易证PAEPCA，根据相似三角形的性质：对应边的比值相等 4 PE x ，再利用 平行线的性质即可得到 AB OE BCOC ，所以 4 4 4 x y x ，整理即可得到求 y 与 x 之间的函数解析式，并写出 定义域即可； （3） 点 B、 C 在射线 OM 和 ON 上运动时， 探索线段 OQ 的长不发生变化， 由PAHPBA 得： PAPH PBPA ， 即 PA 2=PHPB，由PHQPOB 得： PQPH PBPO 即 PQPO=P
30、HPB，所以 PA 2 =PQPO，再由已知数据 即可求出 OQ 的长 【详解】 （1）ACP=OCB CAP=O=90 CAPCOB 2 () PAC COB AP OB S S 1 2 PAC ABOP S S 四边形 1 3 PAC COB S S 2 1 () 3 AP OB AP=2 2 3OB 在 RtOBP 中， 3 tan 2 OB OPB OP （2）作 AEPC，垂足为 E， 易证PAEPCA PA PE PCPA 2 2PE x 4 PE x MON=AEC=90 AEOM ABOE BCOC 4 4 4 x y x 整理得 2 44 4 x y xx (x2) （3）线
31、段 OQ 的长度不会发生变化 由PAHPBA 得 PAPH PBPA 即 2 PAPH PB 由PHQPOB 得 PQPH PBPO 即PQ POPH PB 2 PAPQ PO PA=2 PO=4 PQ=1 OQ=3 即 OQ 的长度等于 3. 【点睛】 此题考查相似形综合题，解题关键在于作辅助线 类型二 【线段的积或商为定值】 【典例指引 2】 如图， 矩形ABCD中，2,5,1ABBCBP， 0 90MPN， 将M P N绕点P从PB 处开始按顺时针方向旋转，PM交边AB（或AD）于点E，PN交边AD（或CD）于点F.当PN旋转 至PC处时，MPN的旋转随即停止. （1）特殊情形：如图，发
32、现当PM过点A时，PN也恰好过点D，此时ABP是否与PCD相似？并 说明理由； （2）类比探究：如图，在旋转过程中， PE PF 的值是否为定值？若是，请求出该定值；若不是，请说明理 由； （3）拓展延伸：设AEt时，EPF的面积为S，试用含t的代数式表示S； 在旋转过程中，若1t 时，求对应的EPF的面积； 在旋转过程中，当EPF的面积为 4.2 时，求对应的t的值. 【答案】 （1）相似； （2）定值， 1 2 PE PF ； （3）2， 4 5 2 5 t . 【解析】 （1）根据“两角相等的两个三角形相似”即可得出答案； （2）由EBPPGF得出 PEBP PFGF ，又2,1FGAB
33、BP为定值，即可得出答案； （3）先设,2AEt BEt结合 EPFAEFBEPPFGABGF SSSSS 矩形 得出 2 45Stt将 t=1 代入 2 45Stt中求解即可得出答案； 将 s=4.2 代入 2 45Stt中求解即可得出答案. 【详解】 （1）相似 理由： 0 90BAPBPA， 0 90CPDBPA， BAPCPD， 又 0 90ABPPCD ， ABPPCD； （2） 在旋转过程中 PE PF 的值为定值， 理由如下：过点F作FGBC于点G，BEPGPF， 0 90EBPPGF ，EBPPGF， PEBP PFGF ， 四边形ABCD为矩形，四边形ABGF为矩形， 2,1
34、FGABBP 1 2 PE PF 即在旋转过程中， PE PF 的值为定值， 1 2 PE PF ； （3）由（2）知：EBPPGF， 1 2 BEPE PGPF ， 又,2AEt BEt， 2 242PBtt，1425 2BGAFBPPGtt ， EPFAEFBEPPFGABGF SSSSS 矩形 2 111 2 52521224245 222 ttttttt 即： 2 45Stt； 当1t 时，EPF的面积 2 14 1 52S ， 当4.2 EPF S时， 2 454.2tt 解得： 1 4 5 2 5 t ， 2 4 5 2 5 t （舍去） 当EPF的面积为 4.2 时， 4 5 2
35、 5 t ； 【名师点睛】 本题考查的是几何综合，难度系数较高，涉及到了相似以及矩形等相关知识点，第三问解题关键在于求出 面积与 AE 的函数关系式. 【举一反三】 如图 1,已知直线 ya 与抛物线 2 1 4 yx交于 A、B 两点(A 在 B 的左侧),交 y 轴于点 C (1)若 AB4,求 a 的值 (2)若抛物线上存在点 D(不与 A、B 重合),使 1 2 CDAB,求 a 的取值范围 (3)如图2,直线ykx2与抛物线交于点E、 F,点P是抛物线上的动点,延长PE、 PF分别交直线y2于M、 N 两点,MN 交 y 轴于 Q 点,求 QM QN 的值。 图 1 图 2 【答案】
36、 （1）1a ； （2）4a； （3）8 【解析】 （1）将两个函数解析式联立，解一元二次方程求得 A、B 的横坐标，进而表示出 AB，即可解答； （2）由（1）可得 CD= 1 2 AB=2 a，设 D( 4,)m m ，过点 D 作 DHy 轴于点 H，利用勾股定理可知 222 DHCHCD，进而得到( )(4)0ma ma ，得到40m a ，根据函数图象可知0m ，即 可求得 a 的取值范围； （3）设 E（ 2 11 1 , 4 xx） ，F（ 2 22 1 , 4 xx） ，P（ 2 1 , 4 nn） ，分别表示 EP 和 FP 的解析式，当2y 时，求得 1 1 8 M nx
37、x nx ， 2 2 8 N nx x nx ，联立 2 1 4 yx和 ykx2，得到 2 1 20 4 xkx，利用一元二次方程根与 系数的关系得到 121 2 4 ,8xxk x x ，代入 MN QM QNxx 即可解答. 【详解】 （1）联立 2 1 4 yx ya ， 2 1 4 xa，解得： 12 2,2xa xa 44 BA ABxxa 1a （2）由（1）知 AB=4 a， CD= 1 2 AB=2 a 设 D( 4 ,)m m 过点 D 作 DHy 轴于点 H，则 222 DHCHCD 22 ( 4)()4mama ()(4)0ma ma 又ma 40m a 4ma 又0m
38、 40a 4a （3）设 E（ 2 11 1 , 4 xx） ，F（ 2 22 1 , 4 xx） ，P（ 2 1 , 4 nn） EP 解析式为y txb 将 P，E 代入可得： 11 11 () 44 ynx xnx 当2y 时，可求 1 1 8 M nx x nx ， 同理可求 FP 的解析式为 22 11 () 44 ynx xnx 2 2 8 N nx x nx 又联立 2 1 4 2 yx ykx 得： 2 1 20 4 xkx 121 2 4 ,8xxk x x 2 121212 2 121212 888 ()64 () MN nxnxn x xn xx QM QNxx nxnx
39、nn xxx x 2 2 88464 8 48 nnk nnk 【点睛】 本题为二次函数与一次函数综合题，难度大，主要考查二次函数与一次函数交点问题，还涉及了一元二次 方程和勾股定理等知识，熟练掌握一次函数与二次函数的性质和相关知识点是解题关键. 类型三 【角及角的和差定值】 【典例指引 3】如图，在ABC 中，ABC60 ，BAC60 ，以 AB 为边作等边ABD（点 C、D 在边 AB 的同侧） ，连接 CD （1）若ABC90 ，BAC30 ，求BDC 的度数； （2）当BAC2BDC 时，请判断ABC 的形状并说明理由； （3）当BCD 等于多少度时，BAC2BDC 恒成立 【答案】
40、（1）30 ； （2）ABC 是等腰三角形，理由见解析； （3）当BCD=150 时，BAC=2BDC 恒成立. 【解析】 （1）证明 AC 垂直平分 BD，从而可得 CD=BC，继而得BDC=30 ； （2）设BDC=x，则BAC=2x，证明ACD=ADC，从而得 AC=AD，再根据 AB=AD 可得 AB=AC，从而 得ABC 是等腰三角形； （3）如图， 作等边BCE，连接 DE，证明BCDECD 后可得到BDE=2BDC，再通过证明BDE BAC 得到BAC=BDE，从而得BAC=2BDC. 【详解】 （1）ABD 为等边三角形， BAD=ABD=60 ，AB=AD， 又BAC=30
41、， AC 平分BAD， AC 垂直平分 BD， CD=BC， BDC=DBC=ABC-ABD=90 -60 =30 ； （2）ABC 是等腰三角形， 理由：设BDC=x，则BAC=2x， 有CAD=60 -2x，ADC=60 +x， ACD=180 -CAD-ADC=60 +x， ACD=ADC， AC=AD， 又AB=AD， AB=AC， 即ABC 是等腰三角形； （3）当BCD=150 时，BAC=2BDC 恒成立， 如图， 作等边BCE，连接 DE， BC=EC，BCE=60 . BCD=150 ， ECD=360 -BCD-BCE=150 ， DCE=DCB. 又CD=CD， BCDE
42、CD. BDC=EDC， 即BDE=2BDC. 又ABD 为等边三角形， AB=BD，ABD=CBE=60 ， ABC=DBE=60 +DBC. 又BC=BE， BDEBAC. BAC=BDE， BAC=2BDC. 【名师点睛】 本题考查了等边三角形的性质、全等三角形的判定与性质等，熟练掌握和运用相关性质、结合图形正确添 加辅助线是解题的关键. 【举一反三】 如图 1，抛物线 2 : 2Wyax的顶点为点A，与x轴的负半轴交于点D，直线AB交抛物线 W 于另一点 C，点B的坐标为1,0 （1）求直线AB的解析式； （2）过点C作CEx轴，交x轴于点E，若AC平分DCE，求抛物线 W 的解析式；
43、 （3） 若 1 2 a ， 将抛物线 W 向下平移0m m个单位得到抛物线 1 W， 如图 2， 记抛物线 1 W的顶点为 1 A， 与x轴负半轴的交点为 1 D，与射线BC的交点为 1 C问：在平移的过程中， 11 tan DC B是否恒为定值？ 若是，请求出 11 tan DC B的值；若不是，请说明理由 【答案】 （1）22yx； （2） 2 25 2 32 yx； （3） 11 tan DC B恒为定值 1 3 【解析】 （1）由抛物线解析式可得顶点 A 坐标为（0，-2） ，利用待定系数法即可得直线 AB 解析式； （2）如图，过点B作BNCD于N，根据角平分线的性质可得 BE=B
44、N，由BND=CED=90 ，BND= CDE 可证明BNDCEDV: V，设 BE=x，BD=y，根据相似三角形的性质可得 CE=2x，CD=2y，根据勾股 定理由得 y 与 x 的关系式，即可用含 x 的代数式表示出 C、D 坐标，代入 y=ax2-2 可得关于 x、a 的方程组， 解方程组求出 a 值即可得答案； （3）过点B作BFCD于点F，根据平移规律可得抛物线 W1的解析式为 y= 1 2 x2-2-m，设点 1 D的坐标为 （t，0） （t0） ，代入 y= 1 2 x2-2-m 可得 2+m= 1 2 t2，即可的 W1的解析式为 y= 1 2 x2- 1 2 t2，联立直线 BC 解析式 可用含 t 的代数式表示出点 C1的坐标，即可得 11 C HD H，可得 11 45C D H o ，根据抛物线 W 的解析 式可得点D坐标， 联立直线BC与抛物线W的解析式可得点C、 A坐标， 即可求出CG、 DG的长， 可得CG=DG， CDG= 11 45C D H o ，即可证明 11/ / C DCD，可得 11 DC BDCB， 11 tan DC Btan DCB，由 CDG=45 可得 BF=DF，根据等腰三角形的性质可求出 DF 的长，利用勾股定理可求出 CD 的长，即可求 出 CF 的长，根据三角
