 重庆市八中2020年中考数学自主测试(含答案)
重庆市八中2020年中考数学自主测试(含答案)
《重庆市八中2020年中考数学自主测试(含答案)》由会员分享,可在线阅读,更多相关《重庆市八中2020年中考数学自主测试(含答案)(14页珍藏版)》请在七七文库上搜索。
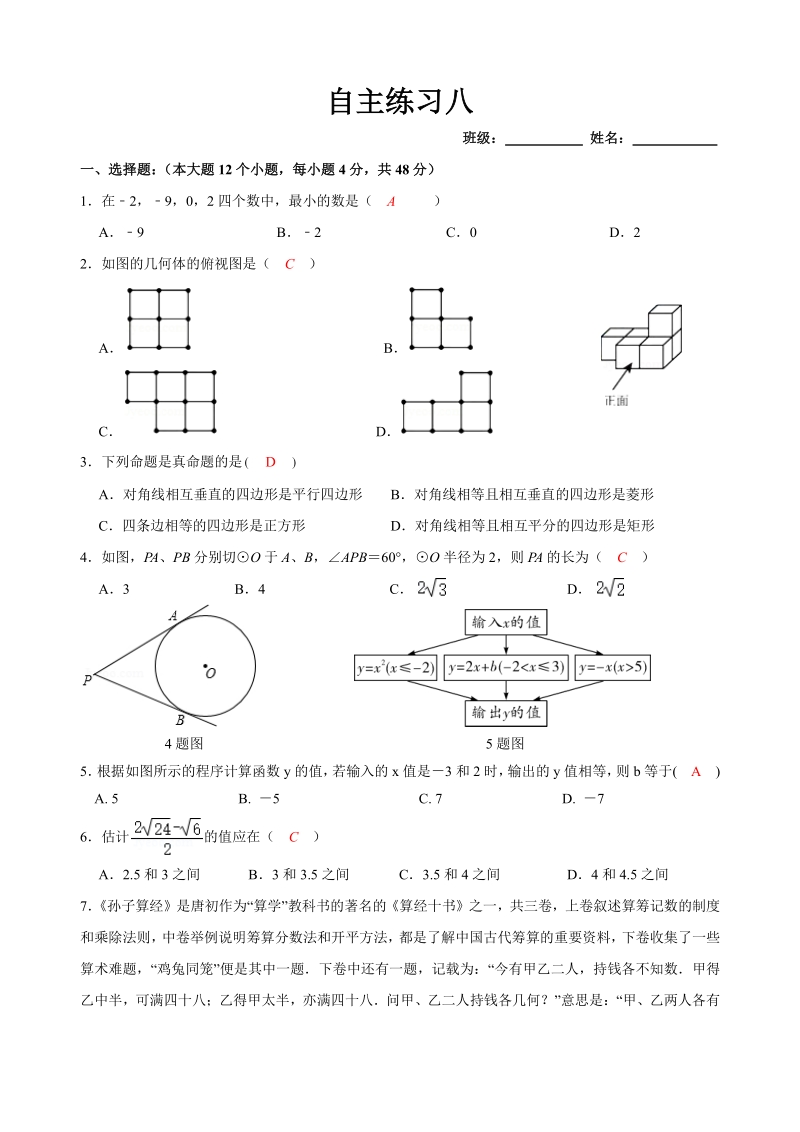
1、自主练习八自主练习八 班级:班级: 姓名:姓名: 一、选择题: (本大题一、选择题: (本大题 12 个小题,每小题个小题,每小题 4 分,共分,共 48 分)分) 1在2,9,0,2 四个数中,最小的数是( A ) A9 B2 C0 D2 2如图的几何体的俯视图是( C ) A B C D 3下列命题是真命题的是( D ) A对角线相互垂直的四边形是平行四边形 B对角线相等且相互垂直的四边形是菱形 C四条边相等的四边形是正方形 D对角线相等且相互平分的四边形是矩形 4如图,PA、PB 分别切O 于 A、B,APB60,O 半径为 2,则 PA 的长为( C ) A3 B4 C D 4 题图
2、5 题图 5 根据如图所示的程序计算函数 y 的值, 若输入的 x 值是3 和 2 时, 输出的 y 值相等, 则 b 等于( A ) A. 5 B. 5 C. 7 D. 7 6估计的值应在( C ) A2.5 和 3 之间 B3 和 3.5 之间 C3.5 和 4 之间 D4 和 4.5 之间 7 孙子算经是唐初作为“算学”教科书的著名的算经十书之一,共三卷,上卷叙述算筹记数的制度 和乘除法则, 中卷举例说明筹算分数法和开平方法, 都是了解中国古代筹算的重要资料, 下卷收集了一些 算术难题,“鸡兔同笼”便是其中一题下卷中还有一题,记载为:“今有甲乙二人,持钱各不知数甲得 乙中半,可满四十八;
3、乙得甲太半,亦满四十八问甲、乙二人持钱各几何?”意思是:“甲、乙两人各有 若干钱,如果甲得到乙所有钱的一半,那么甲共有钱 48 文如果乙得到甲所有钱的 2 3 ,那么乙也共有钱 48 文问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( A ) A 1 48 2 2 48 3 xy yx += += B 1 48 2 2 48 3 yx xy += += C 1 48 2 2 48 3 xy yx = = D 1 48 2 2 48 3 yx xy = = 8 如图,等腰 RtABC 与等腰 RtCDE 是以点 O 为位似中心的位似图形,位似比为 k1:3,ACB 90,
4、BC4,则点 D 的坐标是( A ) A (18,12) B (16,12) C (12,18) D (12,16) 9在课外实践中,小明为了测量江中信号塔 A 离河边的距离 AB,采取了如下措施:如图在江边 D 处, 测得信号塔 A 的俯角为 40,若 DE55 米,DECE,CE36 米,CE 平行于 AB,BC 的坡度为 i1: 0.75,坡长 BC140 米,则 AB 的长为( C ) (精确到 0.1 米,参考数据:sin400.64,cos400.77, tan400.84) A78.6 米 B78.7 米 C78.8 米 D78.9 米 10如图,在平面直角坐标系中,正方形ABC
5、D的顶点A的坐标为( 1,1),点B在x轴正半轴上,点D在 第三象限的双曲线 8 y x =上,过点C作/ /CEx轴交双曲线于点E,则CE的长为( B ) A 8 5 B 23 5 C3.5 D5 11若关于 x 的不等式组 + + 2 3 1 3 1 0 3 xx xa 至少有六个整数解,且关于 y 的分式方程 的解为整数,则符合条件的所有整数 a 有( B )个 A.0 B.1 C.2 D.3 12如图,在矩形 ABCD 中,AB1,BCa,点 E 在边 BC 上,且 BE a连接 AE,将ABE 沿 AE 折叠,若点 B 的对应点 B落在矩 形 ABCD 的边上,则 a 的值为( C
6、) y ay y =+ 2 1 2 2 9 题图 10 题图 8 题图 A 5 3 B 3 5 C 5 3 或 5 3 D 3 5 或 5 3 【解答】解:分两种情况: 当点 B落在 AD 边上时,如图 1四边形 ABCD 是矩形, BADB90, 将ABE 沿 AE 折叠,点 B 的对应点 B落在 AD 边上, BAEBAEBAD45,ABBE, a1,a; 当点 B落在 CD 边上时,如图 2 四边形 ABCD 是矩形,BADBCD90,ADBCa 将ABE 沿 AE 折叠,点 B 的对应点 B落在 CD 边上, BABE90,ABAB1,EBEBa, DB,ECBCBEaaa 在ADB与
7、BCE 中, , ADBBCE,即, 解得 a1,a2(舍去) 综上,所求 a 的值为或 二填空题: (本大题二填空题: (本大题 6 个小题,每小题个小题,每小题 4 分,共分,共 24 分)分) 13计算: () 0 2 1) 2 2 (- 3 14若分式 2 4 2 a a + 的值为 0,则 a 的值为 2 15从某油菜籽种子在相同条件下发芽试验的结果如下: 每批粒数 100 400 800 1000 2000 4000 发芽的频数 85 298 652 793 1604 3204 发芽的频率 0.850 0.745 0.815 0.793 0.802 0.801 根据以上数据可以估计
8、,该油菜籽种子发芽的概率为 0.8 .(精确到0.1) 16 如图,Rt ABC中,90A=,4AB =,6AC =,D、E分别是AB、AC边上的动点, 且3CEBD=, 则BDE面积的最大值为 3 2 16 题图 17 题图 17已知 A、B、C 三地顺次在同一直线上,甲、乙两人均骑车从 A 地出发,向 C 地匀速行驶甲比乙早 出发 5 分钟,甲到达 B 地并休息了 2 分钟后,乙追上了甲甲、乙同时从 B 地以各自原速继续向 C 地 行驶当乙到达 C 地后,乙立即掉头并提速为原速的倍按原路返回 A 地,而甲也立即提速为原速的 倍继续向 C 地行驶,到达 C 地就停止若甲、乙间的距离 y(米)
9、与甲出发的时间 t(分)之间的函 数关系如图所示,则当甲到达 C 地时,乙距 A 地 6075 米 解:由题意可得,甲乙两人刚开始的速度之差为:900(2314)100(米/分) , 设甲刚开始的速度为 x 米/分,乙刚开始的速度为(x+100)米/分, 12x(145)(x+100) ,解得,x300,则 x+100400, 则 A、B 两地之间的距离为:300123600(米) , A、C 两地之间的距离为:400(235)7200(米) , 当乙到达 C 地后,乙立即掉头并提速为原速的倍按原路返回 A 地,而甲也立即提速为原速的倍继续向 C 地行驶, 后来乙的速度为:400500(米/分
10、) ,甲的速度为 300400(米/分) , 甲到达 C 地的时间为:23+7200(232)30040025(分钟) , 当甲到达 C 地时,乙距 A 地:7200(2523)5006075(米) , 故答案为:6075 18 一副含 30和 45角的三角板 ABC 和 DEF 叠合在一起, 边 BC 与 EF 重合, BCEF12cm (如图 1) , 点 G 为边 BC(EF)的中点,边 FD 与 AB 相交于点 H,现将三角板 DEF 绕点 G 按顺时针方向旋转 (如图 2) ,在CGF 从 0到 60的变化过程中,点 H 相应移动的路径长共为 (1218) (结 果保留根号) 【解答
11、】解:如图 1 中,作 HMBC 于 M,设 HMa,则 CMHMa 在 RtABC 中,ABC30,BC12, 在 RtBHM 中,BH2HM2a,BMa, BM+FMBC, a+a12, a66, BH2a1212 如图 2 中,当 DGAB 时,易证 GH1DF,此时 BH1的值最小,易知 BH1BK+KH13+3, HH1BHBH1915, 当旋转角为 60时,F 与 H2重合,易知 BH26, 观察图象可知,在CGF 从 0到 60的变化过程中,点 H 相应移动的路径长2HH1+HH218 30+6(1212)1218 故答案为(1218)cm 三解答题(共三解答题(共 8 小题小题
12、,共,共 78 分)分) 19 (8)计算: (1) (2xy)2(xy) (4xy) (2) 【解答】解: (1)原式4x24xy+y2(4x2xy4xy+y2) 4x24xy+y24x2+5xyy2 xy4 (2)原式 8 20 (10)如图,O 为等边ABC 的外接圆,ADBC,ADC90,CD 交O 于点 E (1)求证:AD 是O 的切线; (2)若 DE2,求阴影部分的面积 【解答】 (1)证明:连接 AO 并延长交 BC 于 F,如图所示: 则 AFBC,AFC90, ADBC,ADC90,BCD180ADC90, 四边形 AFCD 是矩形,DAF90,AFCD, ADOA,AD
13、 是O 的切线;5 (2)解:连接 AE、OE,如图 2 所示: 由(1)得:AFCD, ACDCAFBAC30,AOE2ACD60, OAOE,AOE 是等边三角形, OAAE,OAE60,DAE30,ADC90, OAAE2DE4,ADDE2, 阴影部分的面积梯形 OADE 的面积扇形 AOE 的面积 (2+4)2610 21(10) 为了增强学生对新冠病毒预防知识的了解, 我校初一年级开展了网上预防知识的宣传教育活动。 为了解这次宣传教育活动的效果,学校从初一年级 1500 名学生中随机抽取部分学生进行网上知识测试 (测试满分 100 分,得分均为整数) ,并根据抽取的学生测试成绩,制作


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 重庆市 2020 年中 数学 自主 测试 答案
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-134389.html