1、 2020 年湖北省宜昌市近三年中考真题数学重组模拟卷（二）年湖北省宜昌市近三年中考真题数学重组模拟卷（二） 一选择题（下列各小题中，只有一个选项是符合题目要求的，请在答题卡上指定的位置一选择题（下列各小题中，只有一个选项是符合题目要求的，请在答题卡上指定的位置 填涂符合要求的选项前的字母代号，每题填涂符合要求的选项前的字母代号，每题 3 分，计分，计 45 分）分） 1 （2017宜昌）有理数的倒数为（ ） A5 B C D5 2 （2018宜昌）如下字体的四个汉字中，是轴对称图形的是（ ） A B C D 3 （2017宜昌）如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“爱”字
2、 一面的相对面上的字是（ ） A美 B丽 C宜 D昌 4 （2018宜昌）计算 4+（2）25（ ） A16 B16 C20 D24 5 （2019宜昌）在纳木错开展的第二次青藏高原综合科学考查研究中，我国自主研发的系 留浮空器于 5 月 23 日凌晨达到海拔 7003 米的高度这一高度也是已知的同类型同量级 浮空器驻空高度的世界纪录数据 7003 用科学记数法表示为（ ） A0.7104 B70.03102 C7.003103 D7.003104 6 （2017宜昌）九一（1）班在参加学校 4100m 接力赛时，安排了甲，乙，丙，丁四位 选手，他们的顺序由抽签随机决定，则甲跑第一棒的概率为（
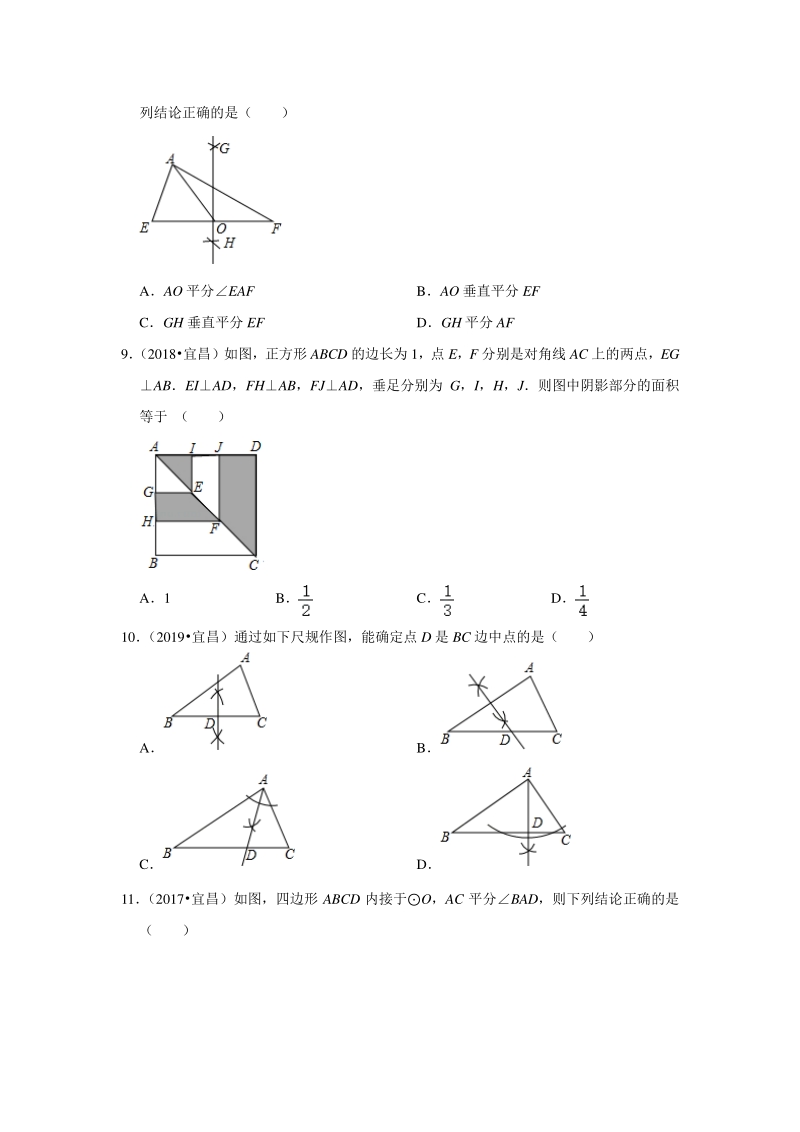
3、 ） A1 B C D 7 （2019宜昌）下列计算正确的是（ ） A3ab2ab1 B （3a2）29a4 Ca6a2a3 D3a22a6a2 8 （2017宜昌）如图，在AEF 中，尺规作图如下：分别以点 E，点 F 为圆心，大于EF 的长为半径作弧，两弧相交于 G，H 两点，作直线 GH，交 EF 于点 O，连接 AO，则下 列结论正确的是（ ） AAO 平分EAF BAO 垂直平分 EF CGH 垂直平分 EF DGH 平分 AF 9 （2018宜昌）如图，正方形 ABCD 的边长为 1，点 E，F 分别是对角线 AC 上的两点，EG ABEIAD，FHAB，FJAD，垂足分别为 G，
4、I，H，J则图中阴影部分的面积 等于 （ ） A1 B C D 10 （2019宜昌）通过如下尺规作图，能确定点 D 是 BC 边中点的是（ ） A B C D 11 （2017宜昌）如图，四边形 ABCD 内接于O，AC 平分BAD，则下列结论正确的是 （ ） AABAD BBCCD C DBCADCA 12 （2018宜昌）如图，直线 AB 是O 的切线，C 为切点，ODAB 交O 于点 D，点 E 在O 上，连接 OC，EC，ED，则CED 的度数为（ ） A30 B35 C40 D45 13 （2019宜昌） 古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边 求面积的公
5、式，称为海伦秦九韶公式：如果一个三角形的三边长分别是 a，b，c，记 p ，那么三角形的面积为 S如图，在ABC 中，A， B，C 所对的边分别记为 a，b，c，若 a5，b6，c7，则ABC 的面积为（ ） A6 B6 C18 D 14 （2018宜昌）如图，要测量小河两岸相对的两点 P，A 的距离，可以在小河边取 PA 的 垂线 PB 上的一点 C，测得 PC100 米，PCA35，则小河宽 PA 等于（ ） A100sin35米 B100sin55米 C100tan35米 D100tan55米 15 （2018宜昌）如图，一块砖的 A，B，C 三个面的面积比是 4：2：1如果 A，B，C
6、 面 分别向下放在地上，地面所受压强为 p1，p2，p3，压强的计算公式为 p，其中 P 是压 强，F 是压力，S 是受力面积，则 p1，p2，p3，的大小关系正确的是（ ） Ap1p2p3 Bp1p3p2 Cp2p1p3 Dp3p2p1 二解答题（本大题共有二解答题（本大题共有 9 个小题，共个小题，共 75 分）分） 16 （2019宜昌）已知：xy，yx+8，求代数式+的值 17 （2018宜昌）解不等式组，并把它的解集在数轴上表示出来 18 （2017宜昌）YC 市首批一次性投放公共自行车 700 辆供市民租用出行，由于投入数量 不够，导致出现需要租用却未租到车的现象，现将随机抽取的某
7、五天在同一时段的调查 数据汇成如下表格 请回答下列问题： 时间 第一天 7：00 8：00 第二天 7：00 8：00 第三天 7：00 8：00 第四天 7：00 8：00 第五天 7：00 8：00 需要租用自行 车却未租到车 的人数（人） 1500 1200 1300 1300 1200 （1）表格中的五个数据（人数）的中位数是多少？ （2）由随机抽样估计，平均每天在 7：008：00 需要租用公共自行车的人数是多少？ 19 （2019宜昌） 人民日报 点赞湖北宜昌 “智慧停车平台” 作为 “全国智慧城市” 试点， 我市通过“互联网” 、 “大数据”等新科技，打造“智慧停车平台” ，着力
8、化解城市“停车 难”问题市内某智慧公共停车场的收费标准是：停车不超过 30 分钟，不收费；超过 30 分钟，不超过 60 分钟，计 1 小时，收费 3 元；超过 1 小时后，超过 1 小时的部分按每小 时 2 元收费（不足 1 小时，按 1 小时计） （1） 填空： 若市民张先生某次在该停车场停车 2 小时 10 分钟， 应交停车费 元 若 李先生也在该停车场停车，支付停车费 11 元，则停车场按 小时（填整数）计时 收费 （2）当 x 取整数且 x1 时，求该停车场停车费 y（单位：元）关于停车计时 x（单位： 小时）的函数解析式 20 （2018宜昌）某校创建“环保示范学校” ，为了解全校
9、学生参加环保类杜团的意愿，在 全校随机抽取了 50 名学生进行问卷调查，问卷给出了五个社团供学生选择（学生可根据 自己的爱好选择一个社团，也可以不选） ，对选择了社团的学生的问卷情况进行了统计， 如表： 社团名称 A酵素制作 社团 B 回收材料小 制作社团 C垃圾分类 社团 D环保义工 社团 E 绿植养护社 团 人数 10 15 5 10 5 （1）填空：在统计表中，这 5 个数的中位数是 ； （2）根据以上信息，补全扇形图（图 1）和条形图（图 2） ； （3）该校有 1400 名学生，根据调查统计情况，请估计全校有多少学生愿意参加环保义 工社团； （4）若小诗和小雨两名同学在酵素制作社团或
10、绿植养护社团中任意选择一个参加，请用 树状图或列表法求出这两名同学同时选择绿植养护社团的概率 21 （2019宜昌）如图，点 O 是线段 AH 上一点，AH3，以点 O 为圆心，OA 的长为半径 作O，过点 H 作 AH 的垂线交O 于 C，N 两点，点 B 在线段 CN 的延长线上，连接 AB 交O 于点 M，以 AB，BC 为边作ABCD （1）求证：AD 是O 的切线； （2）若 OHAH，求四边形 AHCD 与O 重叠部分的面积； （3）若 NHAH，BN，连接 MN，求 OH 和 MN 的长 22 （2017宜昌）某市总预算 a 亿元用三年时间建成一条轨道交通线轨道交通线由线路敷 设
11、、搬迁安置、辅助配套三项工程组成从 2015 年开始，市政府在每年年初分别对三项 工程进行不同数额的投资 2015 年年初，对线路敷设、搬迁安置的投资分别是辅助配套投资的 2 倍、4 倍随后两 年，线路敷设投资每年都增加 b 亿元，预计线路敷设三年总投资为 54 亿元时会顺利如期 完工；搬迁安置投资从 2016 年年初开始逐年按同一百分数递减，依此规律，在 2017 年 年初只需投资 5 亿元，即可顺利如期完工；辅助配套工程在 2016 年年初的投资在前一年 基础上的增长率是线路敷设 2016 年投资增长率的 1.5 倍， 2017 年年初的投资比该项工程 前两年投资的总和还多 4 亿元，若这
12、样，辅助配套工程也可以如期完工经测算，这三 年的线路敷设、辅助配套工程的总投资资金之比达到 3：2 （1）这三年用于辅助配套的投资将达到多少亿元？ （2）市政府 2015 年年初对三项工程的总投资是多少亿元？ （3）求搬迁安置投资逐年递减的百分数 23 （2018宜昌） 在矩形 ABCD 中， AB12， P 是边 AB 上一点， 把PBC 沿直线 PC 折叠， 顶点 B 的对应点是点 G，过点 B 作 BECG，垂足为 E 且在 AD 上，BE 交 PC 于点 F （1）如图 1，若点 E 是 AD 的中点，求证：AEBDEC； （2）如图 2，求证：BPBF； 当 AD25，且 AEDE
13、时，求 cosPCB 的值； 当 BP9 时，求 BEEF 的值 24 （2019宜昌）在平面直角坐标系中，正方形 ABCD 的四个顶点坐标分别为 A（2，4） ， B（2，2） ，C（4，2） ，D（4，4） （1）填空：正方形的面积为 ；当双曲线 y（k0）与正方形 ABCD 有四个交 点时，k 的取值范围是： ； （2）已知抛物线 L：ya（xm）2+n（a0）顶点 P 在边 BC 上，与边 AB，DC 分别 相交于点 E，F，过点 B 的双曲线 y（k0）与边 DC 交于点 N 点 Q（m，m22m+3）是平面内一动点，在抛物线 L 的运动过程中，点 Q 随 m 运 动，分别求运动过程
14、中点 Q 在最高位置和最低位置时的坐标； 当点 F 在点 N 下方，AENF，点 P 不与 B，C 两点重合时，求的值； 求证：抛物线 L 与直线 x1 的交点 M 始终位于 x 轴下方 2020 年湖北省宜昌市近三年中考真题数学重组模拟卷（二）年湖北省宜昌市近三年中考真题数学重组模拟卷（二） 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 15 小题）小题） 1 【解答】解：根据倒数的定义可知：的倒数为5 故选：D 2 【解答】解：A、不是轴对称图形，故本选项不符合题意； B、不是轴对称图形，故本选项不符合题意； C、不是轴对称图形，故本选项不符合题意； D、是轴对称图形，故
15、本选项符合题意； 故选：D 3 【解答】解：正方体的表面展开图，相对的面之间一定相隔一个正方形， 有“爱”字一面的相对面上的字是宜 故选：C 4 【解答】解：4+（2）25 4+45 4+20 24， 故选：D 5 【解答】解：将 7003 用科学记数法表示为：7.003103 故选：C 6 【解答】解：甲跑第一棒的概率为 故选：D 7 【解答】解：A、3ab2abab，故此选项错误； B、 （3a2）29a4，正确； C、a6a2a4，故此选项错误； D、3a22a6a3，故此选项错误 故选：B 8 【解答】解：由题意可得，GH 垂直平分线段 EF 故选：C 9 【解答】解：四边形 ABCD
16、 是正方形， 直线 AC 是正方形 ABCD 的对称轴， EGABEIAD，FHAB，FJAD，垂足分别为 G，I，H，J 根据对称性可知：四边形 EFHG 的面积与四边形 EFJI 的面积相等，AIE 的面积 AEG 的面积， S阴S正方形ABCD， 故选：B 10 【解答】解：作线段 BC 的垂直平分线可得线段 BC 的中点 由此可知：选项 A 符合条件， 故选：A 11 【解答】解：A、ACB 与ACD 的大小关系不确定，AB 与 AD 不一定相等，故本 选项错误； B、AC 平分BAD，BACDAC，BCCD，故本选项正确； C、ACB 与ACD 的大小关系不确定，与不一定相等，故本选
17、项错误； D、BCA 与DCA 的大小关系不确定，故本选项错误 故选：B 12 【解答】解：直线 AB 是O 的切线，C 为切点， OCB90， ODAB， COD90， CEDCOD45， 故选：D 13 【解答】解：a7，b5，c6 p9， ABC 的面积 S6； 故选：A 14 【解答】解：PAPB，PC100 米，PCA35， 小河宽 PAPCtanPCA100tan35米 故选：C 15 【解答】解：p，F0， p 随 S 的增大而减小， A，B，C 三个面的面积比是 4：2：1， p1，p2，p3的大小关系是：p3p2p1 故选：D 二解答题（共二解答题（共 9 小题）小题） 16
18、 【解答】解：原式+， 当 xy，yx+8 时， 原式x+（x+8）8 17 【解答】解： 解不等式，得：x1； 解不等式，得：x2； 原不等式组的解集是 1x2 18 【解答】解： （1）表格中 5 个数据按从小到大的顺序排列为 1200，1200，1300，1300， 1500， 所以中位数是 1300； （2）平均每天需要租用自行车却未租到车的人数： （1500+1200+1300+1300+1200）5 1300， YC 市首批一次性投放公共自行车 700 辆供市民租用出行， 平均每天需要租用公共自行车的人数是 1300+7002000 19 【解答】解： （1）若市民张先生某次在该停
19、车场停车 2 小时 10 分钟，应交停车费为：3+2 27（元） ； 若李先生也在该停车场停车， 支付停车费 11 元， 则超出时间为 （113） 24 （小时） ， 所以停车场按 5 小时计时收费 故答案为：7；5； （2）当 x 取整数且 x1 时，该停车场停车费 y（单位：元）关于停车计时 x（单位：小 时）的函数解析式为：y3+2（x1） ， 即 y2x+1 20 【解答】解： （1）这 5 个数从小到大排列：5，5，10，10，15，故中位数为 10， 故答案为 10 （2）没有选择的占 110%30%20%10%20%10%， 条形图的高度和 E 相同；如图所示： （3）14002
20、0%280（名） 答：估计全校有多少学生愿意参加环保义工社团有 280 名； （4）酵素制作社团、绿植养护社团分别用 A、B 表示：树状图如图所示， 共有 4 种可能，两人同时选择绿植养护社团只有一种情形， 这两名同学同时选择绿植养护社团的概率 21 【解答】解： （1）证明：四边形 ABCD 是平行四边形， ADBC， AHC90， HAD90，即 OAAD， 又OA 为半径， AD 是O 的切线； （2）解：如右图，连接 OC， OHOA，AH3， OH1，OA2， 在 RtOHC 中，OHC90，OHOC， OCH30， AOCOHC+OCH120， S扇形OAC， CH， SOHC1，
21、 四边形 ABCD 与O 重叠部分的面积S扇形OAC+SOHC+； （3）设O 半径 OArOC，OH3r， 在 RtOHC 中，OH2+HC2OC2， （3r）2+12r2， r，则 OH， 在 RtABH 中，AH3，BH+1，则 AB， 在 RtACH 中，AH3，CHNH1，得 AC， 在BMN 和BCA 中， BB，BMNBCA， BMNBCA， 即， MN， OH，MN 22 【解答】解： （1）三年用于辅助配套的投资将达到 5436（亿元） ； （2）设 2015 年年初，对辅助配套的投资为 x 亿元，则线路敷设的投资为 2x 亿元，搬迁 安置的投资是 4x 亿元， 根据题意，得
22、：， 解得：， 市政府 2015 年年初对三项工程的总投资是 7x35 亿元； （3）由 x5 得，2015 年初搬迁安置的投资为 20 亿元， 设从 2016 年初开始，搬迁安置投资逐年递减的百分数为 y， 由题意，得：20（1y）25， 解得：y10.5，y21.5（舍） 答：搬迁安置投资逐年递减的百分数为 50% 23 【解答】解： （1）在矩形 ABCD 中，AD90，ABDC， E 是 AD 中点， AEDE， 在ABE 和DCE 中， ABEDCE（SAS） ； （2）在矩形 ABCD，ABC90， BPC 沿 PC 折叠得到GPC， PGCPBC90，BPCGPC， BECG，
23、BEPG， GPFPFB， BPFBFP， BPBF； 当 AD25 时， BEC90， AEB+CED90， AEB+ABE90， CEDABE， AD90， ABEDEC， ， 设 AEx， DE25x， ， x9 或 x16， AEDE， AE9，DE16， CE20，BE15， 由折叠得，BPPG， BPBFPG， BEPG， ECFGCP， ， 设 BPBFPGy， ， y， BP， 在 RtPBC 中，PC，cosPCB； 如图，连接 FG， GEFPGC90， GEF+PGC180， BFPG BFPG， BPGF 是菱形， BPGF， GFEABE， GEFEAB， ， BEE
24、FABGF129108 24 【解答】解： （1）由点 A（2，4） ，B（2，2）可知正方形的边长为 6， 正方形面积为 36； 有四个交点时 0k4 或8k0； 故答案为 36，0k4 或8k0； （2）由题意可知，2m4，yQm22m+3（m+1）2+4， 当 m1，yQ最大4，在运动过程中点 Q 在最高位置时的坐标为（1，4） ， 当 m1 时，yQ随 m 的增大而增大，当 m2 时，yQ最小3， 当 m1 时，yQ随 m 的增大而减小，当 m4 时，yQ最小21， 321， yQ最小21，点 Q 在最低位置时的坐标（4，21） ， 在运动过程中点 Q 在最高位置时的坐标为 （1， 4
25、） ， 最低位置时的坐标为 （4， 21） ； 当双曲线 y经过点 B（2，2）时，k4， N（4，1） ， 顶点 P（m，n）在边 BC 上， n2， BPm+2，CP4m， 抛物线 ya（xm）22（a0）与边 AB、DC 分别交于点 E、F， E（2，a（2m）22） ，F（4，a（4m）22） ， BEa（2m）2，CFa（4m）2， a（m+2）a（4m）2am2a2a（m1） ， AENF，点 F 在点 N 下方， 6a（2m）23a（4m）2， 12a（m1）3， a（m1）， ； 由题意得，M（1，a（1m）22） ， yMa（1m）22（2m4） ， yMa（m1）22（2m4） ， a0， 对应每一个 a（a0）值，当 m1 时，yM最小2， 当 m2 或 4 时，yM最大9a2， 当 m4 时，ya（x4）22， F（4，2） ，E（2，36a2） ， 点 E 在边 AB 上，且此时不与 B 重合， 236a24， 0a， 29a2， yM， 同理 m2 时，yya（x+2）22， E（2，2） ，F（4，36a2） ， 点 F 在边 CD 上，且此时不与 C 重合， 236a24， 解得 0a， 29a2， yM， 综上所述，抛物线 L 与直线 x1 的交点 M 始终位于 x 轴下方；
