1、 1 专题专题 8：相似三角形性质和判定的应用相似三角形性质和判定的应用 【典例引领】【典例引领】 例：如图，在矩形 ABCD 中，AB=3，BC=5，E 是 AD 上的一个动点 （1）如图 1，连接 BD，O 是对角线 BD 的中点，连接 OE当 OE=DE 时，求 AE 的长； （2）如图 2，连接 BE，EC，过点 E 作 EFEC 交 AB 于点 F，连接 CF，与 BE 交于点 G当 BE 平分 ABC 时，求 BG 的长； （3）如图 3，连接 EC，点 H 在 CD 上，将矩形 ABCD 沿直线 EH 折叠，折叠后点 D 落在 EC 上的点 D处， 过点 D作 DNAD 于点 N
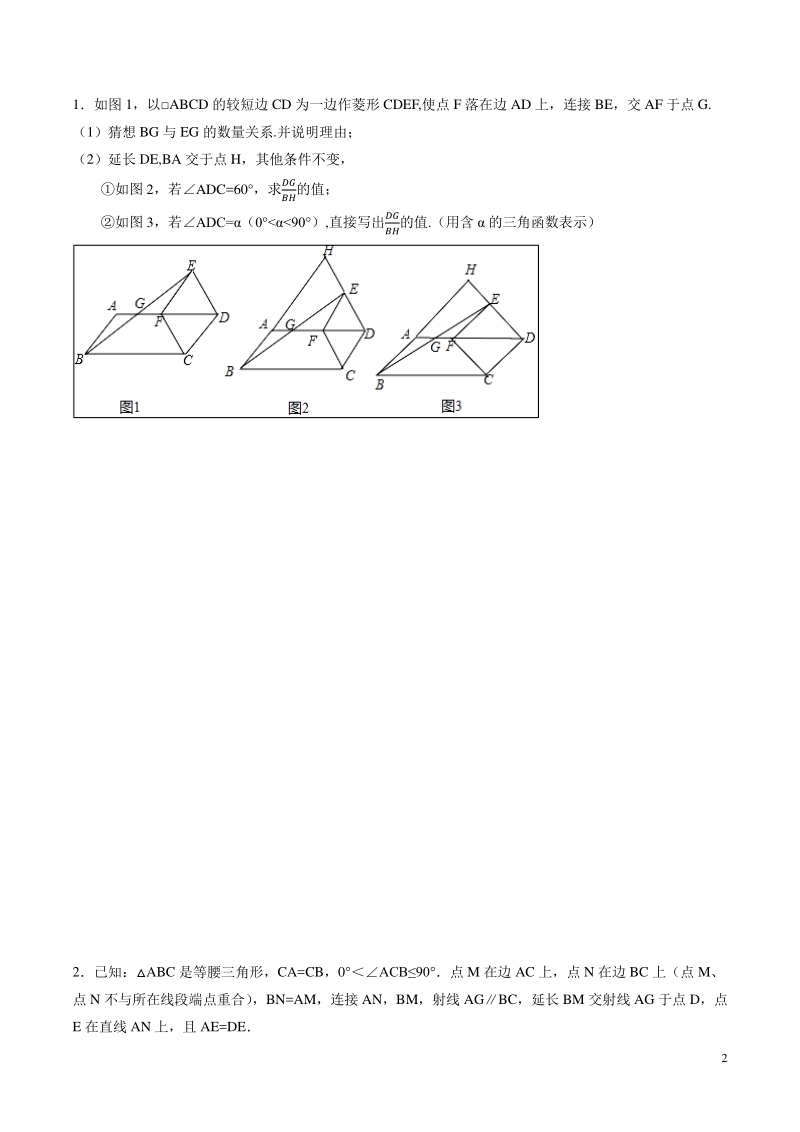
2、，与 EH 交于点 M，且 AE=1 求 的值； 连接 BE，DMH 与CBE 是否相似？请说明理由 【强化训练】【强化训练】 2 1如图 1，以ABCD 的较短边 CD 为一边作菱形 CDEF,使点 F 落在边 AD 上，连接 BE，交 AF 于点 G. （1）猜想 BG 与 EG 的数量关系.并说明理由； （2）延长 DE,BA 交于点 H，其他条件不变， 如图 2，若ADC=60 ，求 的值； 如图 3，若ADC=（090）,直接写出 的值.（用含 的三角函数表示） 2已知：ABC 是等腰三角形，CA=CB，0 ACB90点 M 在边 AC 上，点 N 在边 BC 上（点 M、 点 N
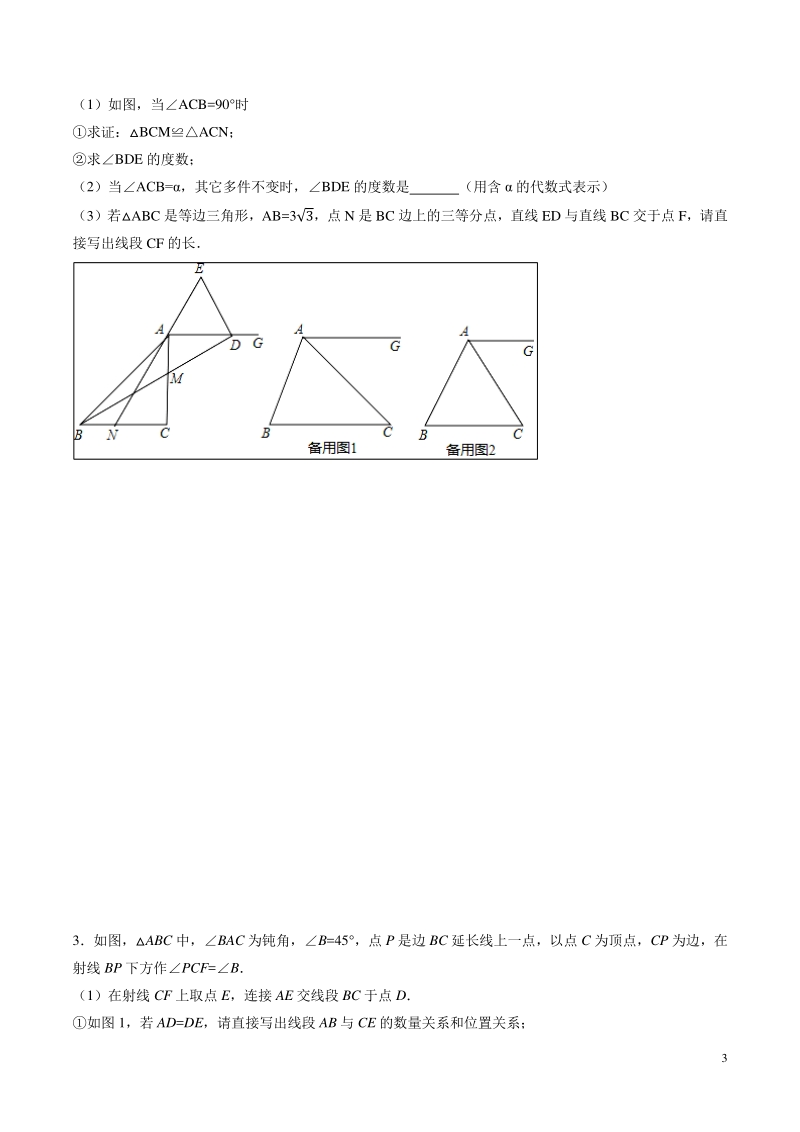
3、不与所在线段端点重合） ，BN=AM，连接 AN，BM，射线 AGBC，延长 BM 交射线 AG 于点 D，点 E 在直线 AN 上，且 AE=DE 3 （1）如图，当ACB=90 时 求证：BCMACN； 求BDE 的度数； （2）当ACB=，其它多件不变时，BDE 的度数是 （用含 的代数式表示） （3）若ABC 是等边三角形，AB=33，点 N 是 BC 边上的三等分点，直线 ED 与直线 BC 交于点 F，请直 接写出线段 CF 的长 3如图，ABC 中，BAC 为钝角，B=45 ，点 P 是边 BC 延长线上一点，以点 C 为顶点，CP 为边，在 射线 BP 下方作PCF=B （1）
4、在射线 CF 上取点 E，连接 AE 交线段 BC 于点 D 如图 1，若 AD=DE，请直接写出线段 AB 与 CE 的数量关系和位置关系； 4 如图 2，若 AD=2DE，判断线段 AB 与 CE 的数量关系和位置关系，并说明理由； （2）如图 3，反向延长射线 CF，交射线 BA 于点 C，将PCF 沿 CC方向平移，使顶点 C 落在点 C处，记 平移后的PCF 为PCF，将PCF绕点 C顺时针旋转角 （0 45 ） ，CF交线段 BC 于点 M，CP 交射线 BP 于点 N，请直接写出线段 BM，MN 与 CN 之间的数量关系 4 （2016 辽宁省大连市）阅读下面材料： 小明遇到这样
5、一个问题：如图 1，ABC 中，AB=AC，点 D 在 BC 边上，DAB=ABD，BEAD，垂足为 E，求证：BC=2AE 小明经探究发现，过点 A 作 AFBC，垂足为 F，得到AFB=BEA，从而可证ABFBAE（如图 2） ， 使问题得到解决 （1）根据阅读材料回答：ABF 与BAE 全等的条件是 AAS（填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的 5 一个） 参考小明思考问题的方法，解答下列问题： （2）如图 3，ABC 中，AB=AC，BAC=90 ，D 为 BC 的中点，E 为 DC 的中点，点 F 在 AC 的延长线上， 且CDF=EAC，若 CF=2，求
6、AB 的长； （3）如图 4，ABC 中，AB=AC，BAC=120 ，点 D、E 分别在 AB、AC 边上，且 AD=kDB（其中 0k 3 3 ） ，AED=BCD，求 的值（用含 k 的式子表示） 5我们把两条中线互相垂直的三角形称为“中垂三角形”例如图 1，图 2，图 3 中，AF，BE 是ABC 的中 线，AFBE，垂足为 P，像ABC 这样的三角形均为“中垂三角形”设 BCa，ACb，ABc 特例探索 （1）如图 1，当ABE45 ，c22时，a ，b ； 如图 2，当ABE30 ，c4 时，a ，b ； 6 归纳证明 （2）请你观察（1）中的计算结果，猜想 a2，b2，c2三者之间的关系，用等式表示出来，请利用图 3 证明你 发现的关系式； 拓展应用 （3）如图 4，在ABCD 中，点 E，F，G 分别是 AD，BC，CD 的中点，BEEG，AD25，AB3求 AF 的长
