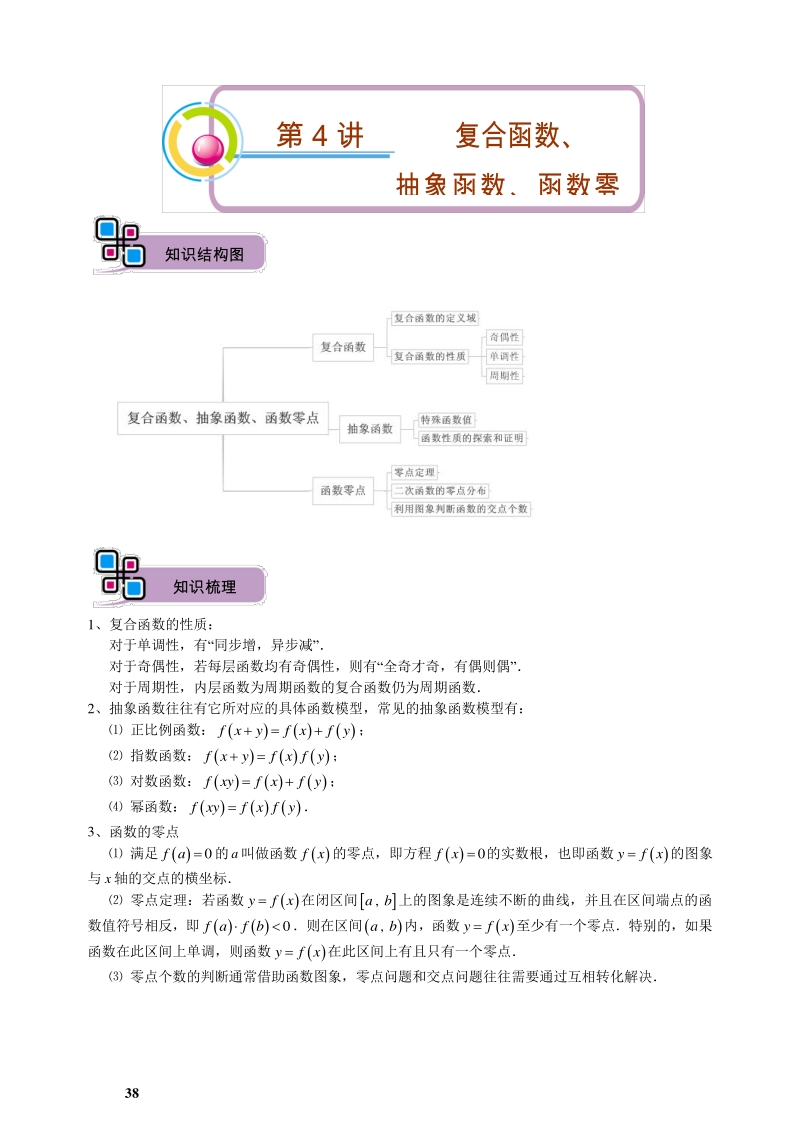
1、 38 1、复合函数的性质： 对于单调性，有“同步增，异步减” 对于奇偶性，若每层函数均有奇偶性，则有“全奇才奇，有偶则偶” 对于周期性，内层函数为周期函数的复合函数仍为周期函数 2、抽象函数往往有它所对应的具体函数模型，常见的抽象函数模型有： 正比例函数： f xyf xf y； 指数函数： f xyf x f y； 对数函数： f xyf xf y； 幂函数： f xyf x f y 3、函数的零点 满足 0f a 的a叫做函数 f x的零点，即方程 0f x 的实数根，也即函数 yf x的图象 与x轴的交点的横坐标 零点定理：若函数 yf x在闭区间,ab上的图象是连续不断的曲线，并且在
2、区间端点的函 数值符号相反，即 0f af b则在区间,a b内，函数 yf x至少有一个零点特别的，如果 函数在此区间上单调，则函数 yf x在此区间上有且只有一个零点 零点个数的判断通常借助函数图象，零点问题和交点问题往往需要通过互相转化解决 知识梳理 知识结构图 第 4 讲 复合函数、 抽象函数、函数零 39 1、 （2007 北京理）对于函数 lg21f xx， 2 2f xx， cos2f xx， 判断如下三个命题的真假： 命题甲：2f x是偶函数； 命题乙： f x在, 2上是减函数，在2, 上是增函数； 命题丙： 2f xf x在, 上是增函数 能使命题甲、乙、丙均为真的所有函数
3、的序号是 A B C D 【解析】 D 2、 （2011 北京理 13）已知函数 3 2 2 12 x x f x xx ， ， ，若关于x的方程 f xk有两个不同的 实根，则实数k的取值范围是 【解析】 0, 1； 1、 2 1 3 log54yxx的单调递增区间为（ ） A, 1 B 5 , 2 C 5 , 4 2 D4, 2、 设函数 x f xa（0a 且1a ） ， 24f，则（ ） A21ff B12ff C 12ff D 22ff 3、 已知 log2 a f xax是0, 1上的减函数，则a的值可能为（ ） A 1 2 B 3 2 C2 D3 4、 已知函数 2xf xx，
4、2 logg xxx， 2 log2h xx的零点分别为a、b、c，则 （ ） Aabc Bacb Cbac Dcab 5、 已知函数 2f xxaxb（ab） ， 并且、是方程 0f x 的两个根 （） ， 则实数a、b、的大小关系是（ ） Aab Bab Cab Dab 6、 已知函数 2 2f xxxc， 1 fxf x， 1nn fxffx （2n，n N） ，若函 数 n fxx不存在零点，则c的取值范围是（ ） A 1 4 c B 3 4 c C 9 4 c D 9 4 c 7、 下列关于函数 log1 x a f xa（0a 且1a ）的命题： 小题热身 真题再现 40 无论a取
5、何值， f x均为R上的增函数； 无论a取何值， f x的值域均为R； 无论a取何值， f x一定有零点； 存在某个a，使得 f x恰好有两个零点 其中正确的命题个数为（ ） A0 B1 C2 D3 8、 若单调函数 f x（xR）满足 f xyf xf y，则 f x的值域为（ ） AR B, 00, C0, D不能确定 9、 已知函数 2 243f xxx ， 设 F xp f f xf x ， 其中p为负实数 若 F x 在区间,3上是减函数，在区间3, 0上是增函数，则p的值为（ ） A1 B 1 8 C 1 16 D 1 2 10、 已知函数 2 f xaxbxc（0a ） ，则关于
6、x的方程 2 0m f xnf xp （实数 ,0abcmnp）的解集不可能是（ ） A1, 2 B1, 4 C1, 2, 3, 4 D1, 4, 16, 64 1 2 3 4 5 6 7 8 9 10 A A B A A C C C C D 考点：复合函数的定义域与值域 【例1】 函数 1 2 x f x 的定义域为 ，值域为 函数 2 1 1 ( ) 2 x f x 的定义域为 ，值域为 函数 2 11 22 loglog2yxx 的定义域为_，值域为_ 【解析】 0, ，0, 1； 1 1 ， 1 , 1 2 ； 1 04 2 ，0)，； 【例2】 已知函数 2 lg21f xaxx的定
7、义域为R，求实数a的取值范围 已知函数 2 lg21f xaxx的值域为R，求实数a的取值范围 4.1 复合函数 经典精讲 41 【解析】 1, ； 0,1； 【拓1】 已知 3 2logf xx，1, 9x，求函数 2 2 yf xf x 的值域 设 2 ,1 ( ) ,1 xx f x xx ，( )g x是二次函数，若 fg x 的值域是 0, ，求函数( )g x的值 域 设2, 8x，函数 2 1 ( )loglog 2 aa f xaxa x的最大值是 1，最小值是 1 8 ，求a的值 【解析】 6 ,13 0, 1 2 a 考点：复合函数的性质初步 【例3】 函数 2 1 2 l
8、og56yxx的单调增区间为（ ） A 5 2 ， B(3)， C 5 2 ， D(2)， 函数 2 2 1 2 xx y 的单调递增区间是（ ） A 1 1, 2 B,1 C2, D 1 , 2 2 函数421 xx y 的值域为_，单调递减区间为_ 【解析】 D； D； 3 , 4 ；,1 考点：复合函数的性质综合 【例4】 函数 2 1 2 log23fxxax，若 f x在, 1内是增函数，则a的取值范围为 _； 若 f x的单调递增区间是, 1，则a的取值范围为_ 已知函数 3 1 1 ax f xa a ，若 f x在区间0,1上是减函数，则实数a的取值范 围是 若函数 2 log
9、2 a f xxx（0a 且1a ）在区间 1 0, 2 内恒有 0f x ，则 f x的 单调增区间是 【解析】 1 2)，；1 , 01, 3； 42 1 , 2 考点：抽象函数的函数值问题 【例5】 若奇函数 f x（xR）满足 21f， 22f xf xf，则 1f ； 定义在实数R上的函数 yf x具有如下性质： 对任意xR，都有 3 3 f xf x ； 对任意 12 xx R，且 12 xx，都有 12 f xf x 则 101fff_ 已知函数 f x（xR）满足 12f， 2f xyf xf yxy，则 2f ， 3f ，3f f x是定义在(0)，上的增函数， 对正实数x、
10、y都有 f xyf xf y成立 则 不等式 2 log0fx 的解集为_ _ 【解析】 1 2 ； 0； 6，12，6； 1, 2； 【拓2】 定义在0, 1上函数 f x满足： 00f； 11f xfx； 1 32 x ff x ； 对任意 12 ,xx0, 1，若 12 xx，则 12 f xf x 则 1f ， 1 2 f ， 1 3 f ， 1 8 f 【追问】 1 2013 f 【解析】 11f； 11 22 f ； 11 32 f ； 11 84 f 【追问】 11 2013128 f 考点：抽象函数的性质 4.2 抽象函数 43 【例6】 若函数 f x（xR， 且0x ） 对
11、任意的非零实数,xy满足 f xyf xf y 求证： f x为偶函数 定义在R上的函数 f x同时满足下列条件： 对任意x，yR，恒有 f xyf xf y； 当0x 时， 0f x ，且 12f 判断函数 f x的奇偶性，并求函数( )f x在区间2, 4上的最大值和最小值 【解析】 令1,1xy 得( 1)(1)( 1)fff， 于是(1)0f； 再令1xy 得(1)2 ( 1)0ff， 于是( 1)0f 令1y 得()( )( 1)( )fxf xff x，又( )f x的定义域关于原点对称故( )f x为偶函数 ( )f x在区间2, 4上的最大值是( 2)4f ，最小值为(4)8f
12、 【备注】本题可以通过函数原型快速得到答案或得到启发 对于( )lnf xx（xR）是符合函数的函数原型； 对于 2f xx （xR）是符合函数的函数原型 【拓3】 函数( )f x的定义域为R，且( )f x的值不恒为0，又对于任意的实数m，n，总有 ( ) ( ) 22 nm f m f nmfnf 成立 求(0)f的值； 求证：( )0t f t对任意的tR成立； 求所有满足条件的函数( )f x 【解析】 (0)0f； 对任意tR，令2mnt，得 2(2 ) 4( )ftt f t，于是 2 1 ( )(2 )0 4 t f tft； ( )f xx 考点：零点定理 【例7】 函数(
13、)237 x f xx在区间02，上的零点必在下面的区间（ ）内 1 0 2 ， 1 1 2 ， 3 1 2 ， 3 2 2 ， 设函数 3 2 log x f xa x 在区间1, 2内有零点，则实数a的取值范围是（ ） A 3 1,log 2 B 3 0, log 2 C 3 log 2 ,1 D 3 1, log 4 【解析】 C； C； 考点：函数图象与零点、交点问题 【例8】 方程 2 log (3)2xx的解的情况是（ ） A仅有一根 B有两个正根 4.3 函数零点 44 C有一个正根和一个负根 D有两个负根 已知 2 881 651 xx f x xxx ， ， ， lng xx
14、，则 f x与 g x的图象的交点个数为 （ ） A1 B2 C3 D4 若函数( ) x f xaxa（0a 且1a ）有两个零点，则实数a的取值范围是 若不等式 2 log0 a xx对 1 0 2 x ，恒成立，则实数a的取值范围是_ 【解析】 C； C； (1,)； 1 1 16 ，； 考点：复合函数的零点问题 【例9】 已知函数 yf x和 yg x在2, 2的图象如下所示： -2 2 -2 2 y -1 1 -11O x -2 2 -2 2 y -1 1 -11O x f x g x 给出下列四个命题： 方程 0fg x 有且仅有6个根 方程 0gf x 有且仅有3个根 方程 0f
15、f x 有且仅有5个根 方程 0g g x 有且仅有4个根 其中正确的命题是 （将所有正确的命题序号填在横线上） 设 1 ,1 1( ) 1,1 x xf x x ，若关于x的方程 2 0fxbfxc 有三个不同的实数解 123 ,xxx，则 222 123 xxx等于 【解析】 ； 5； 【拓4】 已知 2 f xxpxq，关于x的方程 0ff x有且只有一个实数根，求证：p与q同时 大于0或者p与q同时等于0 【解析】 关于x的方程 0ff x有且只有一个实数根， f x的图象只有如图两种情形（分别对应 0 和0 的情形）进而容易证明命题成立 45 y=x2 y=x1 x2x1 y O x
16、 Ox y 一、选择题 1、 设 2 31 32 xx f xk，当0x 时 f x恒取正值，则k的取值范围为（ ） A,1 B , 2 21 C 1, 2 21 D 2 21, 2 21 【解析】 B； 2、 设函数 3 yx与 2 1 2 x y 的图象的交点为 00 ()xy，则 0 x所在的区间是（ ） A(01)， B(12)， C(23)， D(34)， 【解析】 B； 3、 关于x的方程 1 log(0 x a ax a且1)a （ ） A仅当1a 时，有唯一解 B仅当01a时，有唯一解 C有唯一解 D无解 【解析】 C 4、 设函数( )f xx xbxc，给出下列四个命题：
17、当0c 时，( )yf x是奇函数； 当00bc，时，方程( )0f x 只有一个实根； 函数( )yf x的图象关于点(0) c，对称； 方程( )0f x 至多有两个实根； 其中正确命题的个数为（ ） A1 个 B2 个 C3 个 D4 个 【解析】 C； 二、填空题 5、 设函数 22 ( )loglog (1)f xxx，则( )f x的定义域是_；( )f x的最大值是_ 【解析】 (0 ,1)；2 6、 函数 22 ( )log (3)log (1)f xxx的值域是_，单调递增区间为_ 【解析】 (, 2，( 3,1) 课后习题 46 7、 若log (2) a yax在01，上
18、是x的减函数，则a的取值范围是_ 【解析】 (12)a，； 三、解答题 8、 已知定义域为R的函数 f x满足： f xyf x f y，且 31f 求 0f；求证：41f 【解析】 (0)1f； 3 (3)(2) (1)(1)1ffff，故(1)1f，从而 24 (4)(2)(1)1fff 令4 ,4xy 得，(4) ( 4)(0)1fff，故 1 ( 4)1 (4) f f 命题得证 【备注】 f xyf x f y的函数原型是指数函数( ) x f xa，由(3)1f知，1a 9、 函数 2xf x 和 3 g xx的图象的示意图如图所示设两函数的图象交于点 11 ,A xy、 22 ,
19、B xy，且 12 xx x1x2 B A C2 C1 y Ox 请指出示意图中曲线 1 C、 2 C分别对应哪一个函数？ 若 1 ,1xaa， 2 ,1xb b，且,1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12a b，指出 a、b的值，并说明理由； 结合函数图象示意图，请把 f、 g、2013f、2013g四个数从小到大顺序排列 【解析】 1 C对应函数 3 g xx， 2 C对应函数 2xf x ； 如下表，可得1a ，9b 1 2 3 4 5 6 7 8 9 10 11 12 f x 2 4 8 16 32 64 128 256 512 1024 2048 4096 g x 1 8 27 64 125 216 343 512 729 1000 1331 1728 20132013fggf 10、 已知关于x的二次方程 2 2210xmxm 若方程有两根，其中一根在区间1, 0内，另一根在区间1, 2内，求m的范围 若方程两根均在区间0, 1内，求m的范围 【解析】 51 62 m 1 12 2 m
