2020年3月安徽省中考数学模拟训练试卷（含答案解析）

《2020年3月安徽省中考数学模拟训练试卷（含答案解析）》由会员分享，可在线阅读，更多相关《2020年3月安徽省中考数学模拟训练试卷（含答案解析）（25页珍藏版）》请在七七文库上搜索。

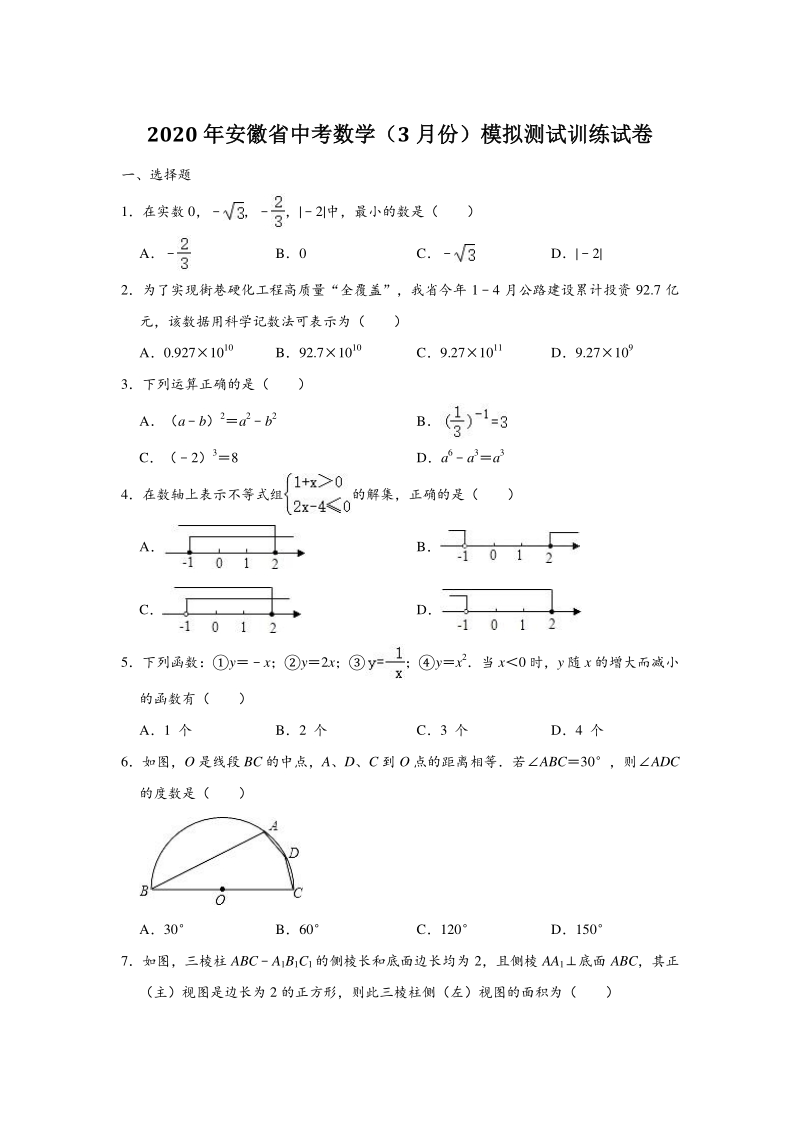
1、2020 年安徽省中考数学（年安徽省中考数学（3 月份）模拟测试训练试卷月份）模拟测试训练试卷 一、选择题 1在实数 0，|2|中，最小的数是（ ） A B0 C D|2| 2为了实现街巷硬化工程高质量“全覆盖”，我省今年 14 月公路建设累计投资 92.7 亿 元，该数据用科学记数法可表示为（ ） A0.9271010 B92.71010 C9.271011 D9.27109 3下列运算正确的是（ ） A（ab）2a2b2 B C（2）38 Da6a3a3 4在数轴上表示不等式组的解集，正确的是（ ） A B C D 5下列函数：yx；y2x；yx2当 x0 时，y 随 x 的增大而减小 的

2、函数有（ ） A1 个 B2 个 C3 个 D4 个 6如图，O 是线段 BC 的中点，A、D、C 到 O 点的距离相等若ABC30，则ADC 的度数是（ ） A30 B60 C120 D150 7如图，三棱柱 ABCA1B1C1的侧棱长和底面边长均为 2，且侧棱 AA1底面 ABC，其正 （主）视图是边长为 2 的正方形，则此三棱柱侧（左）视图的面积为（ ） A B C D4 8古希腊著名的毕达哥拉斯学派把 1，3，6，10这样的数称为“三角形数”，而把 1，4， 9，16这样的数称为“正方形数”从图中可以发现，任何一个大于 1 的“正方形数” 都可以看作两个相邻“三角形数”之和下列等式中，

3、符合这一规律的是（ ） A133+10 B259+16 C3615+21 D4918+31 9某市 2012 年国内生产总值（GDP）比 2011 年增长了 12%，由于受到国际金融危机的影 响，预计 2013 年比 2012 年增长 7%若这两年 GDP 平均增长率为 x%，则 x%满足的关 系是（ ） A12%+7%x% B（1+12%）（1+7%）2（1+x%） C12%+7%2 x% D（1+12%）（1+7%）（1+x%）2 10二次函数 yax2+bx+1（a0）的图象的顶点在第一象限，且过点（1，0）设 t a+b+1，则 t 值的变化范围是（ ） A0t1 B0t2 C1t2

4、D1t1 二、填空题（共 4 小题） 11因式分解：9a3bab 12甲、乙两名射击运动员在一次训练中，每人各打 10 发子弹，根据命中环数求得方差分 别是0.6，0.8，则运动员 的成绩比较稳定 13在平面直角坐标系中，P 的圆心是（2，a）（a2），半径为 2，函数 yx 的图象被 P 截得的弦 AB 的长为，则 a 的值是 14如图，在ABC 中，ABC 和ACB 的平分线相交于点 O，过点 O 作 EFBC 交 AB 于 E， 交 AC 于F， 过点O 作ODAC于 D 下列四个结论： BOC90+A； EF BE+CF；设 ODm，AE+AFn，则 SAEFmn； EF 是ABC 的

5、中位线其 中正确的结论是 三、（共 2 小题，每小题 8 分，满分 16 分） 15先化简，再求值：（1），其中 a+1 16小强在教学楼的点 P 处观察对面的办公大楼为了测量点 P 到对面办公大楼上部 AD 的距离， 小强测得办公大楼顶部点A的仰角为45， 测得办公大楼底部点B的俯角为60， 已知办公大楼高 46 米，CD10 米求点 P 到 AD 的距离（用含根号的式子表示） 四、（共 2 小题，每小题 8 分，满分 16 分） 17如图所示，正方形网格中，ABC 为格点三角形（即三角形的顶点都在格点上） （1） 把ABC 沿 BA 方向平移后， 点 A 移到点 A1， 在网格中画出平移后

6、得到的A1B1C1； （2）把A1B1C1绕点 A1按逆时针方向旋转 90，在网格中画出旋转后的A1B2C2； （3）如果网格中小正方形的边长为 1，求点 B 经过（1）、（2）变换的路径总长 18为实施“农村留守儿童关爱计划”，某校对全校各班留守儿童的人数情况进行了统计， 发现各班留守儿童人数只有 1 名、2 名、3 名、4 名、5 名、6 名共六种情况，并制成如下 两幅不完整的统计图： （1）求该校平均每班有多少名留守儿童？并将该条形统计图补充完整； （2）某爱心人士决定从只有 2 名留守儿童的这些班级中，任选两名进行生活资助，请用 列表法或画树状图的方法，求出所选两名留守儿童来自同一个班

7、级的概率 五、（共 2 小题，每小题 10 分，满分 20 分） 19已知一次函数 y1x+m 的图象与反比例函数 y2的图象交于 A、B 两点已知当 x1 时，y1y2；当 0x1 时，y1y2 （1）求一次函数的解析式； （2）已知双曲线在第一象限上有一点 C 到 y 轴的距离为 3，求ABC 的面积 20已知：如图，在平行四边形 ABCD 中，点 M 在边 AD 上，且 AMDMCM、BA 的延 长线相交于点 E求证： （1）AEAB； （2）如果 BM 平分ABC，求证：BMCE 六、（本题满分 12 分） 21（1）解下列方程：根为 ；根为 ；根 为 ； （2）根据这类方程特征，写出

8、第 n 个方程为 ，其根为 （3）请利用（2）的结论，求关于 x 的方程（n 为正整数）的根 七、（本题满分 12 分） 22为了扶持大学生自主创业，市政府提供了 80 万元无息贷款，用于某大学生开办公司生 产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款已 知该产品的生产成本为每件 40 元，员工每人每月的工资为 2500 元，公司每月需支付其 它费用 15 万元该产品每月销售量 y（万件）与销售单价 x（元）之间的函数关系如图 所示 （1）求月销售量 y（万件）与销售单价 x（元）之间的函数关系式； （2）当销售单价定为 50 元时，为保证公司月利润达到 5 万元（

9、利润销售额生产成 本员工工资其它费用），该公司可安排员工多少人？ （3）若该公司有 80 名员工，则该公司最早可在几个月后还清无息贷款？ 八、（本题满分 14 分） 23 在锐角ABC 中， AB4， BC5， ACB45， 将ABC 绕点 B 按逆时针方向旋转， 得到A1BC1 （1）如图 1，当点 C1在线段 CA 的延长线上时，求CC1A1的度数； （2）如图 2，连接 AA1，CC1若ABA1的面积为 4，求CBC1的面积； （3）如图 3，点 E 为线段 AB 中点，点 P 是线段 AC 上的动点，在ABC 绕点 B 按逆时 针方向旋转过程中，点 P 的对应点是点 P1，求线段 EP

10、1长度的最大值与最小值 参考答案 一、选择题（共 10 小题，每小题 4 分，满分 40 分） 1在实数 0，|2|中，最小的数是（ ） A B0 C D|2| 【分析】根据正数大于负数和 0，0 大于负数，两个负数绝对值大的反而小，即可解答 解：|，|2|2， ， ， 最小的数是， 故选：C 2为了实现街巷硬化工程高质量“全覆盖”，我省今年 14 月公路建设累计投资 92.7 亿 元，该数据用科学记数法可表示为（ ） A0.9271010 B92.71010 C9.271011 D9.27109 【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，

11、要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相 同当原数绝对值1 时，n 是正数；当原数的绝对值1 时，n 是负数 解：将 92.7 亿亿元用科学记数法表示为 9.27109元 故选：D 3下列运算正确的是（ ） A（ab）2a2b2 B C（2）38 Da6a3a3 【分析】根据完全平方公式以及负指数次幂和乘方的性质，以及同类项的定义即可进行 判断 解：A、（ab）2a22ab+b2，故选项错误； B、正确； C、（2）38，故选项错误； D、a6和a3不是同类项，不能合并，选项错误 故选：B 4在数轴上表示不等式组的解集，正确的是（ ） A B C D 【分析

12、】先解不等式组中的每一个不等式，再把不等式的解集表示在数轴上，即可 解：解不等式组得 分别表示在数轴上为： 故选：C 5下列函数：yx；y2x；yx2当 x0 时，y 随 x 的增大而减小 的函数有（ ） A1 个 B2 个 C3 个 D4 个 【分析】分别根据一次函数、反比例函数及二次函数的性质进行逐一判断即可 解：一次函数 yx 中 k0，y 随 x 的增大而减小，故本小题正确； 正比例函数 y2x 中， k2， 0， 当 x0 时， y 随 x 的增大而增大， 故本小题错误； 反比例函数中 k10，当 x0 时函数的图象在第二象限，此时 y 随 x 的增大而增大，故本小题错误； 二次函数

13、 yx2，中 a10，此抛物线开口向上，当 x0 时，y 随 x 的增大而减 小，故本选项正确 故选：B 6如图，O 是线段 BC 的中点，A、D、C 到 O 点的距离相等若ABC30，则ADC 的度数是（ ） A30 B60 C120 D150 【分析】根据圆内接四边形的性质即可求出ADC 的度数 解：四边形 ABCD 内接于O， ADC+ABC180，即ADC150 故选：D 7如图，三棱柱 ABCA1B1C1的侧棱长和底面边长均为 2，且侧棱 AA1底面 ABC，其正 （主）视图是边长为 2 的正方形，则此三棱柱侧（左）视图的面积为（ ） A B C D4 【分析】易得等边三角形的高，那

14、么左视图的面积等边三角形的高侧棱长，把相关 数值代入即可求解 解：易得三棱柱的底面为等边三角形，边长为 2，作出等边三角形的高后，组成直角三角 形，底边的一半为 1， 等边三角形的高为， 侧（左）视图的面积为 22， 故选：B 8古希腊著名的毕达哥拉斯学派把 1，3，6，10这样的数称为“三角形数”，而把 1，4， 9，16这样的数称为“正方形数”从图中可以发现，任何一个大于 1 的“正方形数” 都可以看作两个相邻“三角形数”之和下列等式中，符合这一规律的是（ ） A133+10 B259+16 C3615+21 D4918+31 【分析】本题考查探究、归纳的数学思想方法题中明确指出：任何一个

15、大于 1 的“正 方形数”都可以看作两个相邻“三角形数”之和由于“正方形数”为两个“三角形数” 之和，正方形数可以用代数式表示为：（n+1）2，两个三角形数分别表示为n（n+1） 和（n+1）（n+2），所以由正方形数可以推得 n 的值，然后求得三角形数的值 解：显然选项 A 中 13 不是“正方形数”；选项 B、D 中等式右侧并不是两个相邻“三角 形数”之和 故选：C 9某市 2012 年国内生产总值（GDP）比 2011 年增长了 12%，由于受到国际金融危机的影 响，预计 2013 年比 2012 年增长 7%若这两年 GDP 平均增长率为 x%，则 x%满足的关 系是（ ） A12%+

16、7%x% B（1+12%）（1+7%）2（1+x%） C12%+7%2 x% D（1+12%）（1+7%）（1+x%）2 【分析】根据增长率为 12%，7%，可表示出 2012 年的国内生产总值，2013 年的国内生 产总值； 求 2 年的增长率， 可用 2011 年的国内生产总值表示出 2013 年的国内生产总值， 让 2013 年的国内生产总值相等即可求得所列方程 解：设 2011 年的国内生产总值为 1， 2012 年国内生产总值（GDP）比 2011 年增长了 12%， 2012 年的国内生产总值为 1+12%； 2013 年比 2012 年增长 7%， 2013 年的国内生产总值为（

17、1+12%）（1+7%）， 这两年 GDP 年平均增长率为 x%， 2013 年的国内生产总值也可表示为：（1+x%）2， 可列方程为：（1+12%）（1+7%）（1+x%）2 故选：D 10二次函数 yax2+bx+1（a0）的图象的顶点在第一象限，且过点（1，0）设 t a+b+1，则 t 值的变化范围是（ ） A0t1 B0t2 C1t2 D1t1 【分析】由二次函数的解析式可知，当 x1 时，所对应的函数值 yta+b+1把点（ 1，0）代入 yax2+bx+1，ab+10，然后根据顶点在第一象限，可以画出草图并判断 出 a 与 b 的符号，进而求出 ta+b+1 的变化范围 解：二次

18、函数 yax2+bx+1 的顶点在第一象限， 且经过点（1，0）， 易得：ab+10，a0，b0， 由 ab10 得到 b1，结合上面 b0，所以 0b1， 由 ba+10 得到 a1，结合上面 a0，所以1a0， 由+得：1a+b1， 在不等式两边同时加 1 得 0a+b+12， a+b+1t 代入得 0t2， 0t2 故选：B 二、填空题（共 4 小题，每小题 5 分，满分 20 分） 11因式分解：9a3bab ab（3a+1）（3a1） 【分析】原式提取公因式后，利用平方差公式分解即可 解：原式ab（9a21）ab（3a+1）（3a1） 故答案为：ab（3a+1）（3a1） 12甲、乙

19、两名射击运动员在一次训练中，每人各打 10 发子弹，根据命中环数求得方差分 别是0.6，0.8，则运动员 甲 的成绩比较稳定 【分析】根据方差的意义可作出判断方差是用来衡量一组数据波动大小的量，方差越 小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定， 即可求出答案 解：0.6，0.8， ， 甲的方差小于乙的方差， 甲的成绩比较稳定 故答案为：甲 13在平面直角坐标系中，P 的圆心是（2，a）（a2），半径为 2，函数 yx 的图象被 P 截得的弦 AB 的长为，则 a 的值是 【分析】过 P 点作 PEAB 于 E，过 P 点作 PCx 轴于 C，交 AB 于 D，

20、连接 PA分别 求出 PD、DC，相加即可 解：过 P 点作 PEAB 于 E，过 P 点作 PCx 轴于 C，交 AB 于 D，连接 PA AB2， AE，PA2， PE1 点 D 在直线 yx 上， AOC45， DCO90， ODC45， PDEODC45， DPEPDE45， DEPE1， PD P 的圆心是（2，a）， 点 D 的横坐标为 2， OC2， DCOC2， aPD+DC2+ 故答案为：2+ 14如图，在ABC 中，ABC 和ACB 的平分线相交于点 O，过点 O 作 EFBC 交 AB 于 E， 交 AC 于F， 过点O 作ODAC于 D 下列四个结论： BOC90+A；

21、 EF BE+CF；设 ODm，AE+AFn，则 SAEFmn； EF 是ABC 的中位线其 中正确的结论是 【分析】由在ABC 中，ABC 和ACB 的平分线相交于点 O，根据角平分线的定义与 三角形内角和定理，即可求得BOC90+A 正确；由平行线的性质和角平分线 的定义得出BEO 和CFO 是等腰三角形得出 EFBE+CF 故正确；由角平分线定理 与三角形面积的求解方法，即可求得设 ODm，AE+AFn，则 SAEFmn 正确； 因为得不出 BEAE，CFAF，所以 EF 不是ABC 的中位线 解：在ABC 中，ABC 和ACB 的平分线相交于点 O， OBCABC，OCBACB，A+A

22、BC+ACB180， OBC+OCB90A， BOC180（OBC+OCB）90+A；故正确； 在ABC 中，ABC 和ACB 的平分线相交于点 O， OBCOBE，OCBOCF， EFBC， OBCEOB，OCBFOC， EOBOBE，FOCOCF， BEOE，CFOF， EFOE+OFBE+CF， 故正确； 过点 O 作 OMAB 于 M，作 ONBC 于 N，连接 OA， 在ABC 中，ABC 和ACB 的平分线相交于点 O， ONODOMm， SAEFSAOE+SAOF AE OM+AF ODOD （AE+AF）mn；故正确； 因为已知中没有说明 AEBE，AFCF， 所以得不出 EF

23、 是ABC 的中位线， 故错误 故答案为： 三、（共 2 小题，每小题 8 分，满分 16 分） 15先化简，再求值：（1），其中 a+1 【分析】先算括号内的减法，把除法变成乘法，求出结果，最后代入求出即可 解：原式 ， 当 a+1 时，原式 16小强在教学楼的点 P 处观察对面的办公大楼为了测量点 P 到对面办公大楼上部 AD 的距离， 小强测得办公大楼顶部点A的仰角为45， 测得办公大楼底部点B的俯角为60， 已知办公大楼高 46 米，CD10 米求点 P 到 AD 的距离（用含根号的式子表示） 【分析】连接 PA、PB，过点 P 作 PMAD 于点 M；延长 BC，交 PM 于点 N，

24、将实际问 题中的已知量转化为直角三角形中的有关量， 设 PMx 米， 在 RtPMA 中， 表示出 AM， 在 RtPNB 中，表示出 BN，由 AM+BN46 米列出方程求解即可 解：连接 PA、PB，过点 P 作 PMAD 于点 M；延长 BC，交 PM 于点 N 则APM45，BPM60，NM10 米 设 PMx 米 在 RtPMA 中，AMPMtanAPMxtan45x（米） 在 RtPNB 中，BNPNtanBPM（x10）tan60（x10）（米） 由 AM+BN46 米，得 x+（x10）46 解得，188， 点 P 到 AD 的距离为米 四、（共 2 小题，每小题 8 分，满分

25、 16 分） 17如图所示，正方形网格中，ABC 为格点三角形（即三角形的顶点都在格点上） （1） 把ABC 沿 BA 方向平移后， 点 A 移到点 A1， 在网格中画出平移后得到的A1B1C1； （2）把A1B1C1绕点 A1按逆时针方向旋转 90，在网格中画出旋转后的A1B2C2； （3）如果网格中小正方形的边长为 1，求点 B 经过（1）、（2）变换的路径总长 【分析】（1）利用平移的性质画图，即对应点都移动相同的距离； （2）利用旋转的性质画图，对应点都旋转相同的角度； （3）利用弧长公式求点 B 经过（1）、（2）变换的路径总长 解：（1）连接 AA1，然后从 C 点作 AA1的平行

26、线且 AA1CC1 同理找到点 B （2）画图如下： （3）B 经过（1）、（2）变换的路径如图红色部分所示： ， 弧 B1B2的长 ， 故点 B 所走的路径总长 18为实施“农村留守儿童关爱计划”，某校对全校各班留守儿童的人数情况进行了统计， 发现各班留守儿童人数只有 1 名、2 名、3 名、4 名、5 名、6 名共六种情况，并制成如下 两幅不完整的统计图： （1）求该校平均每班有多少名留守儿童？并将该条形统计图补充完整； （2）某爱心人士决定从只有 2 名留守儿童的这些班级中，任选两名进行生活资助，请用 列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率 【分析】（1）根据留

27、守儿童有 6 名的班级有 4 个，占 20%，可求得有留守儿童的班级总 数，再求得留守儿童是 2 名的班数； （2）由（1）得只有 2 名留守儿童的班级有 2 个，共 4 名学生设 A1，A2来自一个班， B1，B2来自一个班，列出树状图可得出来自一个班的共有 4 种情况，则所选两名留守儿 童来自同一个班级的概率 解：（1）该校班级个数为 420%20（个）， 只有 2 名留守儿童的班级个数为：20（2+3+4+5+4）2（个）， 该校平均每班留守儿童的人数为： 4（名）， 补图如下： ； （2）由（1）得只有 2 名留守儿童的班级有 2 个，共 4 名学生设 A1，A2来自一个班， B1，B

28、2来自一个班， 由树状图可知，共有 12 种可能的情况，并且每种结果出现的可能性相等，其中来自一个 班的共有 4 种情况， 则所选两名留守儿童来自同一个班级的概率为： 五、（共 2 小题，每小题 10 分，满分 20 分） 19已知一次函数 y1x+m 的图象与反比例函数 y2的图象交于 A、B 两点已知当 x1 时，y1y2；当 0x1 时，y1y2 （1）求一次函数的解析式； （2）已知双曲线在第一象限上有一点 C 到 y 轴的距离为 3，求ABC 的面积 【分析】（1）首先根据 x1 时，y1y2，0x1 时，y1y2确定点 A 的横坐标，然后 代入反比例函数解析式求出点 A 的纵坐标，

29、从而得到点 A 的坐标，再利用待定系数法求 直线解析式解答； （2） 根据点 C 到 y 轴的距离判断出点 C 的横坐标， 代入反比例函数解析式求出纵坐标， 从而得到点 C 的坐标，过点 C 作 CDx 轴交直线 AB 于 D，求出点 D 的坐标，然后得到 CD 的长度，再联立一次函数与双曲线解析式求出点 B 的坐标，然后ABC 的面积 ACD 的面积+BCD 的面积，列式进行计算即可得解 解：（1）当 x1 时，y1y2；当 0x1 时，y1y2， 点 A 的横坐标为 1， 代入反比例函数解析式，y， 解得 y6， 点 A 的坐标为（1，6）， 又点 A 在一次函数图象上， 1+m6， 解得

30、 m5， 一次函数的解析式为 y1x+5； （2）第一象限内点 C 到 y 轴的距离为 3， 点 C 的横坐标为 3， y2， 点 C 的坐标为（3，2）， 过点 C 作 CDx 轴交直线 AB 于 D， 则点 D 的纵坐标为 2， x+52， 解得 x3， 点 D 的坐标为（3，2）， CD3（3）3+36， 点 A 到 CD 的距离为 624， 联立， 解得（舍去）， 点 B 的坐标为（6，1）， 点 B 到 CD 的距离为 2（1）2+13， SABCSACD+SBCD64+6312+921 20已知：如图，在平行四边形 ABCD 中，点 M 在边 AD 上，且 AMDMCM、BA 的延

31、 长线相交于点 E求证： （1）AEAB； （2）如果 BM 平分ABC，求证：BMCE 【分析】（1）由在平行四边形 ABCD 中，AMDM，易证得AEMDCM（AAS）， 即可得 AECDAB； （2）由 BM 平分ABC，易证得BCE 是等腰三角形，根据等腰三角形三线合一的性质 可得出结论 【解答】证明：（1）四边形 ABCD 是平行四边形， ABCD，ABCD， EDCM， 在AEM 和DCM 中， ， AEMDCM（AAS）， AECD， AEAB； （2）BM 平分ABC， ABMCBM， 四边形 ABCD 是平行四边形， ADBC， CBMAMB， ABMAMB， ABAM， A

32、BAE，AMDM， 点 M 是 AD 的中点， BC2AM， BCBE， BCE 是等腰三角形 BM 平分ABC， BMCE 六、（本题满分 12 分） 21 （1） 解下列方程： 根为 x11， x22 ； 根为 x12， x23 ； 根为 x13，x24 ； （2）根据这类方程特征，写出第 n 个方程为 x+2n+1 ，其根为 x1n，x2 n+1 （3）请利用（2）的结论，求关于 x 的方程（n 为正整数）的根 【分析】 （1） 首先去分母，即可化成一元二次方程， 解方程求得 x 的值，然后进行检验， 即可求得方程的解； （2）根据（1）中的三个方程的特点以及解的关系即可求解； （3）根

33、据（3）的结果，把所求的方程化成 x3+2n+1 的形式，把 x3 当作 一个整体即可求解 解：（1）去分母，得：x2+23x，即 x23x+20，（x1）（x2）0， 则 x10，x20， 解得：x11，x22， 经检验：x11，x22 都是方程的解； 去分母，得：x2+65x，即 x25x+60，（x2）（x3）0， 则 x20，x30， 解得：x12，x23， 经检验：x12，x23 是方程的解； 去分母，得：x2+127x，即 x27x+120，（x3）（x4）0， 则 x13，x24， 经检验 x13，x24 是方程的解； （2）出第 n 个方程为 x+2n+1，解是 x1n，x2n

34、+1； （3）， 即 x3+2n+1， 则 x3n 或 x3n+1， 解得：x1n+3，x2n+4 七、（本题满分 12 分） 22为了扶持大学生自主创业，市政府提供了 80 万元无息贷款，用于某大学生开办公司生 产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款已 知该产品的生产成本为每件 40 元，员工每人每月的工资为 2500 元，公司每月需支付其 它费用 15 万元该产品每月销售量 y（万件）与销售单价 x（元）之间的函数关系如图 所示 （1）求月销售量 y（万件）与销售单价 x（元）之间的函数关系式； （2）当销售单价定为 50 元时，为保证公司月利润达到 5

35、万元（利润销售额生产成 本员工工资其它费用），该公司可安排员工多少人？ （3）若该公司有 80 名员工，则该公司最早可在几个月后还清无息贷款？ 【分析】（1）从图中看，这是一个分段一次函数，40x60 和 60x100 时，函数的 表达式不同，每段函数都经过两点，使用待定系数法即可求出函数关系式； （2）利用（1）中的函数关系，当销售单价定为 50 元时，可计算出月销售量，设可安排 员工 m 人，利润销售额一生产成本员工工资其它费用，列出方程即可解； （3）先分情况讨论出利润的最大值，即可求解 解：（1）当 40x60 时，令 ykx+b， 则， 解得， 故， 同理，当 60x80 时， 故

36、y； （2）设公司可安排员工 a 人，定价 50 元时， 由 5（50+8）（5040）150.25a， 得 30150.25a5， 解得 a40， 所以公司可安排员工 40 人； （3）当 40x60 时， 利润 w1（x+8）（x40）1520 （x60）2+5， 则当 x60 时，wmax5 万元； 当 60x100 时， w2（x+5）（x40）150.2580 （x70）2+10， x70 时，wmax10 万元， 要尽早还清贷款，只有当单价 x70 元时，获得最大月利润 10 万元， 设该公司 n 个月后还清贷款，则 10n80， n8，即 n8 为所求 八、（本题满分 14 分）

37、 23 在锐角ABC 中， AB4， BC5， ACB45， 将ABC 绕点 B 按逆时针方向旋转， 得到A1BC1 （1）如图 1，当点 C1在线段 CA 的延长线上时，求CC1A1的度数； （2）如图 2，连接 AA1，CC1若ABA1的面积为 4，求CBC1的面积； （3）如图 3，点 E 为线段 AB 中点，点 P 是线段 AC 上的动点，在ABC 绕点 B 按逆时 针方向旋转过程中，点 P 的对应点是点 P1，求线段 EP1长度的最大值与最小值 【分析】（1）根据旋转的性质解答； （2）运用全等三角形和相似三角形的性质，求出（）2（）2， 进而解决问题； （3） 过点 B 作 BDA

38、C， D 为垂足， 因为ABC 为锐角三角形， 所以点 D 在线段 AC 上， 在 RtBCD 中，BDBCsin45；然后进行讨论，求得线段 EP1长度的最大值 与最小值 解：（1）由旋转的性质可得：A1C1BACB45，BCBC1， 所以CC1BC1CB45， 所以CC1A1CC1B+A1C1B45+4590 （2）因为ABCA1BC1， 所以 BABA1，BCBC1，ABCA1BC1， ，ABC+ABC1A1BC1+ABC1， 所以ABA1CBC1， 所以ABA1CBC1 所以，（）2（）2， 因为 SABA14， 所以 SCBC1； （3）如图 ，过点 B 作 BDAC，D 为垂足， 因为ABC 为锐角三角形，所以点 D 在线段 AC 上， 在 RtBCD 中，BDBCsin45； 当 P 在 AC 上运动与 AB 垂直的时候，ABC 绕点 B 旋转，使点 P 的对应点 P1在线段 AB 上时，EP1最小，最小值为：EP1BP1BEBDBE2； 当 P 在 AC 上运动至点 C，ABC 绕点 B 旋转，使点 P 的对应点 P1在线段 AB 的延长 线上时，EP1最大，最大值为：EP1BC+BE2+57