1、绝密启用前绝密启用前 2020 年四川省巴中市平昌县镇龙中学中考数学模拟试卷年四川省巴中市平昌县镇龙中学中考数学模拟试卷 注意事项： 1答题前填写好自己的姓名、班级、考号等信息 2请将答案正确填写在答题卡上，在试卷上作答无效，选择题需使用 2B 铅笔填涂 一选择题（共一选择题（共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 1下列各数中，是无理数的是（ ） Acos30 B（x）0 C D 2给出下列各式：（2） 01；（a+b）2a2+b2；（3ab3）29a2b6； 9，其中正确的是（ ） A B C D 3能铺满地面的正多边形的组合是（ ） A正五边形和正方形
2、B正六边形和正方形 C正八边形和正方形 D正十边形和正方形 4期末考试后，办公室里有两位数学老师正在讨论他们班的数学考试成绩，林老师：“我 班的学生考得还不错，有一半的学生考 79 分以上，一半的学生考不到 79 分”王老师： “我班大部分的学生都考在 80 分到 85 分之间喔”依照上面两位老师所叙述的话你认 为林、王老师所说的话分别针对（ ） A平均数、众数 B平均数、极差 C中位数、方差 D中位数、众数 5已知关于 x 的不等式（2a）x1 的解集是 x；则 a 的取值范围是（ ） Aa0 Ba0 Ca2 Da2 6 如图， 点 E 是ABC 的内心， AE 的延长线和ABC 的外接圆相
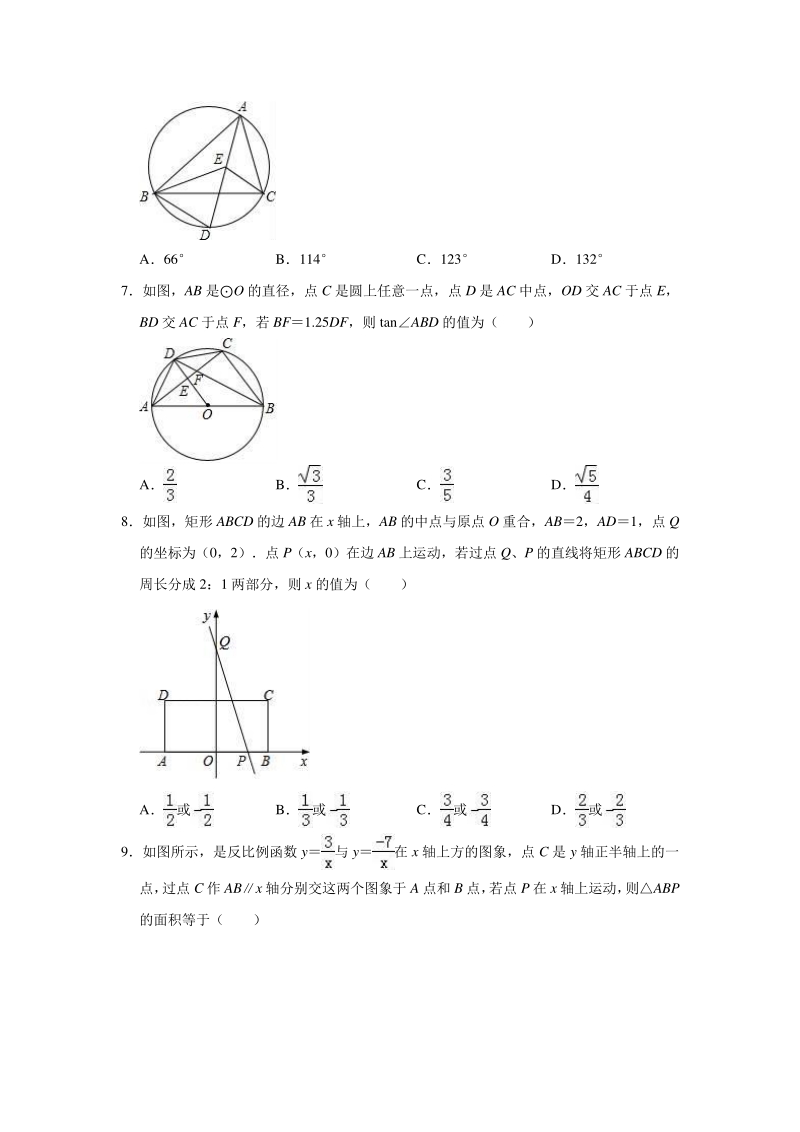
3、交于点 D 连接 BD， BE， CE，若CBD33，则BEC（ ） A66 B114 C123 D132 7如图，AB 是O 的直径，点 C 是圆上任意一点，点 D 是 AC 中点，OD 交 AC 于点 E， BD 交 AC 于点 F，若 BF1.25DF，则 tanABD 的值为（ ） A B C D 8如图，矩形 ABCD 的边 AB 在 x 轴上，AB 的中点与原点 O 重合，AB2，AD1，点 Q 的坐标为（0，2）点 P（x，0）在边 AB 上运动，若过点 Q、P 的直线将矩形 ABCD 的 周长分成 2：1 两部分，则 x 的值为（ ） A或 B或 C或 D或 9如图所示，是反比
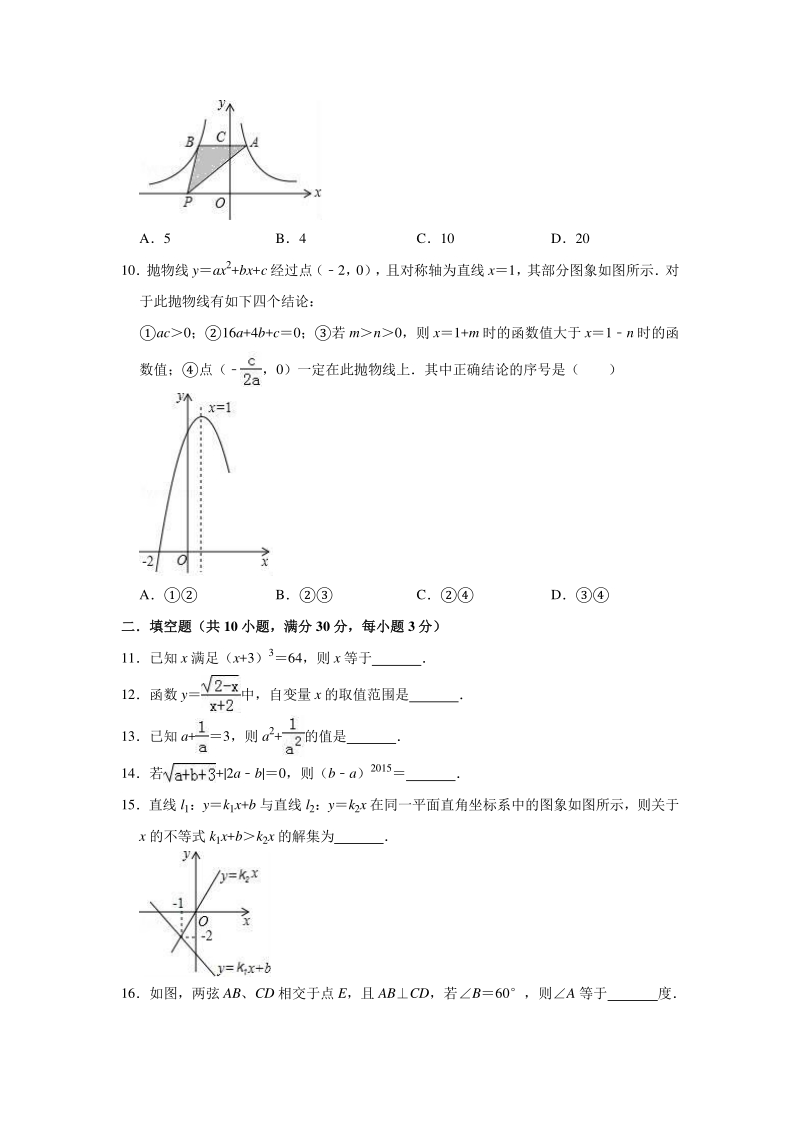
4、例函数 y与 y在 x 轴上方的图象，点 C 是 y 轴正半轴上的一 点， 过点 C 作 ABx 轴分别交这两个图象于 A 点和 B 点， 若点 P 在 x 轴上运动， 则ABP 的面积等于（ ） A5 B4 C10 D20 10 抛物线 yax2+bx+c 经过点 （2， 0） ， 且对称轴为直线 x1， 其部分图象如图所示 对 于此抛物线有如下四个结论： ac0；16a+4b+c0；若 mn0，则 x1+m 时的函数值大于 x1n 时的函 数值；点（，0）一定在此抛物线上其中正确结论的序号是（ ） A B C D 二填空题（共二填空题（共 10 小题，满分小题，满分 30 分，每小题分，每
5、小题 3 分）分） 11已知 x 满足（x+3）364，则 x 等于 12函数 y中，自变量 x 的取值范围是 13已知 a+3，则 a2+的值是 14若+|2ab|0，则（ba）2015 15直线 l1：yk1x+b 与直线 l2：yk2x 在同一平面直角坐标系中的图象如图所示，则关于 x 的不等式 k1x+bk2x 的解集为 16如图，两弦 AB、CD 相交于点 E，且 ABCD，若B60，则A 等于 度 17已知菱形的周长为 20cm，一条对角线长为 6cm，则这个菱形的面积是 cm2 18 如图， 在 RtABC 中， ACB90， ACBC1， E 为 BC 边上的一点， 以 A 为
6、圆心， AE 为半径的圆弧交 AB 于点 D， 交 AC 的延长于点 F， 若图中两个阴影部分的面积相等， 则 AF2为 19在实数范围内因式分解：2x24x1 20如图，等边BCP 在正方形 ABCD 内，则APD 度 三解答题（共三解答题（共 11 小题，满分小题，满分 90 分）分） 21（6 分）计算：4sin60|1|+（1）0+ 22（7 分）已知关于 x 的一元二次方程 x2+ax+a20 （1）若该方程的一个根为2，求 a 的值及该方程的另一根； （2）求证：无论 a 取何实数，该方程都有两个不相等的实数根 23（7 分）先化简：（ +1）+，然后从2x1 的范围内选取 一个合
7、适的整数作为 x 的值代入求值 24（8 分）如图，在平行四边形 ABCD 中，点 E 在边 BC 上，点 F 在边 AD 的延长线上， 且 DFBE，求证：BDEF 25（8 分）为了贯彻“减负增效”精神，掌握九年级 600 名学生每天的自主学习情况，某 校学生会随机抽查了九年级的部分学生，并调查他们每天自主学习的时间根据调查结 果，制作了两幅不完整的统计图（图 1，图 2），请根据统计图中的信息回答下列问题： （1）本次调查的学生人数是 人； （2）图 2 中 是 度，并将图 1 条形统计图补充完整； （3）请估算该校九年级学生自主学习时间不少于 1.5 小时有 人； （4）老师想从学习效
8、果较好的 4 位同学（分别记为 A、B、C、D，其中 A 为小亮）随机 选择两位进行学习经验交流，用列表法或树状图的方法求出选中小亮 A 的概率 26（6 分）在如图所示的方格中，每个小正方形的边长为 1，点 A、B、C 在方格纸中小正 方形的顶点上 （1）按下列要求画图： 过点 A 画 BC 的平行线 DF； 过点 C 画 BC 的垂线 MN； 将ABC 绕 A 点顺时针旋转 90 （2）计算ABC 的面积 27 （8 分）某商场一种商品的进价为每件 30 元，售价为每件 40 元每天可以销售 48 件， 为尽快减少库存，商场决定降价促销 （1） 若该商品连续两次下调相同的百分率后售价降至每
9、件 32.4 元， 求两次下降的百分率； （2）经调查，若该商品每降价 0.5 元，每天可多销售 4 件，那么每天要想获得 510 元的 利润，每件应降价多少元？ 28（8 分）如图，在ABC 中，ABAC，以 AC 为直径作O 交 BC 于点 D，过点 D 作 O 的切线 EF，交 AB 和 AC 的延长线于 E、F （1）求证：FEAB； （2）当 AE6，sinCFD时，求 EB 的长 29（10 分）如图，一次函数 yax+b 与反比例函数 y的图象交于 A、B 两点，点 A 坐 标为（m，2），点 B 坐标为（4，n），OA 与 x 轴正半轴夹角的正切值为，直线 AB 交 y 轴于点
10、 C，过 C 作 y 轴的垂线，交反比例函数图象于点 D，连接 OD、BD （1）求一次函数与反比例函数的解析式； （2）求四边形 OCBD 的面积 30（10 分）如图，从热气球 C 上测得两建筑物 A、B 底部的俯角分别为 30和 60 度如 果这时气球的高度 CD 为 90 米 且点 A、 D、 B 在同一直线上， 求建筑物 A、 B 间的距离 31（12 分）如图，直线 AB 和抛物线的交点是 A（0，3），B（5，9），已知抛物线的 顶点 D 的横坐标是 2 （1）求抛物线的解析式及顶点坐标； （2）在 x 轴上是否存在一点 C，与 A，B 组成等腰三角形？若存在，求出点 C 的坐标
11、， 若不在，请说明理由； （3）在直线 AB 的下方抛物线上找一点 P，连接 PA，PB 使得PAB 的面积最大，并求 出这个最大值 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 1【分析】分别根据无理数、有理数的定义即可判定选择项 【解答】解：A、cos30，故 A 符合题意； B、（x）01，故 B 不符合题意； C、是有理数，故 C 不符合题意； D、8 是有理数，故 D 不符合题意； 故选：A 【点评】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不 循环小数为无理数如 ，0.8
12、080080008（每两个 8 之间依次多 1 个 0）等形式 2【分析】根据零指数幂：a01（a0）；完全平方公式：（ab）2a22ab+b2；积 的乘方法则：把每一个因式分别乘方，再把所得的幂相乘；负整数指数幂：ap（a 0，p 为正整数）进行计算即可 【解答】解：（2）01； （a+b）2a2+2ab+b2； （3ab3）29a2b6； 9， 故原题计算正确的有 3 个，是， 故选：A 【点评】此题主要考查了零指数幂、积的乘方、完全平方公式和负整数指数幂，关键是 熟练掌握各计算法则 3【分析】分别求出各个多边形每个内角的度数，然后根据围绕一点拼在一起的多边形的 内角加在一起恰好组成一个周
13、角判断即可 【解答】 解： 正五边形每个内角是 1803605108， 正方形的每个内角是 90， 108m+90n360，n4m，显然 m 取任何正整数时，n 不能得正整数，故不能铺满； 正方形的每个内角是 90，正六边形的每个内角是 120 度90m+120n360，m4 n，显然 n 取任何正整数时，m 不能得正整数，故不能铺满； 正方形的每个内角是 90，正八边形的每个内角为：1803608135，90 +2135360正八边形和正方形能铺满 故选：C 【点评】几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰 好组成一个周角 4 【分析】 根据两位老师的说法中的有一
14、半的学生考 79 分以上， 一半的学生考不到 79 分， 可以判断 79 分是中位数，大部分的学生都考在 80 分到 85 分之间，可以判断众数 【解答】解：有一半的学生考 79 分以上，一半的学生考不到 79 分， 79 分是这组数据的中位数， 大部分的学生都考在 80 分到 85 分之间， 众数在此范围内 故选：D 【点评】本题考查了统计量的选择，解题的关键是抓住题目中的关键词语 5 【分析】 根据已知不等式的解集， 结合 x 的系数确定出 2a 为负数， 求出 a 的范围即可 【解答】解：关于 x 的不等式（2a）x1 的解集是 x， 2a0， 解得：a2 故选：D 【点评】此题考查了不
15、等式的解集，熟练掌握不等式的基本性质是解本题的关键 6【分析】根据圆周角定理可求CAD33，再根据三角形内心的定义可求BAC，再 根据三角形内角和定理和三角形内心的定义可求EBC+ECB，再根据三角形内角和定 理可求BEC 的度数 【解答】解：在O 中，CBD33， CAD33， 点 E 是ABC 的内心， BAC66， EBC+ECB（18066）257， BEC18057123 故选：C 【点评】考查了三角形的内切圆与内心，圆周角定理，三角形内角和定理，关键是得到 EBC+ECB 的度数 7【分析】由ADFBDA，推出 AD2DFDB，由 BF1.25DF，可以假设 DF4m， 则 BF5
16、m，BD9m，可得 AD6m，根据 tanABD计算即可解决问题 【解答】解：， DAFDBA， ADFADB， ADFBDA， ， AD2DFDB， BF1.25DF， 可以假设 DF4m，则 BF5m，BD9m， AD236m2， AD0， AD6m， AB 是直径， ADB90， tanABD， 故选：A 【点评】本题考查圆周角定理，相似三角形的判定和性质，锐角三角函数等知识，解题 的关键是学会利用参数解决问题，属于中考常考题型 8 【分析】分类讨论：点 P 在 OA 上和点 P 在 OB 上两种情况根据题意列出比例关系式， 直接解答即可得出 x 得出值 【解答】解：如图，AB 的中点与
17、原点 O 重合，在矩形 ABCD 中，AB2，AD1， A（1，0），B（1，0），C（1，1） 当点 P 在 OB 上时易求 G（，1） 过点 Q、P 的直线将矩形 ABCD 的周长分成 2：1 两部分， 则 AP+AD+DG3+x，CG+BC+BP3x， 由题意可得：3+x2（3x）， 解得 x 由对称性可求当点 P 在 OA 上时，x 故选：D 【点评】本题主要考查了一次函数的综合题，解答要注意数形结合思想的运用，是各地 中考的热点，同学们要加强训练，属于中档题 9【分析】设点 A（a，），可得点 B 坐标（，），即可求ABP 的面积 【解答】解：设点 A（a，） ABx 轴 点 B 纵
18、坐标为，且点 B 在反比例函数 y图象上， 点 B 坐标（，） SABP （a+） 5 故选：A 【点评】本题考查了反比例函数图象上点的坐标特征，设点 A（a，），利用字母 a 表 示 AB 的长度和线段 AB 上的高，是本题的关键 10【分析】利由抛物线的位置可对进行判断；利用抛物线的对称性得到抛物线与 x 轴 的一个交点坐标为（4，0），代入解析式则可对进行判断；由抛物线的对称性和二次 函数的性质可对进行判断；抛物线的对称性得出点（2，0）的对称点是（4，0）， 由 c8a 即可得出4，则可对进行判断 【解答】解：抛物线开口向下， a0， 抛物线交 y 轴的正半轴， c0， ac0，故错误
19、； 抛物线的对称轴为直线 x1， 而点（2，0）关于直线 x1 的对称点的坐标为（4，0）， 16a+4b+c0，故正确； 抛物线开口向下，对称轴为直线 x1， 横坐标是 1n 的点的对称点的横坐标为 1+n， 若 mn0， 1+m1+n， x1+m 时的函数值小于 x1n 时的函数值，故错误； 抛物线的对称轴为1， b2a， 抛物线为 yax22ax+c， 抛物线 yax2+bx+c 经过点（2，0）， 4a+4a+c0，即 8a+c0， c8a， 4， 点（2，0）的对称点是（4，0）， 点（，0）一定在此抛物线上，故正确， 故选：C 【点评】本题考查了二次函数图象与系数的关系：对于二次函
20、数 yax2+bx+c（a0）， 二次项系数 a 决定抛物线的开口方向和大小： 当 a0 时， 抛物线向上开口； 当 a0 时， 抛物线向下开口；一次项系数 b 和二次项系数 a 共同决定对称轴的位置：当 a 与 b 同号 时（即 ab0），对称轴在 y 轴左； 当 a 与 b 异号时（即 ab0），对称轴在 y 轴右； 常数项 c 决定抛物线与 y 轴交点位置：抛物线与 y 轴交于（0，c）；抛物线与 x 轴交点个 数由决定：b24ac0 时，抛物线与 x 轴有 2 个交点；b24ac0 时，抛物 线与 x 轴有 1 个交点；b24ac0 时，抛物线与 x 轴没有交点 二填空题（共二填空题（
21、共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 11【分析】根据立方根的定义得出关于 x 的方程，解之可得 【解答】解：（x+3）364， x+34， 解得：x1， 故答案为：1 【点评】本题主要考查立方根，解题的关键是掌握立方根的定义与解一元一次方程的能 力 12【分析】由二次根式中被开方数为非负数且分母不等于零求解可得 【解答】解：根据题意，得：， 解得：x2 且 x2， 故答案为：x2 且 x2 【点评】 本题主要考查函数自变量的取值范围， 函数自变量的范围一般从三个方面考虑： （1）当函数表达式是整式时，自变量可取全体实数； （2）当函数表达式是分式时，考虑分
22、式的分母不能为 0； （3）当函数表达式是二次根式时，被开方数非负 13【分析】把已知条件两边平方，然后整理即可求解完全平方公式：（ab）2a2 2ab+b2 【解答】解：a+3， a2+2+ 9， a2+927 故答案为：7 【点评】本题主要考查了完全平方公式，利用公式把已知条件两边平方是解题的关键 14【分析】利用非负数的性质列出方程组，求出方程组的解得到 a 与 b 的值，代入原式计 算即可得到结果 【解答】解： +|2ab|0， ， 解得：， 则原式1， 故答案为：1 【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元 法与加减消元法 15【分析】求关于 x
23、的不等式 k1x+bk2x 的解集就是求：能使函数 yk1x+b 的图象在函 数 yk2x 的上边的自变量的取值范围 【解答】 能使函数yk1x+b的图象在函数yk2x的上边时的自变量的取值范围是x1 故关于 x 的不等式 k1x+bk2x 的解集为：x1 故答案为：x1 【点评】本题考查了一次函数与一元一次不等式的关系，根据不等式的问题转化为比较 函数值的大小的问题是解决本题的关键 16【分析】由同弧所对圆周角相等得出CB60，再根据垂直知AEC90， 利用直角三角形两锐角相等得出答案 【解答】解：B60， CB60， ABCD， AEC90， A30， 故答案为：30 【点评】本题主要考查
24、圆周角定理，解题的关键是掌握圆周角定理：在同圆或等圆中， 同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半 17【分析】根据菱形的性质，先求另一条对角线的长度，再运用菱形的面积等于对角线乘 积的一半求解 【解答】解：如图，在菱形 ABCD 中，BD6 菱形的周长为 20，BD6， AB5，BO3， AO4，AC8 面积 S6824 故答案为 24 【点评】此题考查了菱形的性质及面积求法，难度不大 18【分析】若两个阴影部分的面积相等，那么ABC 和扇形 ADF 的面积就相等，可分别 表示出两者的面积，然后列出方程即可求出 AF 的长度 【解答】解：图中两个阴影部分的面积相等， S 扇
25、形ADFSABC，即： ACBC， 又ACBC1， AF2 故答案为： 【点评】此题主要考查了扇形面积的计算方法及等腰直角三角形的性质，能够根据题意 得到ABC 和扇形 ADF 的面积相等，是解决此题的关键，难度一般 19【分析】令原式为 0 求出 x 的值，即可确定出因式分解的结果 【解答】解：令 2x24x10， 这里 a2，b4，c1， 16+824， x， 则原式2（x）（x）， 故答案为：2（x）（x） 【点评】此题考查了实数范围内分解因式，熟练掌握因式分解的方法是解本题的关键 20 【分析】由正方形的性质和等边三角形的性质得出 ABBPCPCD，ABPDCP 30，由三角形内角和定
26、理求出BAPBPACDPCPD75，再求出 PADPDA15，然后由三角形内角和定理求出APD 即可 【解答】解：四边形 ABCD 是正方形， ABBCCDDA，BADABCBCDCDA90， BCP 是等边三角形， BPCPBC，PBCBCPBPC60， ABBPCPCD，ABPDCP906030， BAPBPACDPCPD（18030）75， PADPDA907515， APD1801515150； 故答案为：150 【点评】本题考查了正方形的性质、等边三角形的性质、三角形内角和定理、等腰三角 形的性质； 熟练掌握正方形和等边三角形的性质， 并能进行推理计算是解决问题的关键 三解答题（共三
27、解答题（共 11 小题，满分小题，满分 90 分）分） 21【分析】将特殊锐角三角函数值代入、计算绝对值、零指数幂、化简二次根式，再进一 步计算可得 【解答】解：原式41+1+4 2+4 6 【点评】本题主要考查实数的运算，解题的关键是掌握特殊锐角三角函数值、绝对值性 质、零指数幂、二次根式性质 22【分析】（1）将 x2 代入方程 x2+ax+a20 得到 a 的值，再解方程求出另一根； （2）写出根的判别式，配方后得到完全平方式，进行解答 【解答】解：（1）将 x2 代入方程 x2+ax+a20 得，42a+a20， 解得，a2； 方程为 x2+2x0，解得 x10，x22， 即方程的另一
28、根为 0； （2）a24（a2）a24a+8a24a+4+4（a2）2+40， 不论 a 取何实数，该方程都有两个不相等的实数根 【点评】本题考查了根的判别式一元二次方程根的情况与判别式的关系： （1）0方程有两个不相等的实数根； （2）0方程有两个相等的实数根； （3）0方程没有实数根 同时考查了一元二次方程的解的定义 23【分析】根据分式的混合运算法则把原式化简，根据条件选择合适的值代入计算即可 【解答】解：原式（+）+ ， x1，且 x0， 可取 x2， 则原式8 【点评】本题考查的是分式的化简求值，掌握分式的混合运算法则与分式有意义的条件 是解题的关键 24【分析】只要证明四边形 DB
29、EF 是平行四边形即可解决问题 【解答】证明：四边形 ABCD 是平行四边形， ADBC， DFBE， 四边形 DBEF 是平行四边形， BDEF； 【点评】本题考查了平行四边形的判定与性质，解题的关键是熟练掌握平行四边形的判 定方法，属于中考常考题型 25【分析】（1）由自主学习的时间是 1 小时的有 12 人，占 30%，即可求得本次调查的 学生人数； （2）由36054，4035%14；即可求得答案； （3） 首先求得这 40 名学生自主学习时间不少于 1.5 小时的百分比， 然后可求得该校九年 级学生自主学习时间不少于 1.5 小时的人数； （4）首先根据题意画出树状图，然后由树状图求
30、得所有等可能的结果与选中小亮 A 的情 况，再利用概率公式求解即可求得答案 【解答】解：（1）自主学习的时间是 1 小时的有 12 人，占 30%， 1230%40， 故答案为：40； （2 分） （2）36054， 故答案为：54； 4035%14； 补充图形如图： 故答案为：54； （3）600330； （2 分） 故答案为：330； （4）画树状图得： 共有 12 种等可能的结果，选中小亮 A 的有 6 种， P（A）（2 分） 【点评】本题考查的是用列表法或画树状图法求概率与扇形统计图、条形统计图的知 识列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步 完成的事
31、件，树状图法适合两步或两步以上完成的事件注意概率所求情况数与总情 况数之比 26【分析】（1）利用 BC 为小方格正方形的对角线，画 DFBC，MNBC，利用网格特 点和旋转的性质画出 B、C 旋转后的对应点 B、C，从而得到ABC； （2）利用三角形面积公式计算 【解答】解：（1）如图，DF、MN、ABC为所作； （2）ABC 的面积211 【点评】本题考查了作图旋转变换：根据旋转的性质可知，对应角都相等都等于旋转 角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法， 找到对应点，顺次连接得出旋转后的图形 27【分析】（1）设每次降价的百分率为 x，（1x）2为两次降
32、价的百分率，40 降至 32.4 就是方程的平衡条件，列出方程求解即可； （2）设每天要想获得 510 元的利润，且更有利于减少库存，则每件商品应降价 y 元，由 销售问题的数量关系建立方程求出其解即可 【解答】解：（1）设每次降价的百分率为 x 40（1x）232.4 x10%或 190%（190%不符合题意，舍去） 答： 该商品连续两次下调相同的百分率后售价降至每件 32.4 元， 两次下降的百分率啊 10%； （2）设每天要想获得 510 元的利润，且更有利于减少库存，则每件商品应降价 y 元，由 题意，得 （4030y）（4+48）510， 解得：y11.5，y22.5， 有利于减少库
33、存， y2.5 答：要使商场每月销售这种商品的利润达到 510 元，且更有利于减少库存，则每件商品 应降价 2.5 元 【点评】 此题主要考查了一元二次方程应用， 关键是根据题意找到等式两边的平衡条件， 这种价格问题主要解决价格变化前后的平衡关系，列出方程，解答即可 28【分析】（1）先证明 ODAB，得出ODFAEF，再由切线的性质得出ODF 90，证出AEF90，即可得出结论； （2）设 OAODOCr，先由三角函数求出 AF，再证明ODFAEF，得出对应边 成比例求出半径，得出 AB，即可求出 EB 【解答】（1）证明：连接 OD，如图所示： OCOD， OCDODC， ABAC， AC
34、BB， ODCB， ODAB， ODFAEF， EF 与O 相切， ODEF， ODF90， AEFODF90， EFAB； （2）解：设 OAODOCr， 由（1）知：ODAB，ODEF， 在 RtAEF 中，sinCFD，AE6， AF10， ODAB， ODFAEF， ， ， 解得 r， ABAC2r， EBABAE6 【点评】本题考查了切线的性质、相似三角形的判定与性质以及解直角三角形；熟练掌 握切线的性质，并能进行有关推理计算是解决问题的关键 29【分析】（1）根据正切值，可得 OE 的长，可得 A 点坐标，根据待定系数法，可得反 比例函数解析式，根据点的坐标满足函数解析式，可得 B
35、 点坐标，根据待定系数法，可 得一次函数解析式； （2）根据面积的和，可得答案 【解答】解：（1）如图： ， tanAOE， 得 OE6， A（6，2）， y的图象过 A（6，2）， ， 即 k12， 反比例函数的解析式为 y， B（4，n）在 y的图象上， 解得 n3， B（4，3）， 一次函数 yax+b 过 A、B 点， ， 解得， 一次函数解析式为 y1； （2）当 x0 时，y1， C（0，1）， 当 y1 时，1，x12， D（12，1）， sOCBDSODC+SBDC +|12|2| 6+12 18 【点评】本题考查了反比例函数与一次函数的交点问题，待定系数法求解析式的关键， 利
36、用面积的和差求解四边形的面积 30 【分析】 在图中两个直角三角形中， 都是知道已知角和对边， 根据正切函数求出邻边后， 相加求和即可 【解答】解：由已知，得ECA30，FCB60，CD90， EFAB，CDAB 于点 D AECA30，BFCB60 在 RtACD 中，CDA90，tanA， AD9090 在 RtBCD 中，CDB90，tanB， DB30 ABAD+BD90+30120 答：建筑物 A、B 间的距离为 120米 【点评】解决本题的关键是利用 CD 为直角ABC 斜边上的高，将三角形分成两个三角 形，然后求解分别在两三角形中求出 AD 与 BD 的长 31 【分析】 （1）
37、 抛物线的顶点 D 的横坐标是 2， 则 x2， 抛物线过是 A （0， 3） ， 则：函数的表达式为：yax2+bx3，把 B 点坐标代入函数表达式，即可求解； （2）分 ABAC、ABBC、ACBC，三种情况求解即可； （3）由 SPABPHxB，即可求解 【解答】解：（1）抛物线的顶点 D 的横坐标是 2，则 x2， 抛物线过是 A（0，3），则：函数的表达式为：yax2+bx3， 把 B 点坐标代入上式得：925a+5b3， 联立、解得：a，b，c3， 抛物线的解析式为：yx2x3， 当 x2 时，y，即顶点 D 的坐标为（2，）； （2）A（0，3），B（5，9），则 AB13， 当
38、 ABAC 时，设点 C 坐标（m，0）， 则：（m）2+（3）2132，解得：m4， 即点 C 坐标为：（4，0）或（4，0）； 当 ABBC 时，设点 C 坐标（m，0）， 则：（5m）2+92132，解得：m5， 即：点 C 坐标为（5，0）或（52，0）， 当 ACBC 时，设点 C 坐标（m，0）， 则：点 C 为 AB 的垂直平分线于 x 轴的交点， 则点 C 坐标为（，0）， 故：存在， 点 C 的坐标为：（4，0）或（4，0）或（5 ，0）或（52，0） 或（，0）； （3）过点 P 作 y 轴的平行线交 AB 于点 H， 设：AB 所在的直线过点 A（0，3），则设直线 AB 的表达式为 ykx3， 把点 B 坐标代入上式，95k3，则 k， 故函数的表达式为：yx3， 设：点 P 坐标为（m， m2m3），则点 H 坐标为（m， m3）， SPABPHxB（m2+12m）， 当 m2.5 时，SPAB取得最大值为：， 答：PAB 的面积最大值为 【点评】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养要 会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长 度，从而求出线段之间的关系
