1、绝密启用前绝密启用前 2020 年四川省巴中市平昌县金山中学中考数学模拟试卷年四川省巴中市平昌县金山中学中考数学模拟试卷 注意事项： 1答题前填写好自己的姓名、班级、考号等信息 2请将答案正确填写在答题卡上，在试卷上作答无效，选择题需使用 2B 铅笔填涂 一选择题（共一选择题（共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 1在， ，sin30，tan30，（）0，这八个数中，整数 和无理数分别有（ ） A3 个，2 个 B2 个，2 个 C2 个，3 个 D3 个，3 个 2下列运算正确的是（ ） A01 B C（2A2）36A6 D（a+b）2a2+b2 3一幅美
2、丽的图案，在某个顶点处由四个边长相等的正多边形镶嵌而成，其中的三个分别 为正三边形，正四边形，正六边形，则另外一个为（ ） A正三角形 B正四边形 C正五边形 D正六边形 4 小明在参加区运动会前刻苦进行100米跑训练， 老师对他10次的训练成绩进行统计分析， 判断他的成绩是否稳定，则老师需要知道他这 10 次成绩的（ ） A众数 B方差 C平均数 D频数 5下列 x 的值不是不等式2x+40 的解，答案是（ ） A2 B3 C3.5 D10 6如图，点 I 和 O 分别是ABC 的内心和外心，则AIB 和AOB 的关系为（ ） AAIBAOB BAIBAOB C4AIBAOB360 D2AO
3、BAIB180 7已知 AB 是圆 O 的直径，AC 是弦，若 AB4，AC2，则 sinC 等于（ ） A B C D 8如图，已知直线 MN：ykx+2 交 x 轴负半轴于点 A，交 y 轴于点 B，BAO30，点 C 是 x 轴上的一点，且 OC2，则MBC 的度数为（ ） A75 B165 C75或 45 D75或 165 9如图，点 A 为反比例函数 y图象上一点，过 A 作 ABx 轴于点 B，连接 OA，则 ABO 的面积为（ ） A4 B2 C2 D无法确定 10 如图， 是二次函数 yax2+bx+c 图象的一部分， 其对称轴是 x1， 且过点 （3， 0） ， 下列说法：a
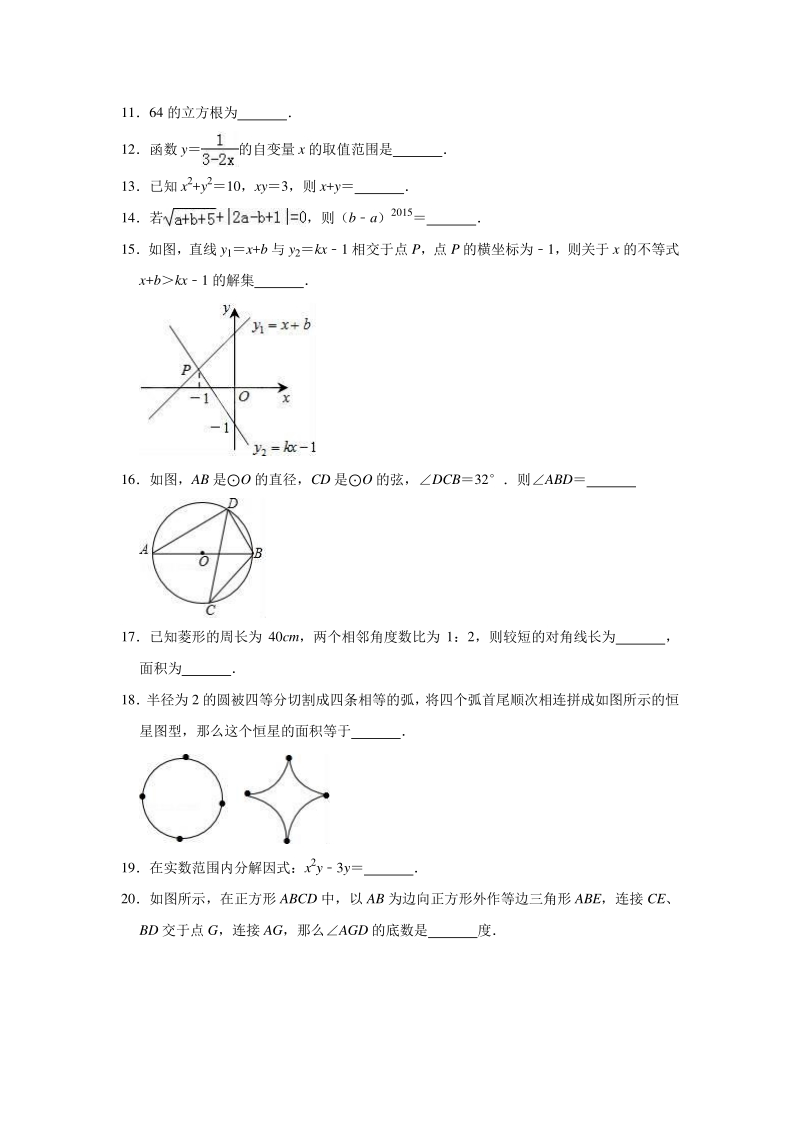
4、bc0；2ab0；8a+c0；若（5，y1），（3，y2）是抛物 线上两点，则 y1y2，其中正确的有（ ） A1 个 B2 个 C3 个 D4 个 二填空题（共二填空题（共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 1164 的立方根为 12函数 y的自变量 x 的取值范围是 13已知 x2+y210，xy3，则 x+y 14若 ，则（ba）2015 15如图，直线 y1x+b 与 y2kx1 相交于点 P，点 P 的横坐标为1，则关于 x 的不等式 x+bkx1 的解集 16如图，AB 是O 的直径，CD 是O 的弦，DCB32则ABD 17已知菱形的周长为 4
5、0cm，两个相邻角度数比为 1：2，则较短的对角线长为 ， 面积为 18 半径为 2 的圆被四等分切割成四条相等的弧， 将四个弧首尾顺次相连拼成如图所示的恒 星图型，那么这个恒星的面积等于 19在实数范围内分解因式：x2y3y 20如图所示，在正方形 ABCD 中，以 AB 为边向正方形外作等边三角形 ABE，连接 CE、 BD 交于点 G，连接 AG，那么AGD 的底数是 度 三解答题（共三解答题（共 11 小题，满分小题，满分 90 分）分） 21（6 分）计算sin45+3tan30（1）0 22（7 分）已知关于 x 的一元二次方程 x2mx30 （1）对于任意的实数 m，判断方程的根
6、的情况，并说明理由 （2）若 x1 是这个方程的一个根，求 m 的值和方程的另一根 23（7 分）先化简，然后从1x2 的范围内选取一个合适 的整数作为 x 的值代入求值 24（8 分）在ABCD 中，BCD 的平分线与 BA 的延长线相交于点 E，BHEC 于点 H， 求证：CHEH 25（8 分）“宜居襄阳”是我们的共同愿景，空气质量备受人们关注我市某空气质量监 测站点检测了该区域每天的空气质量情况， 统计了 2013 年 1 月份至 4 月份若干天的空气 质量情况，并绘制了如下两幅不完整的统计图 请根据图中信息，解答下列问题： （1）统计图共统计了 天的空气质量情况； （2）请将条形统计
7、图补充完整；空气质量为“优”所在扇形的圆心角度数是 ； （3）从小源所在环保兴趣小组 4 名同学（2 名男同学，2 名女同学）中，随机选取两名 同学去该空气质量监测站点参观， 则恰好选到一名男同学和一名女同学的概率是 26 （6 分）如图，在平面直角坐标系中，AOB 的三个顶点坐标分别为 A（1，0），O（0， 0），B（2，2）以点 O 为旋转中心，将AOB 逆时针旋转 90，得到A1OB1 （1）画出A1OB1； （2）直接写出点 A1和点 B1的坐标； （3）求线段 OB1的长度 27 （8 分） 甲商品的进价为每件 20 元， 商场将其售价从原来的每件 40 元进行两次调价 已 知该商
8、品现价为每件 32.4 元， （1）若该商场两次调价的降价率相同，求这个降价率； （2）经调查，该商品每降价 0.2 元，即可多销售 10 件已知甲商品售价 40 元时每月可 销售 500 件，若商场希望该商品每月能盈利 10000 元，且尽可能扩大销售量，则该商品 在现价的基础上还应如何调整？ 28（8 分）如图，以 AB 为直径的O 经过点 C，过点 C 作O 的切线交 AB 的延长线于 点 P，D 是O 上于点，且，弦 AD 的延长线交切线 PC 于点 E，连接 AC （1）求E 的度数； （2）若O 的直径为 5，sinP，求 AE 的长 29（10 分）如图，点 A（m，m+1），B
9、（m+3，m1）是反比例函数（x0）与一 次函数 yax+b 的交点求： （1）反比例函数与一次函数的解析式； （2）根据图象直接写出当反比例函数的函数值大于一次函数的函数值时 x 的取值范围 30（10 分）如图，为了测量电线杆的高度 AB，在离电线杆 25 米的 D 处，用高 1.20 米的 测角仪 CD 测得电线杆顶端 A 的仰角 22，求电线杆 AB 的高（精确到 0.1 米）参 考数据：sin220.3746，cos220.9272，tan220.4040，cot222.4751 31 （12 分）如图，在平面直角坐标系中，直线 ykx4k+4 与抛物线 yx2x 交于 A、 B 两
10、点 （1）直线总经过定点，请直接写出该定点的坐标； （2）点 P 在抛物线上，当 k时，解决下列问题： 在直线 AB 下方的抛物线上求点 P，使得PAB 的面积等于 20； 连接 OA，OB，OP，作 PCx 轴于点 C，若POC 和ABO 相似，请直接写出点 P 的坐标 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 1【分析】利用无理数是无限不循环小数，得出无理数的个数，利用整数的概念得出整数 的个数即可 【解答】解：整数有7，1，3，三个； 无理数有 tan30，2，三个， 故选：D 【点评】此题主要考
11、查了无理数、有理数的定义，无理数、有理数的辨别一直是学生易 混淆的难点，关键是根据无理数、整数的定义解答 2【分析】直接利用实数运算法则以及零指数幂的性质和积的乘方运算法则分别化简得出 答案 【解答】解：A、01，正确，符合题意； B、+，无法计算，故此选项错误； C、（2A2）38A6，故此选项错误； D、（a+b）2a2+b2+2ab，故此选项错误； 故选：A 【点评】此题主要考查了实数运算以及零指数幂的性质和积的乘方运算，正确掌握运算 法则是解题关键 3【分析】正多边形的组合能否进行平面镶嵌，关键是看位于同一顶点处的几个角之和能 否为 360若能，则说明才可能进行平面镶嵌；反之，则说明不
12、能进行平面镶嵌 【解答】解：正三角形、正四边形、正六边形的内角分别为 60、90、120， 又360609012090， 另一个为正四边形， 故选：B 【点评】本题考查平面密铺的知识，难度一般，解决此类题，可以记住几个常用正多边 形的内角，及能够用多种正多边形镶嵌的几个组合 4【分析】根据众数、平均数、频数、方差的概念分析 【解答】解：众数、平均数是反映一组数据的集中趋势，而频数是数据出现的次数，只 有方差是反映数据的波动大小的故为了判断成绩是否稳定，需要知道的是方差 故选：B 【点评】此题考查统计学的相关知识注意：方差是用来衡量一组数据波动大小的量， 方差越大，表明这组数据偏离平均数越大，即
13、波动越大，数据越不稳定；反之，方差越 小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定 5【分析】求出不等式的解集，即可作出判断 【解答】解：不等式2x+40， 解得：x2， 则2 不是不等式的解 故选：A 【点评】此题考查了不等式的解集，求出不等式的解集是解本题的关键 6【分析】根据圆周角定义，以及内心的定义，可以利用C 表示出AIB 和AOB，即 可得到两个角的关系 【解答】解：点 O 是ABC 的外心， AOB2C， CAOB， 点 I 是ABC 的内心， IABCAB，IBACBA， AIB180（IAB+IBA） 180（CAB+CBA）， 180（180C
14、） 90+C， 2AIB180+C， AOB2C， AIB90+AOB，即 4AIBAOB360 故选：C 【点评】 本题考查了圆周角定理以及三角形的内心的性质， 正确利用C 表示AIB 的度 数是关键 7【分析】如图，连接 BC求出A，再证明AACO 即可解决问题 【解答】解：如图，连接 BC AB 是直径， ACB90， cosA， A30， OAOC， OCAA30， sinOCAsin30 故选：B 【点评】 本题考查圆周角定理， 解直角三角形等知识， 解题的关键是熟练掌握基本知识， 属于中考常考题型 8【分析】分两种情况考虑：C 点在 x 轴正半轴；C 点在 x 轴负半轴分别计算出
15、MBO、OBC 度数，两个角的和差即为所求度数 【解答】解：由已知可得MBC120 如图，分两种情况考虑： 当点 C 在 x 轴正半轴上时， C1BO45，MBC11204575； 当点 C 在 x 轴负半轴上时， MBC2120+45165 故选：D 【点评】本题主要考查了一次函数图象的性质以及分类讨论思想 9【分析】根据过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成 的直角三角形面积 S 是个定值，即 S|k|即可求解 【解答】解：ABO 的面积是：|4|2 故选：C 【点评】本题主要考查了反比例函数 y中 k 的几何意义，即过双曲线上任意一点引 x 轴、y 轴垂线，所得
16、三角形面积为|k|，是经常考查的一个知识点；这里体现了数形结合 的思想，做此类题一定要正确理解 k 的几何意义 10【分析】根据二次函数的图象与性质即可求出答案 【解答】解：由对称轴可知：0， ab0， 由抛物线与 y 轴的交点可知：c0， abc0，故正确； 由图象可知：1， b2a， 2ab0，故正确； （3，0）关于直线 x1 的对称点为（1，0）， 令 x1，ya+b+c0， c3a， a0， 8a+c5a0，故正确； （5，y1）关于直线 x1 的对称点（3，y1）， 若（5，y1），（3，y2）是抛物线上两点，则 y1y2， 故正确； 故选：D 【点评】本题考查二次函数的图象与性质
17、，解题的关键是熟练运用数形结合的思想，本 题属于中等题型 二填空题（共二填空题（共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 11【分析】利用立方根定义计算即可得到结果 【解答】解：64 的立方根是 4 故答案为：4 【点评】此题考查了立方根，熟练掌握立方根的定义是解本题的关键 12【分析】求函数自变量的取值范围，就是求函数解析式有意义的条件，分式有意义的条 件是：分母不等于 0 【解答】解：根据题意知 32x0， 解得：x， 故答案为：x 【点评】本题主要考查自变量得取值范围的知识点，当函数表达式是分式时，考虑分式 的分母不能为 0 13【分析】根据完全平方公式即
18、可求出答案 【解答】解：由完全平方公式可得：（x+y）2x2+y2+2xy， x2+y210，xy3 （x+y）216 x+y4， 故答案为：4 【点评】本题考查完全平方公式，解题的关键是熟练运用完全平方公式，本题属于基础 题型 14【分析】根据已知等式，利用非负数的性质求出 a 与 b 的值，代入原式计算即可得到结 果 【解答】解： +|2ab+1|0， ， +得：3a6，即 a2， 把 a2 代入得：b3， 则原式（3+2）2015（1）20151 故答案为：1 【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元 法与加减消元法 15【分析】观察函数图象得到，当
19、x1，函数 yx+b 的图象都在函数 ykx1 图象的 上方，于是可得到关于 x 的不等式 x+bkx1 的解集 【解答】解：当 x1，函数 yx+b 的图象在函数 ykx1 图象的上方， 所以关于 x 的不等式 x+bkx1 的解集为 x1 故答案为：1 【点评】本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函 数 yax+b 的值大于（或小于）0 的自变量 x 的取值范围；从函数图象的角度看，就是确 定直线 ykx+b 在 x 轴上（或下）方部分所有的点的横坐标所构成的集合 16【分析】根据同弧所对的圆周角相等，求出DCBA32，再根据直径所对的圆 周角为 90，求出A
20、BD 的度数 【解答】解：DCB32， A32， AB 为O 直径， ADB90， 在 RtABD 中， ABD903258 故答案为：58 【点评】 本题考查了圆周角定理， 知道同弧所对的圆周角相等和直径所对的圆周角是 90 是解题的关键 17 【分析】根据已知可求得菱形的边长及其两内角的度数，根据勾股定理可求得其对角线 的长，根据菱形的面积等于两对角线乘积的一半求得其面积 【解答】解：根据已知可得， 菱形的边长 ABBCCDAD10cm，ABC60，BAD120， ABC 为等边三角形， ACAB10cm，AOCO5cm， 在 RtAOB 中，根据勾股定理得：BO5， BD2BO10（cm
21、）， 则 S 菱形ABCD ACBD101050（cm2）； 故答案为：10cm，50cm2 【点评】本题考查的是菱形的面积求法及菱形性质的综合菱形的面积有两种求法（1） 利用底乘以相应底上的高（2）利用菱形的特殊性，菱形面积两条对角线的乘积 18 【分析】恒星的面积边长为 4 的正方形面积半径为 2 的圆的面积，依此列式计算即 可 【解答】解：如图 2+24， 恒星的面积444164 故答案为 164 【点评】本题考查了扇形面积的计算，关键是理解恒星的面积边长为 4 的正方形面积 半径为 2 的圆的面积 19【分析】原式提取公因式，再利用平方差公式分解即可 【解答】解：原式y（x23）y（x
22、+）（x）， 故答案为：y（x+）（x） 【点评】此题考查了实数范围内分解因式，熟练掌握因式分解的方法是解本题的关键 20【分析】根据已知可求得BEC 的度数，根据三角形外角定理可求得AGD 的度数 【解答】解：四边形 ABCD 是正方形， ABBCADCD，ABC90，ADGCDG，ABD45， GDGD， ADGCDG， AGDCGD， CGDEGB， AGDEGB， ABE 是等边三角形， ABBE，ABE60， BEBC，EBC150， BECECB15， BGE180BECEBG18015604560， AGD60 故答案为 60 【点评】本题考查等边三角形的性质及正方形的性质的运用
23、 三解答题（共三解答题（共 11 小题，满分小题，满分 90 分）分） 21【分析】将特殊锐角的三角函数值代入、计算零指数幂，再计算乘法，最后计算加减可 得 【解答】解：原式 【点评】本题主要考查实数的运算，解题的关键是熟记特殊锐角的三角函数值，掌握零 指数幂的规定及实数的运算顺序 22【分析】（1）计算判别式得到m2+12，由于 m20，则0，然后根据判别式的 意义判断根的情况； （2）设方程另一根为 x2，根据根与系数的关系先利用两根之积求出 x2，然后利用两根之 和求出 m 【解答】解：（1）m241（3）m2+12， m20， 0， 方程有两个不相等的实根； （2）设方程另一根为 x2
24、， 1x23，解得 x23， 1+3m， m2 【点评】本题考查了一元二次方程 ax2+bx+c0（a0）的根的判别式b24ac：当 0，方程有两个不相等的实数根；当0，方程有两个相等的实数根；当0，方 程没有实数根 23【分析】先根据分式的混合运算顺序和运算法则化简原式，再选取使分式有意义的 x 的值代入计算可得 【解答】解：原式 ， x1 且 x0， 在1x2 中符合条件的 x 的值为 x2， 则原式2 【点评】本题主要考查分式的化简求值，解题的关键是熟练掌握分式的混合运算顺序和 运算法则 24【分析】根据平行四边形的性质和已知条件易证EBC 是等腰三角形，由等腰三角形 的性质：三线合一即
25、可证明 CHEH 【解答】证明：在ABCD 中，BECD， E2， CE 平分BCD， 12， 1E， BEBC， 又BHBC， CHEH（三线合一） 【点评】 本题考查了平行四边形的性质、 角平分线的定义以及等腰三角形的判定和性质， 证题的关键是得到EBC 是等腰三角形 25【分析】（1）由良有 70 天，占 70%，即可求得统计图共统计了几天的空气质量情况； （2）由条形统计图中，可得空气质量为“良”的天数为 10020%20（天），空气质 量为“优”所在扇形的圆心角度数是：20%36072， （3）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与恰好选到一名男 同学和一名女同学
26、的情况，再利用概率公式即可求得答案 【解答】解：（1）良有 70 天，占 70%， 统计图共统计了的空气质量情况的天数为：7070%100（天）； （2）如图：条形统计图中，空气质量为“优”的天数为 10020%20（天）， 空气质量为“优”所在扇形的圆心角度数是：20%36072， （3）画树状图得： 共有 12 种等可能情况，其中符合一男一女的有 8 种， 恰好选到一名男同学和一名女同学的概率是 故答案为：（1）100，（2）72，（3） 【点评】本题考查的是用列表法或画树状图法求概率以及扇形统计图与条形统计图的知 识列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步
27、 完成的事件，树状图法适合两步或两步以上完成的事件用到的知识点为：概率所求 情况数与总情况数之比 26【分析】（1）分别作出点 A 和点 B 绕点 O 逆时针旋转 90所得对应点，再与点 O 首 尾顺次连接即可得； （2）由所得图形可得点的坐标； （3）利用勾股定理可得答案 【解答】解：（1）画出A1OB1，如图 （2）点 A1（0，1），点 B1（2，2） （3）OB1OB 2 【点评】本题主要考查作图旋转变换，解题的关键是掌握旋转变换的定义和性质，并 据此得出变换后的对应点 27 【分析】 （1） 设调价百分率为 x，根据售价从原来每件 40 元经两次调价后调至每件 32.4 元，可列方程
28、求解 （2）根据的条件从而求出多售的件数，从而得到两次调价后，每月可销售该商品数量 【解答】解：（1）设这种商品平均降价率是 x，依题意得： 40（1x）232.4， 解得：x10.110%，x21.9（舍去）； 故这个降价率为 10%； （2）设降价 y 元， 根据题意得（4020y）（500+50y）10000 解得：y0（舍去）或 y10， 答：在现价的基础上，再降低 10 元 【点评】考查一元二次方程的应用；求平均变化率的方法为：若设变化前的量为 a，变化 后的量为 b，平均变化率为 x，则经过两次变化后的数量关系为 a（1x）2b 28 【分析】 （1） 连接 OC 根据等腰三角形的
29、性质得到OACOCA OACCAD 推 出 OCAE根据平行线的性质得到EOCP根据切线的性质即可得到结论； （2）解直角三角形即可得到结论 【解答】解：（1）连接 OC OAOC， OACOCA BCCD， OACCAD OCACAD， OCAE EOCP PE 是的切线，C 为切点， OCP90 E90； （2）在 RtABD 中，OC2.5，sinP， OP， 在 RtAPE 中，AP+2.5，sinP， AE4 【点评】本题考查了切线的性质，解直角三角形，正确的作出辅助线是解题的关键 29【分析】（1）根据反比例函数的特点 kxy 为定值，列出方程，求出 m 的值，便可求 出反比例函数
30、的解析式；根据 m 的值求出 A、B 两点的坐标，用待定实数法便可求出一 次函数的解析式 （2）根据函数图象可直接解答 【解答】解：（1）由题意可知，m（m+1）（m+3）（m1） 解，得 m3（2 分） A（3，4），B（6，2）； k4312， A 点坐标为（3，4），B 点坐标为（6，2）， ， ， yx+6（5 分） （2）根据图象得 x 的取值范围：0x3 或 x6（7 分） 【点评】此题考查的是反比例函数图象上点的坐标特点及用待定系数法求一次函数及反 比例函数的解析式，比较简单 30【分析】根据 CE 和 的正切值可以求得 AE 的长度，根据 ABAE+EB 即可求得 AB 的长度
31、，即可解题 【解答】解：在中 RtACE， AECEtan， BDtan， 25tan22， 10.10 米， ABAE+EBAE+CD10.10+1.2011.3（米） 答：电线杆的高度约为 11.3 米 【点评】 本题考查了三角函数在直角三角形中的运用， 本题中正确计算 AE 的值是解题的 关键 31【分析】（1）变形为不定方程 k（x4）y4，然后根据 k 为任意不为 0 的实数得到 x40，y40，然后求出 x、y 即可得到定点的坐标； （2）通过解方程组得 A（6，3）、B（4，8）； 如图 1，作 PQy 轴，交 AB 于点 Q，设 P（x， x2x），则 Q（x， x+6）， 则
32、 PQ （x+6） （x2x） ， 利用三角形面积公式得到 SPAB （x1） 2+ 20，然后解方程求出 x 即可得到点 P 的坐标； 设 P（x， x2x），如图 2，利用勾股定理的逆定理证明AOB90，根据三角 形相似的判定，由于AOBPCO，则当时，CPOOAB，即 ；当时，CPOOBA，即，然后分别解关于 x 的绝对值方程即可得到对应的点 P 的坐标 【解答】解：（1）ykx4k+4k（x4）+4， 即 k（x4）y4， 而 k 为任意不为 0 的实数， x40，y40，解得 x4，y4， 直线过定点（4，4）； （2）当 k时，直线解析式为 yx+6， 解方程组得或，则 A（6，3
33、）、B（4，8）； 如图 1，作 PQy 轴，交 AB 于点 Q， 设 P（x， x2x），则 Q（x， x+6）， PQ（x+6）（x2x）（x1）2+， SPAB （6+4）PQ（x1）2+20， 解得 x12，x24， 点 P 的坐标为（4，0）或（2，3）； 设 P（x， x2x），如图 2， 由题意得：AO3，BO4，AB5， AB2AO2+BO2， AOB90， AOBPCO， 当时，CPOOAB， 即， 整理得 4|x2x|3|x|， 解方程 4（x2x）3x 得 x10（舍去），x27，此时 P 点坐标为（7，）； 解方程 4（x2x）3x 得 x10（舍去），x21，此时 P 点坐标为（1，）； 当时，CPOOBA， 即， 整理得 3|x2x|4|x|， 解方程 3（x2x）4x 得 x10（舍去），x2，此时 P 点坐标为（，）； 解方程 3（x2x）4x 得 x10（舍去），x2，此时 P 点坐标为（，） 综上所述，点 P 的坐标为：（7，）或（1，）或（，）或（，） 【点评】本题考查了二次函数综合题：熟练掌握二次函数图象上点的坐标特征和相似三 角形的判定方法；会利用待定系数法求抛物线解析式，通过解方程组求两函数图象的交 点坐标，会解一元二次方程；理解坐标与图形性质；会运用分类讨论的思想解决思想问 题
