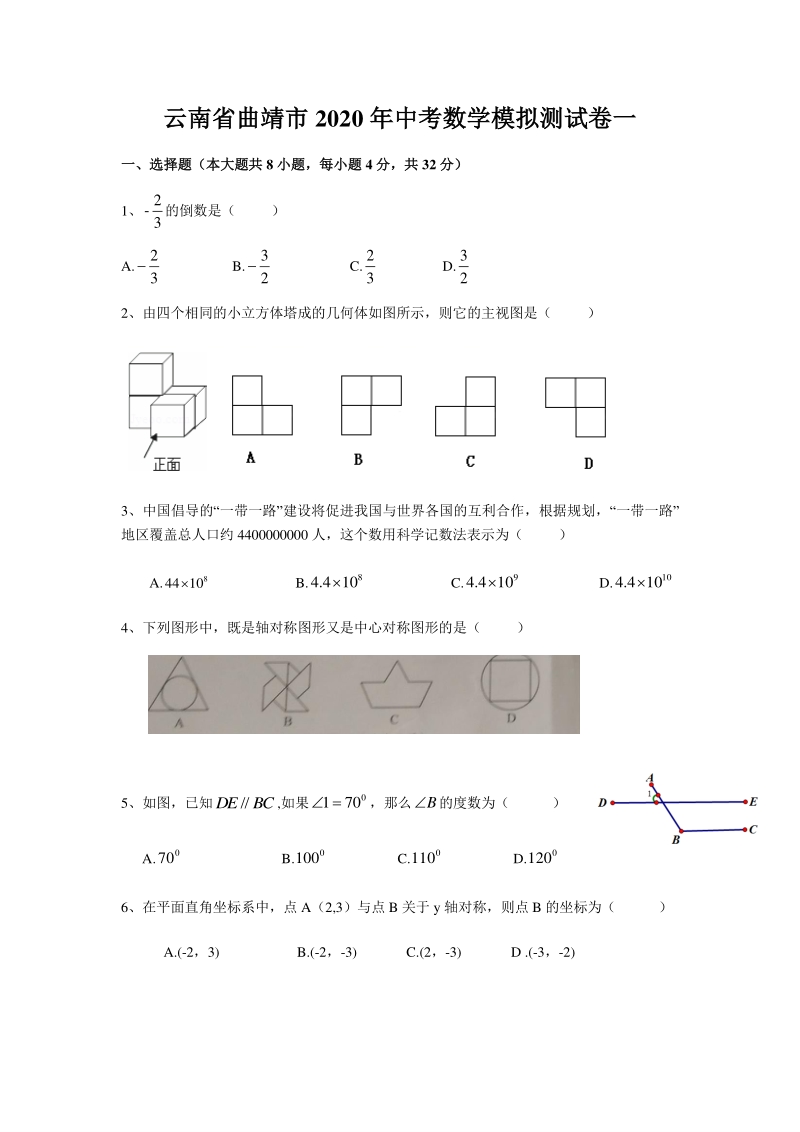
1、云南省云南省曲靖市曲靖市 2020 年中考数学年中考数学模拟测模拟测试卷试卷一一 一、一、选择题（本大题共选择题（本大题共 8 小题，每小题小题，每小题 4 分，共分，共 32 分分） 1、 3 2 -的倒数是（ ） A. 3 2 B. 2 3 C. 3 2 D. 2 3 2、由四个相同的小立方体塔成的几何体如图所示，则它的主视图是（ ） 3、中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路” 地区覆盖总人口约 4400000000 人，这个数用科学记数法表示为（ ） A. 8 1044 B. 8 104 . 4 C. 9 104 . 4 D. 10 104 .
2、4 4、下列图形中，既是轴对称图形又是中心对称图形的是（ ） 5、如图，已知BCDE/,如果 0 701，那么B的度数为（ ） A. 0 70 B. 0 100 C. 0 110 D. 0 120 6、在平面直角坐标系中，点 A（2,3）与点 B 关于 y 轴对称，则点 B 的坐标为（ ） A.(-2，3) B.(-2，-3) C.(2，-3) D .(-3，-2) 7、若4x是分式方程 3 12 xx a 的根，则a的值为( ) A.6 B.-6 C.4 D.-4 8、 如图， 在O中， 直径CD弦AB,则下列结论正确得是 （ ） A.ABAC B.BODC 2 1 C.BC D. BODA
3、 二、填空题（本大题共二、填空题（本大题共 6 小题，每小题小题，每小题 3 分，共分，共 18 分分） 9、已知3x，则x的值为 。 10、已知mnnm3，则 nm 11 的值为 。 11、直线上依次有 A,B,C,D 四个点，AD=7，AB=2，若 AB,BC,CD 可构成以 BC 为腰的等 腰三角形，则 BC 的长为 。 12、如图，如图，在 RtABC 中，ACB=90，点 D、点 E 分别是边 AB、AC 的 中点，点 F 在 AB 上，且 EFCD若 EF=2，则 AB= 。 （第 12 题图） （第 14 题图） 13、函数 y=+中自变量 x 的取值范围是 。 14、 如图，
4、在菱形ABCD中， 对角线AC与BD相交于点O,8AC,6BD,ADOE 于点E,交BC于点F,则EF的长为 。 三、解答题三、解答题（本大题共（本大题共 9 小题小题，共，共 70 分）分） 15、 （本小题满分 5 分）计算：+（） 1+|1 |4sin45 16、 （本小题满分 6 分）已知在 ABCD 中,F 是 BC 边的中点,连接 DF 并延长,交 AB 的延长 线于点 E.求证:AB=BE. 17、 （本小题满分 7 分） 某小区为了安全起见，决定将小区内的滑滑板的倾斜角由 0 45调为 0 30，如图，已知原滑滑板 AB 的长为 4 米，点 D，B,C 在同一水平地面上，调整后
5、滑滑板 会加长多少米？ （结果精确到 0.01 米， 参考数据：414. 12 ，732. 13 ，449. 26 ） 18、 （本小题满分 8 分）某区域为响应“绿水青山就是金山银山”的号召，加强了绿化建设.为 了解该区域群众对绿化建设的满意程度， 某中学数学兴趣小组在该区域的甲、 乙两个片区进 行了调查，得到如下不完整统计图。 请结合图中信息，解决下列问题： （1）此次调查中接受调查的人数为 人，其中“非常满意”的人数为 人； （2）兴趣小组准备从“不满意”的 4 位群众中随机选择 2 位进行回访，已知这 4 位群众中有 2 位来自甲片区，另 2 位来自乙片区，请用画树状图或列表的方法求出
6、选择的群众来自甲片 区的概率。 19、 （本小题满分 7 分）如图，已知一次函数bkxy的图象与反比例函数 x y 8 的图象 交于 A,B 两点，点 A 的横坐标是 2，点 B 的纵坐标是-2。 （1）求一次函数的解析式； （2）求AOB的面积。 20、 （本小题满分 8 分） 如图，AD是ABC的外接圆O的直径，点 P 在 BC 延长线上，且满足BPAC. (1)求证：PA 是O的切线； （2）弦ADCE 交AB于点 F，若12 ABAF,求 AC 的长。 21、（本题满分 8 分） 某商场将每件进价为 80 元的 A 商品按每件 100 元出售,一天可售出 128 件.经过市场调查,发现
7、这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降 价 x 元,商场一天可通过 A 商品获利润 y 元. （1）求 y 与 x 之间的函数解析式（不必写出自变量 x 的取值范围） （2）A 商品销售单价为多少时,该商场每天通过 A 商品所获的利润最大？ 22、 （本题满分 9 分）如图，ABC中，AB=AC, 0 90= BAC,点 D，E 分别在 AB,BC 上， EDAEAD=,点 F 为 DE 的延长线与 AC 的延长线的交点. （1）求证：DE=EF； （2）判断 BD 和 CF 的数量关系，并说明理由； （3）若3=AB,5=AE,求 BD 的长。 23、 （本题满分 12 分）如图，已知二次函数3 2 +=bxaxy的图象与x轴分别交于 A(1,0),B(3,0)两点，与y轴交于点 C. （1）求此二次函数解析式； （2）点 D 为抛物线的顶点，试判断BCD的形状，并说明理由； （3）将直线 BC 向上平移)0(tt个单位，平移后的直线与抛物线交于 M，N 两点（点 M 在 y 轴的右侧） ，当AMN为直角三角形时，求 t 的值
