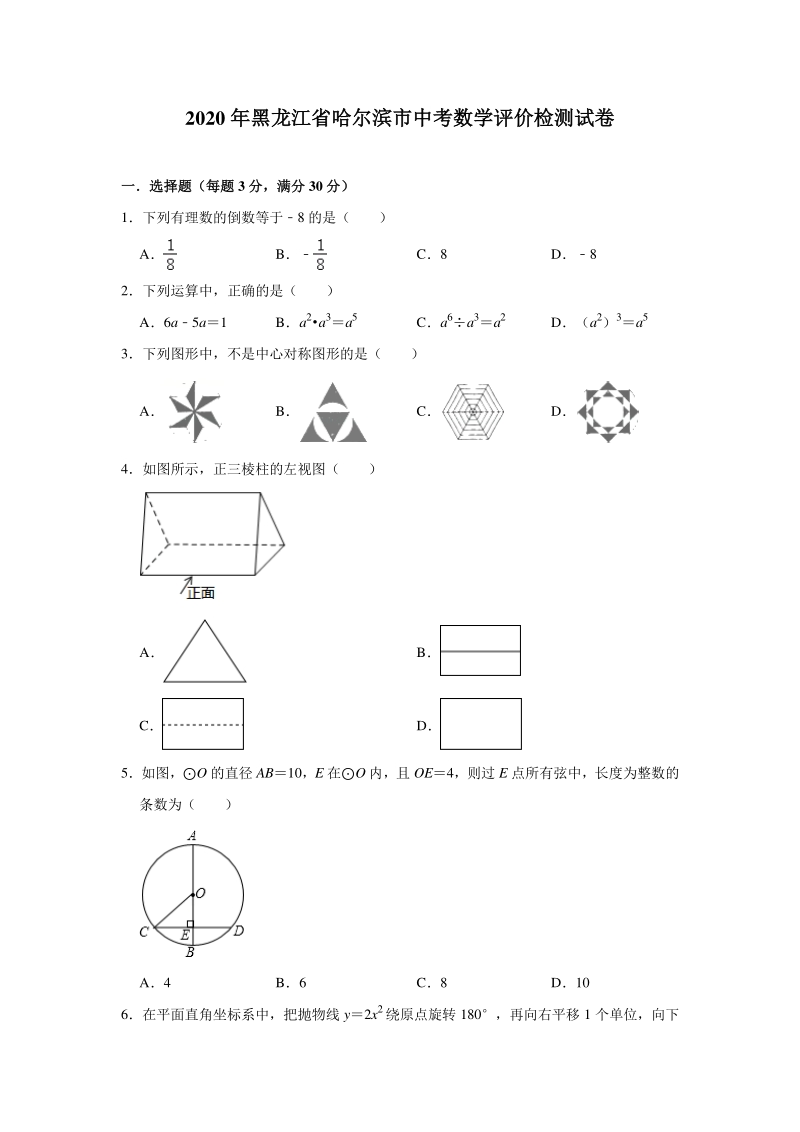
1、2020 年黑龙江省哈尔滨市中考数学评价检测试卷年黑龙江省哈尔滨市中考数学评价检测试卷 一选择题（一选择题（每题每题 3 分分，满分，满分 30 分）分） 1下列有理数的倒数等于8 的是（ ） A B C8 D8 2下列运算中，正确的是（ ） A6a5a1 Ba2 a 3a5 Ca6a3a2 D（a2）3a5 3下列图形中，不是中心对称图形的是（ ） A B C D 4如图所示，正三棱柱的左视图（ ） A B C D 5如图，O 的直径 AB10，E 在O 内，且 OE4，则过 E 点所有弦中，长度为整数的 条数为（ ） A4 B6 C8 D10 6在平面直角坐标系中，把抛物线 y2x2绕原点
2、旋转 180，再向右平移 1 个单位，向下 平移 2 个单位，所得的抛物线的函数表达式为（ ） Ay2（x1）22 By2（x+1）22 Cy2（x1）22 Dy2（x+1）22 7如图，河坝横断面的迎水坡 AB 的坡比为 3：4，BC6m，则坡面 AB 的长为（ ） A6m B8m C10m D12m 8下列函数中，y 是 x 的反比例函数的是（ ） Ay2x Byx1 Cy Dyx 9如图，矩形纸片 ABCD 中，AB4，BC8，将纸片沿 EF 折叠，使点 C 与点 A 重合， 则下列结论错误的是（ ） AABEAGF BAEAF CAEEF D 10如图，点 D 是ABC 的边 BC 上
3、一点，BADC，AC2AD，如果ACD 的面积 为 15，那么ABD 的面积为（ ） A15 B10 C7.5 D5 二填空题（满分二填空题（满分 30 分，每小题分，每小题 3 分）分） 11港珠澳大桥被英国卫报誉为“新世界七大奇迹”之一，它是世界总体跨度最长的跨 海大桥，全长 55000 米，数字 55000 用科学记数法表示为 12若代数式在实数范围内有意义，则 x 的取值范围是 13 如图， 长方形的长宽分别为 a， b， 且 a 比 b 大 5， 面积为 10， 则 a2bab2的值为 14计算： 15对于有理数 m，我们规定m表示不大于 m 的最大整数，例如1.21，33，2.5
4、3，若5，则整数 x 的取值是 16一个不透明的口袋中有四个完全相同的小球，把它们分别标号为 1、2、3、4随机摸 取一个小球然后放回，再随机摸出一个小球，两次取出的小球标号的和等于 5 的概率 是 17在半径为 3cm 的O 中，45的圆周角所对的弧长为 cm 18如图，在矩形 ABCD 中，对角线 AC 与 BD 相交于点 O，AEBD，垂足为 E，AOB 60，AC12，则 BE 的长为 19如图，PA，PB 是O 的两条切线，A，B 为切点，点 D，E，F 分别在线段 AB，BP， AP 上，且 ADBE，BDAF，P54，则EDF 度 20如图，在ABC 和ADE 中，BACDAE9
5、0，ABAC，ADAE，C，D，E 三点在同一条直线上，连接 BD，则下列结论正确的是 ABDACE ACE+DBC45 BDCE EAB+DBC180 三解答题三解答题 21（7 分）先化简，再求值：，其中 xsin45，ycos60 22 （7 分）如图，在边长为 1 个单位长度的小正方形组成的网格中，给出了格点ABC（顶 点为网格线的交点）及过格点的直线 l （1）画出ABC 关于直线 l 对称的A1B1C1； （2） 将ABC向上平移3个单位长度， 再向左平移1个单位长度， 画出平移后的A2B2C2； （3）以 A、A1、A2为顶点的三角形中，tanA2AA1 23（8 分）书籍是人类
6、进步的阶梯联合国教科文组织把每年的 4 月 23 日确定为“世界 读书日”某校为了了解该校学生一个学期阅读课外书籍的情况，在全校范围内随机对 100 名学生进行了问卷调查，根据调查的结果，绘制了统计图表的一部分： 一个学期平均一天阅读课外书籍所有时间统计表 时间 （分钟） 20 40 60 80 100 120 人数（名） 43 31 15 5 4 2 请你根据以上信息解答下列问题： （1）补全图 1、图 2； （2）这 100 名学生一个学期平均每人阅读课外书籍多少本？若该校共有 4000 名学生， 请你估计这个学校学生一个学期阅读课外书籍共多少本？ （3）根据统计表，求一个学期平均一天阅读
7、课外书籍所用时间的众数和中位数 24（8 分）在正方形 ABCD 中，点 E 是 BC 边上一点，连接 AE （1）如图 1，点 F 为 AE 的中点，连接 CF已知 tanFBE，BF5，求 CF 的长； （2）如图 2，过点 E 作 AE 的垂线交 CD 于点 G，交 AB 的延长线于点 H，点 O 为对角 线 AC 的中点，连接 GO 并延长交 AB 于点 M，求证：AM+BHBE 25（10 分）倡导健康生活推进全民健身，某社区去年购进 A，B 两种健身器材若干件，经 了解，B 种健身器材的单价是 A 种健身器材的 1.5 倍，用 7200 元购买 A 种健身器材比用 5400 元购买
8、 B 种健身器材多 10 件 （1）A，B 两种健身器材的单价分别是多少元？ （2）若今年两种健身器材的单价和去年保持不变，该社区计划再购进 A，B 两种健身器 材共 50 件，且费用不超过 21000 元，请问：A 种健身器材至少要购买多少件？ 26（10 分）已知：ABC 内接于O，连接 CO 并延长交 AB 于点 E，交O 于点 D，满 足BEC3ACD （1）如图 1，求证：ABAC； （2）如图 2，连接 BD，点 F 为弧 BD 上一点，连接 CF，弧 CF弧 BD，过点 A 作 AG CD，垂足为点 G，求证：CF+DGCG； （3）如图 3，在（2）的条件下，点 H 为 AC
9、上一点，分别连接 DH，OH，OHDH， 过点 C 作 CPAC，交O 于点 P，OH：CP1：，CF12，连接 PF，求 PF 的长 27 （10 分）如图 1：抛物线 yax2+bx+3 交 x 轴于点 A、B，连接 AC、BC，tanABC1， tanBAC3 （1）求抛物线的解析式； （2）如图 2，点 P 在第一象限的抛物线上，连接 PC、PA，若点 P 横坐标为 t，PAC 的面积为 S，求 S 与 t 的函数关系式； （3）在（2）的条件下，当 S3 时，点 G 为第二象限抛物线上一点，连接 PG，CH PG 于点 H，连接 OH，若 tanOHG，求 GH 的长 参考答案参考答
10、案 一选择题一选择题 1解：因为的倒数等于8， 所以有理数的倒数等于8 的是 故选：B 2解：A、6a5aa，故此选项错误； B、a2 a 3a5，正确； C、a6a3a3，故此选项错误； D、（a2）3a6，故此选项错误； 故选：B 3解：A、是中心对称图形，故本选项错误； B、不是中心对称图形，故本选项正确； C、是中心对称图形，故本选项错误； D、是中心对称图形，故本选项错误； 故选：B 4解：主视图是一个矩形，俯视图是两个矩形，左视图是正三角形， 故选：A 5解：AB10， OBOAOC5， 过 E 作 CDAB 于 E，连接 OC，则 CD 是过 E 的O 的最短的弦， OBCD，
11、CEO90， 由勾股定理得：CE3， OECD，OE 过 O， CD2CE6， AB 是过 E 的O 的最长弦，AB10， 过 E 点所有弦中，长度为整数的条数为 1+2+2+2+18， 故选：C 6解：把抛物线 y2x2绕原点旋转 180， 新抛物线解析式为：y2x2， 再向右平移 1 个单位，向下平移 2 个单位， 平移后抛物线的解析式为 y2（x1）22 故选：C 7解：河坝横断面的迎水坡 AB 的坡比为 3：4，BC6m， ， 即， 解得：AC8 故 AB10（m） 故选：C 8解：A、y2x 是正比例函数，故本选项不符合题意 B、y 是 x 的反比例函数，故本选项符合题意； C、y
12、不是 x 的反比例函数，故本选项不符合题意； D、yx 是正比例函数，故本选项不符合题意； 故选：B 9解：设 BEx，则 CEBCBE8x， 沿 EF 翻折后点 C 与点 A 重合， AECE8x， 在 RtABE 中，AB2+BE2AE2， 即 42+x2（8x）2 解得 x3， AE835， 由翻折的性质得，AEFCEF， 矩形 ABCD 的对边 ADBC， AFECEF， AEFAFE， AEAF5， B 结论正确； 在 RtABE 和 RtAGF 中， ， RtABERtAGF（HL）， A 结论正确； 过点 E 作 EHAD 于 H，则四边形 ABEH 是矩形， EHAB4， AH
13、BE3， FHAFAH532， 在 RtEFH 中，EF2， D 结论正确； AEF 不是等边三角形， EFAF， C 结论错误 故选：C 10解：BADC，BB， BADBCA， AC2AD， （）2， ， ACD 的面积为 15， ABD 的面积155， 故选：D 二填空题二填空题 11解：数字 55000 用科学记数法表示为 5.5104 故答案为：5.5104 12解：根据题意得：32x0，解得：x 13解：长方形的长宽分别为 a，b，且 a 比 b 大 5，面积为 10， ab5，ab10， 则 a2bab2ab（ab） 510 50 故答案为：50 14解：原式23 6 故答案为：
14、6 15解：m表示不大于 m 的最大整数， 54， 解得：17x14， 整数 x 为17，16，15， 故答案为17，16，15 16解：画树状图如下： 随机地摸出一个小球，然后放回，再随机地摸出一个小球，共有 16 种等可能的结果数， 其中两次摸出的小球标号的和等于 5 的占 4 种， 所有两次摸出的小球标号的和等于 5 的概率为， 故答案为： 17解：根据圆周角定理，得弧所对的圆心角是 90， 根据弧长的公式 lcm， 故答案为： 18解：在矩形 ABCD 中，对角线 AC 与 BD 相交于点 O， ACBD12，OAAC6，OBBD， OAOB6， AOB60， ABO 是等边三角形，
15、AEBD， BEOB3； 故答案为：3 19解：PA，PB 是O 的两条切线， PAPB， PABPBA63， 在AFD 和BDE 中， ， AFDBDE（SAS） AFDBDE， EDF180BDEADF180AFDADFFAD63， 故答案为：63 20解：BACDAE90， BAC+CADDAE+CAD，即BADCAE， 在BAD 和CAE 中， ， BADCAE（SAS），故符合题意， BDCE， ABC 为等腰直角三角形， ABCACB45， ABD+DBC45， BADCAE， ABDACE， ACE+DBC45，故符合题意， ABD+DBC45， ACE+DBC45， DBC+D
16、CBDBC+ACE+ACB90， 则 BDCE，故符合题意， BAC+DAE+BAE+DAC360， BAE+DAC180， BDCE，ADE45， ADB45ACB， DACCBD， BAE+DBC180，故符合题意， 故答案为： 三解答三解答 21解：原式 ， 当 xsin45，ycos60时， 原式 22解：（1）如图所示，A1B1C1即为所求； （2）如图所示，A2B2C2即为所求； （3）如图， A2 A ，A2A1 ， A2A1A2A， 设 AA1交直线 l 于点 O， A1 O ， A1OAO， A2OAA1， tanA2AA12， 故答案为：2 23 解：（1）根据题意得：10
17、0（9+38+25+11+9+3）5（人）；1（35%+25%+6%） 34%， 补全图形，如图所示； （2）根据题意得：3（本）， 则这 100 名学生一个学期平均每人阅读课外书籍 3 本； 根据题意得：3400012000（本）， 则估计这个学校学生一个学期阅读课外书籍共 12000 本； （3）根据表格得：众数为 20 分钟，中位数为 40 分钟 24解：（1）RtABE 中，BF 为中线，BF5， AE10，FE5， 作 FPBC 于点 P， RtBFP 中， BP3，FP4， 在等腰三角形BFE 中，BE2BP6， 由勾股定理求得， CP835， ； （2）ACDBAC45，AOCO
18、，AOMCOG， 证明AMOCGO（ASA）， AMGC， 过 G 作 GP 垂直 AB 于点 P，得矩形 BCGP， CGPB， ABPG，AEBH，ABEGPH， ABEGPH（ASA）， BEPHPB+BHCG+BHAM+BH 25解：（1）设 A 种型号健身器材的单价为 x 元/套，B 种型号健身器材的单价为 1.5x 元/ 套， 根据题意，可得：， 解得：x360， 经检验 x360 是原方程的根， 1.5360540（元）， 因此，A，B 两种健身器材的单价分别是 360 元，540 元； （2）设购买 A 种型号健身器材 m 套，则购买 B 种型号的健身器材（50m）套， 根据题
19、意，可得：360m+540（50m）21000， 解得：m33， 因此，A 种型号健身器材至少购买 34 套 26（1）证明：如图 1 中，连接 AD设BEC3，ACD BECBAC+ACD， BAC2， CD 是直径， DAC90， D90， BD90， ACB180BACABC1802（90）90 ABCACB， ABAC （2）证明：如图 2 中，连接 AD，在 CD 上取一点 Z，使得 CZBD ， DBCF， DBADCA，CZBD，ABAC， ADBAZC（SAS）， ADAZ， AGDZ， DGGZ， CGCZ+GZBD+DGCF+DG （3）解：连接 AD，PA，作 OKAC
20、于 K，ORPC 于 R，CTFP 交 FP 的延长线于 T CPAC， ACP90， PA 是直径， ORPC，OKAC， PRRC，ORCOKCACP90， 四边形 OKCR 是矩形， RCOK， OH：PC1：， 可以假设 OHa，PC2a， PRRCa， RCOKa，sinOHK， OHK45， OHDH， DHO90， DHA180904545， CD 是直径， DAC90， ADH904545， DHAADH， ADAH， COPAOD， ADPC， AHADPC2a， AKAH+HK2a+a3a， 在 RtAOK 中，tanOAK，OAa， sinOAK， ADG+DAG90，A
21、CD+ADG90， DAGACD， AOCO， OAKACO， DAGACOOAK， tanACDtanDAGtanOAK， AG3DG，CG3AG， CG9DG， 由（2）可知，CGDG+CF， DG+129DG， DG，AG3DG3， AD， PCAD， sinFsinOAK， sinF， CTFC12，FT ，PT， PFFTPT 27解：（1）c3，故 OC3，tanABC1，则 OA3， tanBAC3，则 OA1， 故点 A、B、C 的坐标分别为：（1，0）、（3，0）、（0，3）， 则抛物线的表达式为：ya（x+1）（x3）， 将点 C 坐标代入上式并解得：a1， 故抛物线的表达
22、式为：yx2+2x+3； （2）点 P（t，t2+2t+3），点 A（1，0）， 将点 P、A 坐标代入一次函数表达式 ykx+b 并解得： 直线 PA 的表达式为：y（3t）（x+1）， 设直线 AP 交 y 轴于点 R，则 R（0，3t）， SCR（xP xA） （33+t）（t+1）t2+t； （3）St2+t3，解得：t3（舍去）或 2， 故点 P（2，3），而点 C（0，3）， 连接 CP，则 CPx 轴， CHGP，则CPHOCH， HMCP，则CHMHCO， 过点 O 作 ONCH 交 CH 的延长线于点 N，作 HMCP 于点 M， CP2，OC3， CHCPsin2sin，ONOCsin3sin，CNOCcos3cos， ONCN，GHCH， HONOHG， 故 tanHONtanOHG， 解得：tan，则 sin ，cos， MHCHcos2sincos，CMCHsin，故点 H（，）； 设点 G（m，m2+2m+3），而点 P（2，3）， 由点 G、P 的坐标得，直线 PG 表达式中的 k 值为：mtan， 故点 G（，）， 由点 G、H 的坐标得，GH
