 数学(理科)高三二轮复习系列专题3 规范答题示例3
数学(理科)高三二轮复习系列专题3 规范答题示例3
《数学(理科)高三二轮复习系列专题3 规范答题示例3》由会员分享,可在线阅读,更多相关《数学(理科)高三二轮复习系列专题3 规范答题示例3(14页珍藏版)》请在七七文库上搜索。
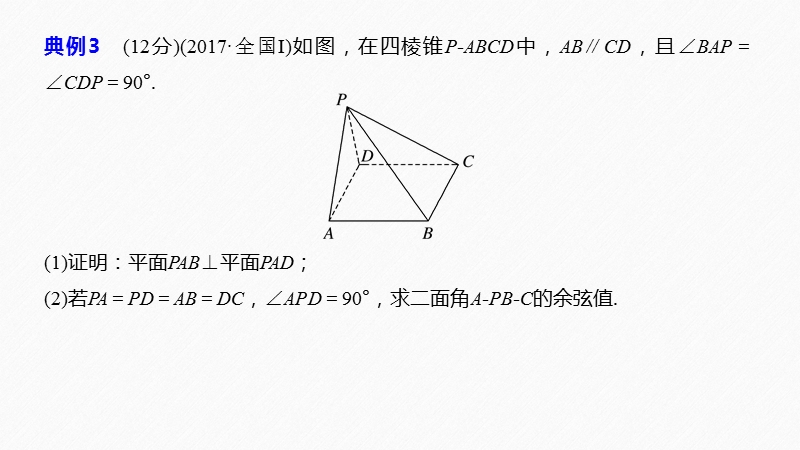
1、,立体几何与空间向量,板块二 专题三 规范答题示例3,典例3 (12分)(2017全国)如图,在四棱锥P-ABCD中,ABCD,且BAPCDP90. (1)证明:平面PAB平面PAD; (2)若PAPDABDC,APD90,求二面角A-PB-C的余弦值.,审题路线图,计算平面PCB与平面PAB的法向量计算两个法向量的夹角的余弦值求得二面角的余弦值.,规范解答 分步得分,(1)证明 由已知BAPCDP90,得ABAP,CDPD. 由于ABCD,故ABPD, 又PDPAP,PD,PA平面PAD, 所以AB平面PAD. 2分 又AB平面PAB,3分 所以平面PAB平面PAD.4分,(2)解 在平面P
2、AD内作PFAD, 垂足为点F,由(1)知,AB平面PAD, 故ABPF,可得PF平面ABCD.,设n(x,y,z)是平面PCB的法向量,,设m(x,y,z)是平面PAB的法向量,,由图知二面角APBC为钝二面角,,构建答题模板,第一步 找垂直:找出(或作出)具有公共交点的两条直线,寻求与它们有垂直关系 的直线,由线面垂直得出面面垂直. 第二步 写坐标:选择恰当的坐标原点,建立空间直角坐标系,写出点坐标. 第三步 求向量:求两个平面的法向量. 第四步 求夹角:运用夹角的余弦公式代入数值,计算向量的夹角. 第五步 得结论:得到要求两个平面所成的角.,评分细则 第(1)问:证得AB平面PAD得2分
3、,直接写出不得分;写出AB平面PAB得1分,此步没有扣1分;写出结论平面PAB平面PAD得1分. 第(2)问:正确建立空间直角坐标系得2分;写出相应的坐标及向量得1分(酌情);正确求出平面PCB的法向量得1分;正确求出平面PAB的法向量得1分;写出公式cosn,m 得1分,正确求出值再得1分;写出正确结果得1分.,跟踪演练3 (2018全国)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把DFC折起,使点C到达点P的位置,且PFBF. (1)证明:平面PEF平面ABFD;,证明 由已知可得BFPF,BFEF, PFEFF,PF,EF平面PEF, 所以BF平面PEF. 又BF平面ABFD, 所以平面PEF平面ABFD.,(2)求DP与平面ABFD所成角的正弦值.,解 如图,作PHEF,垂足为H. 由(1)得,PH平面ABFD.,建立如图所示的空间直角坐标系Hxyz. 由(1)可得,DEPE.,又PF1,EF2,所以PEPF.,设DP与平面ABFD所成的角为,,本课结束,


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 数学理科高三二轮复习系列专题3 规范答题示例3 数学 理科 二轮 复习 系列 专题 规范 答题 示例
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-131345.html