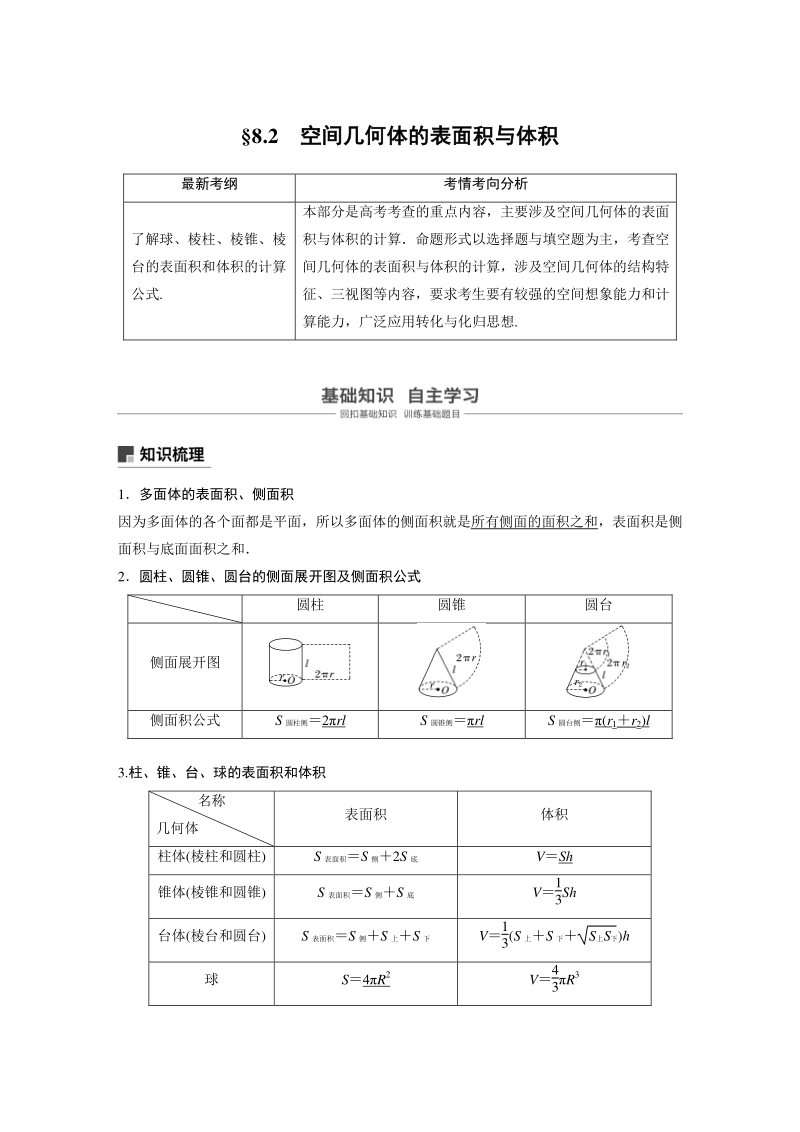
1、 8.2 空间几何体的表面积与体积空间几何体的表面积与体积 最新考纲 考情考向分析 了解球、棱柱、棱锥、棱 台的表面积和体积的计算 公式. 本部分是高考考查的重点内容，主要涉及空间几何体的表面 积与体积的计算命题形式以选择题与填空题为主，考查空 间几何体的表面积与体积的计算，涉及空间几何体的结构特 征、三视图等内容，要求考生要有较强的空间想象能力和计 算能力，广泛应用转化与化归思想. 1多面体的表面积、侧面积 因为多面体的各个面都是平面，所以多面体的侧面积就是所有侧面的面积之和，表面积是侧 面积与底面面积之和 2圆柱、圆锥、圆台的侧面展开图及侧面积公式 圆柱 圆锥 圆台 侧面展开图 侧面积公式
2、 S圆柱侧2rl S圆锥侧rl S圆台侧(r1r2)l 3.柱、锥、台、球的表面积和体积 名称 几何体 表面积 体积 柱体(棱柱和圆柱) S表面积S侧2S底 VSh 锥体(棱锥和圆锥) S表面积S侧S底 V1 3Sh 台体(棱台和圆台) S表面积S侧S上S下 V1 3(S 上S下 S上S下)h 球 S4R2 V4 3R 3 知识拓展 1与体积有关的几个结论 (1)一个组合体的体积等于它的各部分体积的和或差 (2)底面面积及高都相等的两个同类几何体的体积相等 2几个与球有关的切、接常用结论 (1)正方体的棱长为 a，球的半径为 R， 若球为正方体的外接球，则 2R 3a； 若球为正方体的内切球，
3、则 2Ra； 若球与正方体的各棱相切，则 2R 2a. (2)若长方体的同一顶点的三条棱长分别为 a，b，c，外接球的半径为 R，则 2Ra2b2c2. (3)正四面体的外接球与内切球的半径之比为 31. 题组一 思考辨析 1判断下列结论是否正确(请在括号中打“”或“”) (1)多面体的表面积等于各个面的面积之和( ) (2)锥体的体积等于底面积与高之积( ) (3)球的体积之比等于半径比的平方( ) (4)简单组合体的体积等于组成它的简单几何体体积的和或差( ) (5)长方体既有外接球又有内切球( ) (6)圆柱的一个底面积为 S， 侧面展开图是一个正方形， 那么这个圆柱的侧面积是 2S.(
4、 ) 题组二 教材改编 2P27T1已知圆锥的表面积等于12 cm2，其侧面展开图是一个半圆，则底面圆的半径为( ) A1 cm B2 cm C3 cm D.3 2 cm 答案 B 解析 S表r2rlr2r 2r3r212， r24，r2. 3P28A 组 T3如图，将一个长方体用过相邻三条棱的中点的平面截出一个棱锥，则该棱锥 的体积与剩下的几何体体积的比为_ 答案 147 解析 设长方体的相邻三条棱长分别为 a，b，c，它截出棱锥的体积 V11 3 1 2 1 2a 1 2b 1 2c 1 48abc，剩下的几何体的体积 V2abc 1 48abc 47 48abc，所以 V1V2147.
5、题组三 易错自纠 4(2017 西安一中月考)一个几何体的三视图如图所示，则该几何体的表面积为( ) A3 B4 C24 D34 答案 D 解析 由几何体的三视图可知， 该几何体为半圆柱， 直观图如图所示 表面积为 2221 21 21243. 5(2016 全国)体积为 8 的正方体的顶点都在同一球面上，则该球的表面积为( ) A12 B.32 3 C8 D4 答案 A 解析 由题意可知正方体的棱长为 2， 其体对角线 2 3即为球的直径， 所以球的表面积为 4R2 (2R)212，故选 A. 6 (2018 大连调研)如图为一个半球挖去一个圆锥后的几何体的三视图， 则剩余部分与挖去部 分的
6、体积之比为_ 答案 11 解析 由三视图可知半球的半径为 2，圆锥底面圆的半径为 2，高为 2，所以 V圆锥1 32 3 8 3，V 半球1 2 4 32 316 3 ，所以 V剩余V半球V圆锥8 3，故剩余部分与挖去部分的体积 之比为 11. 题型一 求空间几何体的表面积 1 (2016 全国)如图， 某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半 径若该几何体的体积是28 3 ，则它的表面积是( ) A17 B18 C20 D28 答案 A 解析 由题意知，该几何体的直观图如图所示，它是一个球(被过球心 O 且 互相垂直的三个平面)切掉左上角的1 8后得到的组合体，其表面积是
7、球面面积 的7 8和三个 1 4圆面积之和 由4 3R 31 8 4 3R 328 3 ，得球的半径 R2. 则得 S7 842 231 42 217，故选 A. 2 (2017 黑龙江哈师大附中一模)已知某几何体的三视图如图所示， 则该几何体的表面积为( ) A.7 3 B.17 2 C13 D.173 10 2 答案 C 解析 由三视图可知几何体为三棱台， 作出直观图如图所示 则 CC 平面 ABC， 上、 下底均为等腰直角三角形， ACBC， ACBC1， AC BCCC2， AB 2，AB2 2. 棱台的上底面面积为1 211 1 2，下底面面积为 1 2222，梯形 ACCA的面积为
8、1 2(12)23，梯形 BCCB的面积为 1 2(12)23，过 A 作 ADAC于点 D，过 D 作 DEAB，则 ADCC2， DE 为ABC斜边高的1 2，DE 2 2 ， AE AD2DE2 3 2， 梯形 ABBA的面积为1 2( 22 2) 3 2 9 2， 几何体的表面积 S1 2233 9 213，故选 C. 思维升华 空间几何体表面积的求法 (1)以三视图为载体的几何体的表面积问题，关键是分析三视图确定几何体中各元素之间的位 置关系及数量 (2)多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理 (3)旋转体的表面积问题注意其侧面展开图的应用 题型二 求空间
9、几何体的体积 命题点 1 以三视图为背景的几何体的体积 典例 (2017 浙江)某几何体的三视图如图所示(单位： cm)， 则该几何体的体积(单位： cm3)是( ) A. 21 B. 23 C.3 2 1 D.3 2 3 答案 A 解析 由几何体的三视图可知，该几何体是一个底面半径为 1，高为 3 的圆锥的一半与一个 底面为直角边长是 2的等腰直角三角形，高为 3 的三棱锥的组合体， 该几何体体积为 V1 3 1 21 231 3 1 2 2 23 21. 命题点 2 求简单几何体的体积 典例 (2018 广州调研)已知 E，F 分别是棱长为 a 的正方体 ABCDA1B1C1D1的棱 AA
10、1，CC1 的中点，则四棱锥 C1B1EDF 的体积为_ 答案 1 6a 3 解析 方法一 如图所示，连接 A1C1，B1D1交于点 O1，连接 B1D， EF，过点 O1作 O1HB1D 于点 H. 因为 EFA1C1，且 A1C1平面 B1EDF，EF平面 B1EDF， 所以 A1C1平面 B1EDF. 所以 C1到平面 B1EDF 的距离就是 A1C1到平面 B1EDF 的距离 易知平面 B1D1D平面 B1EDF， 又平面 B1D1D平面 B1EDFB1D， 所以 O1H平面 B1EDF， 所以 O1H 等于四棱锥 C1B1EDF 的高 因为B1O1HB1DD1， 所以 O1HB1O1
11、 DD1 B1D 6 6 a. 所以 11 CB EDF V 1 31 B EDF S四边形 O1H1 3 1 2 EF B1D O1H 1 3 1 2 2a 3a 6 6 a1 6a 3. 方法二 连接 EF，B1D. 设 B1到平面 C1EF 的距离为 h1，D 到平面 C1EF 的距离为 h2，则 h1h2B1D1 2a. 由题意得， 11111 CB EDFBC EFD C EF VVV 四棱锥三棱锥三棱锥 1 3 1 C EF S (h1h2)1 6a 3. 思维升华 空间几何体体积问题的常见类型及解题策略 (1)若所给定的几何体是可直接用公式求解的柱体、 锥体或台体， 则可直接利用
12、公式进行求解 (2)若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法 进行求解 (3)若以三视图的形式给出几何体， 则应先根据三视图得到几何体的直观图， 然后根据条件求解 跟踪训练 (1)(2017 新乡二模)已知一个几何体的三视图如图所示， 则该几何体的体积为( ) A.32 3 B.16 3 C.8 3 D.4 3 答案 C 解析 该几何体由一个三棱锥和一个三棱柱组合而成，直观图如图所示， VV柱V锥1 2(11)12 1 3 1 2(11)12 8 3，故选 C. (2)如图，在多面体 ABCDEF 中，已知 ABCD 是边长为 1 的正方形，且ADE，BC
13、F 均为 正三角形，EFAB，EF2，则该多面体的体积为( ) A. 2 3 B. 3 3 C.4 3 D. 3 2 答案 A 解析 如图，分别过点 A，B 作 EF 的垂线，垂足分别为 G，H，连 接 DG，CH， 容易求得 EGHF1 2， AGGDBHHC 3 2 ， 取 AD 的中点 O，连接 GO，易得 GO 2 2 ， SAGDSBHC1 2 2 2 1 2 4 ， 多面体的体积 VV三棱锥EADGV三棱锥FBCHV三棱柱AGDBHC2V三棱锥EADGV三棱柱AGDBHC 1 3 2 4 1 22 2 4 1 2 3 .故选 A. 题型三 与球有关的切、接问题 典例 (2016 全
14、国)在封闭的直三棱柱 ABCA1B1C1内有一个体积为 V 的球若 ABBC， AB6，BC8，AA13，则 V 的最大值是( ) A4 B.9 2 C6 D.32 3 答案 B 解析 由题意知，底面三角形的内切圆直径为 4.三棱柱的高为 3，所以球的最大直径为 3，V 的最大值为9 2 . 引申探究 1若将本例中的条件变为“直三棱柱 ABCA1B1C1的 6 个顶点都在球 O 的球面上”， 若 AB 3，AC4，ABAC，AA112，求球 O 的表面积 解 将直三棱柱补形为长方体 ABECA1B1E1C1， 则球 O 是长方体 ABECA1B1E1C1的外接球 体对角线 BC1的长为球 O
15、的直径 因此 2R 324212213.故 S球4R2169. 2若将本例中的条件变为“正四棱锥的顶点都在球 O 的球面上”，若该棱锥的高为 4，底面 边长为 2，求该球的体积 解 如图，设球心为 O，半径为 r，则在 RtAOF 中， (4r)2( 2)2r2， 解得 r9 4， 则球 O 的体积 V球4 3r 34 3 9 4 3243 16 . 思维升华 空间几何体与球接、切问题的求解方法 (1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为 平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解 (2)若球面上四点 P，A，B，C 构成的
16、三条线段 PA，PB，PC 两两互相垂直，且 PAa，PB b，PCc，一般把有关元素“补形”成为一个球内接长方体，利用 4R2a2b2c2求解 跟踪训练 (2018 深圳调研)如图所示， 在平面四边形 ABCD 中， ABADCD1， BD 2， BDCD，将其沿对角线 BD 折成四面体 ABCD，使平面 ABD平面 BCD，若四面体 ABCD 的顶点在同一个球面上，则该球的体积为( ) A. 3 2 B3 C. 2 3 D2 答案 A 解析 如图， 取 BD 的中点为 E， BC 的中点为 O， 连接 AE， OD， EO， AO.因为 ABAD， 所以 AEBD. 由于平面 ABD平面
17、BCD，所以 AE平面 BCD. 因为 ABADCD1，BD 2， 所以 AE 2 2 ，EO1 2. 所以 OA 3 2 . 在 RtBDC 中，OBOCOD1 2BC 3 2 ， 所以四面体 ABCD 的外接球的球心为 O，半径为 3 2 . 所以该球的体积 V4 3 3 2 3 3 2 . 三视图(基本的、和球联系的) 考点分析 三视图是高考重点考查的一个知识点，主要考查由几何体的三视图还原几何体的 形状，进而求解表面积、体积等知识，所涉及的几何体既包括柱、锥、台、球等简单几何体， 也包括一些组合体，处理此类题目的关键是通过三视图准确还原几何体 典例 1 已知某几何体的三视图如图所示，则
18、该几何体的体积等于( ) A.160 3 B160 C6432 2 D60 解析 由题意知该几何体是由一个直三棱柱和一个四棱锥组成的组合 体，如图所示，其中直三棱柱的高为 844，故 V直三棱柱8432， 四棱锥的底面为边长为 4 的正方形，高为 4， 故 V四棱锥1 3164 64 3 ， 故该几何体的体积 VV直三棱柱V四棱锥3264 3 160 3 ，故选 A. 答案 A 典例 2 某组合体的三视图如图所示，则该组合体的体积为_ 解析 如图所示， 该组合体由一个四棱锥和四分之一个球组成， 球的半径为 1， 四棱锥的高为球的半径，四棱锥的底面为等腰梯形，上底为 2，下底为 1，高为 3 2 ，所以该组合体的体积 V1 3 1 2(21) 3 2 11 4 4 31 3 3 4 3. 答案 3 4 3
