1、第 1 页 共 10 页 中考总复习：中考总复习：二次函数二次函数巩固练习（提高巩固练习（提高） 【巩固练习巩固练习】 一、选择题一、选择题 1. 如图，两条抛物线1 2 1 2 1 xy、1 2 1 2 2 xy与分别经过点0 , 2,0 , 2且平行于y轴的两 条平行线围成的阴影部分的面积为（ ） A4 B6 C8 D10 2 反比例函数 x y 6 图象上有三个点)( 11 yx ，)( 22 yx ，)( 33 yx ， 其中 321 0xxx， 则 1 y， 2 y， 3 y的大小关系是（ ） A 321 yyy B 312 yyy C 213 yyy D 123 yyy 3函数yk
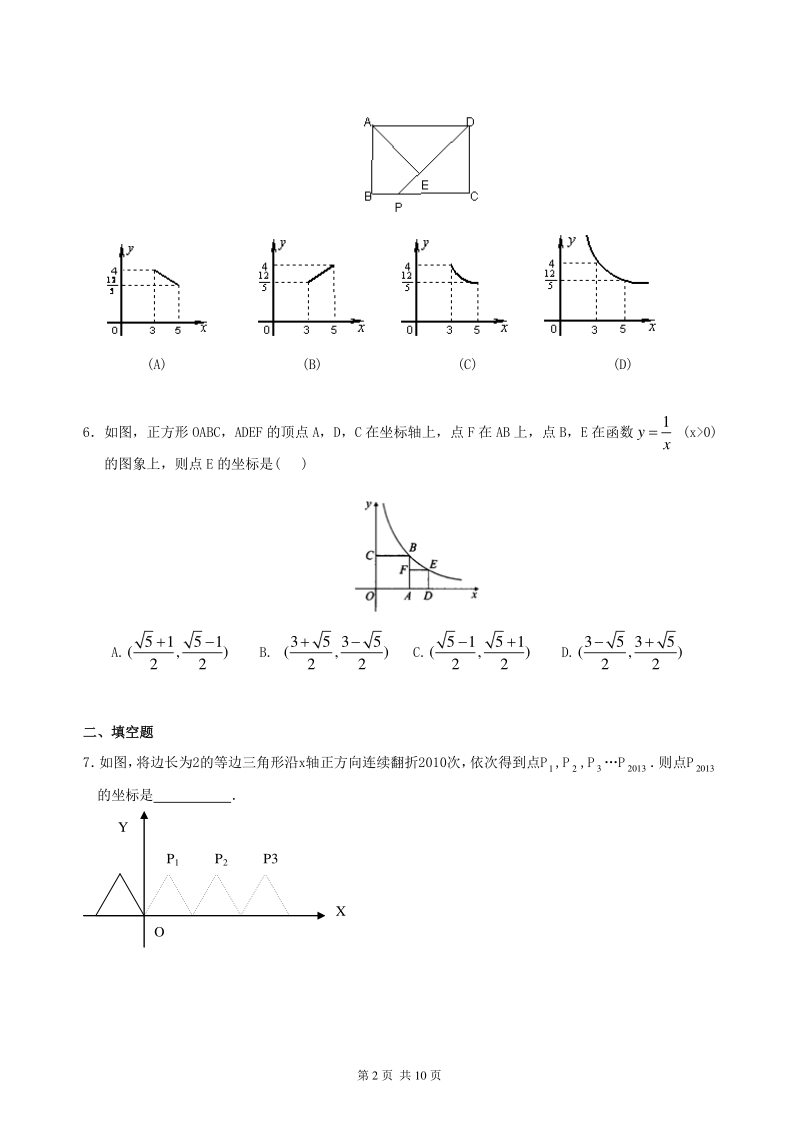
2、xk与(0) k yk x 在同一坐标系中的大致图象是（ ） 4二次函数cbxaxy 2 的图,象如图所示，那么abc、acb4 2 、ba2、cba24这四个 代数式中，值为正的有（ ） A.4 个 B.3 个 C.2 个 D.1 个 21 世纪教育网 5如图，在矩形 ABCD 中，AB=3，BC=4，点 P 在 BC 边上运动，连结 DP，过点 A 作 AEDP，垂足为 E， 设 DP=x，AE=y，则能反映 y 与 x 之间函数关系的大致图象是( ) 第 2 页 共 10 页 (A) (B) (C) (D) 6如图，正方形 OABC，ADEF 的顶点 A，D，C 在坐标轴上，点 F 在
3、AB 上，点 B，E 在函数 1 y x (x0) 的图象上，则点 E 的坐标是( ) A. 5151 (,) 22 B. 35 35 (,) 22 C. 5151 (,) 22 D. 35 35 (,) 22 二、填空题二、填空题 7 如图， 将边长为2的等边三角形沿x轴正方向连续翻折2010次， 依次得到点P1,P 2,P3P2013 则点P2013 的坐标是 P1P3P2 O Y X 第 3 页 共 10 页 8一次函数y= 3 4 x+4 分别交x轴、y轴于A、B两点，在x轴上取一点 C，使ABC为等腰三角形，则这 样的的点 C 最多最多 有 个 9已知二次函数 y=x 2+2x+m
4、的部分图象如图所示，则关于 x 的一元二次方程x2+2x+m=0 的解 为 10如图，在平面直角坐标系中，二次函数 y=ax 2+c(a0)的图象过正方形 ABOC 的三个顶点 A，B，C， 则 ac 的值是_. 11已知抛物线cbxaxy 2 与抛物线73 2 xxy的形状相同，顶点在直线1x上，且顶点 到x轴的距离为 5，则此抛物线的解析式为 . 12已知二次函数 2 21yxaa， （a为常数） ，当a取不同的值时，其图象构成一个“抛物线 系”下图分别是当1a，0a，1a ，2a时二次函数的图象.它们的顶点在一条直线上， 这条直线的解析式是y . 三、解答题三、解答题 13已知函数 y=
5、mx 26x1（m 是常数） 第 4 页 共 10 页 求证：不论 m 为何值，该函数的图象都经过 y 轴上的一个定点； 若该函数的图象与 x 轴只有一个交点，求 m 的值 14. 如图， 直线33 xy交x轴于 A 点， 交y轴于 B 点， 过 A、 B 两点的抛物线交x轴于另一点 C （3,0） . 求抛物线的解析式； 在抛物线的对称轴上是否存在点 Q，使ABQ 是等腰三角形？若存在，求出符合条件的 Q 点坐标； 若不存在，请说明理由. 15如图，抛物线y= 2 1 x 2+bx2 与 x轴交于A、B两点，与y轴交于C点，且A（一 1，0） 求抛物线的解析式及顶点D的坐标； 判断ABC的形
6、状，证明你的结论； 点M(m，0)是x轴上的一个动点，当CM+DM的值最小时，求m的值 16. 如图（1） ，矩形 ABCD 的一边 BC 在直角坐标系中 x 轴上，折叠边 AD,使点 D 落在 x 轴上点 F 处，折 痕为 AE，已知 AB=8，AD=10，并设点 B 坐标为（m,0） ，其中 m0. 第 15 题图 y x O C B A 第 5 页 共 10 页 X1 X2 X3 y1 y2 y3 （1）求点 E、F 的坐标（用含 m 的式子表示） ； （2）连接 OA，若OAF 是等腰三角形，求 m 的值； （3）如图（2） ，设抛物线 y=a(xm6) 2+h 经过 A、E 两点，其
7、顶点为 M，连接 AM，若OAM=90， 求 a、h、m 的值. 【答案与解析答案与解析】 一、选择题一、选择题 1.【答案】C； 2.【答案】B； 【解析】利用图象法解，如图所示，y3最大，由反比例函数的性质，在同一象限，k0 时，y 随着 x 的增大而减小，易得 312 yyy 3.【答案】C ； 【解析】两个解析式的比例系数都是 k，那么分两种情况讨论一：k0 时 y k x 图像经过一、三象限， ykxk 中，k0 故图像经过一、三、四象限，符合条件的只有 C，k0 时 y k x 的图像分 布在二、四象限，ykxk 中k0 故图像经过一、二、四象限，此时 A，B，D 选项都不符合 条
8、件 4.【答案】A； 【解析】由抛物线开口方向判定a的符号，由对称轴的位置判定b的符号，由抛物线与y轴交点位置 判定c的符号.由抛物线与x轴的交点个数判定acb4 2 的符号，1 2 b x a ，a0， ba20.若x轴标出了 1 和1，则结合函数值可判定cba、cba 、 cba24 第 6 页 共 10 页 的符号. 5.【答案】C ； 【解析】这是一个动点问题.很容易由ADEDPC 得到 AEAD = CDDP ，从而得出表达式 12 y x ；也可 连结 PA，由 APDABCD 1 =S 2 S 矩形 得到表达式 12 y x ，排除(A)、(B).因为点 P 在 BC 边上运动，
9、 当点 P 与点 C 重合时，DP 与边 DC 重合，此时 DP 最短，x=3；当点 P 与点 B 重合时，DP 与对 角线 BD 重合，此时 DP 最长，x=5，即 x 的临界值是 3 和 5.又因为当 x 取 3 和 5 时，线段 AE 的长可具体求出，因此 x 的取值范围是 3x5.正确答案选(C). 6.【答案】A； 【解析】正方形 OABC，点 B 在函数 1 y x 上(x0) 设 B（x,y），z 则 x=y,由 1 y x =x 解得，x=1 正方形 OABC 边长为 1. E 点在曲线 1 y x 上，设 1 ( ,)m m , 由正方形 ADEF 可知，AD= DE 即 m
10、-1= 1 m ， 解得 51 2 m (负根已舍) AD=m-1= 51 2 m ，即正方形 ADEF 的边长为 51 2 m 点 E 坐标为 5151 (,) 22 ，故选 A. 二、填空题二、填空题 7 【答案】(4025, 3) )； 【解析】 1232013 (1, 3),(1 2, 3),(1 22, 3),(1 2012 2, 3).PPPP 8 【答案】4； 第 7 页 共 10 页 【解析】C1（3,0） 、C2（2,0） 、C3（-8,0） 、C4（ 7 6 ,0）. 9 【答案】x1=1，x2=3； 【解析】依题意得二次函数 y=x 2+2x+m 的对称轴为 x=1，与
11、x 轴的一个交点为（3，0） ， 抛物线与 x 轴的另一个交点横坐标为 1（31）=1， 交点坐标为（1，0） 当 x=1 或 x=3 时，函数值 y=0，即x 2+2x+m=0， 关于 x 的一元二次方程x 2+2x+m=0 的解为 x 1=1，x2=3 10 【答案】-2； 【解析】由题意得 A（0，c）,C ( , ) 2 2 c c ，把 C ( , ) 2 2 c c 的坐标代入 y=ax 2+c 得 ac=-2. 11 【答案】5) 1( 2 xy或5) 1( 2 xy或5) 1( 2 xy或5) 1( 2 xy； 【解析】1a，顶点（1，5）或（1，5）. 因此5) 1( 2 x
12、y或5) 1( 2 xy或5) 1( 2 xy或5) 1( 2 xy. 12 【答案】1 2 1 x； 【解析】可以取 1a ， 0a 时，分别求出抛物线的两个顶点，然后带入 y=kx+b，求出解析式. 三、解答题三、解答题 13.【答案与解析】 解：当 x=0 时，1y 所以不论m为何值，函数 2 61ymxx的图象经过y轴上的一个定点（0，1） 当0m时，函数61yx 的图象与x轴只有一个交点； 当0m时， 若函数 2 61ymxx的图象与x轴只有一个交点， 则方程 2 610mxx 有两 个相等的实数根，所以 2 ( 6)40m，9m 综上，若函数 2 61ymxx的图象与x轴只有一个交
13、点，则m的值为 0 或 9 14.【答案与解析】 解： （1）设抛物线的解析式为：y=ax 2+bx+c。 直线33 xy交x轴于 A 点，交y轴于 B 点， A 点坐标为（-1,0） 、B 点坐标为（0,3）. 又抛物线经过 A、B、C 三点， 第 8 页 共 10 页 0 930 3 abc abc c ，解得： 1 2 3 a b c ， 抛物线的解析式为：y=-x 2+2x+3 （2）y=-x 2+2x+3= 2 (1)4x，该抛物线的对称轴为 x=1 设 Q 点坐标为（1，m） ，则 22 4,1 (3)AQmBQm，又10AB . 当 AB=AQ 时， 2 410m，解得：6m ，
14、Q 点坐标为（1，6）或（1，6） ； 当 AB=BQ 时， 2 101 (3)m，解得： 12 0,6mm，Q 点坐标为（1，0）或（1，6） ； 当 AQ=BQ 时， 22 41 (3)mm，解得：1m，Q 点坐标为（1，1） 抛物线的对称轴上是存在着点 Q（1，6） 、 （1，6） 、 （1，0） 、 （1，6） 、 （1，1） ， 使ABQ 是等腰三角形 15.【答案与解析】 （1）点 A（-1，0）在抛物线y= 2 1 x 2 + bx-2 上， 2 1 (-1 ) 2 + b (-1) 2 = 0，解得 b = 2 3 抛物线的解析式为y= 2 1 x 2- 2 3 x-2. y=
15、 2 1 x 2- 2 3 x-2 = 2 1 ( x 2 -3x- 4 ) = 2 1 (x- 2 3 ) 2- 8 25 , 顶点 D 的坐标为 ( 2 3 , - 8 25 ). （2）当x = 0 时y = -2, C（0，-2） ，OC = 2。 当y = 0 时， 2 1 x 2- 2 3 x-2 = 0， x1 = -1, x2 = 4, B (4,0) OA = 1, OB = 4, AB = 5. AB 2 = 25, AC2 = OA2 + OC2 = 5, BC2 = OC2 + OB2 = 20, AC 2 +BC2 = AB2. ABC 是直角三角形. （3）作出点C
16、关于x轴的对称点C，则C（0，2） ，OC=2，连接CD交x轴于点M，根据轴对 称性及两点之间线段最短可知，MC + MD的值最小。 第 9 页 共 10 页 解法一：设抛物线的对称轴交x轴于点E. EDy轴, OCM=EDM,COM=DEM COMDEM. ED CO EM OM 8 25 2 2 3 m m ，m = 41 24 解法二：设直线CD的解析式为y = kx + n , 则 8 25 2 3 2 nk n ，解得n = 2, 12 41 k . 2 12 41 xy . 当y = 0 时， 02 12 41 x， 41 24 x . 41 24 m. 16.【答案与解析】 解：
17、 （1）四边形 ABCD 是矩形， AD=BC=10，AB=CD=8，D=DCB=ABC=90. 由折叠对称性：AF=AD=10，FE=DE. 在 RtABF 中，BF= 2222 1086AFAB. FC=4. 在 RtECF 中，4 2+（8-x）2=x2，解得 x=5. CE=8-x=3. B（m，0）,E(m+10,3),F（m+6,0）. 第 10 页 共 10 页 （2）分三种情形讨论： 若 AO=AF，ABOF，OB=BF=6.m=6. 若 OF=AF，则 m+6=10，解得 m=4. 若 AO=OF，在 RtAOB 中，AO 2=OB2+AB2=m2+64， （m+6） 2= m2+64，解得 m=7 3 . 综合得 m=6 或 4 或 7 3 . （3）由（1）知 A(m,8)，E(m+10,3). 依题意，得 2 2 (6)8 (106)3 a mmh a mmh ， 解得 1 , 4 1. a h M（m+6，1）. 设对称轴交 AD 于 G. G（m+6,8） ，AG=6，GM=8（1）=9. OAB+BAM=90，BAM+MAG=90， OAB=MAG. 又ABO=MGA=90， AOBAMG. OBAB MGAG ，即 8 96 m . m=12.
