1、第 1 页 共 10 页 中考中考冲刺冲刺：图表信息型问题图表信息型问题知识讲解（知识讲解（提高提高） 【中考展望】【中考展望】 图表信息题是指通过图形、图象或图表及一定的文字说明来提供问题情景的一类试题，它是近几年 全国各省市中考所展示的一种新题型，这类试题形式多样，取材广泛，可增加试题的灵活性和趣味性， 其发展前景非常广阔用好题中提供的信息，有利于提高学生分析、解决简单实际问题的能力，同时也 是培养现代公民素质的一条重要途径 【方法点拨】【方法点拨】 1 1图象信息题图象信息题 题型特点：这类题是中考试卷中出现频率较高的题型之一，它是通过图象呈现问题中两个变量之间 的数量关系，主要考查学生
2、对函数思想和数形结合思想的掌握程度 解题策略：解答这类问题，在弄清题意的基础上，弄清两坐标轴所代表的含义，并对图象的形状、 位置、发展变化趋势等捕捉提炼有效信息，解决相关问题 2 2图表信息题图表信息题 图表信息题是指通过图表的形式提供信息，这些信息一般以数据形式居多，其主要考查学生对图表 数据的分析、比较、判断和结论的归纳能力，要求学生有较强的定量分析和定性概括能力 图表信息题是中考常见的一种题型，它是通过图象、图形及表格等形式给出信息的一种新题型，在 解决图表信息题的时候要注意以下几点： 1、细读图表： （1）注重整体阅读.先对材料或图表资料等有一个整体的了解，把握大体方向.要通 过整体阅
3、读，搜索有效信息； （2）重视数据变化.数据的变化往往说明了某项问题，而这可能正是这个 材料的重要之处； （3）注意图表细节.图表中一些细节不能忽视，它往往起提示作用，如图表下的“注” “数字单位”等. 2、审清要求：图表题往往对答题有一定的要求，根据考题要求进行回答，才能有的放矢.题目要求 包往往括字数句数限制、比较对象、变化情况等. 3、准确表达解答图表题需要用简明的语言进行概括.解答前，要正确分析图表中所列内容的相互联 系，从中找出规律性的东西，再归纳概括为一个结论.在表述时要有具体的数据比较、分析，要客观地 反映图表包含的信息，特别要注意题目中的特殊限制. 【典型例题】【典型例题】 类
4、型一、图象信息题类型一、图象信息题 1如图所示，A、B、C、D 为O 的四等分点，动点 P 从圆心 O 出发，沿 OCDO 路线作匀速运 动设运动时间为 t(s)，APBy()，则下列图象中表示 y 与 t 之间函数关系最恰当的是 ( ) 第 2 页 共 10 页 【思路点拨】 根据动点 P 在 OC 上运动时，APB 逐渐减小，当 P 在 DC上运动时，APB 不变，当 P 在 DO 上运 动时，APB 逐渐增大，即可得出答案 【答案与解析】 解：当动点 P 在 OC 上运动时，APB 逐渐减小； 当 P 在DC上运动时，APB 不变； 当 P 在 DO 上运动时，APB 逐渐增大 故选 C
5、 【总结升华】 本题主要考查了动点问题的函数图象， 用到的知识点是圆周角、 圆内的角及函数图象认识的问题 要 能根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件，结合实际意义画出正确 的图象 2甲、乙两同学骑自行车从 A 地沿同一条路到 B 地，已知乙比甲先出发，他们离出发地的距离 s （km）和骑行时间 t（h）之间的函数关系如图所示给出下列说法： （1）他们都骑行了 20km； （2）乙在途中停留了 0.5h； （3）甲、乙两人同时到达目的地； （4）相遇后，甲的速度乙的速度 根据图象信息，以上说法正确的有（ ） A.1 个 B.2 个 C.3 个 D.4 个 【思路点拨
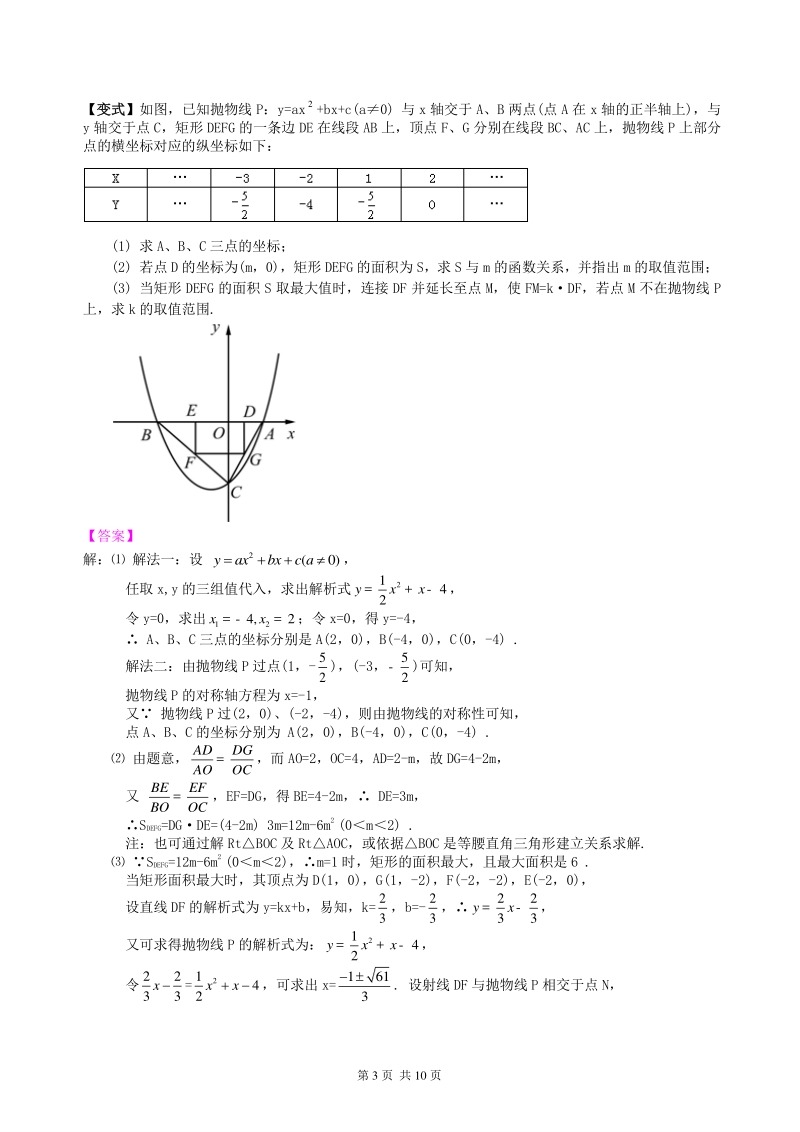
6、】 根据图象上特殊点的坐标和实际意义即可做出判断 【答案与解析】 解：由图可获取的信息是： 他们都骑行了 20km； 乙在途中停留了 0.5h； 相遇后，甲的速度乙的速度，所以甲比乙早 0.5 小时到达目的地， 所以（1） （2）正确 故选 B 【总结升华】 此题考查了学生从图象中读取信息的数形结合能力同学们要注意分析其中的“关键点”，还要善于分 析各图象的变化趋势 举一反三：举一反三： 第 3 页 共 10 页 【变式变式】如图，已知抛物线 P：y=ax 2 +bx+c(a0) 与 x 轴交于 A、B 两点(点 A 在 x 轴的正半轴上)，与 y 轴交于点 C，矩形 DEFG 的一条边 DE
7、 在线段 AB 上，顶点 F、G 分别在线段 BC、AC 上，抛物线 P 上部分 点的横坐标对应的纵坐标如下： (1) 求 A、B、C 三点的坐标； (2) 若点 D 的坐标为(m，0)，矩形 DEFG 的面积为 S，求 S 与 m 的函数关系，并指出 m 的取值范围； (3) 当矩形 DEFG 的面积 S 取最大值时，连接 DF 并延长至点 M，使 FM=kDF，若点 M 不在抛物线 P 上，求 k 的取值范围. 【答案】 解： 解法一：设 2 (0)yaxbxc a， 任取 x,y 的三组值代入，求出解析式 2 1 4 2 yxx=+-， 令 y=0，求出 12 4,2xx= -=；令 x
8、=0，得 y=-4， A、B、C 三点的坐标分别是 A(2，0)，B(-4，0)，C(0，-4) . 解法二：由抛物线 P 过点(1，- 5 2 )，(-3， 5 2 -)可知， 抛物线 P 的对称轴方程为 x=-1， 又 抛物线 P 过(2，0)、(-2，-4)，则由抛物线的对称性可知， 点 A、B、C 的坐标分别为 A(2，0)，B(-4，0)，C(0，-4) . 由题意， ADDG AOOC =，而 AO=2，OC=4，AD=2-m，故 DG=4-2m， 又 BEEF BOOC =，EF=DG，得 BE=4-2m， DE=3m， SDEFG=DGDE=(4-2m) 3m=12m-6m 2
9、 (0m2) . 注：也可通过解 RtBOC 及 RtAOC，或依据BOC 是等腰直角三角形建立关系求解. SDEFG=12m-6m 2 (0m2)，m=1 时，矩形的面积最大，且最大面积是 6 . 当矩形面积最大时，其顶点为 D(1，0)，G(1，-2)，F(-2，-2)，E(-2，0)， 设直线 DF 的解析式为 y=kx+b，易知，k= 2 3 ，b=- 2 3 ， 22 33 yx=-， 又可求得抛物线 P 的解析式为： 2 1 4 2 yxx=+-， 令 22 33 x = 2 1 4 2 xx，可求出 x= 161 3 . 设射线 DF 与抛物线 P 相交于点 N， 第 4 页 共
10、 10 页 则 N 的横坐标为 161 3 - ，过 N 作 x 轴的垂线交 x 轴于 H，有 FNHE DFDE = 161 2 3 3 = 561 9 ， 点 M 不在抛物线 P 上，即点 M 不与 N 重合时，此时 k 的取值范围是 k 561 9 -+ 且 k0. 类型二、图表信息题类型二、图表信息题 3为减少环境污染，自 2008 年 6 月 1 日起，全国的商品零售场所开始实行“塑料购物袋有偿使用 制度”(以下简称“限塑令”)某班同学于 6 月上旬的一天在某超市门口采用问卷调查的方式，随机调 查了“限塑令”实施前后，顾客在该超市用购物袋的情况，以下是根据 100 位顾客的 100
11、份有效答卷画 出的统计图表的一部分： 请你根据以上信息解答下列问题： (1)补全图， “限塑令”实施前，如果每天约有 2000 人次到该超市购物根据这 100 位顾客平均一 次购物使用塑料购物袋的平均数，估计这个超市每天需要为顾客提供多少个塑料购物袋? (2)补全图，并根据统计图和统计表说明，购物时怎样选用购物袋，塑料购物袋使用后怎样处理， 能对环境保护带来积极的影响 【思路点拨】 （1）根据调查的总人数 100 人，结合其它部分数据即可计算出 5 个对应的频数是 100-90=10；然后首先 计算样本平均数，再进一步计算 2000 人需要的塑料袋； （2）根据总百分比是 1 即可计算收费塑料
12、购物袋占：1-75%=25%；结合两个统计图中的数据进行合理分 第 5 页 共 10 页 析，提出合理化建议即可 【答案与解析】 解：(1)如图所示 “限塑令”实施前，平均一次购物使用不同数量塑料购物袋的人数统计图 9 1 37 226 3 11 4 10 54 63 7300 3 100100 这 100 位顾客平均一次购物使用塑料购物袋的平均数为 3 个 200036000(个) 估计这个超市每天需要为顾客提供 6000 个塑料购物袋 (2)图中，使用收费塑料购物袋的人数所占百分比为 25 由上图和统计表可知，购物时应尽量使用自备袋和押金式环保袋，少用塑料购物袋；塑料购物袋应 尽量循环使用
13、，以便减少塑料购物袋的使用量，为环保做贡献 【总结升华】 此题是社会上的热门话题与统计相结合的一道考题，考查了学生对图表绘制过程的理解、阅读图表并提 取有用信息的技能，借助数据处理结果做合理推测的能力 4在某次人才交流会上，应聘人数和招聘人数分别居前 5 位的行业列表如下： 第 6 页 共 10 页 如果用同一行业应聘人数与招聘人数比值的大小来衡量该行业的就业情况，那么根据表中数据，对 上述行业的就业情况判断正确的是( ) A计算机行业好于其他行业 B贸易行业好于化工行业 C机械行业好于营销行业 D建筑行业好于物流行业 【思路点拨】 本题综合考查统计部分的有关知识，通过统计表可以得到应聘人数与
14、招聘人数，进而通过计算应聘 人数与招聘人数的比值大小来衡量该行业的就业情况，比值越小越容易就业，比值越大越不容易就业， 通过计算即可求解 【答案与解析】 解：计算机行业比值为 1.83； 机械行业比值为 2.29； 营销行业比值为 1.50； 建筑行业为 0； 化工行业为 0； 而物流行业与贸易行业的比值为无穷大， 所以此题应选 D 【总结升华】 本题综合考查统计部分的有关知识，通过统计表可以得到应聘人数与招聘人数，进而通过计算应聘 人数与招聘人数的比值大小来衡量该行业的就业情况，比值越小越容易就业，比值越大越不容易就业 举一反三：举一反三： 【变式变式】下表为抄录北京奥运会官方票务网公布的三
15、种球类比赛的部分门票价格，某公司购买的门票种 类、数量绘制的条形统计图如下图. 第 7 页 共 10 页 依据上列图、表，回答下列问题： （1）其中观看男篮比赛的门票有 张；观看乒乓球比赛的门票占全部门票的 %； （2）公司决定采用随机抽取的方式把门票分配给 100 名员工，在看不到门票的条件下，每人抽取 一张（假设所有的门票形状、大小、质地等完全相同且充分洗匀） ，问员工小亮抽到男篮门票的概率 是 ； （3）若购买乒乓球门票的总款数占全部门票总款数的 8 1 ，试求每张乒乓球门票的价格. 【答案】 （1）30，20； （2） 3 10 ； （3）解法一：依题意，有 x x 205080030
16、1000 20 = 1 8 . 解得x =500 . 经检验，x =500 是原方程的解. 答：每张乒乓球门票的价格为 500 元. 解法二：依题意，有x2050800301000= x208. 解得x =500 . 答：每张乒乓球门票的价格为 500 元. 类型三、类型三、从表格、数字中寻求规律从表格、数字中寻求规律 5我市某工艺厂为配合北京奥运，设计了一款成本为 20 元件的工艺品投放市场进行试销经过 调查，得到如下数据： (1)把上表中 x、y 的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想 y 与 x 的函数关系，并求出函数关系式； (2)当销售单价定为多少时，工
17、艺厂试销该工艺品每天获得利润最大?最大利润多少?(利润销售总 价成本总价) (3)当地物价部门规定，该工艺品销售单价最高不能超过 45 元/件，那么销售单价定为多少时，工 艺厂试销该工艺品每天获得利润最大? 第 8 页 共 10 页 【思路点拨】 从表格中的数据我们可以看出当 x 增加 10 时，对应 y 的值减小 100，所以 y 与 x 之间可能是一次函 数的关系，我们可以根据图象发现这些点在一条直线上，所以 y 与 x 之间是一次函数的关系，然后设出 一次函数关系式，求出其关系式. 【答案与解析】 （1）画图如图； 由图可猜想y与x是一次函数关系， 设这个一次函数为y= kx+b（k0）
18、 这个一次函数的图象经过（30，500） 、 （40，400）这两点， 50030 40040 kb kb 解得 10 800 k b 函数关系式是：y=10x+800 （2）设工艺厂试销该工艺品每天获得的利润是 W 元，依题意得 W=（x20） （10x+800）=10x 2 +1000x-16000 第 9 页 共 10 页 =10（x50） 2 +9000 当x=50 时，W 有最大值 9000 所以，当销售单价定为 50 元件时，工艺厂试销该工艺品每天获得的利润最大，最大利润是 9000 元 （3）对于函数 W=10（x50） 2 +9000， 当x45 时，W 的值随着 x 值的增大
19、而增大， 销售单价定为 45 元件时，工艺厂试销该工艺品每天获得的利润最大 【总结升华】 能从表格、数字中发现两个量之间存在规律，归纳出相应的关系式是关键. 举一反三：举一反三： 【变式变式】某绿色无公害蔬菜基地有甲、乙两种植户，他们种植了 A、B 两类蔬菜，两 种植户种植的两类蔬菜的种植面积与总收入如下表： 说明：不同种植户种植的同类蔬菜每亩平均收入相等 求 A、两类蔬菜每亩平均收入各是多少元？ 某种植户准备租 20 亩地用来种植 A、两类蔬菜，为了使总 收入不低于 63000 元，且种植类蔬菜的面积多于种植类蔬 菜的面积（两类蔬菜的种植面积均为整数） ，求该种植户所有租 地方案. 【答案】 解：（1）设 A、B 两类蔬菜每亩平均收入分别是 x 元，y 元 由题意得： 解得： 答：A、B 两类蔬菜每亩平均收入分别是 3000 元，3500 元 （2）设用来种植 A 类蔬菜的面积 a 亩，则用来种植 B 类蔬菜的面积为（20-a）亩由题意得： 第 10 页 共 10 页 解得：10a14 a 取整数为：11、12、13、14 租地方案为： 类别 种植面积 单位：（亩） A 11 12 13 14 B 9 8 7 6
