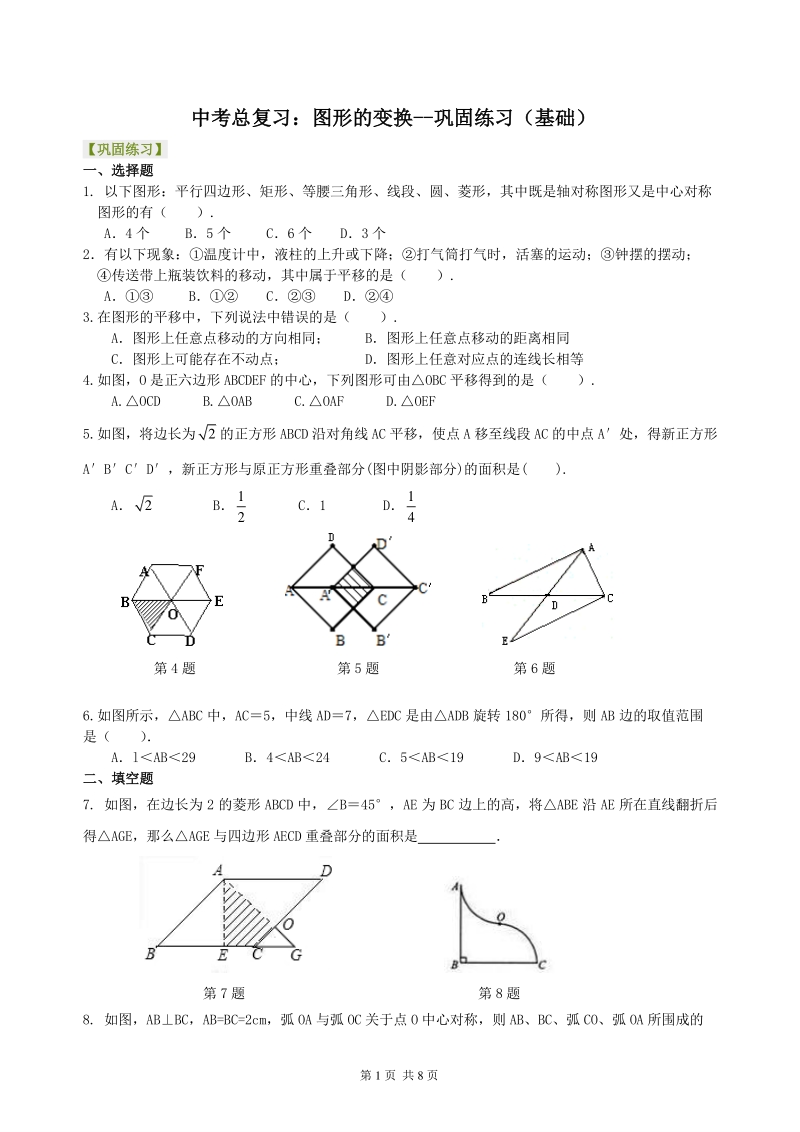
1、第 1 页 共 8 页 中考总复习：图形的变换中考总复习：图形的变换-巩固练习巩固练习（基础）（基础） 【巩固练习】【巩固练习】 一、一、选择题选择题 1. 以下图形：平行四边形、矩形、等腰三角形、线段、圆、菱形，其中既是轴对称图形又是中心对称 图形的有（ ）. A4 个 B5 个 C6 个 D3 个 2有以下现象：温度计中，液柱的上升或下降；打气筒打气时，活塞的运动；钟摆的摆动； 传送带上瓶装饮料的移动，其中属于平移的是（ ）. A B C D 3.在图形的平移中，下列说法中错误的是（ ）. A图形上任意点移动的方向相同； B图形上任意点移动的距离相同 C图形上可能存在不动点； D图形上任意
2、对应点的连线长相等 4.如图，O 是正六边形 ABCDEF 的中心，下列图形可由OBC 平移得到的是（ ）. A.OCD B.OAB C.OAF D.OEF 5.如图，将边长为2的正方形 ABCD 沿对角线 AC 平移，使点 A 移至线段 AC 的中点 A处，得新正方形 ABCD，新正方形与原正方形重叠部分(图中阴影部分)的面积是( ). A2 B 1 2 C1 D 1 4 第 4 题 第 5 题 第 6 题 6.如图所示，ABC 中，AC5，中线 AD7，EDC 是由ADB 旋转 180所得，则 AB 边的取值范围 是（ ） AlAB29 B4AB24 C5AB19 D9AB19 二、二、填
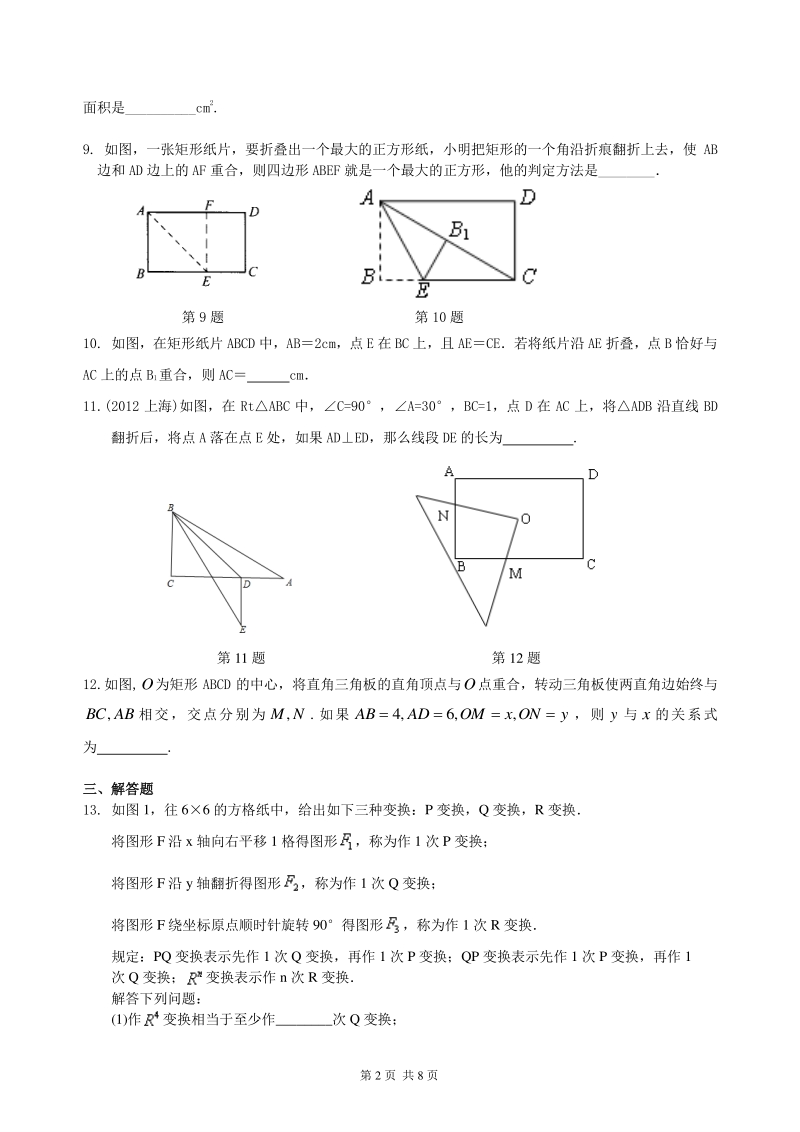
3、空题填空题 7. 如图，在边长为 2 的菱形 ABCD 中，B45，AE 为 BC 边上的高，将ABE 沿 AE 所在直线翻折后 得AGE，那么AGE 与四边形 AECD 重叠部分的面积是 第 7 题 第 8 题 8. 如图，ABBC，AB=BC=2cm，弧 OA 与弧 OC 关于点 O 中心对称，则 AB、BC、弧 CO、弧 OA 所围成的 第 2 页 共 8 页 面积是_cm 2. 9. 如图，一张矩形纸片，要折叠出一个最大的正方形纸，小明把矩形的一个角沿折痕翻折上去，使 AB 边和 AD 边上的 AF 重合，则四边形 ABEF 就是一个最大的正方形，他的判定方法是_ 第 9 题 第 10
4、 题 10. 如图，在矩形纸片 ABCD 中，AB2cm，点 E 在 BC 上，且 AECE若将纸片沿 AE 折叠，点 B 恰好与 AC 上的点 B1重合，则 AC cm 11.(2012 上海)如图，在 RtABC 中，C=90，A=30，BC=1，点 D 在 AC 上，将ADB 沿直线 BD 翻折后，将点 A 落在点 E 处，如果 ADED，那么线段 DE 的长为 . 第 11 题 第 12 题 12.如图,O为矩形 ABCD 的中心，将直角三角板的直角顶点与O点重合，转动三角板使两直角边始终与 ABBC,相交，交点分别为NM,.如果yONxOMADAB, 6, 4，则y与x的关系式 为
5、. 三、解答三、解答题题 13. 如图 1，往 66 的方格纸中，给出如下三种变换：P 变换，Q 变换，R 变换 将图形 F 沿 x 轴向右平移 1 格得图形，称为作 1 次 P 变换； 将图形 F 沿 y 轴翻折得图形，称为作 1 次 Q 变换； 将图形 F 绕坐标原点顺时针旋转 90得图形，称为作 1 次 R 变换 规定：PQ 变换表示先作 1 次 Q 变换，再作 1 次 P 变换；QP 变换表示先作 1 次 P 变换，再作 1 次 Q 变换；变换表示作 n 次 R 变换 解答下列问题： (1)作变换相当于至少作_次 Q 变换； 第 3 页 共 8 页 (2)请在图 2 中画出图形 F 作
6、变换后得到的图形； (3)PQ 变换与 QP 变换是否是相同的变换？请在图 3 中画出 PQ 变换后得到的图形，在图 4 中 画出 QP 变换后得到的图形 14.把两个全等的等腰直角三角板 ABC 和 EFG（其直角边长均为 4）叠放在一起（如图） ，且使三角 板 EFG 的直角顶点 G 与三角板 ABC 的斜边中点 O 重合.现将三角板 EFG 绕 O 点顺时针方向旋转（旋 转角 满足条件：0 90 )，四边形 CHGK 是旋转过程中两三角板的重叠部分（如图）. (1)在上述旋转过程中， BH 与 CK 有怎样的数量关系？四边形 CHGK 的面积有何变化？证明你发现的结 论； (2)连接 H
7、K，在上述旋转过程中，设 BH=x， GKH 的面积为 y ，求 y 与x之间的函数关系式，并写 出自变量x的取值范围； (3)在(2)的前提下，是否存在某一位置，使 GKH 的面积恰好等于 ABC 面积的 5 16 ？若存在，求出此 时x的值；若不存在，说明理由. 15.如图，将矩形纸片 ABCD 按如下顺序进行折叠: 对折、展平, 得折痕 EF(如图); 沿 GC 折叠, 使点 B 落在 EF 上的点 B 处(如图)； 展平, 得折痕 GC(如图); 沿 GH 折叠, 使点 C 落在 DH 上的点 C 处(如图); 沿 GC 折叠(如图)； 展平, 得折痕 GC、GH(如图). (1)求图
8、中BCB 的大小； (2)图中的GCC 是正三角形吗?请说明理由. 第 4 页 共 8 页 图 A B C D G H A C 图 A BC D GH C 图 A B C D G H C 图 A B C D E F G 图 A B C D E F G B A B C D E F 图 16.已知矩形纸片ABCD，1, 2ADAB.将纸片折叠，使顶点 A 与边 CD 上的点 E 重合. （1）如果折痕 FG 分别与 AD，AB 交于点 F，G（如图（1） ） ，, 3 2 AF求 DE 的长. （2）如果折痕 FG 分别与 CD，AB 交于点 F，G（如图（2） ） ，AED的外接圆与直线 BC
9、相切，求折痕 FG 的长. 【答案与解析】【答案与解析】 一选择题一选择题 1 【答案】A 2 【答案】D. 【解析】温度计中液柱的上升或下降改变图形的大小，不属于平移； 打气筒打气时，活塞的运动属于平移； 钟摆的摆动是旋转，不属于平移； 传送带上瓶装饮料的移动符合平移的性质，属于平移 3 【答案】C. 4 【答案】C. 5 【答案】B. 【解析】平移后，正方形 ABCD对角线是正方形 ABCD 对角线的一半，因为相似形面积比是线 段比的平方，所以正方形 ABCD面积是正方形 ABCD 面积的 1 4 ，而正方形 ABCD 面积是 2，所 以正方形 ABCD面积是 1 2 . 6 【答案】D.
10、 【解析】ADB 绕点 D 旋转 180，得到EDC， 第 5 页 共 8 页 AB=EC,AD=DE，而 AD=7，AE=14， 在ACE 中，AC=5， AE-ACECAC+AE， 即 14 -5EC14+5，9AD19 二填空题二填空题 7 【答案】22-2 【解析】在边长为 2 的菱形 ABCD 中，B=45，AE 为 BC 边上的高，故 AE=2， 由折叠易得ABG 为等腰直角三角形， SABG= 1 2 BAAG=2，SABE=1，CG=2BE-BC=22-2， CO=OG=2-2，SCOG=3-22， 重叠部分的面积为 2-1-（3-22）=22-2 8 【答案】2. 【解析】连
11、结 AC，如图， ABBC，AB=BC=2cm， ABC 为等腰直角三角形， 又弧 OA 与弧 OC 关于点 O 中心对称， OA=OC，弧 OA=弧 OC， 弓形 OA 的面积=弓形 OC 的面积， AB、BC、弧 CO、弧 OA 所围成的图形的面积=三角形 ABC 的面积= 1 2 22=2（cm 2） 9 【答案】对角线平分内角的矩形是正方形. 10 【答案】4cm. 【解析】AB=2cm，AB=AB1AB1=2cm， 四边形 ABCD 是矩形，AE=CE，ABE=AB1E=90 AE=CE，AB1=B1C，AC=4cm 11.【答案】3-1 【解析】在 RtABC 中，C=90，A=3
12、0，BC=1， BC AC = 1 3 ，即 AC=3, 将ADB 沿直线 BD 翻折后，将点 A 落在点 E 处， ADB=EDB，DE=AD， ADED，CDE=ADE=90， EDB=ADB=135，CDB=EDB-CDE=135-90=45， C=90，CBD=CDB=45， CD=BC=1，DE=AD=AC-CD=3-1. 第 6 页 共 8 页 12 【答案】 3 2 yx. 三三. .综合题综合题 13 【解析】 (1).2； (2).正确画出图形； (3).变换 PQ 与变换 QP 不是相同的变换.正确画出图形，. 14 【解析】 (1).在上述旋转过程中，BH=CK，四边形
13、CHGK 的面积不变 证明：连接 CG，KH， ABC 为等腰直角三角形，O（G）为其斜边中点， CG=BG，CGAB， ACG=B=45， BGH 与CGK 均为旋转角， BGH=CGK， 在BGH 与CGK 中， BKCG CGBG BGHCGK BGHCGK（ASA） ， BH=CK，SBGH=SCGK S四边形 CHGK=SCHG+SCGK=SCHG+SBGH= 1 2 SABC= 1 2 1 2 44=4， 即：S四边形 CHGK的面积为 4，是一个定值，在旋转过程中没有变化； 第 7 页 共 8 页 （2）AC=BC=4，BH=x， CH=4-x，CK=x 由 SGHK=S四边形
14、CHGK-SCHK， 得 y=4 - 1 2 x（4-x） ， y= 1 2 x 2-2x+4 由 090，得到 BH 最大=BC=4， 0x4； （3）存在 根据题意，得 1 2 x 2-2x+4=5 16 8， 解这个方程，得 x1=1，x2=3， 即：当 x=1 或 x=3 时，GHK 的面积均等于ABC 的面积的 5 16 15 【解析】 （1）由折叠的性质知：BC=BC， 在 RtBFC 中， cosBCF= FC B C = FC BC = 1 2 ， BCF=60， 即BCB=60； （2）根据题意得：GC 平分BCC， GCB=GCC= 1 2 BCB=30， GCC=BCD-
15、BCG=60， 由折叠的性质知：GH 是线段 CC的对称轴， GC=GC， GCC是正三角形 16.【解析】在矩形 ABCD 中，AB=2，AD=1，, 3 2 AF，D=90 根据轴对称的性质，得 EF=AF= 2 3 DF=AD-AF= 1 3 在 RtDEF 中，DE= 22 213 -= 333 第 8 页 共 8 页 （2）设 AE 与 FG 的交点为 O根据轴对称的性质，得 AO=EO 取 AD 的中点 M，连接 MO则 MO= 1 2 DE，MODC 设 DE=x，则 MO= 1 2 x，在矩形 ABCD 中，C=D=90， AE 为AED 的外接圆的直径，O 为圆心 延长 MO
16、 交 BC 于点 N，则 ONCD, CNM=180-C=90, ONBC，四边形 MNCD 是矩形 MN=CD=AB=2ON=MN-MO=2- 1 2 x. AED 的外接圆与 BC 相切， ON 是AED 的外接圆的半径, OE=ON=2- 1 2 x，AE=2ON=4-x 在 RtAED 中，AD 2+DE2=AE2， 1 2+x2=（4-x）2 解这个方程，得 x=15 8 DE= 15 8 ，OE=2- 1 2 x=17 16 根据轴对称的性质，得 AEFG FOE=D=90 可得 FOEO DADE ,即 FO= 17 30 又 ABCD，EFO=AGO，FEO=GAO FEOGAOFO=GO FG=2FO=17 15 折痕 FG 的长是17 15
