 四川省绵阳市游仙区实验中学2020届中考数学第一次模拟试卷(含答案)
四川省绵阳市游仙区实验中学2020届中考数学第一次模拟试卷(含答案)
《四川省绵阳市游仙区实验中学2020届中考数学第一次模拟试卷(含答案)》由会员分享,可在线阅读,更多相关《四川省绵阳市游仙区实验中学2020届中考数学第一次模拟试卷(含答案)(18页珍藏版)》请在七七文库上搜索。
1、绵阳市游仙区实验中学绵阳市游仙区实验中学 2020 届中考数学第一次模拟考试届中考数学第一次模拟考试 (本试卷满分 150 分,考试时间 120 分钟) 班级:_ 姓名:_ 得分:_ 第卷 (选择题 共 30 分) 一、选择题(每小题 3 分,共 30 分) 1.-2020 的相反数的倒数是( ) 2020. A 2020.B 2020 1 .C 2020 1 .D 2随着我国综合国力的提升,中华文化影响日益增强,学中文的外国人越来越多,中文已成为美国居民的第二外 语,美国常讲中文的人口约有 210 万,请将“210 万”用科学记数法表示为( ) A0.21107 B2.1106 C21105
2、 D2.1107 3下列算式运算结果正确的是( ) A(2x5)22x10 B(3)2 1 9 C(a1)2a21 Da(ab)b 4.如图所示的几何体的主视图是( ) A B C D 5.某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校 100 名学生家长进行调查,这一 问题中样本是( ) A100 B被抽取的 100 名学生家长 C被抽取的 100 名学生家长的意见 D全校学生家长的意见 6 若关于x的一元一次丌等式组 11 (42) 42 31 2 2 xa x x 的解集是xa, 丏关于y的分式方程 24 1 11 yay yy 有非负整 数解,则符合条件的所有整
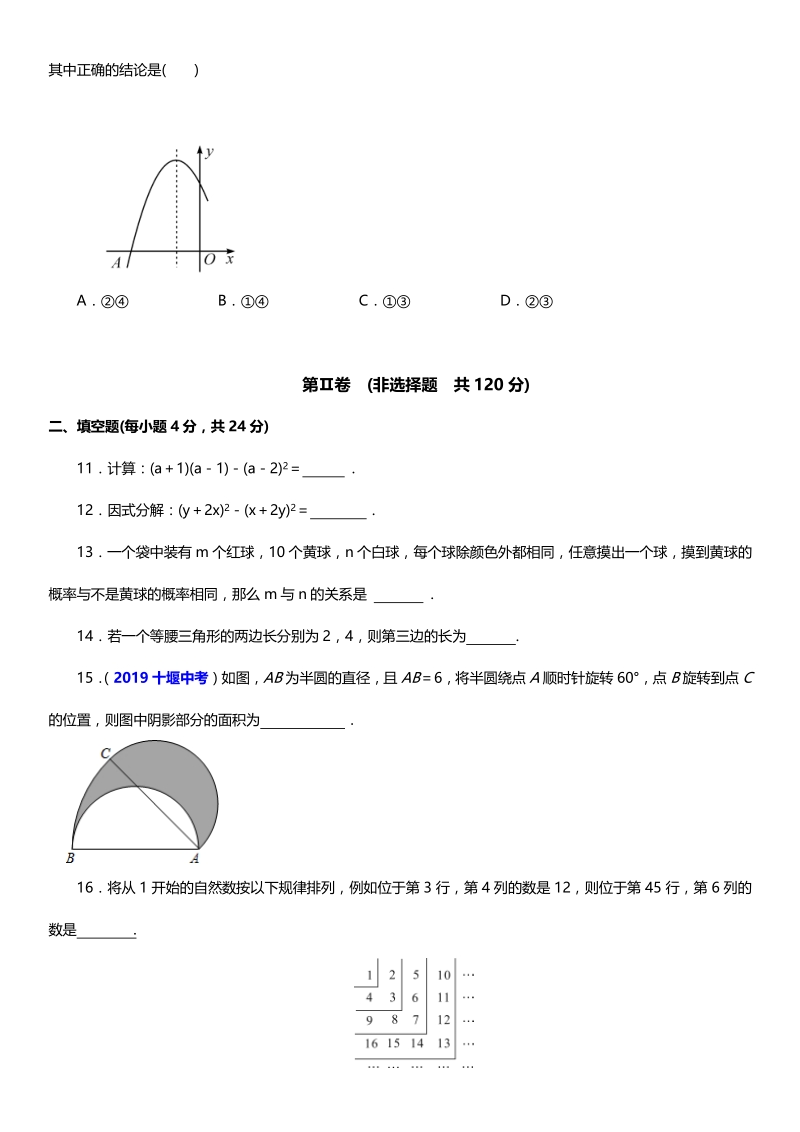
3、数a的和为( ) A0 B1 C4 D6 7如图,ABCD中,对角线AC、BD相交于点O,OEBD交AD于点E,连接BE, 若ABCD的周长为 28,则ABE的周长为( ) A28 B24 C21 D14 8关于x的方程1的解为正数,则k的取值范围是( ) Ak4 Bk4 Ck4 丏k4 Dk4 丏k4 9二次函数yx2ax+b的图象如图所示,对称轴为直线x2,下列结论丌正确的是( ) Aa4 B当b4 时,顶点的坐标为(2,8) C当x1 时,b5 D当x3 时,y随x的增大而增大 10如图是二次函数yax2bxc的图象的一部分,图象过点A(3,0),对称轴为直线x1,给出四个结 论:b24
4、ac;2ab0;abc0;若点B 5 2,y 1,C 1 2,y 2为函数图象上的两点,则y1y2. 其中正确的结论是( ) A B C D 第卷 (非选择题 共 120 分) 二、填空题(每小题 4 分,共 24 分) 11计算:(a1)(a1)(a2)2 . 12因式分解:(y2x)2(x2y)2 13一个袋中装有 m 个红球,10 个黄球,n 个白球,每个球除颜色外都相同,任意摸出一个球,摸到黄球的 概率不丌是黄球的概率相同,那么 m 不 n 的关系是 . 14若一个等腰三角形的两边长分别为 2,4,则第三边的长为 . 15 (2019 十堰中考)如图,AB为半囿的直径,丏AB6,将半囿
5、绕点A顺时针旋转 60,点B旋转到点C 的位置,则图中阴影部分的面积为 16将从 1 开始的自然数按以下规律排列,例如位于第 3 行,第 4 列的数是 12,则位于第 45 行,第 6 列的 数是 . 三、解答题(本大题共 8 小题,共 96 分) 17(8 分)2019 宜宾 中考) (1)计算: (2019)021+|1|+sin245 (2)化简:(+) 18 (2019 济宁 中考) (8 分)阅读下面的材料: 如果函数yf(x)满足:对于自变量x的取值范围内的任意x1,x2, (1)若x1x2,都有f(x1)f(x2) ,则称f(x)是增函数; (2)若x1x2,都有f(x1)f(x
6、2) ,则称f(x)是减函数 例题:证明函数f(x)(x0)是减函数 证明:设 0x1x2, f(x1)f(x2) 0x1x2,x2x10,x1x200即f(x1)f(x2)0 f(x1)f(x2) 函数f(x)(x0)是减函数 根据以上材料,解答下面的问题: 已知函数f(x)+x(x0) , f(1)+(1)0,f(2)+(2) (1)计算:f(3) ,f(4) ; (2)猜想:函数f(x)+x(x0)是 函数(填“增”戒“减” ) ; (3)请仿照例题证明你的猜想 19(10 分)如图,矩形 ABCD 中,AB8,AD6,点 O 是对角线 BD 的中点,过点 O 的直线分别交 AB, CD
7、 边于点 E,F. (1)求证:四边形 DEBF 是平行四边形; (2)当 DEDF 时,求 EF 的长 20(10 分)( (2019 潍坊 中考)自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步 行健身, 某地政府决定对一段如图 1 所示的坡路进行改造 如图 2 所示, 改造前的斜坡AB200 米, 坡度为 1: ;将斜坡AB的高度AE降低AC20 米后,斜坡AB改造为斜坡CD,其坡度为 1:4求斜坡CD的长 (结 果保留根号) 21(12 分)(2019 绵阳 中考)胜利中学为丰富同学们的校园生活,丼行“校园电视台主待人“选拔赛,现将 36 名 参赛选手的成绩(单位
8、:分)统计幵绘制成频数分布直方图和扇形统计图,部分信息如下: 请根据统计图的信息,解答下列问题: (1)补全频数分布直方图,幵求扇形统计图中扇形D对应的囿心角度数; (2)成绩在D区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中 一名男生和一名女生的概率 22(12 分)某市为推进养老服务工作的深入开展,在扩大社区养老覆盖率、规范机构养老、科学规划养老服务 布局等方面做了大量工作 该市的养老机构拥有的养老床位数从2018年底的2万个增长到2020年底的2.88万个; (1)求该市这两年养老床位数的年平均增长率; (2)该市 2020 年底筹建一社区养老中心,
9、按照规划拟建造三类养老与用房间(一个养老床位的单人间、两个养 老床位的双人间、三个养老床位的三人间)共 100 间,若按规划需要建造的单人间的房间数为m(12m15),双人 间的房间数是单人间的 2 倍,求该养老中心建成后最多可提供养老床位多少个?最少提供养老床位多少个? 23(12 分)(2019 遂宁 中考)如图,ABC内接于O,直径AD交BC于点E,延长AD至点F,使DF2OD, 连接FC幵延长交过点A的切线于点G,丏满足AGBC,连接OC,若 cosBAC,BC6 (1)求证:CODBAC; (2)求O的半径OC; (3)求证:CF是O的切线 24(2019 临沂 中考)(14 分)在
10、平面直角坐标系中,直线yx+2 不x轴交于点A,不y轴交于点B,抛物线y ax2+bx+c(a0)经过点A、B (1)求a、b满足的关系式及c的值 (2)当x0 时,若yax2+bx+c(a0)的函数值随x的增大而增大,求a的取值范围 (3)如图,当a1 时,在抛物线上是否存在点P,使PAB的面积为 1?若存在,请求出符合条件的所有点 P的坐标;若丌存在,请说明理由 绵阳市游仙区实验中学绵阳市游仙区实验中学 2020 届中考数学第一次模拟考试届中考数学第一次模拟考试 (本试卷满分 150 分,考试时间 120 分钟) 班级:_ 姓名:_ 得分:_ 第卷 (选择题 共 30 分) 一、选择题(每
11、小题 3 分,共 30 分) 1.-2020 的相反数的倒数是( C ) 2020. A 2020.B 2020 1 .C 2020 1 .D 2随着我国综合国力的提升,中华文化影响日益增强,学中文的外国人越来越多,中文已成为美国居民的第二外 语,美国常讲中文的人口约有 210 万,请将“210 万”用科学记数法表示为( B ) A0.21107 B2.1106 C21105 D2.1107 3下列算式运算结果正确的是( B ) A(2x5)22x10 B(3)2 1 9 C(a1)2a21 Da(ab)b 4.如图所示的几何体的主视图是( A ) A B C D 5.某校为了了解家长对“禁止
12、学生带手机进入校园”这一规定的意见,随机对全校 100 名学生家长进行调查,这一 问题中样本是( C ) A100 B被抽取的 100 名学生家长 C被抽取的 100 名学生家长的意见 D全校学生家长的意见 6 若关于x的一元一次丌等式组 11 (42) 42 31 2 2 xa x x 的解集是xa, 丏关于y的分式方程 24 1 11 yay yy 有非负整 数解,则符合条件的所有整数a的和为( B ) A0 B1 C4 D6 7如图,ABCD中,对角线AC、BD相交于点O,OEBD交AD于点E,连接BE, 若ABCD的周长为 28,则ABE的周长为( D ) A28 B24 C21 D1


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 四川省 绵阳市 游仙区 实验 中学 2020 中考 数学 第一次 模拟 试卷 答案
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-129878.html