1、第 1 页 共 5 页 二次函数二次函数 y=ay=a（x x- -h)h) 2 2+k(a +k(a0)0)的图的图象象与性质与性质知识讲解知识讲解（提高）（提高） 【学习目标】【学习目标】 1. .会用描点法画出二次函数 2 ()ya xhk(a、 h、 k 常数， a0)的图象 掌握抛物线 2 ()ya xhk 与 2 yax图象之间的关系； 2.熟练掌握函数 2 ()ya xhk的有关性质， 并能用函数 2 ()ya xhk的性质解决一些实际问题； 3. .经历探索 2 ()ya xhk的图象及性质的过程，体验 2 ()ya xhk与 2 yax、 2 yaxk、 2 ()ya xh之
2、间的转化过程，深刻理解数学建模思想及数形结合的思想方法 【要点梳理】【要点梳理】 要点一、要点一、函数函数 2 () (0)ya xha与函数与函数 2 ()(0)ya xhk a的图的图象象与与性质性质 1.1.函数函数 2 () (0)ya xha的图的图象象与性质与性质 2.2.函数函数 2 ()(0)ya xhk a的图的图象象与性质与性质 要点诠释：要点诠释： 二次函数 2 () + (0ya xhk a ）的图象常与直线、三角形、面积问题结合在一起，借助它的图象 与性质运用数形结合、函数、方程思想解决问题 要点二、要点二、二次二次函数的平移函数的平移 1.1.平移步骤：平移步骤：
3、将抛物线解析式转化成顶点式 2 ya xhk，确定其顶点坐标hk，； a的符号 开口方向 顶点坐标 对称轴 性质 0a 向上 0h， x=h xh时，y随x的增大而增大；xh时，y随 x的增大而减小；xh时，y有最小值0 0a 向下 0h， x=h xh时，y随x的增大而减小；xh时，y随 x的增大而增大；xh时，y有最大值0 a的符号 开口方向 顶点坐标 对称轴 性质 0a 向上 hk， x=h xh时，y随x的增大而增大；xh时，y随 x的增大而减小；xh时，y有最小值k 0a 向下 hk， x=h xh时，y随x的增大而减小；xh时，y随 x的增大而增大；xh时，y有最大值k 第 2 页
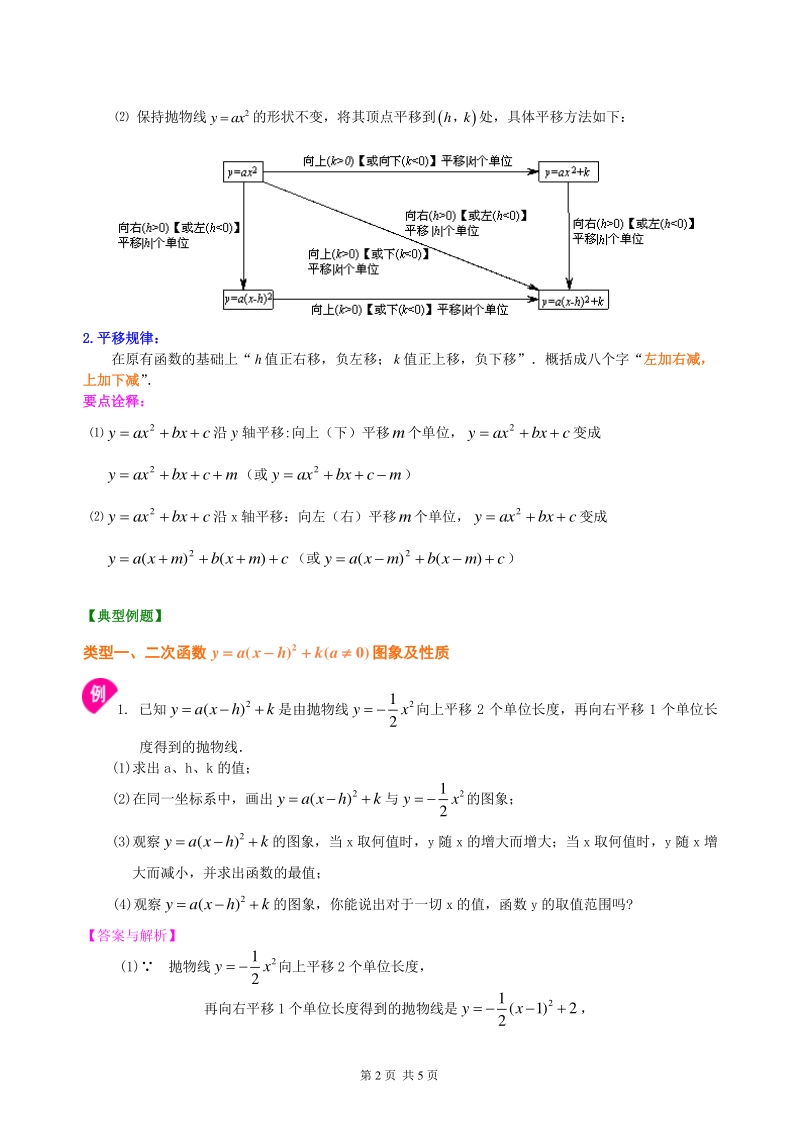
4、 共 5 页 保持抛物线 2 yax的形状不变，将其顶点平移到hk，处，具体平移方法如下： 2.2.平移规律：平移规律： 在原有函数的基础上“h值正右移，负左移；k值正上移，负下移”概括成八个字“左加右减，左加右减， 上加下减上加下减” 要点诠释：要点诠释： cbxaxy 2 沿y轴平移:向上（下）平移m个单位，cbxaxy 2 变成 mcbxaxy 2 （或mcbxaxy 2 ） cbxaxy 2 沿 x 轴平移：向左（右）平移m个单位，cbxaxy 2 变成 cmxbmxay)()( 2 （或cmxbmxay)()( 2 ） 【典型典型例题】例题】 类型一、二次函数类型一、二次函数 2 (
5、)(0)ya xhk a图图象象及性质及性质 1. 已知 2 ()ya xhk是由抛物线 2 1 2 yx 向上平移 2 个单位长度，再向右平移 1 个单位长 度得到的抛物线 (1)求出 a、h、k 的值； (2)在同一坐标系中，画出 2 ()ya xhk与 2 1 2 yx 的图象； (3)观察 2 ()ya xhk的图象，当 x 取何值时，y 随 x 的增大而增大；当 x 取何值时，y 随 x 增 大而减小，并求出函数的最值； (4)观察 2 ()ya xhk的图象，你能说出对于一切 x 的值，函数 y 的取值范围吗? 【答案与解析】 (1) 抛物线 2 1 2 yx 向上平移 2 个单位
6、长度， 再向右平移 1 个单位长度得到的抛物线是 2 1 (1)2 2 yx ， 第 3 页 共 5 页 1 2 a ，1h ，2k (2)函数 2 1 (1)2 2 yx 与 2 1 2 yx 的图象如图所示 (3)观察 2 1 (1)2 2 yx 的图象知，当1x时，y 随 x 的增大而增大； 当1x 时，y 随 x 增大而减小，当 x1 时，函数 y 有最大值是 2 (4)由图象知，对于一切 x 的值，总有函数值 y2 【总结升华】先根据平移的性质求出抛物线 2 1 2 yx 平移后的抛物线的解析式，再对比 2 ()ya xhk得到 a、h、k 的值，然后画出图象，由图象回答问题 举一反
7、三：举一反三： 【变式变式】把二次函数 2 ()ya xhk的图象先向左平移 2 个单位，再向上平移 4 个单位，得到二次函 数 2 1 (1)1 2 yx 的图象 （1）试确定a、h、k的值； （2）指出二次函数 2 ()ya xhk的开口方向，对称轴和顶点坐标，分析函数的增减性 【答案】 （1） 1 ,1,5 2 ahk .（2）开口向下，对称轴 x=1, 顶点坐标为（1，-5） ， 当 x1 时，y随x的增大而减小； 当 x1 时，y随x的增大而增大. 2. 已知函数 2 2 113 513 xx y xx ，则使 y=k 成立的 x 值恰好有三个，则 k 的值为（ ） A0 B1 C2
8、 D3 【答案】D； 【解析】函数 2 2 113 513 xx y xx 的图象如图： 第 4 页 共 5 页 ， 根据图象知道当 y=3 时，对应成立的 x 恰好有三个， k=3 故选 D 【总结升华】此题主要考查了利用二次函数的图象解决交点问题，解题的关键是把解方程的问题转换为 根据函数图象找交点的问题 类型二、二次函数类型二、二次函数 2 ()(0)ya xhk a性质的综合应用性质的综合应用 3. 如图所示，点 A、B 的坐标分别为(1，4)和(4，4)，抛物线 2 ()ya xmn的顶点在线段 AB 上移动， 与x轴交于C、 D两点(C在D的左侧)， 点C的横坐标最小值为-3， 则
9、点D的横坐标最大值为( ) A.-3 B.1 C.5 D.8 【答案】D； 【解析】要使点 C 的横坐标最小值为-3，即是当抛物线 2 ()ya xmn的顶点在点 A(1，4)时 点 C 的坐标为(-3，0)由此得 2 (1)4ya x将3x，y0 时， 2 0( 3 1)4a 所以 1 4 a 当抛物线 2 1 (1)4 4 yx 顶点在 B(4，4)时 点 D 的横坐标取最大值此时平移后的抛物线的解析式为 2 1 (4)4 4 yx 令0y ， 解得 x8 【总结升华】此题根据抛物线 2 ()ya xmn平移的性质求出 a、m、n 得到抛物线的解析式再利用 二次函数解析式求解 举一反三：举
10、一反三： 【变式】在距离地面 2m 高的某处把一物体以初速度 v0(m/s)竖直向上抛出，在不计空气阻力的情况下， 第 5 页 共 5 页 其上升高度 s(m)与抛出时间 t(s)满足：(其中 g 是常数，通常取 10m/s 2).若 v0=10m/s， 则该物体在运动过程中最高点距地面_m. 【答案】7. 4. 如图所示，抛物线 2 1 3(1)yx的顶点为 C，与 y 轴交点为 A，过点 A 作 y 轴的垂线，交抛 物线于另一点 B (1)求直线 AC 的解析式 2 ykxb； (2)求ABC 的面积； (3)当自变量 x 满足什么条件时，有 12 yy? 【答案与解析】 (1)由 2 1
11、 3(1)yx知抛物线顶点 C(-1，0)，令 x0，得3y ， (0, 3)A由待定系数法可求出3b ，3k ， 2 33yx (2) 抛物线 2 1 3(1)yx的对称轴为 x-1，根据抛物线对称性知( 2, 3)B 1 233 2 ABC S (3)根据图象知0x或1x时，有 12 yy 【总结升华】 图象都经过 A 点和 C 点，说明 A 点、C 点同时出现在两个图象上，A、C 两点的坐标均满 足两个函数的解析式，解答这类题时，要画出函数图象，结合几何图形的性质，运用数形结 合的思想和抛物线的对称性，特别要慎重处理平面直角坐标系中的坐标(数)与线段长度(形) 之间的关系，不要出现符号上的错误，充分利用函数图象弄清函数值与自变量的关系，利用 图象比较函数值的大小，或根据函数值的大小，确定自变量的变化范围
