1、第 1 页 共 10 页 锐角三角函数全章复习与巩固锐角三角函数全章复习与巩固-知识讲解知识讲解（提高）（提高） 【学习目标】【学习目标】 1.了解锐角三角函数的概念，能够正确使用 sinA 、cos A、tanA 表示直角三角形中两边的比；记忆 30、 45、60的正弦、余弦和正切的函数值，并会由一个特殊角的三角函数值求出这个角的度数； 2能够正确地使用计算器，由已知锐角的度数求出它的三角函数值，由已知三角函数值求出相应的锐角 的度数； 3理解直角三角形中边与边的关系，角与角的关系和边与角的关系，会运用勾股定理、直角三角形的两 个锐角互余、以及锐角三角函数解直角三角形，并会用解直角三角形的有
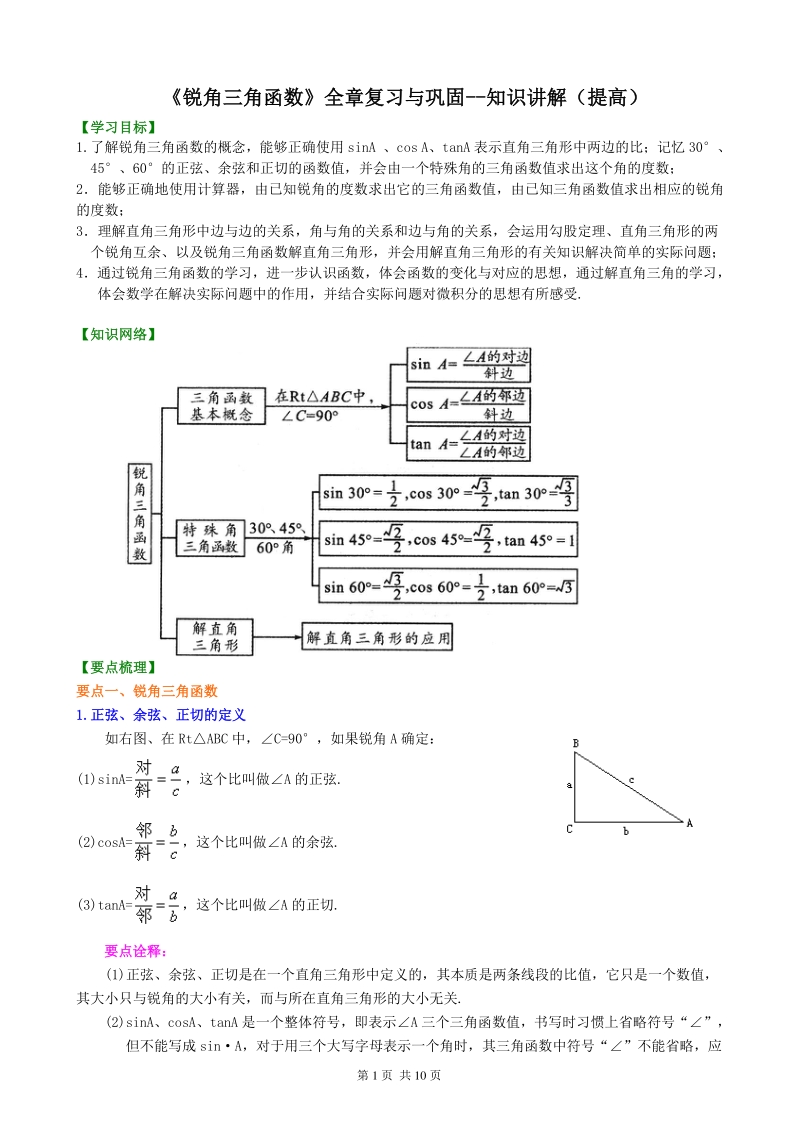
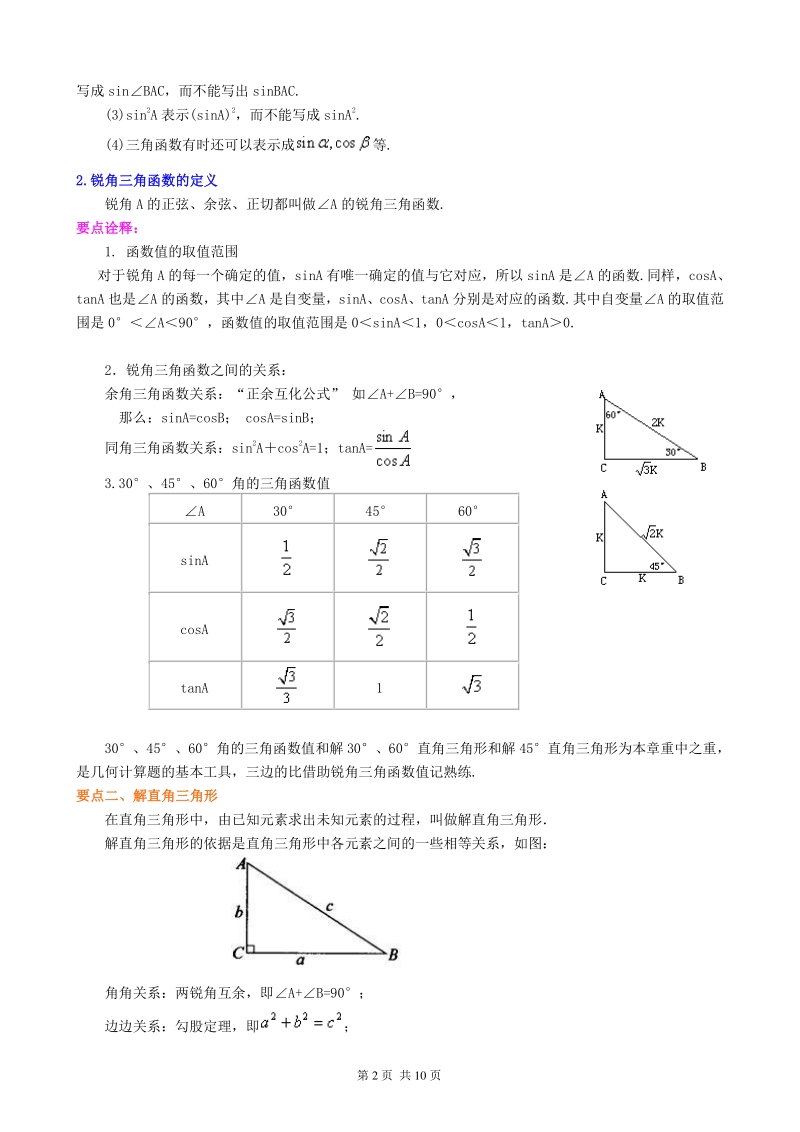
2、关知识解决简单的实际问题； 4通过锐角三角函数的学习，进一步认识函数，体会函数的变化与对应的思想，通过解直角三角的学习， 体会数学在解决实际问题中的作用，并结合实际问题对微积分的思想有所感受. 【知识网络】【知识网络】 【要点梳理】【要点梳理】 要点一、要点一、锐角三角函数锐角三角函数 1.1.正弦、余弦、正切的定义正弦、余弦、正切的定义 如右图、在 RtABC 中，C=90，如果锐角 A 确定： (1)sinA=，这个比叫做A 的正弦. (2)cosA=，这个比叫做A 的余弦. (3)tanA=，这个比叫做A 的正切. 要点诠释：要点诠释： (1)正弦、余弦、正切是在一个直角三角形中定义的，
3、其本质是两条线段的比值，它只是一个数值， 其大小只与锐角的大小有关，而与所在直角三角形的大小无关. (2)sinA、cosA、tanA 是一个整体符号，即表示A 三个三角函数值，书写时习惯上省略符号“”， 但不能写成 sinA，对于用三个大写字母表示一个角时，其三角函数中符号“”不能省略，应 第 2 页 共 10 页 写成 sinBAC，而不能写出 sinBAC. (3)sin 2A 表示(sinA)2，而不能写成 sinA2. (4)三角函数有时还可以表示成等. 2.2.锐角三角函数的定义锐角三角函数的定义 锐角 A 的正弦、余弦、正切都叫做A 的锐角三角函数. 要点诠释：要点诠释： 1.
4、函数值的取值范围 对于锐角 A 的每一个确定的值，sinA 有唯一确定的值与它对应，所以 sinA 是A 的函数.同样，cosA、 tanA 也是A 的函数，其中A 是自变量，sinA、cosA、tanA 分别是对应的函数.其中自变量A 的取值范 围是 0A90，函数值的取值范围是 0sinA1，0cosA1，tanA0. 2锐角三角函数之间的关系： 余角三角函数关系：“正余互化公式” 如A+B=90， 那么：sinA=cosB； cosA=sinB； 同角三角函数关系：sin 2Acos2A=1；tanA= 3.30、45、60角的三角函数值 A 30 45 60 sinA cosA tan
5、A 1 30、45、60角的三角函数值和解 30、60直角三角形和解 45直角三角形为本章重中之重， 是几何计算题的基本工具，三边的比借助锐角三角函数值记熟练. 要点二、要点二、解直角三角形解直角三角形 在直角三角形中，由已知元素求出未知元素的过程，叫做解直角三角形 解直角三角形的依据是直角三角形中各元素之间的一些相等关系，如图： 角角关系：两锐角互余，即A+B=90； 边边关系：勾股定理，即； 第 3 页 共 10 页 边角关系：锐角三角函数，即 要点诠释：要点诠释： 解直角三角形，可能出现的情况归纳起来只有下列两种情形： (1)已知两条边(一直角边和一斜边；两直角边)； (2)已知一条边和
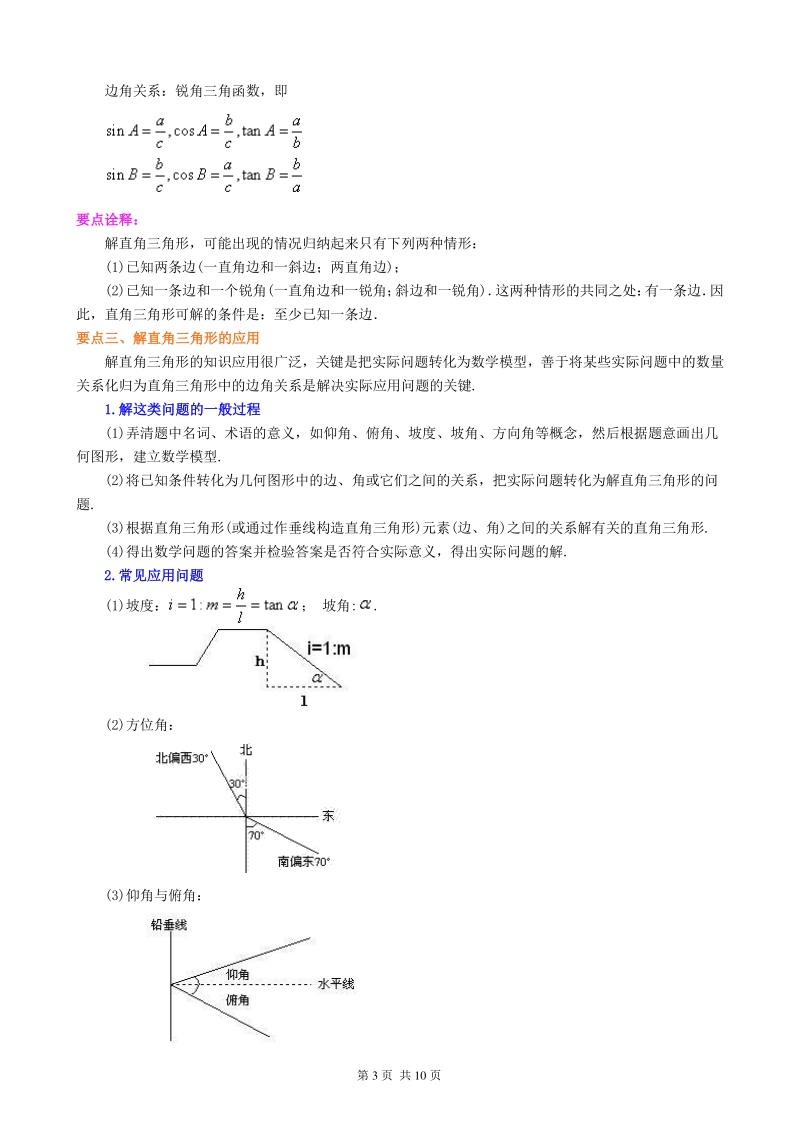
6、一个锐角(一直角边和一锐角； 斜边和一锐角) 这两种情形的共同之处： 有一条边 因 此，直角三角形可解的条件是：至少已知一条边 要点三、要点三、解直角三角形的应用解直角三角形的应用 解直角三角形的知识应用很广泛，关键是把实际问题转化为数学模型，善于将某些实际问题中的数量 关系化归为直角三角形中的边角关系是解决实际应用问题的关键. 1.1.解这类问题的一般过程解这类问题的一般过程 (1)弄清题中名词、术语的意义，如仰角、俯角、坡度、坡角、方向角等概念，然后根据题意画出几 何图形，建立数学模型. (2)将已知条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形的问 题. (3
7、)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形. (4)得出数学问题的答案并检验答案是否符合实际意义，得出实际问题的解. 2.2.常见应用问题常见应用问题 (1)坡度：； 坡角:. (2)方位角： (3)仰角与俯角： 第 4 页 共 10 页 要点诠释：要点诠释： 1解直角三角形的常见类型及解法 已知条件 解法步骤 RtABC 两 边 两直角边(a，b) 由求A， B=90A， 斜边，一直角边(如 c，a) 由求A， B=90A， 一 边 一 角 一直角边 和一锐角 锐角、邻边 (如A，b) B=90A， ， 锐角、对边 (如A，a) B=90A， ，
8、 斜边、锐角(如 c，A) B=90A， ， 2用解直角三角形的知识解决实际问题的基本方法是： 把实际问题抽象成数学问题(解直角三角形)，就是要舍去实际事物的具体内容，把事物及它们的联系 转化为图形(点、线、角等)以及图形之间的大小或位置关系 借助生活常识以及课本中一些概念(如俯角、仰角、倾斜角、坡度、坡角等)的意义，也有助于把实际 问题抽象为数学问题 当需要求解的三角形不是直角三角形时，应恰当地作高，化斜三角形为直角三角形再求解 第 5 页 共 10 页 3锐角三角函数的应用 用相似三角形边的比的计算具有一般性，适用于所有形状的三角形，而三角函数的计算是在直角三角 形中解决问题，所以在直角三
9、角形中先考虑三角函数，可以使过程简洁。 如：射影定理不能直接用，但是用等角的三角函数值相等进行代换很简单： 【典型典型例题】例题】 类型一、类型一、锐角三角函数锐角三角函数 1在 RtABC 中，C90，若将各边长度都扩大为原来的 2 倍，则A 的正弦值是( ) A扩大 2 倍 B缩小 2 倍 C扩大 4 倍 D不变 【答案】 D； 【解析】根据 A sinA 的对边 斜边 知 sinA 的值与A 的大小有关，与 A 的对边 斜边 的比值有关 当各边长度都扩大为原来的 2 倍时，其 A 的对边 斜边 的比值不变故选 D. 【总结升华】 锐角三角函数正弦、余弦和正切反映了直角三角形中边与边的关系
10、 举一反三：举一反三： 【变式变式 1 1】已知，如图，ABC中，CEAB，BDAC， 2 5 DE BC ，求 cosA及 tanA A B C D E 【答案】易证点 B、C、D、E 四点共圆，ADEABC， 第 6 页 共 10 页 cosA= 2 , 5 ADDE ABBC tanA= 21 . 2 BD AD 【变变式式2 2】 如图所示， 已知ABC是O的内接三角形， ABc， ACb， BCa， 请你证明 sinsinsin abc ABC 【答案】 证明：O 是ABC 的外接圆，设圆的半径为 R，连结 AO 并延长交O 于点 D， 连结 CD，则BD AD 是O 的直径，ACD
11、90即ADC 为直角三角形 sinsin 2 ACb BD ADR ，2 sin b R B 同理可证：2 sin a R A ，2 sin c R C 2 sinsinsin abc R ABC 类型二、类型二、 特殊角三角函数值的计算特殊角三角函数值的计算 2已知 a3，且 2 1 (4tan45)30 2 bb c ，则以 a、b、c 为边长的三角形面积等于( ) A6 B7 C8 D9 【答案】A； 【解析】根据题意知 4tan450, 1 30, 2 b bc 解得 4, 5. b c 所以 a3，b4，c5，即 222 abc，其构成的三角形为直角三角形，且C90， 所以 1 6
12、2 Sab 【总结升华】利用非负数之和等于 0 的性质，求出 b、c 的值，再利用勾股定理的逆定理判断三角形是直 角三角形，注意 tan45的值不要记错 举一反三：举一反三： 【变式】变式】计算： tan60tan45 tan60tan45 2sin60 【答案】原式= 313 2 2 3 1 = 2 33 3 第 7 页 共 10 页 类型三、类型三、 解直角三角形解直角三角形 3如图所示，在等腰 RtABC 中，C90，AC6，D 是 AC 上一点，若 1 tan 5 DBA，则 AD 的长为( ) A2 B3 C2 D1 【思路点拨】 如何用好 1 tan 5 DBA是解题关解，因此要设
13、法构造直角三角形，若所求的元素不在直角三角 形中，则应将它转化到直角三角形中去，转化的途径及方法很多，如可作辅助线构造直角三角形，或找已 知直角三角形中的边或角替代所要求的元素等 【答案】 A； 【解析】 作 DEAB 于点 E 因为ABC 为等腰直角三角形，所以A45，所以 AEDE 又设 DEx，则 AEx，由 1 tan 5 DE DBA EB 知 BE5x，所以 AB6x，由勾股定理知 AC 2+BC2AB2， 所以 6 2+62(6x)2， 2x ，AD2AE222 【总结升华】在直角三角形中，若已知两边，宜先用勾股定理求出第三边，再求锐角三角函数值；若已知 一边和角，应先求另一角，
14、再通过锐角三角函数列出含有未知元素和已知元素的等式求解 类型四类型四 、锐角锐角三角函数与相关知识的综合三角函数与相关知识的综合 4如图所示，直角ABC 中，C90，AB2 5，sin B 5 5 ，点 P 为边 BC 上一动点，PDAB， PD 交 AC 于点 D，连接 AP， (1)求 AC，BC 的长； (2)设 PC 的长为 x，ADP 的面积为 y，当 x 为何值时，y 最大，并求出最大值 【思路点拨】 第 8 页 共 10 页 (1)在 RtABC 中，由 AB2 5，sin B 5 5 AC AB ，易得 AC2，再由勾股定理求 BC (2) 1 2 ADP SAD PC ，只要
15、把 AD 用 x 表示即可求出ADP 的面积 y， 由 PDAB 可得 PCCD BCAC ，从而求出 1 2 CDx，则 1 2 2 ADx 【答案与解析】 (1)在 RtABC 中，由 5 sin 5 B ，AC2，由勾股定理得 BC4 (2)PDAB，ABCDPC， 1 2 DCAC PCBC PCx，则 22 1111 2(2)1 2244 yxxxxx ， 当 x2 时，y 有最大值，最大值是 1 【总结升华】 近几年，锐角三角函数与圆、函数、相似三角形以及方程相结合的题目在各地中考试题中出现的频 率越来越大如圆中的垂径定理，直径所对的圆周角都出现了直角或直角三角形在函数中，在直角坐
16、标 系中求点的坐标，离不开求直角三角形两直角边的问题，相似三角形中可将有些元素进行转换或替代 举一反三：举一反三： 【变式变式】 如图， 设P是矩形ABCD的AD边上一动点，PEAC于点E，PFBD于F，3AB，4AD 求PEPF的值 【答案】如图，sin1=. PE PA sin2=. PF PD 由矩形 ABCD 知1=2， 则 PE=PAsin1，PF=PDsin2,sin1= CD3 = AC5 ， 所以 PE+PF= PAsin1+ PDsin2=（PA+PD）sin1= 312 4= 55 类型五、三角函数与实际问题类型五、三角函数与实际问题 5某乡镇中学教学楼对面是一座小山，去年
17、“联通”公司在山顶上建了座通讯铁塔甲、乙两位同 学想测出铁塔的高度，他们用测角器作了如下操作：甲在教学楼顶 A 处测得塔尖 M 的仰角为，塔座 N 的 仰角为；乙在一楼 B 处只能望到塔尖 M，测得仰角为(望不到底座)，他们知道楼高 AB20 m，通过查 表得：tan0.572 3，tan0.2191，tan0.7489，请你根据这几个数据，结合图形推算出铁塔 第 9 页 共 10 页 高度 MN 的值 【答案与解析】 如图所示，设地平线 BD、水平线 AE 分别交直线 MN 于 D、E，显然 AEBD，不妨设为 m， 则在 RtAEM 中，MEmtan， 在 RtAEN 中，NEmtan M
18、Nm(tantan) 在 RtBDM 中，MDmtan， 而 ABDEMDMEm(tantan)， tantan AB m ， (tantan) tantan AB MN 将 AB20(m)，tan0.5723，tan0.2191，tan0.7489 代入得 MN40(m) 可测得铁塔的高度 MN40m. 【总结升华】构造直角三角形，把实际问题转化为解直角三角形问题. 6如图所示，帆船 A 和帆船 B 在太湖湖面上训练，O 为湖面上的一个定点，教练船静候于 O 点训 练时要求 A，B 两船始终关于 O 点对称以 O 为原点，建立如图所示的坐标系，x 轴，y 轴的正方向分别表 示正东、正北方向设
19、 A，B 两船可近似看成在双曲线 4 y x 上运动湖面风平浪静，双帆远影优美训 练中当教练船与 A，B 两船恰好在直线 yx 上时，三船同时发现湖面上有一遇险的 C 船，此时教练船测得 C 船在东南 45方向上，A 船测得 AC 与 AB 的夹角为 60，B 船也同时测得 C 船的位置(假设 C 船位置不再 改变，A，B，C 三船可分别用 A，B，C 三点表示) (1)发现 C 船时， A， B， C 三船所在位置的坐标分别为 A(_， _)， B(_， _) 和 C(_，_)； (2)发现 C 船，三船立即停止训练，并分别从 A，O，B 三点出发沿最短路线同时前往救援，设 A，B 两 船的
20、速度相等，教练船与 A 船的速度之比为 3:4，问教练船是否最先赶到?请说明理由 【思路点拨】 第 10 页 共 10 页 作 ADx 轴，在等腰直角三角形 ADO 中 结合点 A 在 4 y x 上，不难求出 A 点坐标，而 B 与 A 关于原点对称注意到ABC 为等边三角形，连 OC，作 CHx 轴解直角三角形，求出 CH、OH 的 长，即可求出点 C 坐标在求点 A、B、C 坐标过程中，可求出 AC、OC 的长再根据两船速度比， 分别用含字母的式子表示所用的时间，再比较大小 【答案与解析】 (1)A(2，2)；B(-2，-2)；C(2 3，2 3) (2)作 ADx 轴于 D，连接 AC
21、，BC 和 OC如图所示 A 的坐标为(2，2)， AOD45，AO2 2 C 在 O 的东南 45方向上， AOC45+4590 AOBO， ACBC又 BAC60 ABC 为正三角形， ACBCAB2AO4 2 OCBCcos30 3 4 22 6 2 由条件设：教练船的速度为 3m，A、B 两船的速度均为 4m 则教练船所用的时间为： 2 6 3m ，A、B 两船所用的时间均为 4 22 4mm 教练船不是最先赶到 【总结升华】 （1）一是通过问题提供的信息，知道变量之间有什么函数关系，在这种情况下，可先设出函 数的表达式，再由已知条件确定表达式中的字母系数即可； （2）从问题本身的条件中不知道变量 之间是什么函数关系，在这种情况下和列方程解实际问题一样找出等量关系，把变量联系起来就 得到函数的表达式.
