1、 第 1 页 共 6 页 角角（提高提高）巩固练习巩固练习 【巩固练习】【巩固练习】 一、选择题一、选择题 1关于平角、周角的说法正确的是( ) A平角是一条直线. B周角是一条射线 C反向延长射线 OA，就成一个平角 D两个锐角的和不一定小于平角 2在时刻 215 时，时钟上的时针与分针间的夹角是 （ ） A22.5 B85 C75 D60 3 如图所示， 将一幅三角板叠在一起， 使直角的顶点重合于点 O， 则AOB+DOC 的值 （ ） A小于 180 B等于 180 C大于 180 D不能确定 4如图，是由四个 1 1 的小正方形组成的大正方形，则1+2+3+4（ ） A180 B150
2、 C135 D120 5. 如图，OB、OC 是AOD 的任意两条射线，OM 平分AOB，ON 平分COD，若 MON，BOC，则表示AOD 的式子是 （ ） A2 B C D以上都不正确 6如图将长方形纸片 ABCD 的角 C 沿着 GF 折叠（点 F 在 BC 上，不与 B、C 重合） ，使得点 C 落在长方形内部点 E 处， 若 FH 平分BFE， 则关于GFH 的度数说法正确的是 （ ） A 90180 B 090 C 90 D随折痕 GF 位置的变化而变化 二、填空题二、填空题 A B C D G E F H 第 2 页 共 6 页 7书店、学校、食堂在同一个平面上，分别用点 A、B
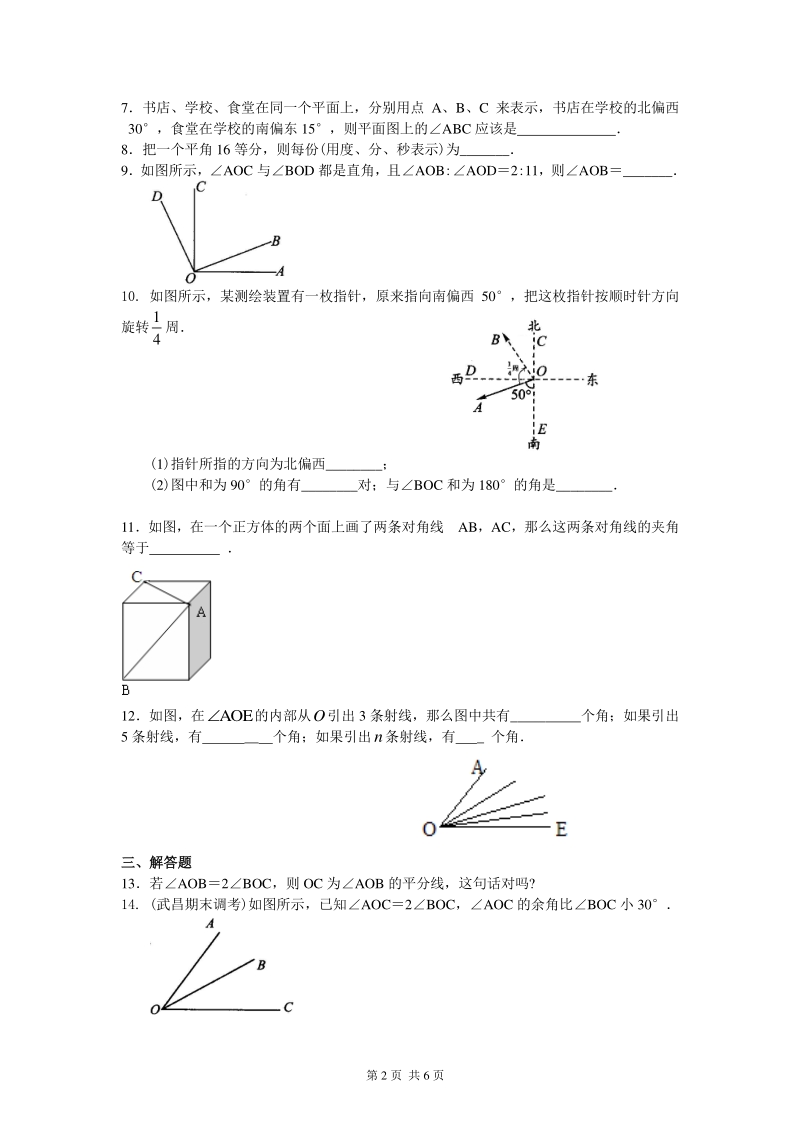
3、、C 来表示，书店在学校的北偏西 30，食堂在学校的南偏东 15，则平面图上的ABC 应该是 8把一个平角 16 等分，则每份(用度、分、秒表示)为_ 9如图所示，AOC 与BOD 都是直角，且AOB:AOD2:11，则AOB_ 10. 如图所示，某测绘装置有一枚指针，原来指向南偏西 50，把这枚指针按顺时针方向 旋转 1 4 周 (1)指针所指的方向为北偏西_； (2)图中和为 90的角有_对；与BOC 和为 180的角是_ 11如图，在一个正方体的两个面上画了两条对角线 AB，AC，那么这两条对角线的夹角 等于 12如图，在AOE的内部从O引出 3 条射线，那么图中共有_个角；如果引出 5
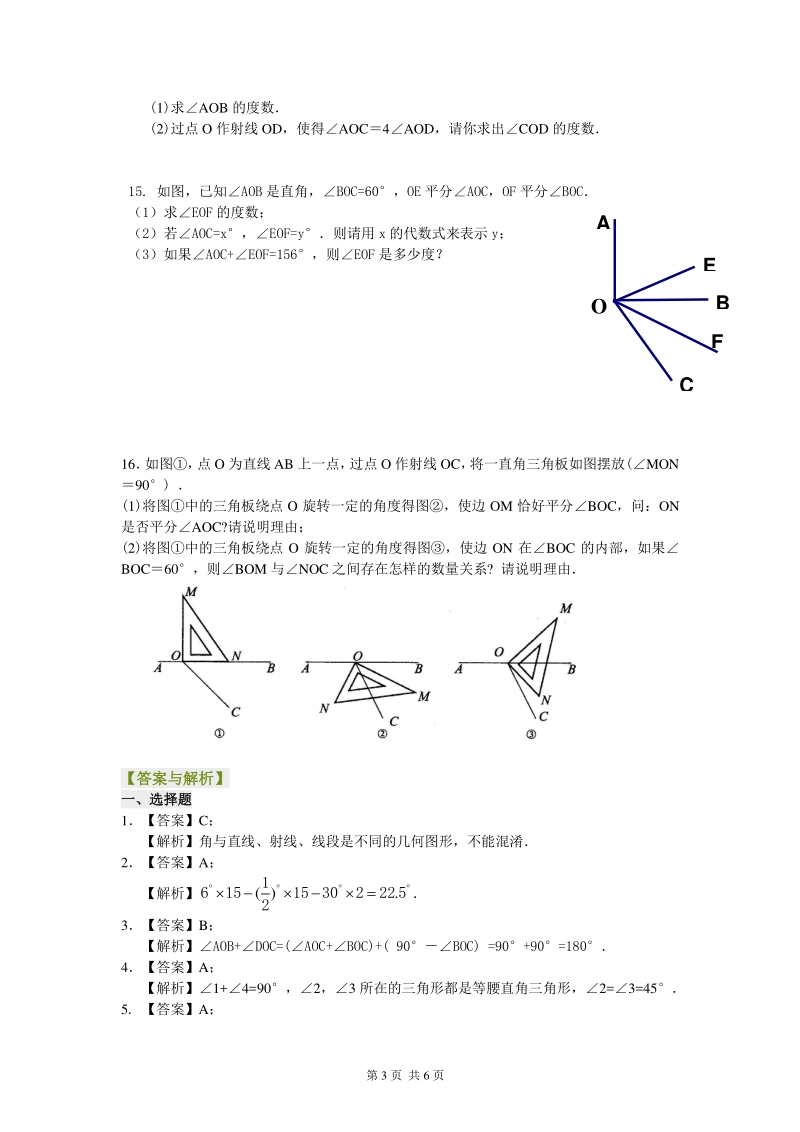
4、 条射线，有 _ 个角；如果引出n条射线，有 _ 个角 三、三、解答题解答题 13若AOB2BOC，则 OC 为AOB 的平分线，这句话对吗? 14. (武昌期末调考)如图所示，已知AOC2BOC，AOC 的余角比BOC 小 30 第 3 页 共 6 页 (1)求AOB 的度数 (2)过点 O 作射线 OD，使得AOC4AOD，请你求出COD 的度数 15. 如图，已知AOB 是直角，BOC=60，OE 平分AOC，OF 平分BOC （1）求EOF 的度数； （2）若AOC=x，EOF=y则请用 x 的代数式来表示 y； （3）如果AOC+EOF=156，则EOF 是多少度？ 16 如图， 点
5、 O 为直线 AB 上一点， 过点 O 作射线 OC， 将一直角三角板如图摆放(MON 90) (1)将图中的三角板绕点 O 旋转一定的角度得图，使边 OM 恰好平分BOC，问：ON 是否平分AOC?请说明理由； (2)将图中的三角板绕点 O 旋转一定的角度得图，使边 ON 在BOC 的内部，如果 BOC60，则BOM 与NOC 之间存在怎样的数量关系? 请说明理由 【答案与解析答案与解析】 一、选择题一、选择题 1【答案】C； 【解析】角与直线、射线、线段是不同的几何图形，不能混淆 2【答案】A； 【解析】( ). 1 61515302225 2 3【答案】B； 【解析】AOB+DOC=(A
6、OC+BOC)+( 90BOC) =90+90=180 4【答案】A； 【解析】1+4=90，2，3 所在的三角形都是等腰直角三角形，2=3=45 5. 【答案】A； O B C E A F 第 4 页 共 6 页 6【答案】C； 【解析】COG=EFG, EFH=HFB, 2(EFG+EFH) =180,所以EFG+EFH=90， 即GFH=90 二、填空题二、填空题 7. 【答案】165； 【解析】如图所示 8. 【答案】1115； 【解析】度、分、秒的换算为“六十进制” ，上一级的余数乘以 60，变换到下一级再运算 9.【答案】20； 【解析】设AOB2x，则AOD11x，DOC2x，所
7、以BOC7x，所以 2x+7x 90，x10，AOB2x20 10.【答案】(1)40； (2)4 ， BDE； 【解析】如下图， 1 =90 4 周，COB=AOD=40，DOB=AOE=50，图中和为 90的角有 4 对，分别为：COB 与DOB，COB 与AOE,DOB 与AOD, AOD 与AOE. 11.【答案】60； 【解析】连接 BC，可得：ABC 为等边三角形 12.【答案】10, 21， (1)(2) 2 nn ； 【解析】 在AOE的内部从O引出 3 条射线， 则图中共有角的个数：4 3 2 1 10 ； 如果引出 5 条射线，则图中共有角的个数：6 5 4 3 2 121
8、 ； 如果引出n条射线，则图中共有角的个数： (1)(2) (1)(1). 1 2 nn nnn 三、解答题三、解答题 13.【解析】 解：不正确，应改为：若AOB2BOC2AOC,那么 OC 为AOB 的平分线，或改为 若AOB2BOC，且 OC 在AOB 的内部，则 OC 为AOB 的平分线 错误在于没有理解好角平分线的定义，而由AOB2BOC 能画出两种情况如图所 第 5 页 共 6 页 示，但(1)中 OC 不是AOB 的平分线，而(2)中 OC 为AOB 的平分线 (2) 14【解析】 解：(1)设BOCx则AOC2x 依题意列方程：90-2xx-30， 解得：3x120 x40 A
9、OBAOCBOC2x- x= 40 (2)由(1)有：AOC=2x80， 当射线 OD 在AOC 的内部时， AOC4AOD， AOD 1 4 AOC20 CODAOC-AOD60 当射线 OD 在AOC 的外部时，CODAOD+AOC 1 4 AOC+AOC 20+80100 15.【解析】 解： （1）AOB 是直角，BOC=60， AOC=AOB+BOC=90+60=150， OE 平分AOC，OF 平分BOC， EOC= 1 2 AOC= 1 2 150=75，COF= 1 2 BOC=30， EOF=EOC-COF=75-30=45； （2）AOB 是直角，AOC=x， BOC=AO
10、C-AOB=x-90， OE 平分AOC，OF 平分BOC， EOC= 1 2 AOC= 1 2 x，COF= 1 2 BOC= 1 2 （x-90） ， EOF=EOC-COF= 1 2 x- 1 2 （x-90）=45； （3）根据（2）的规律发现，EOF 的度数只与AOB 有关， EOF= 1 2 AOB= 1 2 90=45 16. 【解析】 解：(1)ON 平分AOC理由如下： MON90 BOM+AON90 第 6 页 共 6 页 MOC+NOC90 又 OM 平分BOC BOMMOC AONNOC ON 平分AOC (2) CON+NOB60 又 BOM+NOB90 BOMNOC+30
