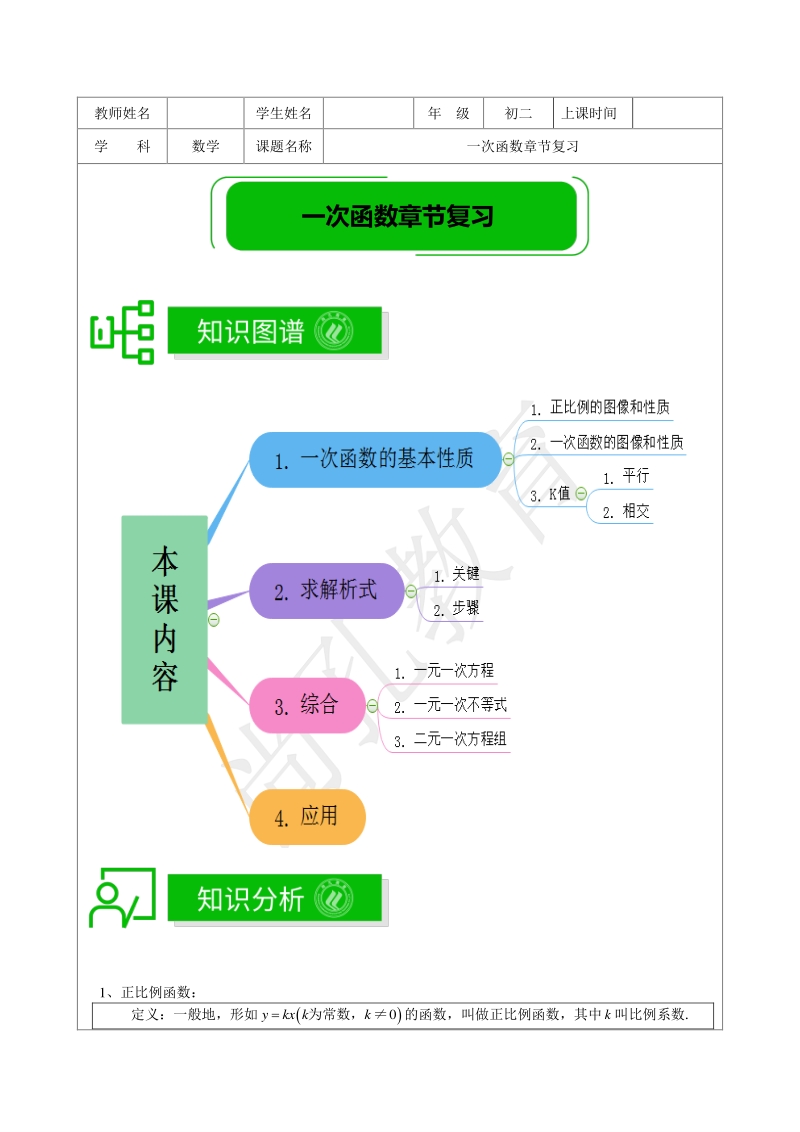
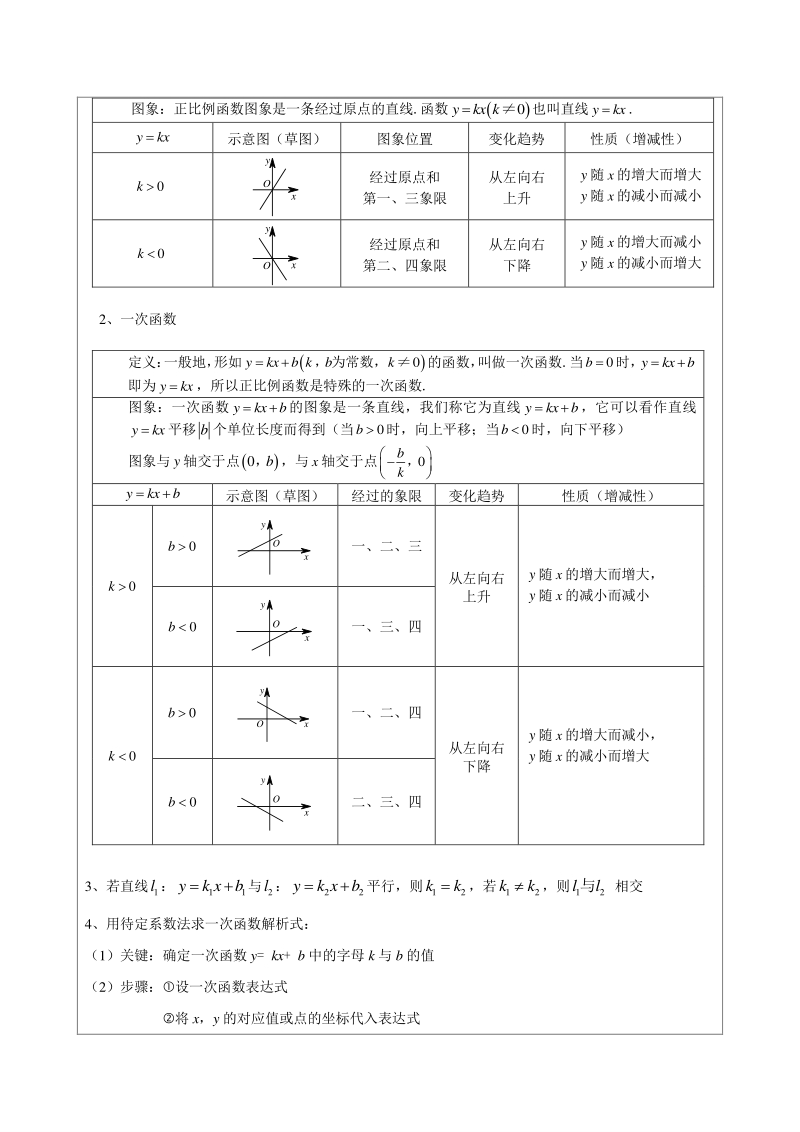
1、教师姓名 学生姓名 年 级 初二 上课时间 学 科 数学 课题名称 一次函数章节复习 1、正比例函数： 定义：一般地，形如0ykx kk为常数， 的函数，叫做正比例函数，其中k叫比例系数. 一次函数章节复习 图象：正比例函数图象是一条经过原点的直线.函数0ykx k也叫直线ykx. ykx 示意图（草图） 图象位置 变化趋势 性质（增减性） 0k 经过原点和 第一、三象限 从左向右 上升 y随x的增大而增大 y随x的减小而减小 0k 经过原点和 第二、四象限 从左向右 下降 y随x的增大而减小 y随x的减小而增大 2、一次函数 定义： 一般地， 形如0ykxb kbk，为常数， 的函数， 叫做
2、一次函数.当0b 时，ykxb 即为ykx，所以正比例函数是特殊的一次函数. 图象：一次函数ykxb的图象是一条直线，我们称它为直线ykxb，它可以看作直线 ykx平移b个单位长度而得到（当0b 时，向上平移；当0b 时，向下平移） 图象与y轴交于点0 b，与x轴交于点0 b k ， ykxb 示意图（草图） 经过的象限 变化趋势 性质（增减性） 0k 0b 一、二、三 从左向右 上升 y随x的增大而增大， y随x的减小而减小 0b 一、三、四 0k 0b 一、二、四 从左向右 下降 y随x的增大而减小， y随x的减小而增大 0b 二、三、四 3、若直线 1 l： 11 yk xb与 2 l：
3、 22 yk xb平行，则 12 kk，若 12 kk，则 12 ll与 相交 4、用待定系数法求一次函数解析式： （1）关键：确定一次函数 y= kx+ b 中的字母 k 与 b 的值 （2）步骤：设一次函数表达式 将 x，y 的对应值或点的坐标代入表达式 O y x x y O O y x O y x x y O O y x 解关于系数的方程或方程组 将所求的待定系数代入所设函数表达式中 5、一次函数与一元一次方程、一元一次不等式和二元一次方程组 （1）一次函数与一元一次方程：求直线与坐标轴的交点坐标。 （2）一次函数与一元一次不等式：kx+ b0 或 kx+ b0 即一次函数图象位于 x
4、 轴上方或下方时相应的 x 的取值范围，反之也成立 （3） 一次函数与二元一次方程组： 两条直线的交点坐标即为两个一次函数所列二元一次方程组的解， 反之根据方程组的解可求两条直线的交点坐标 6、一次函数的应用 一般步骤： （1）设定问题中的变量 （2）建立一次函数关系式 （3）确定自变量的取值范围 （4）利用函数性质解决问题 （5）作答 【例 1】若k、b是一元二次方程 2 0xpxq的两个实根（0kb ），在一次函数ykxb中，y随 x的增大而减小，则一次函数的图像一定经过（ ） A、第一、二、四象限 B、第一、二、三象限 C、第二、三、四象限 D、第一、三、四象限 【答案】A 【例 2】已
5、知一次函数ykxb（0k ） ，把它的图像向右平移 3 个单位，再向下平移 5 个单位，所得 到的图像与原来的图像重合，则k=_ 【答案】 5 3 【例 3】如图所示，一次函数与反比例函数的图象分别是直线 AB 和双曲线。直线 AB 与双曲线的一个 交点为 C，CD 垂直 x 轴于点 D，OD=2OB=4OA=4。求一次函数和反比例函数的解析式. O B A x y 【答案】一次函数的解析式：； 反比例函数的解析式为： 【例 4】 如图，直线ykxb与坐标轴交于 A（3，0） ，B（0，5）两点， 则不等式0kxb的解集为_. 如图，已知直线yaxb与直线yxc的交点的横坐标为 1， 根据图象
6、有下列四个结论： 0a ； 0c ； 对于直线yxc上任意两点 AA A xy，、 BB B xy，若 AB xx，则 AB yy； 1x 是不等式axbxc的解集 其中正确的结论是（ ） A B C D 如图，直线ykxb经过2 112AB ， ，两点，则不等式 1 2 2 xkxb 的解集为_ 【答案】 3x C 12x ，此题要求学生补上 1 2 yx的图象，然后利用图象法来解不等式，这样才能体现 一种函数思想. 当然，也可以用待定系数法求解析式，然后解不等式组，但是较为麻烦. 【例 5】已知一次函数的函数值随的增大而增大，求的值及解析式 【答案】3m ，6yx 1 1 2 yx 4 y
7、 x 2 57 (25)2 mm ymxm yxm C DB A x O y 1 y=ax+b y=x+c O y x 【例 6】如图，已知一次函数的图像交轴于 A（6，0） ，交正比例函数的图像于点 B，且点 B 在第三 象限，它的横坐标为，AOB 的面积为 6，求正比例函数和一次函数的解析式 【答案】y x ， 1 3 2 yx 【例 7】在一次运输任务中，一辆汽车将一批货物从甲地运往乙地，到达乙地卸货后返回设汽车从甲 地出发 x(h)时，汽车与甲地的距离为 y(km)，y 与 x 的函数关系如图所示 根据图像信息，解答下列问题： （1）这辆汽车的往、返速度是否相同？请说明理由； （2）求
8、返程中 y 与 x 之间的函数表达式； （3）求这辆汽车从甲地出发 4h 时与甲地的距离 【答案】（1）不同，往、返速度分别为 60km/h、48km/h；（2）48240yx ； （3）48km 【例 8】A 市和 B 市分别有某种库存机器 12 台和 6 台,现决定支援 C 村 10 台，D 村 8 台，已知从 A 市 调运一台机器到 C 村和 D 村的运费分别是 400 元和 800 元， 从 B 市调运一台机器到 C 村和 D 村的运费 分别是 300 元和 500 元 （1）设 B 市运往 C 村机器 x 台，求总运费 W 关于 x 的函数关系式； （2）若要求总运费不超过 9000
9、 元，共有几种调运方案? x 2 120 52.520 x/h y/km A B O D x y （3）求出总运费最低的调运方案，最低运费是多少元? 【答案】（1）2008600Wx； （2）3 种，x=0、1、2 时第一种：A 市往 C 村、D 村分别支 援 10 台、2 台，B 市往 C 村、D 村分别支援 0 台、6 台；第二种：A 市往 C 村、D 村分别 支援 9 台、3 台，B 市往 C 村、D 村分别支援 1 台、5 台；第三种：A 市往 C 村、D 村分别 支援 8 台、4 台，B 市往 C 村、D 村分别支援 2 台、4 台； （3）x=0 时，总运费最低，W=8600 元，
10、调运方案为：A 市往 C 村、D 村分别支援 10 台、 2 台，B 市往 D 村支援 6 台 【例 9】如图，直线 L： 1 2 2 yx 与 x 轴、y 轴分别交于 A、B 两点，在 y 轴上有一点 C（0，4） ，动点 M 从 A 点以每秒 1 个单位的速度沿 x 轴向左移动 （1）求 A、B 两点的坐标； （2）求COM 的面积 S 与 M 的移动时间 t 之间的函数关系式； （3）当 t 何值时COMAOB，并求此时 M 点的坐标 【答案】（1）A（4，0） 、B（0，2） ； （2） 82 04 284 tt S tt ； （3） 1 t=2， 1 M（2，0） ， 2 t=6，
11、2 M（-2，0） 【习题 1】下列图像中，不可能是关于x的一次函数3ymxm的图像的是（ ） 【答案】C 【习题 2】如图中的图象（折线 OBCDE）描述了一汽车在某一直线上的行驶过程中，汽车离出发地的 距离 s（千米）和行驶时间 t（小时）之间的函数关系，根据图中提供的信息，给出 下列说法：汽车 共行驶了 120 千米；汽车在行驶途中停留了 0.5 小时；汽车在整个行驶过程中的平均速度为千 米/时；汽车自出发后 3 小时至 4.5 小时之间行驶的速度在逐渐减少.其中正确的说法共有（ ） A1 个 B2 个 C3 个 D4 个 【答案】 A 【习题 3】“龟兔赛跑”讲述了这样的故事；领先的兔
12、子看着缓慢爬行的乌龟，骄傲起来，睡了一觉， 当它醒来时，发现乌龟快爬到终点了，于是急忙追赶，但为时已晚，乌龟先到达了终点用 S1、S2分别 表示乌龟和兔子所行的路程，t 为时间，则下列图象中与故事相吻和的是（ ） 【答案】 D 【习题 4】下列语句不正确的是（ ） A所有的正比例函数都是一次函数 B一次函数的一般形式是 C正比例函数和一次函数的图象都是直线 D正比例函数的图象是一条过原点的直线 【答案】 B x y x y x y x y DC B A OOO O 80 3 ykxb 3 120 80 4.521.50 s（千米） B C D E t（小时） O s t S1 S2 O s t
13、 S1 S2 O s t S1 S2 O s t S1 S2 A B C D 【习题 5】已知一次函数618yx . （1）如果1x ，求y的取值范围 （2）如果224y，求x的取值范围 （3）在平面直角坐标系中，在直线618yx 上且位于x轴下方的所有点，他们的横坐标的取值范 围是什么？ 【答案】 （1）12y （2） 8 1 3 x （3）3x 【习题 6】已知直线l过点2, 4 ，且与坐标轴围城一个等腰三角形. （1）求该直线的函数解析式 （2）求所得三角形的周长 C 及面积 S. 【答案】 （1）6yx或2yx （2） 周长：4+2 2 面积：2 或 周长：12+6 2 面积：18 【
14、习题 7】已知平面上一动点 P（x，y）从 M（-1，0）出发，沿 A（-1，1） 、B（1，1） 、 C（1，-1） 、D（-1，-1）四点组成的正方形边线如图 1 按一定方向运动，图 2 是点 P 点运动的路 程 s（个单位）与运动时间 t（秒）之间的函数图像，图 3 是点 P 的纵坐标 y 与 P 点运动的路程 s 之间的函数图像的一部分 （1）求 s 与 t 之间的函数关系式? （2） 与图 3 相对应的 P 的运动路径是_； P 点出发_秒首次到达 B 点 1 0 4 3 210 1 2 A B C D N M O P x y t s y s 图 1 图 2 图 3 【答案】（1）
15、1 2 st； （2）MABN，6 【习题 8】已知一次函数 （1）求证：无论取何实数，函数的图像恒过一点； （2）当在 12 内变化时，在5 内变化，求的值 【答案】（1）略；（2）m=3 【习题 9】如图所示，一次函数与反比例函数在第一象限的图像交于点 B，且点 B 的横 坐标为 1，过点 B 作轴的垂线，点 C 为垂足，若，求一次函数和反比例函数的解析式 【答案】2yx， 3 y x (2)23ymxm m xxy4ym yxb k y x y 3 2 BCO S A B C O x y 【习题 10】中学预计用 1500 元购买甲商品个，乙商品个，不料甲商品单价上涨 1.5 元，乙商品单 价上涨 1 元，尽管购买甲商品的个数比预定减少 10 个，总金额还是多了 29 元又若甲、乙商品单价上 涨 1 元，并且购买甲商品的数量只比预定数少 5 个，那么买甲、乙两商品支付的总金额是 1563.5 元 （1）求、的关系式； （2）若预计购买甲商品的个数的 2 倍与预计购买乙商品的个数的和大于 205，但小于 210， 求、的值 【答案】（1）2186xy； （2）x =76，y =55 xy xy xy
