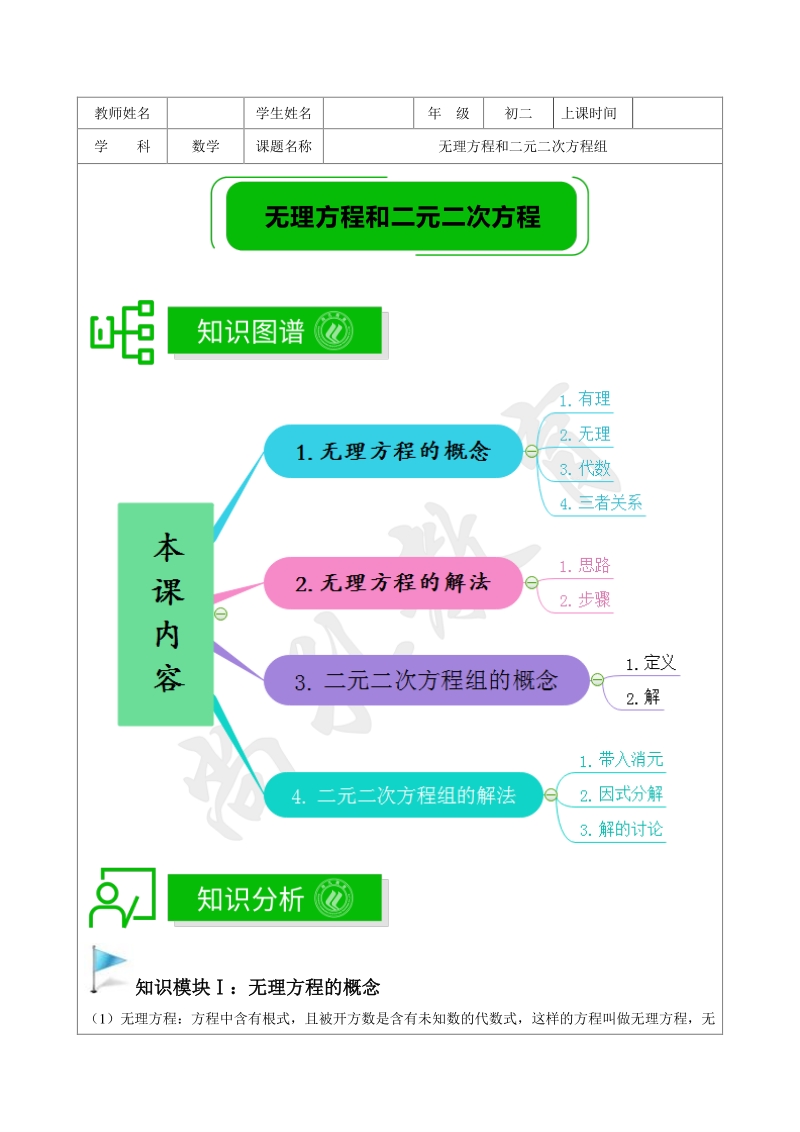
1、教师姓名 学生姓名 年 级 初二 上课时间 学 科 数学 课题名称 无理方程和二元二次方程组 知识模块：无理方程的概念知识模块：无理方程的概念 （1）无理方程：方程中含有根式，且被开方数是含有未知数的代数式，这样的方程叫做无理方程，无 无理方程和二元二次方程 理方程也叫根式方程。 （2）有理方程：整式方程和分式方程统称为有理方程. （3）代数方程：有理方程和无理方程统称为代数方程. （4）无理方程、有理方程和代数方程三者的关系： 代数方程 无理方程 分式方程 整式方程 有理方程 【例 1】在方程（1）0xx， （2）120x （3） 2 3270xx （4） 2 30 1 x x （5） 3
2、2 11 x xx （6） 12 0 5 x x 中， 是无理方程的是_ 【答案】 （1） （2） （4） 【例 2】下列方程有无实数根?并说明理由 （1）20x ； （2）47xx； （3）7241xx； （4）52251xx 【答案】（1）0x ，所以22x ，所以20x 无实数根； （2）由被开方数的意义知40x，得4x ，又因为等号左边0，所以等号右边0， 即70x ，得7x 与4x 冲突，所以方程无实数根； （3）由被开方数的意义知720,40xx由720x，得 7 2 x ；由40x 得4x 两者冲突，所以方程无实数根； （4）由被开方数的意义知520250xx且，所以只有520x
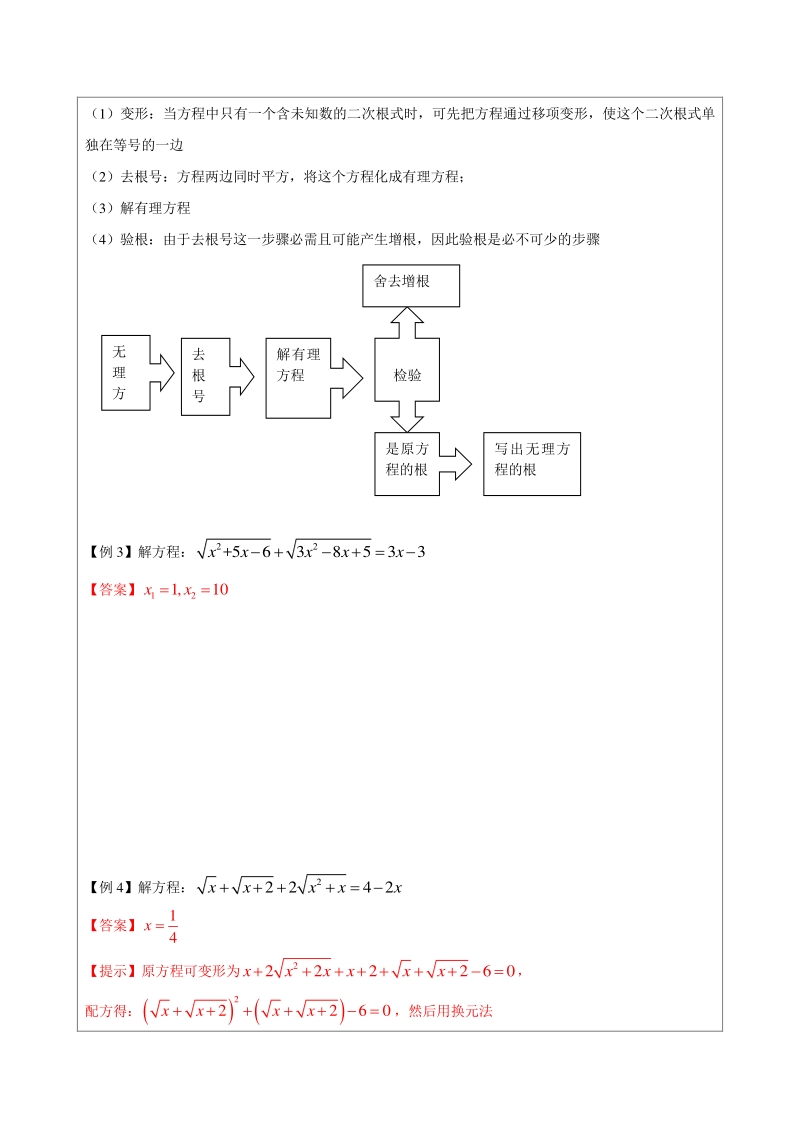
3、 即 5 2 x 等号的左边=0+0右边=1，所以方程无实数解 知识模块：无理方程的解法知识模块：无理方程的解法 1、解无理方程的基本思路：解简单的无理方程，可以通过去根号转化为有理方程来解。 2、解简单的无理方程的一般步骤： （1）变形：当方程中只有一个含未知数的二次根式时，可先把方程通过移项变形，使这个二次根式单 独在等号的一边 （2）去根号：方程两边同时平方，将这个方程化成有理方程； （3）解有理方程 （4）验根：由于去根号这一步骤必需且可能产生增根，因此验根是必不可少的步骤 【例 3】解方程： 22 +5638533xxxxx 【答案】 12 1,10xx 【例 4】解方程： 2 22
4、42xxxxx 【答案】 1 4 x 【提示】原方程可变形为 2 222260xxxxxx ， 配方得： 2 2260xxxx，然后用换元法 无 理 方 去 根 号 解有理 方程 检验 舍去增根 是原方 程的根 写出无理方 程的根 【例 5】 11 1xx xx 【答案】 15 2 x 【提示】设 22 11 ,1,0,1axbabxabx xx 则 两式相除得 1 1ab x ，因此 2 1 211axa x ，则 2 10,1aa解得： 即 1 1x x ，解方程得 15 2 x （负值舍去） 【例 6】若关于 x 的无理方程022-4kxx有实数根，求 k 的取值范围. 【答案】10kk
5、或 知识模块：二元二次方程（组）知识模块：二元二次方程（组） 1、 定义：仅含有两个未知数，并且含有未知数的项的最高次数是 2 的整式方程所组成的方程组叫做二 元二次方程组。 2、 二元二次方程组的解：二元二次方程组，所含各方程的公共解叫做二元二次方程组的解。 【例 7】下列方程中哪些是二元二次方程组? （1） 5 1 xy xy ； （2） 12 0 61 8 xy xy ； （3） 22 1 1 xy xxyy ； （4） 3 1 2 xy xyyx 【答案】（3） 【例 8】已知 0 3 x y ，与 1 7 x y ，是关于 x、y 的二元二次方程 2 30axby的两组解，试求ab的
6、 值。 【答案】1 或-3 知识模块：二元二次方程组的解法知识模块：二元二次方程组的解法 （一）代入消元法解二元二次方程组 1、解二元二次方程组的基本思想是消元和降次 2、用代入消元法解二元二次方程组的一般步骤 （1）将方程组中二元一次方程的一个未知数用另一个未知数的代数式表示； （2）将这个未知数所表示的代数式代入方程组中的二元二次方程，得到关于另一个未知数 的一元二次方程 3、 解这个一元二次方程 4、将求得的两个解分别代入二元一次方程，求出相应的另一个未知数的值； （二）因式分解法解二元二次方程组 解形如（或可转化为） 22 0 +0 AxByCxDyABCD axbycxydx eya
7、bcdeabc 、 、 、 为常数且不同时为零 、 、 、 、 为常数，且 、 、 不同时为零 的二元二次方程组的基本解题思路：利用方程的特点“降次” ，把原方程组化归为由一个二元一次方 程与一个二元二次方程所组成的方程组。 （三）二元二次方程组的解的讨论 【例 9】解方程组： 22 22 7 3 xxyy xxyy 【答案】 1 1 2 1 x y ， 2 2 1 2 x y ， 3 3 1 2 x y ， 4 4 2 1 x y 【例 10】 2 2 210 3630 xxyxy xyyxy 【答案】 1 1 1 1 x y ， 2 2 517 4 153 17 4 x y ， 3 3 5
8、17 4 153 17 4 x y 【例 11】当a取哪些值时，方程组 22 2 2(1) (xy)14 xya 只有两组实数解？ 【答案】 5 2 a 【提示】若 o o xy yx ，则 o o xy yx ， o o xy yx 也是原方程组的解，要使原方程组有两组实数解，必须 使 oo xy或 oo xy 【例 12】已知方程组 2 (21)40 2 xky yx （1）求证：不论k为何值时，此方程组一定有实数解； （2）设等腰ABC 的三边长分别为a，b，c，其中4c ，且 2 xa ya ， 2 xb yb 是该方程的 两个解，求ABC 的周长 【答案】（1）将2yx代入 2 21
9、40xky，得 2 21240xkx， 整理得 2 21420xkxk， 22 2 214 1424129230kkkkk ， 所以不论k为何值时，此方程组一定有实数解； （2）可分为两种情况ab，或者4a 第一种情况ab，即方程组有两个相等的实数根，可知0 ，从而 3 2 k ， 由韦达定理得214abk ，此时abc， ，不能构成三角形，舍去； 第二种情况4a ，将4x 代入 2 21420xkxk，得 5 2 k ， 由韦达定理得216abk ，可得：2b ，此时abc， ，能构成三角形， 故周长=4+4+2=10 【习题 1】不解方程，是说明下列方程为什么无实数根？ （1）21 10x
10、 （2） 325xx （3） 57xx （4）210yy 【答案】略 【习题 2】解下方程： （1）23xx （2）1263xxx 【答案】 （1）3x （2）5x 【习题 3】解方程：2116xxx 【答案】5x 【习题 4】解方程： 2 2214xxx x 【答案】2x 【习题 5】解下列方程： （1） 22 25 26xxxx （2） 2 2513 (x 5)2xxx 【答案】 （1） 12 1 ,1 2 xx （2） 12 0,5xx 【习题 6】解方程： 22 1 1 xy xxyy 【答案】 1 1 1 6 x y ， 2 2 6 1 x y ， 3 3 43 43 x y ， 4 4 43 43 x y 【习题 7】解方程组： 3 38 xxy xyy 【答案】 1 1 1 2 x y ， 2 2 1 4 x y 【习题 8】解方程： 22 22 +449 440 xxyy xyxy 【答案】 1 1 1 1 x y ， 2 2 5 1 x y ， 3 3 1 1 x y ， 4 4 11 7 x y 【习题 9】当k为何值时，方程组 22 4 2 2 xy ykx 有唯一的一组实数解？ 【答案】1k 【习题 10】当取什么值时,方程组有两个相同的实数解?并求出此时方程组的解 【答案】 3 2 m ； 12 12 1 5 2 xx yy m 2 24 xym xy
