1、 第 1 页（共 26 页） 2018 年湖南省长沙市岳麓区麓山国际实验学校中考数学一模试年湖南省长沙市岳麓区麓山国际实验学校中考数学一模试 卷卷 一、选择题（本大题共一、选择题（本大题共 12 小题，每小题小题，每小题 3 分，共分，共 36 分）分） 1 （3 分）|6|的值是（ ） A6 B6 C D 2 （3 分）如图，在数轴上点 M 表示的数可能是（ ） A1.5 B1.5 C2.4 D2.4 3 （3 分）下列二次根式中，能与合并的是（ ） A B C D 4 （3 分）如果一组数据 1，2，x，5，6 的众数为 6，则这组数据的中位数为（ ） A1 B2 C5 D6 5 （3 分
2、）二次函数 y（x2）2+7 的顶点坐标是（ ） A （2，7） B （2，7） C （2，7） D （2，7） 6 （3 分）下列说法正确的是（ ） A面积相等的两个三角形一定全等 B平分弦的直径垂直于弦 C矩形的对角线互相平分且相等 D对角线互相垂直的四边形是菱形 7 （3 分）若一个等腰三角形的两边长分别为 2 和 4，则这个等腰三角形的周长是为（ ） A8 B10 C8 或 10 D6 或 12 8 （3 分）正多边形的一个内角为 135，则该多边形的边数为（ ） A5 B6 C7 D8 9 （3 分） 如图， 一座石拱桥是圆弧形其跨度 AB24 米， 半径为 13 米， 则拱高 CD
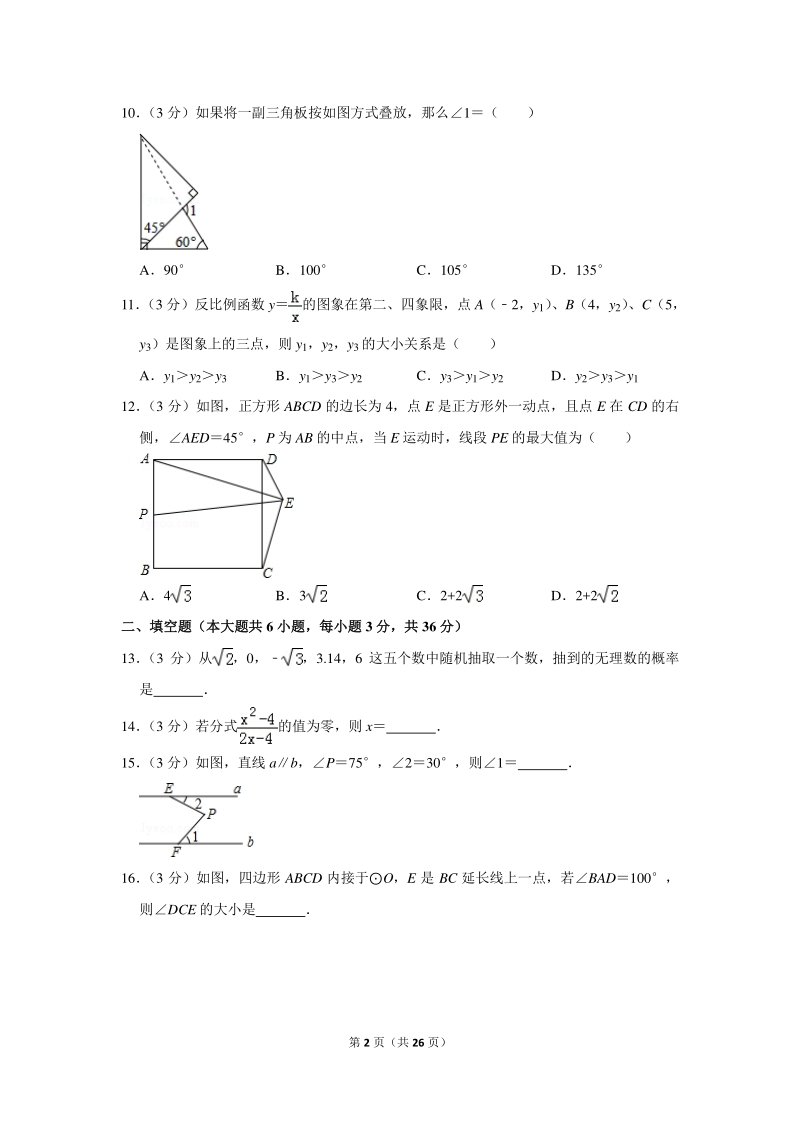
3、 为 （ ） A3米 B5 米 C7 米 D8 米 第 2 页（共 26 页） 10 （3 分）如果将一副三角板按如图方式叠放，那么1（ ） A90 B100 C105 D135 11 （3 分）反比例函数 y的图象在第二、四象限，点 A（2，y1） 、B（4，y2） 、C（5， y3）是图象上的三点，则 y1，y2，y3的大小关系是（ ） Ay1y2y3 By1y3y2 Cy3y1y2 Dy2y3y1 12 （3 分）如图，正方形 ABCD 的边长为 4，点 E 是正方形外一动点，且点 E 在 CD 的右 侧，AED45，P 为 AB 的中点，当 E 运动时，线段 PE 的最大值为（ ） A
4、4 B3 C2+2 D2+2 二、填空题（本大题共二、填空题（本大题共 6 小题，每小题小题，每小题 3 分，共分，共 36 分）分） 13 （3 分）从，0，3.14，6 这五个数中随机抽取一个数，抽到的无理数的概率 是 14 （3 分）若分式的值为零，则 x 15 （3 分）如图，直线 ab，P75，230，则1 16 （3 分）如图，四边形 ABCD 内接于O，E 是 BC 延长线上一点，若BAD100， 则DCE 的大小是 第 3 页（共 26 页） 17 （3 分）若圆锥的底面积为 16cm2，母线长为 12cm，则它的侧面展开图的圆心角 为 18 （3 分）若关于 x 的一元二次方
5、程 kx26x+90 有两个不相等的实数根，则 k 的取值范 围 三、解答题（本大题共三、解答题（本大题共 8 小题，共小题，共 66 分）分） 19 （6 分）计算：22+（2018）02sin60+|1| 20 （6 分）已知 xy，求代数式（x+1）22x+y（y2x）的值 21 （8 分）长沙市文化底蕴深厚，旅游资源丰富，天心阁、岳麓山、橘子洲三个景区是人 们节假日游玩的热点景区，李老师对九年级 1 班学生五一长假随父母到这三个景区游玩 的计划做了全面调查，调查分四个类别：A、游三个景区；B、游两个景区；C、游一个 景区；D、不到这三个景区游玩现根据调查结果绘制了不完整的条形统计图和扇
6、形统计 图，请结合图中信息解答下列问题： （1）九（1）班共有学生 人，请将条形统计图补充完整； （2）在扇形统计图中，表示“B 类别”的扇形的圆心角的度数为 ； （3）若小明、小华两名同学，各自从三个景区中随机选一个作为 5 月 1 日游玩的景区， 请用列表或者画树状图的形式求出他们同时选中岳麓山的概率 22 （8 分）如图，某公安海上缉私局发现在我国领海的 P 处有一条走私船正以 22 海里/时 的速度沿南偏东 64的方向向公海逃窜，于是缉私局命令位于点 P 北偏东 30方向 A 处的我公安缉私快艇前往拦截，已知 P、A 相距 20 海里，公安缉私快艇向正南方向行进 第 4 页（共 26
7、页） 计划在 B 处拦截走私船 （1）求 A、B 两处的距离； （结果保留整数） （2） 若公安缉私快艇要在 B 处成功拦截走私船， 则缉私快艇的速度至少为多少海里/时？ 【参考数据： sin640.90， cos640.44， tan642，1.4，】 23 （9 分） “低碳生活，绿色出行” ，共享单车已经成了很多人出行的主要选择，今年 1 月 份， “摩拜”共享单车又向长沙河西新投放共享单车 640 辆 （1） 若 1月份到 3月份新投放单车数量的月平均增长率相同， 3月份新投放共享单车 1000 辆求月平均增长率 （2）考虑到共享单车市场竞争激烈，摩拜公司准备用不超过 60000 元的
8、资金再购进 A， B 两种规格的自行车 100 辆，且 A 型车不超过 60 辆已知 A 型的进价为 500 元/辆，B 型车进价为 700 元/辆，设购进 A 型车 m 辆，求出 m 的取值范围 （3） 已知 A 型车每月产生的利润是 100 元/辆， B 型车每月产生的利润是 90 元/辆， 在 （2） 的条件下，求公司每月的最大利润 24 （9 分）如图，已知 AO 为 RtABC 的角平分线，ACB90，以 O 为圆心， OC 为半径的圆分别交 AO，BC 于点 D，E，连接 ED 并延长交 AC 于点 F （1）求证：AB 是O 的切线； （2）求 tanCAO 的值 （3）若O 的
9、半径为 4，求的值 第 5 页（共 26 页） 25 （10 分）定义：如图 1，点 M、N 把线段 AB 分割成 AM、MN 和 BN，若以 AM、MN、 BN 为边的三角形是一个直角三角形，则称点 M、N 是线段 AB 的勾股点 （1）已知点 M、N 是线段 AB 的勾股点，若 AM1，MN2，求 BN 的长； （2）如图 2，点 P（a，b）是反比例函数 y（x0）上的动点，直线 yx+2 与坐 标轴分别交于 A、B 两点，过点 P 分别向 x、y 轴作垂线，垂足为 C、D，且交线段 AB 于 E、F证明：E、F 是线段 AB 的勾股点； （3） 如图 3， 已知一次函数 yx+3 与坐
10、标轴交于 A、 B 两点， 与二次函数 yx24x+m 交于 C、D 两点，若 C、D 是线段 AB 的勾股点，求 m 的值 26 （10 分）如图，在平面直角坐标系 xOy 中，将抛物线 yx2的对称轴绕着点 P（0，2） 顺时针旋转 45后与该抛物线交于 A，B 两点，点 Q 是该抛物线上的一点 （1）求 A，B 两点的坐标 （2）如图，若点 Q 在直线 AB 的下方，求点 Q 到直线 AB 的距离的最大值； （3）如图，若点 Q 在 y 轴左侧，且点 T（0，t） （t2）是直线 PO 上一点，当以 P， B，Q 为顶点的三角形与PAT 相似时，求所有满足条件的 t 的值 第 6 页（共
11、 26 页） 2018 年湖南省长沙市岳麓区麓山国际实验学校中考数学年湖南省长沙市岳麓区麓山国际实验学校中考数学 一模试卷一模试卷 参考答案与参考答案与试题解析试题解析 一、选择题（本大题共一、选择题（本大题共 12 小题，每小题小题，每小题 3 分，共分，共 36 分）分） 1 （3 分）|6|的值是（ ） A6 B6 C D 【分析】利用绝对值的定义解答即可 【解答】解：|6|6， 故选：B 【点评】本题主要考查了绝对值的定义，理解定义是解答此题的关键 2 （3 分）如图，在数轴上点 M 表示的数可能是（ ） A1.5 B1.5 C2.4 D2.4 【分析】根据数轴上点 M 的位置，可得点
12、 M 表示的数 【解答】解：点 M 表示的数大于3 且小于2， A、1.52，故 A 错误； B、1.52，故 B 错误； C、32.42，故 C 正确； D、2.42，故 D 错误 故选：C 【点评】本题考查了数轴，数轴上点的位置关系是解题关键 3 （3 分）下列二次根式中，能与合并的是（ ） A B C D 【分析】先将各二次根式化为最简二次根式，然后根据同类二次根式即可判断 【解答】解： （A）原式，故 A 与不能合并； （B）原式2，故 B 与能合并； （C）原式2，故 C 与不能合并； 第 7 页（共 26 页） （D）原式2，故 D 与不能合并； 故选：B 【点评】本题考查同类二次
13、根式，解题的关键是将各根式化为最简二次根式，本题属于 基础题型 4 （3 分）如果一组数据 1，2，x，5，6 的众数为 6，则这组数据的中位数为（ ） A1 B2 C5 D6 【分析】根据众数的定义先求出 x 的值，再把数据按从小到大的顺序排列，找出最中间 的数，即可得出答案 【解答】解：数据 1，2，x，5，6 的众数为 6， x6， 把这些数从小到大排列为：1，2，5，6，6，最中间的数是 5， 则这组数据的中位数为 5； 故选：C 【点评】此题考查了确定一组数据的中位数的能力注意找中位数的时候一定要先排好 顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即 为
14、所求，如果是偶数个则找中间两位数的平均数 5 （3 分）二次函数 y（x2）2+7 的顶点坐标是（ ） A （2，7） B （2，7） C （2，7） D （2，7） 【分析】根据二次函数的顶点式解析式写出即可 【解答】解：二次函数 y（x2）2+7 为顶点式， 图象的顶点坐标是（2，7） 故选：B 【点评】本题主要考查了二次函数的性质，掌握 ya（xh）2+k 的顶点坐标为（h，k） 是解决问题的关键 6 （3 分）下列说法正确的是（ ） A面积相等的两个三角形一定全等 B平分弦的直径垂直于弦 C矩形的对角线互相平分且相等 D对角线互相垂直的四边形是菱形 【分析】根据全等三角形的判定与性质、
15、垂径定理及其推论、矩形的性质、菱形的判定 第 8 页（共 26 页） 逐一判断即可得 【解答】解：A、面积相等的两个三角形一定全等，错误； B、平分弦的直径垂直于弦，这条弦不能是直径，此结论错误； C、矩形的对角线互相平分且相等，此结论正确； D、对角线互相垂直且互相平分的四边形是菱形，此说法错误； 故选：C 【点评】本题主要考查垂径定理等知识点，解题的关键是掌握全等三角形的判定与性质、 垂径定理及其推论、矩形的性质、菱形的判定 7 （3 分）若一个等腰三角形的两边长分别为 2 和 4，则这个等腰三角形的周长是为（ ） A8 B10 C8 或 10 D6 或 12 【分析】因为等腰三角形的两边
16、分别为 2 和 4，但没有明确哪是底边，哪是腰，所以有两 种情况，需要分类讨论 【解答】解：当 2 为底时，其它两边都为 4，2、4、4 可以构成三角形，周长为 10； 当 2 为腰时，其它两边为 2 和 4，因为 2+24，所以不能构成三角形，故舍去 答案只有 10 故选：B 【点评】本题主要考查了等腰三角形的性质和三角形的三边关系；对于底和腰不等的等 腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下 分类讨论 8 （3 分）正多边形的一个内角为 135，则该多边形的边数为（ ） A5 B6 C7 D8 【分析】一个正多边形的每个内角都相等，根据内角与外角互为邻补
17、角，因而就可以求 出外角的度数，根据任何多边形的外角和都是 360 度，利用 360 除以外角的度数就可以 求出外角和中外角的个数，即多边形的边数 【解答】解：正多边形的一个内角为 135， 外角是 18013545， 360458， 则这个多边形是八边形， 故选：D 【点评】本题考查了外角和的大小与多边形的边数无关，由外角和求正多边形的边数， 第 9 页（共 26 页） 难度适中 9 （3 分） 如图， 一座石拱桥是圆弧形其跨度 AB24 米， 半径为 13 米， 则拱高 CD 为 （ ） A3米 B5 米 C7 米 D8 米 【分析】设点 O 为圆弧 AB 的圆心，利用垂径定理和勾股定理即
18、可求出答案 【解答】解：设 O 为圆心，连接 OA、OD， 由题意可知：ODAB，OA13 由垂径定理可知：ADAB12， 由勾股定理可知：OD5， CDOCCD8， 故选：D 【点评】本题考查垂径定理，涉及勾股定理，属于基础题型 10 （3 分）如果将一副三角板按如图方式叠放，那么1（ ） A90 B100 C105 D135 【分析】直接利用一副三角板的内角度数，再结合三角形外角的性质得出答案 【解答】解：如图所示：由题意可得，245， 则12+6045+60105 故选：C 第 10 页（共 26 页） 【点评】此题主要考查了三角形的外角以及三角尺的特征，正确利用三角形外角的性质 是解题
19、关键 11 （3 分）反比例函数 y的图象在第二、四象限，点 A（2，y1） 、B（4，y2） 、C（5， y3）是图象上的三点，则 y1，y2，y3的大小关系是（ ） Ay1y2y3 By1y3y2 Cy3y1y2 Dy2y3y1 【分析】根据反比例函数的性质得出点 A 在第二象限、点 B、C 在第四象限，再根据坐 标得出选项即可 【解答】解：反比例函数 y的图象在第二、四象限，点 A（2，y1） 、B（4，y2） 、 C（5，y3）是图象上的三点， 又2045， y1y3y2， 故选：B 【点评】本题考查了反比例函数的图象和性质，能熟记反比例函数的性质的内容是解此 题的关键 12 （3 分
20、）如图，正方形 ABCD 的边长为 4，点 E 是正方形外一动点，且点 E 在 CD 的右 侧，AED45，P 为 AB 的中点，当 E 运动时，线段 PE 的最大值为（ ） A4 B3 C2+2 D2+2 【分析】连接 AC，BD 交于点 O，连接 PO，EO，根据 A，C，E，D 四点共圆，可得 OE ODBD2，再根据 PEOP+OE2+2，可得当点 O 在线段 PE 上时，PE OP+OE2+2，即线段 PE 的最大值为 2+2 【解答】解：如图，连接 AC，BD 交于点 O，连接 PO，EO， 第 11 页（共 26 页） AED45，ACD45， A，C，E，D 四点共圆， 正方形
21、 ABCD 的边长为 4， OEODBD2， P 为 AB 的中点，O 是 BD 的中点， OPAD2， PEOP+OE2+2， 当点 O 在线段 PE 上时，PEOP+OE2+2， 即线段 PE 的最大值为 2+2， 故选：D 【点评】本题主要考查了正方形的性质、四点共圆、圆周角定理等知识的综合应用；熟 练掌握正方形的性质，证明四点共圆是解决问题的关键 二、填空题（本大题共二、填空题（本大题共 6 小题，每小题小题，每小题 3 分，共分，共 36 分）分） 13 （3 分）从，0，3.14，6 这五个数中随机抽取一个数，抽到的无理数的概率 是 【分析】直接利用概率公式计算得出答案 【解答】解
22、：从，0，3.14，6 这五个数中随机抽取一个数，抽到的无理数的 有，这 2 种可能， 抽到的无理数的概率是， 故答案为： 【点评】此题主要考查了概率公式，正确得出无理数的个数是解题关键 第 12 页（共 26 页） 14 （3 分）若分式的值为零，则 x 2 【分析】根据分式的值为零的条件可以求出 x 的值 【解答】解：由分式的值为零的条件得 x240，2x40， 由 x240，得 x2 或 x2， 由 2x40，得 x2， 综上，得 x2， 故答案为2 【点评】若分式的值为零，需同时具备两个条件： （1）分子为 0； （2）分母不为 0这两 个条件缺一不可 15 （3 分）如图，直线 ab
23、，P75，230，则1 45 【分析】过 P 作 PM直线 a，求出直线 abPM，根据平行线的性质得出FPM 145，即可求出答案 【解答】解：过 P 作 PM直线 a， 直线 ab， 直线 abPM， 230， EPM230， 又EPF75， FPM45， 1FPM45， 故答案为：45 【点评】本题考查了平行线的性质的应用，能正确根据平行线的性质进行推理是解此题 的关键，注意：两直线平行，内错角相等 16 （3 分）如图，四边形 ABCD 内接于O，E 是 BC 延长线上一点，若BAD100， 第 13 页（共 26 页） 则DCE 的大小是 100 【分析】直接利用圆内接四边形的性质求
24、解 【解答】解：四边形 ABCD 内接于O， DCEBAD100 故答案为 100 【点评】本题考查了圆内接四边形的性质：圆内接四边形的对角互补圆内接四边形的 任意一个外角等于它的内对角（就是和它相邻的内角的对角） 17 （3 分）若圆锥的底面积为 16cm2，母线长为 12cm，则它的侧面展开图的圆心角为 120 【分析】设圆锥的底面圆的半径为 r，利用圆的半径公式解得 r4，再利用圆锥的侧面 展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长 和弧长公式得到 24，然后解关于 n 的方程即可 【解答】解：设圆锥的底面圆的半径为 r，圆锥的侧面展开图的圆心角为 n，
25、 根据题意得 r216，解得 r4， 所以 24，解得 n120， 即圆锥的侧面展开图的圆心角为 120 故答案为 120 【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆 锥底面的周长，扇形的半径等于圆锥的母线长 18 （3 分）若关于 x 的一元二次方程 kx26x+90 有两个不相等的实数根，则 k 的取值范 围 k1 且 k0 【分析】因为关于 x 的一元二次方程 kx26x+90 有两个不相等的实数根，所以 k0 且b24ac0，建立关于 k 的不等式组，解得 k 的取值范围即可 【解答】解：关于 x 的一元二次方程 kx26x+90 有两个不相等的实数根
26、， 第 14 页（共 26 页） k0，且b24ac3636k0， 解得 k1 且 k0 故答案为 k1 且 k0 【点评】本题考查了一元二次方程根的判别式的应用切记不要忽略一元二次方程二次 项系数不为零这一隐含条件 总结：一元二次方程根的情况与判别式的关系： （1）0方程有两个不相等的实数根； （2）0方程有两个相等的实数根； （3）0方程没有实数根 三、解答题（本大题共三、解答题（本大题共 8 小题，共小题，共 66 分）分） 19 （6 分）计算：22+（2018）02sin60+|1| 【分析】直接利用零指数幂的性质以及特殊角的三角函数值和绝对值的性质化简进而得 出答案 【解答】解：原
27、式4+12+1 4+1+1 4 【点评】此题主要考查了实数运算，正确化简各数是解题关键 20 （6 分）已知 xy，求代数式（x+1）22x+y（y2x）的值 【分析】根据完全平方公式、单项式乘多项式和合并同类项可以解答本题 【解答】解： （x+1）22x+y（y2x） x2+2x+12x+y22xy x22xy+y2+1 （xy）2+1， 当 xy时，原式（）2+13+14 【点评】本题考查整式的混合运算化简求值，解答本题的关键是明确整式化简求值的 计算方法 21 （8 分）长沙市文化底蕴深厚，旅游资源丰富，天心阁、岳麓山、橘子洲三个景区是人 们节假日游玩的热点景区，李老师对九年级 1 班学
28、生五一长假随父母到这三个景区游玩 的计划做了全面调查，调查分四个类别：A、游三个景区；B、游两个景区；C、游一个 第 15 页（共 26 页） 景区；D、不到这三个景区游玩现根据调查结果绘制了不完整的条形统计图和扇形统计 图，请结合图中信息解答下列问题： （1）九（1）班共有学生 50 人，请将条形统计图补充完整； （2）在扇形统计图中，表示“B 类别”的扇形的圆心角的度数为 72 ； （3）若小明、小华两名同学，各自从三个景区中随机选一个作为 5 月 1 日游玩的景区， 请用列表或者画树状图的形式求出他们同时选中岳麓山的概率 【分析】 （1）由 A 类 5 人，占 10%，可求得总人数，求得
29、 D 类别的人数，则可将条形统 计图补充完整； （2）求得 B 类别占的百分数，则可求得“B 类别”的扇形的圆心角的度数； （3）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与他们同时选中岳 麓山的情况，再利用概率公式求解即可求得答案 【解答】解： （1）A 类 5 人，占 10%， 九（1）班共有学生有：510%50（人） ； D 类别人数为 50（5+10+15）20 人， 补全图形如下： 故答案为：50； 第 16 页（共 26 页） （2）在扇形统计图中，表示“B 类别”的扇形的圆心角的度数为：36072； 故答案为：72； （3）分别用 1，2，3 表示天心阁、岳麓山、橘
30、子洲，画树状图得： 共有 9 种等可能的结果，他们同时选中岳麓山的只有 1 种情况， 他们同时选中岳麓山的概率为 【点评】此题考查了列表法或树状图法求概率以及扇形与条形统计图的知识注意掌握 扇形统计图与条形统计图的对应关系用到的知识点为：概率所求情况数与总情况数 之比 22 （8 分）如图，某公安海上缉私局发现在我国领海的 P 处有一条走私船正以 22 海里/时 的速度沿南偏东 64的方向向公海逃窜，于是缉私局命令位于点 P 北偏东 30方向 A 处的我公安缉私快艇前往拦截，已知 P、A 相距 20 海里，公安缉私快艇向正南方向行进 计划在 B 处拦截走私船 （1）求 A、B 两处的距离； （
31、结果保留整数） （2） 若公安缉私快艇要在 B 处成功拦截走私船， 则缉私快艇的速度至少为多少海里/时？ 【参考数据： sin640.90， cos640.44， tan642，1.4，】 【分析】（1） 过 P 作 PCAB 于 C， 先解 RtACP， 求得 PCPA10 海里， ACPC 10海里再解 RtPBC，得出 BC5 海里，代入 AC+CB 即可求出 AB； （2）解 RtPBC，求出 PB11 海里，再根据公安缉私快艇行驶 AB 所需的 第 17 页（共 26 页） 时间走私船行驶 PB 所需的时间列出不等式，求解即可 【解答】解： （1）过 P 作 PCAB 于 C， 在
32、RtACP 中，A30，PA20 海里， PCPA10 海里，ACPC10海里 在 RtPBC 中，B64， BC5（海里） ， ABAC+CB10+522（海里） 答：A、B 两处的距离约为 22 海里； （2）在 RtPBC 中，PBC64， PB11（海里） 设缉私快艇的速度为 x 海里/时，由题意，得 ，即， 解得 x44 答：缉私快艇的速度至少为 44 海里/时 【点评】本题主要考查了解直角三角形的应用方向角问题，在此类题目中常用的方法 是利用作高线转化为直角三角形进行计算 23 （9 分） “低碳生活，绿色出行” ，共享单车已经成了很多人出行的主要选择，今年 1 月 份， “摩拜”
33、共享单车又向长沙河西新投放共享单车 640 辆 （1） 若 1月份到 3月份新投放单车数量的月平均增长率相同， 3月份新投放共享单车 1000 辆求月平均增长率 （2）考虑到共享单车市场竞争激烈，摩拜公司准备用不超过 60000 元的资金再购进 A， B 两种规格的自行车 100 辆，且 A 型车不超过 60 辆已知 A 型的进价为 500 元/辆，B 第 18 页（共 26 页） 型车进价为 700 元/辆，设购进 A 型车 m 辆，求出 m 的取值范围 （3） 已知 A 型车每月产生的利润是 100 元/辆， B 型车每月产生的利润是 90 元/辆， 在 （2） 的条件下，求公司每月的最大
34、利润 【分析】 （1）设月平均增长率为 x，根据“1 月份到 3 月份新投放单车数量的月平均增长 率相同，3 月份新投放共享单车 1000 辆”列出关于 x 的一元二次方程，解之即可， （2）设购进 A 型车 m 辆，则购进 B 型车（100m）辆，根据“A 型的进价为 500 元/辆， B 型车进价为 700 元/辆”列出关于 m 的一元一次不等式，结合 A 型车不超过 60 辆，列 出关于 m 的一元一次不等式组，解之即可， （3）设公司每月的利润为 W，根据“A 型车每月产生的利润是 100 元/辆，B 型车每月产 生的利润是 90 元/辆” ，列出 W 关于 m 的一次函数，结合（2）
35、中 m 的取值范围，利用一 次函数的增减性即可得到答案 【解答】解： （1）设月平均增长率为 x， 由题意得：640（1+x）21000， 解得：x12.25（舍去） ，x20.25， 答：月平均增长率为 25%， （2）设购进 A 型车 m 辆，则购进 B 型车（100m）辆， 根据题意得：500m+700（100m）60000， 解得：m50， 又A 型车不超过 60 辆， 50m60， 答：m 的取值范围为 50m60， （3）设公司每月的利润为 W， 根据题意得：W100m+90（100m）10m+9000， 50m60， 又一次函数 W 随着 m 的增大而增大， 当 m60 时，W最
36、大600+90009600（元） ， 答：公司每月的最大利润为 9600 元 【点评】本题考查一次函数的应用，一元二次方程的应用和一元一次不等式组的应用， 解题的关键： （1）根据等量关系列出一元二次方程， （2）根据不等量关系列出不等式组， （3）利用一次函数的增减性求最值 第 19 页（共 26 页） 24 （9 分）如图，已知 AO 为 RtABC 的角平分线，ACB90，以 O 为圆心， OC 为半径的圆分别交 AO，BC 于点 D，E，连接 ED 并延长交 AC 于点 F （1）求证：AB 是O 的切线； （2）求 tanCAO 的值 （3）若O 的半径为 4，求的值 【分析】 （1
37、）作 OHAB 于 H只要证明 OHOC 即可； （2）假设 AC4k，BC3k，则 AB5k，因为 AC 是O 的切线，AH 是O 的切线， 推出 AHAC4k，BHk，设 OCr，推出 OB3kr，在 RtOBH 中， （3kr）2 r2+k2，求出 r 与 k 关系即可解决问题； （3）想办法求出 AD、CF 即可解决问题； 【解答】 （1）证明：作 OHAB 于 H OA 平分CAB，OCBC，OHAB， OHOC， AB 是O 的切线 （2）解：AC：BC4：3， 可以假设 AC4k，BC3k，则 AB5k， ACO90， 第 20 页（共 26 页） OCAC， AC 是O 的切线
38、，AH 是O 的切线， AHAC4k，BHk，设 OCr， OB3kr， 在 RtOBH 中， （3kr）2r2+k2， rk， tanCAO， （3）解：连接 CD， EC 是直径， EDC90， DCF+DCO90，DCO+CED90， DCFCED， OEOD， OEDODEADF， ADFACD， DAFCAD， ADFACD， AD2AFAC， r4， k3， AC12，OA4，AD44， （44）212AF， AF（112） ， CFACAF12（112）， 【点评】本题考查相似三角形的判定和性质、解直角三角形、圆周角定理、切线的判定 第 21 页（共 26 页） 和性质等知识，解
39、题的关键是学会添加常用辅助线，学会理由参数构建方程解决问题， 属于中考压轴题 25 （10 分）定义：如图 1，点 M、N 把线段 AB 分割成 AM、MN 和 BN，若以 AM、MN、 BN 为边的三角形是一个直角三角形，则称点 M、N 是线段 AB 的勾股点 （1）已知点 M、N 是线段 AB 的勾股点，若 AM1，MN2，求 BN 的长； （2）如图 2，点 P（a，b）是反比例函数 y（x0）上的动点，直线 yx+2 与坐 标轴分别交于 A、B 两点，过点 P 分别向 x、y 轴作垂线，垂足为 C、D，且交线段 AB 于 E、F证明：E、F 是线段 AB 的勾股点； （3） 如图 3，
40、 已知一次函数 yx+3 与坐标轴交于 A、 B 两点， 与二次函数 yx24x+m 交于 C、D 两点，若 C、D 是线段 AB 的勾股点，求 m 的值 【分析】 （1）根据勾股点的定理，即可求出 BN 的长度； （2） 利用一次函数图象上点的坐标特征结合反比例函数图象上点的坐标特征， 找出点 A、 B、E、F 的坐标，利用两点间的距离公式可求出 BF、EF、AE 的长度，由 BF2+AE2EF2 即可证出 E、F 是线段 AB 的勾股点； （3）利用一次函数图象上点的坐标特征可得出点 A、B 的坐标，将一次函数解析式代入 二次函数解析式中利用解一元二次方程可得出点 C、D 的横坐标，进而可
41、得出 AC、CD、 BD 的长度，结合 C、D 是线段 AB 的勾股点，即可得出关于 m 的一元二次方程，解之取 其正值即可得出结论 【解答】解： （1）点 M、N 是线段 AB 的勾股点， BN或 BN， BN 的长为或 （2）点 P（a，b）是反比例函数 y（x0）上的动点， 第 22 页（共 26 页） b 直线 yx+2 与坐标轴分别交于 A、B 两点， 点 B 的坐标为（0，2） ，点 A 的坐标为（2，0） ； 当 xa 时，yx+22a， 点 E 的坐标为（a，2a） ； 当 y时，有x+2， 解得：x2， 点 F 的坐标为（2，） BF（2） ，EF |2a|，AE（2a） B
42、F2+AE216+2a28a+EF2， 以 BF、AE、EF 为边的三角形是一个直角三角形， E、F 是线段 AB 的勾股点 （3）一次函数 yx+3 与坐标轴交于 A、B 两点， 点 A 的坐标为（0，3） ，点 B 的坐标为（3，0） 将 yx+3 代入 yx24x+m 中，整理得：x23x+m30， 解得：xC，xD， AC（xC0），CD（xDxC），BD（3 xD） C、D 是线段 AB 的勾股点， CD2AC2+BD2，即 428m304m6， 整理得：4m2+12m1530， 解得：m1（舍去） ，m2， m 的值为 第 23 页（共 26 页） 【点评】本题考查了一次函数图象上
43、点的坐标、勾股定理、两点间的距离公式以及解无 理方程，解题的关键是： （1）利用勾股定理求出 BN 的长度； （2）利用勾股定理逆定理 证出以 BF、AE、EF 为边的三角形是一个直角三角形； （3）利用勾股定理找出关于 m 的 无理方程 26 （10 分）如图，在平面直角坐标系 xOy 中，将抛物线 yx2的对称轴绕着点 P（0，2） 顺时针旋转 45后与该抛物线交于 A，B 两点，点 Q 是该抛物线上的一点 （1）求 A，B 两点的坐标 （2）如图，若点 Q 在直线 AB 的下方，求点 Q 到直线 AB 的距离的最大值； （3）如图，若点 Q 在 y 轴左侧，且点 T（0，t） （t2）是
44、直线 PO 上一点，当以 P， B，Q 为顶点的三角形与PAT 相似时，求所有满足条件的 t 的值 【分析】 （1）根据题意易得点 M、P 的坐标，利用待定系数法来求直线 AB 的解析式，根 据解方程组，可得答案； （2）如图，过点 Q 作 x 轴的垂线 QC，交 AB 于点 C，再过点 Q 作直线 AB 的垂线， 垂足为 D，构建等腰直角QDC，利用二次函数图象上点的坐标特征和二次函数最值的 求法进行解答； （3）根据相似三角形的对应角相等推知：PBQ 中必有一个内角为 45；需要分类讨 论： PBQ45和PQB45； 然后对这两种情况下的PAT 是否是直角三角形分别 第 24 页（共 26
45、 页） 进行解答另外，以 P、B、Q 为顶点的三角形与PAT 相似也有两种情况：QPB PAT、QBPPAT 【解答】解： （1）如图， 设直线 AB 与 x 轴的交点为 M OPA45， OMOP2，即 M（2，0） 设直线 AB 的解析式为 ykx+b（k0） ，将 M（2，0） ，P（0，2）两点坐标代入，得 ， 解得 故直线 AB 的解析式为 yx+2， 联立直线 AB 与抛物线 yx2，得 ， 解得， A 点坐标是（1，1） ，B 点坐标是（2，4） ； （2）如图，过点 Q 作 x 轴的垂线 QC，交 AB 于点 C，再过点 Q 作直线 AB 的垂线， 垂足为 D， 根据条件可知Q
46、DC 为等腰直角三角形，则 QDQC 设 Q（m，m2） ，则 C（m，m+2） QCm+2m2（m）2+， QDQC（m）2+ 第 25 页（共 26 页） 故当 m时，点 Q 到直线 AB 的距离最大，最大值为； （3）APT45， PBQ 中必有一个内角为 45，由图知，BPQ45不合题意 如图， 若PBQ45，过点 B 作 x 轴的平行线，与抛物线和 y 轴分别交于点 Q、F此时满 足PBQ45 Q（2，4） ，F（0，4） ， 此时BPQ是等腰直角三角形，由题意知PAT 也是等腰直角三角形 （i）当PTA90时，得到：PTAT1，此时 t1； （ii）当PAT90时，得到：PT2，此时
