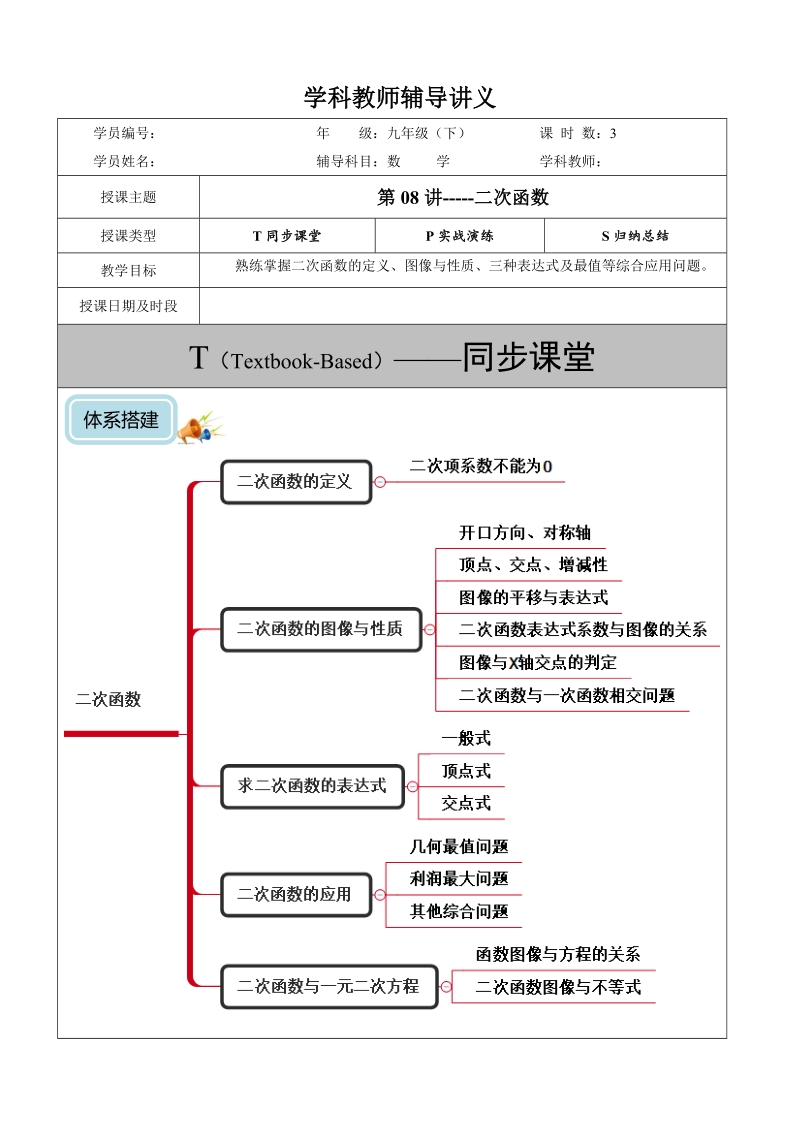
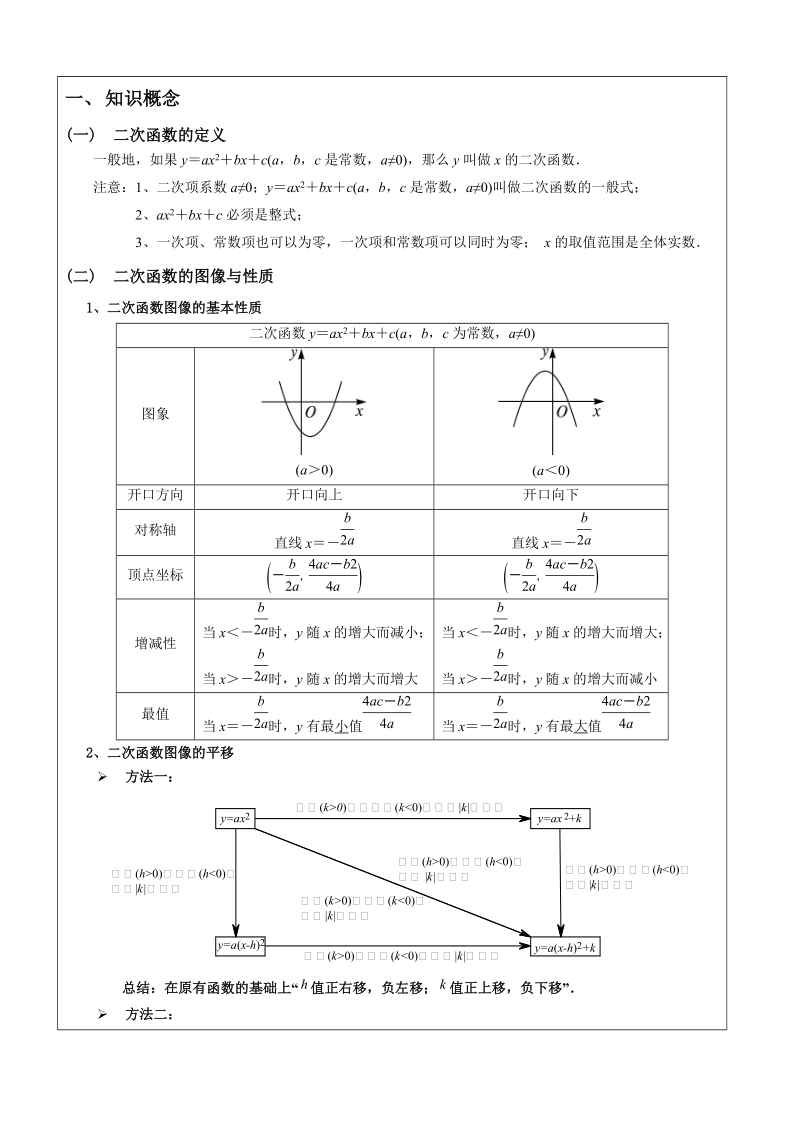
1、学科教师辅导讲义学员编号： 年 级：九年级（下）课 时 数：3学员姓名：辅导科目：数 学学科教师：授课主题第08讲-二次函数授课类型T同步课堂P实战演练S归纳总结教学目标熟练掌握二次函数的定义、图像与性质、三种表达式及最值等综合应用问题。授课日期及时段T（Textbook-Based）同步课堂体系搭建一、 知识概念(一) 二次函数的定义一般地，如果yax2bxc(a，b，c是常数，a0)，那么y叫做x的二次函数注意：1、二次项系数a0；yax2bxc(a，b，c是常数，a0)叫做二次函数的一般式；2、ax2bxc必须是整式；3、一次项、常数项也可以为零，一次项和常数项可以同时为零； x的取值范
2、围是全体实数(二) 二次函数的图像与性质1、二次函数图像的基本性质二次函数yax2bxc(a，b，c为常数，a0)图象(a0)(a0)开口方向开口向上开口向下对称轴直线x直线x顶点坐标增减性当x时，y随x的增大而减小；当x时，y随x的增大而增大当x时，y随x的增大而增大；当x时，y随x的增大而减小最值当x时，y有最小值当x时，y有最大值2、二次函数图像的平移 方法一： 总结：在原有函数的基础上“值正右移，负左移；值正上移，负下移” 方法二：沿轴平移:向上（下）平移个单位，变成（或）沿轴平移：向左（右）平移个单位，变成（或）总结：概括成八个字“左加右减，上加下减” 3、二次函数的图象与各项系数之
3、间的关系 （1） 二次项系数的正负决定开口方向，的大小决定开口的大小（2）一次项系数：在确定的前提下，决定了抛物线对称轴的位置， “左同右异”。 （3） 常数项：决定了抛物线与轴交点的位置 总之，只要都确定，那么这条抛物线就是唯一确定的(三) 二次函数的表达式1、一般式：（，为常数，）；2、顶点式：（，为常数，）；3、两根式：（，是抛物线与轴两交点的横坐标）.使用条件：1、已知抛物线上三点的坐标，一般选用一般式；2、已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3、已知抛物线与轴的两个交点的横坐标，一般选用两根式；4、已知抛物线上纵坐标相同的两点，常选用顶点式(四) 二次函数的应用解题
4、一般方法步骤（先构造二次函数模型）：（1）列出二次函数的解析式，列解析式时，要根据自变量的实际意义，确定自变量的取值范围（2）在自变量取值范围内，运用公式法或配方法或对称轴判定法，求出二次函数的最大值或最小值(五) 二次函数与一元二次方程（1）二次函数yax2bxc(a0)，当y0时，就变成了ax2bxc0(a0)（2）ax2bxc0(a0)的解是抛物线与x轴交点的横坐标（3）当0时，有两个不同的交点；当0时，有一个交点；当c0时，抛物线与x轴没有交点考点一： 二次函数的定义例1、若y=（1+m）是二次函数，且开口向下，则m的值为（）A3 B3 C+3 D0例2、下列函数关系中，可以看做二次函
5、数y=ax2+bx+c模型的是（）A在一定距离内，汽车行驶的速度与行驶的时间的关系B我国人中自然增长率为1%，这样我国总人口数随年份变化的关系C竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）D圆的周长与半径之间的关系考点二： 二次函数的图像与性质例1、一次函数y=ax+b（a0）与二次函数y=ax2+bx+c（a0）在同一平面直角坐标系中的图象可能是（）A B C D例2、如图，已知二次函数y=ax2+bx+c（a0）的图象与x轴交于点A（1，0），与y轴的交点B在（0，2）和（0，1）之间（不包括这两点），对称轴为直线x=1下列结论：abc0； 4a+2b+
6、c0 ；4acb28a ；a；bc其中含所有正确结论的选项是（）A B C D例3、若抛物线y=x22x+3不动，将平面直角坐标系xOy先沿水平方向向右平移一个单位，再沿铅直方向向上平移三个单位，则原抛物线图象的解析式应变为（）Ay=（x2）2+3 By=（x2）2+5 Cy=x21 Dy=x2+4考点三： 二次函数的表达式例1、把二次函数y=x2x+3配方化为y=a（xh）2+k形式（）Ay=（x2）2+2 By=（x2）2+4 Cy=（x+2）2+4 Dy=（x1）2+3例2、二次函数图象如图所示，则其解析式是（）Ay=x2+2x+4 By=x2+2x+4Cy=x22x+4 Dy=x2+2
7、x+3考点四： 二次函数的应用例1、将抛物线y=x2+2x+3在x轴上方的部分沿x轴翻折至x轴下方，图象的剩余部分不变，得到一个新的函数图象，那么直线y=x+b与此新图象的交点个数的情况有（）种A6 B5 C4 D3例2、某校校园内有一个大正方形花坛，如图甲所示，它由四个边长为3米的小正方形组成，且每个小正方形的种植方案相同其中的一个小正方形ABCD如图乙所示，DG=1米，AE=AF=x米，在五边形EFBCG区域上种植花卉，则大正方形花坛种植花卉的面积y与x的函数图象大致是（）A B C D例3、某玩具厂生产一种玩具，本着控制固定成本，降价促销的原则，使生产的玩具能够全部售出据市场调查，若按每
8、个玩具280元销售时，每月可销售300个若销售单价每降低1元，每月可多售出2个据统计，每个玩具的固定成本Q（元）与月产销量y（个）满足如下关系：月产销量y（个）160200240300每个玩具的固定成本Q（元）60484032（1）写出月产销量y（个）与销售单价x （元）之间的函数关系式；（2）求每个玩具的固定成本Q（元）与月产销量y（个）之间的函数关系式；（3）若每个玩具的固定成本为30元，则它占销售单价的几分之几？（4）若该厂这种玩具的月产销量不超过400个，则每个玩具的固定成本至少为多少元？销售单价最低为多少元？考点五：二次函数与一元二次方程例1、已知抛物线y=ax22x+1与x轴没有交
9、点，那么该抛物线的顶点所在的象限是（）A第四象限 B第三象限 C第二象限 D第一象限例2、如图，一段抛物线y=x（x3）（0x3），记为C1，它与x轴交于点O和A1；将C1绕A1旋转180得到C2，交x轴于A2；将C2绕A2旋转180得到C3，交x轴于A3，如此进行下去，得到一条“波浪线”若点P（41，m）在此“波浪线”上，则m的值为（）A2 B2 C0 DP(Practice-Oriented)实战演练实战演练 课堂狙击1、若y=（a2+a）是二次函数，那么（）Aa=1或a=3 Ba1或a0 Ca=3 Da=12、下列函数关系中，是二次函数的是（）A在弹性限度内，弹簧的长度y与所挂物体的质量
10、x之间的关系B当距离一定时，汽车行驶的时间t与速度v之间的关系C矩形的面积S和矩形的宽x之间的关系D等边三角形的面积S与边长x之间的关系3、二次函数y=ax2+bx+c（a0）图象上部分点的坐标（x，y）对应值列表如下：x32101y323611则该函数图象的对称轴是（）A直线x=3 B直线x=2 C直线x=1 D直线x=04、如图是抛物线y=ax2+bx+c（a0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间则下列结论：ab+c0；3a+b=0；b2=4a（cn）；一元二次方程ax2+bx+c=n1有两个不相等的实数根其中正确结论的个数是（）A1 B2
11、 C3 D45、将抛物线y=x24x4向左平移3个单位，再向上平移5个单位，得到抛物线的表达式为（）Ay=（x+1）213 By=（x5）23 Cy=（x5）213 Dy=（x+1）236、二次函数y=ax2+bx与一次函数y=ax+b（a0）在同一平面直角坐标系中可能的图象为（）A B C D7、如图，已知抛物线y=ax2+bx+c与轴交于A、B两点，顶点C的纵坐标为2，现将抛物线向右平移2个单位，得到抛物线y=a1x2+b1x+c1，则下列结论：b0；ab+c0；阴影部分的面积为4；若c=1，则b2=4a正确的是（）A B C D8、若二次函数y=x2+2x+m2+1的最大值为4，则实数m
12、的值为（）A B C2 D19、如图，抛物线y=x23x+与x轴相交于A、B两点，与y轴相交于点C，点D是直线BC下方抛物线上一动点，过点D作y轴的平行线，与直线BC相交于点E（1）求直线BC的解析式；（2）当线段DE的长度最大时，求点D的坐标 课后反击1、若y=（1+m）是二次函数，且开口向下，则m的值为（）A3 B3 C+3 D02、在同一平面直角坐标系内，一次函数y=ax+b与二次函数y=ax2+5x+b的图象可能是（）A BCD3、如图，抛物线y=ax2+bx+c（a0）的对称轴为直线x=1，与x轴的一个交点坐标为（1，0），其部分图象如图所示，下列结论：4acb2；方ax2+bx+c
13、=0的两个根是x1=1，x2=3；3a+c0；当y0时，x的取值范围是1x3；当x0时，y随x增大而增大其中结论正确的个数是（）A4个 B3个 C2个 D1个4、已知二次函数y=ax2+4x+a1的最小值为2，则a的值为（）A3 B1 C4 D4或15、工艺商场按标价销售某种工艺品时，每件可获利45元；按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等（1）该工艺品每件的进价、标价分别是多少元？（2）若每件工艺品按（1）中求得的进价进货，标价售出，工艺商场每天可售出该工艺品100件若每件工艺品降价1元，则每天可多售出该工艺品4件问每件工艺品降价多少元出售，每天获得的
14、利润最大？获得的最大利润是多少元？6、如图，已知ABC的三个顶点坐标分别为A（4，0）、B（1，0）、C（2，6）（1）求经过A、B、C三点的抛物线解析式；（2）设直线BC交y轴于点E，连接AE，求证：AE=CE；（3）设抛物线与y轴交于点D，连接AD交BC于点F，试问以A、B、F为顶点的三角形与ABC相似吗？（4）若点P为直线AE上一动点，当CP+DP取最小值时，求P点的坐标直击中考1、【2016广州】对于二次函数y=+x4，下列说法正确的是（）A当x0时，y随x的增大而增大 B当x=2时，y有最大值3C图象的顶点坐标为（2，7） D图象与x轴有两个交点2、【2016赤峰】函数y=k（xk）
15、与y=kx2，y=（k0），在同一坐标系上的图象正确的是（）A B C D3、【2016临沂】二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：x543210y402204下列说法正确的是（）A抛物线的开口向下 B当x3时，y随x的增大而增大C二次函数的最小值是2 D抛物线的对称轴是x=4、【2016兰州】二次函数y=ax2+bx+c的图象如图所示，对称轴是直线x=1，有以下结论：abc0；4acb2；2a+b=0；ab+c2其中正确的 结论的个数是（）A1 B2 C3 D45、【2015深圳】如图1，关于x的二次函数y=x2+bx+c经过点A（3，0），点C（0，3），点D为二次函
16、数的顶点，DE为二次函数的对称轴，E在x轴上（1）求抛物线的解析式；（2）DE上是否存在点P到AD的距离与到x轴的距离相等？若存在求出点P，若不存在请说明理由；（3）如图2，DE的左侧抛物线上是否存在点F，使2SFBC=3SEBC？若存在求出点F的坐标，若不存在请说明理由6、【2014深圳】如图，直线AB的解析式为y=2x+4，交x轴于点A，交y轴于点B，以A为顶点的抛物线交直线AB于点D，交y轴负半轴于点C（0，4）（1）求抛物线的解析式；（2）将抛物线顶点沿着直线AB平移，此时顶点记为E，与y轴的交点记为F，求当BEF与BAO相似时，E点坐标；记平移后抛物线与AB另一个交点为G，则SEFG与SACD是否存在8倍的关系？若有请直接写出F点的坐标S(Summary-Embedded)归纳总结重点回顾二次函数的定义；二次函数的图像与性质；二次函数的表达式与应用；二次函数与一元二次方程。名师点拨本章内容丰富且综合性较强，也是中考的必考点与重难点，结合教案做好总结及勤学多练是掌握的关键。学霸经验 本节课我学到 我需要努力的地方是13
