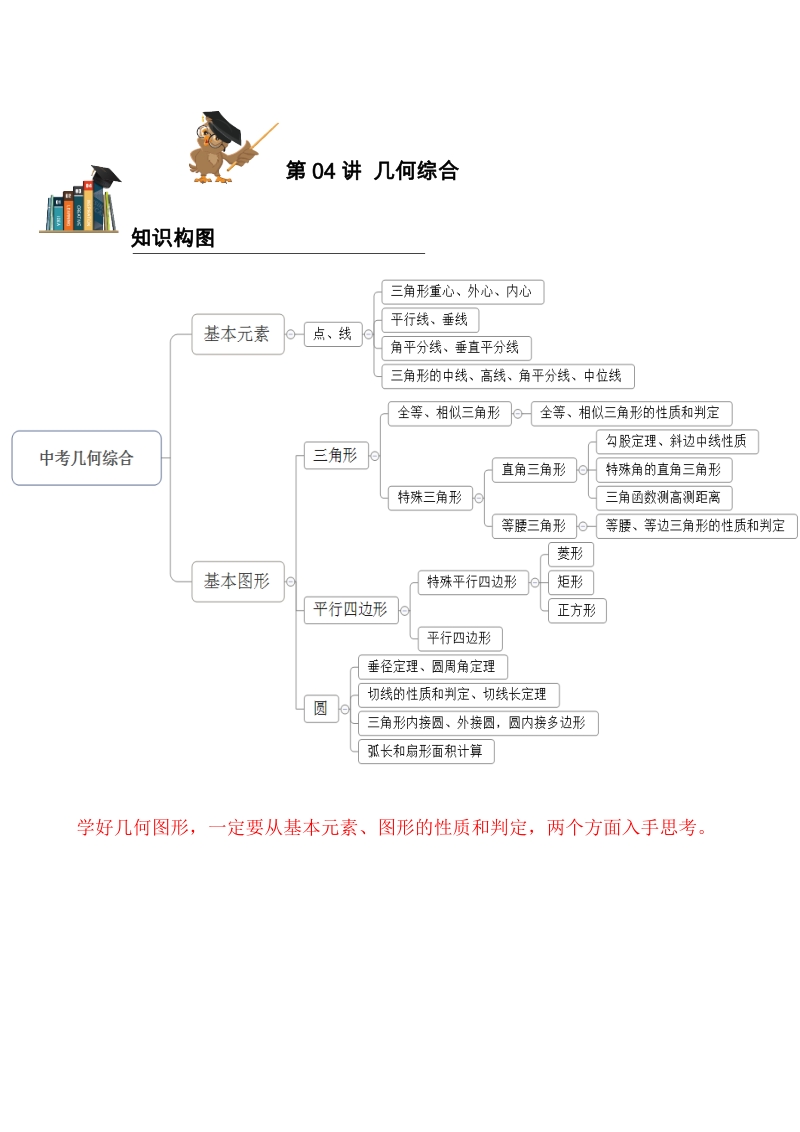
1、高效提分 源于优学 第04讲 几何综合 知识构图学好几何图形，一定要从基本元素、图形的性质和判定，两个方面入手思考。知识要点一 全等、相似三角形（一）相似三角形1、相似三角形的性质：相似三角形对应角相等，对应边成比例. 相似三角形对应高的比，对应中线的比和对应角平分线的比都等于相似比. 相似三角形周长的比等于相似比. 相似三角形面积的比等于相似比的平方.2、相似三角形的判定如果一个三角形的两个角分别与另一个三角形的两个角对应相等，那么这两个三角形相似 如果一个三角的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似 如果一个三角形的三条边分别与另一个三角形的三条边对应成
2、比例，那么这两个三角形相似（二）全等三角形1、全等三角形的性质：全等三角形的对应边相等，对应角相等。全等三角形的对应边上的中线相等，对应边上的高相等，对应角平分线相等；全等三角形的周长相等、面积相等。 2、全等三角形的判定三条边分别相等的两个三角形全等，简写成“边边边”或“SSS”. 两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA” 两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“边边角”或“AAS”两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“边边角”或“AAS”直角三角形全等条件：斜边和一条直角边分别相等的两个直角三角形全等，简写成“斜边、直
3、角边”或“HL”（三）特殊三角形1、直角三角形：（1）勾股定理：直角三角形两直角边长的平方之和等于斜边长的平方。（2）直角三角形斜边中线性质：直角三角形斜边上的中线等于斜边的一半。（四）等腰三角形1、等腰三角形的性质（1）等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合（也称三线合一）。（2）等腰三角形的两腰相等、两底角相等。 典例分析例1如图，ABC和DEF中，AB=DE、B=DEF，添加下列哪一个条件无法证明ABCDEF（）AACDF BA=D CAC=DF DACB=F【解析】C例2如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB
4、于G，连接DG，现在有如下4个结论：ADGFDG；GB=2AG；GDEBEF；SBEF=在以上4个结论中，正确的有（）A1 B2 C3 D4【解析】 C 例3如图，已知ABC，AB=AC，A=90，直角EPF的顶点P是BC的中点，两边PE，PF分别交AB，AC于点E、F给出以下四个结论：AE=CF EF=APEPF是等腰直角三角形 S四边形AEPF=SABC上述结论始终正确的有（）ABCD【解析】C ，提示如图例4如图所示、AOB和COD均为等腰直角三角形，AOB=COD=90，D在AB上（1）求证：AOCBOD（2）若AD=1，BD=2，求CD的长【解析】（1）证明：DOB=90AOD，AO
5、C=90AODBOD=AOC又OC=OD，OA=OB在AOC和BOD中，AOCBOD（SAS）（2）解：AOCBODAC=BD=2，CAO=DBO=45CAB=CAO+BAO=90CD=例5如图，直角梯形ABCD中，DAB=90，ABCD，AB=AD，ABC=60以AD为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且EAD=EDA=15，连接EB、EF（1）求证：EB=EF；（2）若EF=6，求梯形ABCD的面积【解析】（1）证明：ADF为等边三角形， AF=AD，FAD=60， DAB=90，EAD=15， FAE=FAD+EAD=75，BAE=DABEAD=75
6、， FAE=BAE， 又AD=AB， AB=AF， 在FAE和BAE中， FAEBAE（SAS）， EF=EB；（2）在FAE和FDE中，FAEFDE（SSS），DFE=AFE=60=30，DEF=AEF=150=75，又FAE=60+15=75，AEF=FAE，又EF=6，AF=EF=6，AB=AD=AF=6，过C作CMAB于M，可得CM=AD=6，tanABC=，ABC=60，BM=2，CD=AM=ABBM=6，S梯形ABCD=（62）+66=366学霸说三角形中的线段长度求值方法：（1）中考热门考点是利用相似三角形的相似比来求线段长度（2）除了利用相似，还可以利用勾股定理、等腰三角形性质
7、、三角形中位线、直角三角形斜边中线性质等。的残酷的掠夺，激起。举一反三1如图，在ABC中，ACB=90，AC=BC=1，E、F为线段AB上两动点，且ECF=45，过点E、F分别作BC、AC的垂线相交于点M，垂足分别为H、G有以下结论：AB=；当点E与点B重合时，MH=；AF+BE=EF；MGMH=，其中正确结论的个数是（）A1B2C3D4【解析】C2如图，ABC中，AB=AC，延长BC至D，使CD=BC，点E在边AC上，以CE，CD为邻边做平行四边形CDFE，过点C作CGAB交EF于点G，连接BG，DE（1）ACB与GCD有怎样的数量关系？请说明理由；（2）求证：BCGDCE【解析】（1）解：
8、ACB=GCD 理由如下：AB=ACABC=ACBCGABABC=GCDACB=GCD （2）证明：四边形CDFE是平行四边形EFCDACB=GEC，EGC=GCDACB=GCDGEC=EGC ，EC=GCGCD=ACBGCB=ECD在BCG和DCE中，BCGDCE3如图，在四边形ABCD中，ABC=90，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN（1）求证：BM=MN；（2）BAD=60，AC平分BAD，AC=2，求BN的长【解析】（1）证明：在CAD中，M、N分别是AC、CD的中点，MNAD，MN=AD，在RTABC中，M是AC中点，BM=AC， AC=AD MN=BM
9、（2）解：BAD=60，AC平分BAD， BAC=DAC=30， 由（1）可知，BM=AC=AM=MC，BMC=BAM+ABM=2BAM=60，MNAD，NMC=DAC=30，BMN=BMC+NMC=90，BN2=BM2+MN2， 由（1）可知MN=BM=AC=1，BN=知识要点二平行四边形（一）平行四边形1、平行四边形的性质：对边分别平行且相等 对角线相互平分 对角相等2、平行四边形的判定：两组对边分别相等的四边形 一组对边平行且相等的四边形对角线相互平分的四边形（二）特殊的平行四边形1、菱形：有一组邻边相等的平行四边形（1）菱形的性质：菱形的四条边相等 菱形的对角线互相垂直（2）菱形的判定
10、：有一组邻边相等的平行四边形 对角线互相垂直的平行四边形四边相等的四边形2、矩形：有一个角为直角的平行四边形（1）矩形的性质：矩形的四个角都为直角 矩形的对角线相等（2）矩形的判定：有一个角为直角的平行四边形 对角线相等的平行四边形。有三个角为直角的四边形3、正方形：有一组邻边相等，并且有一个角是直角的平行四边形。（1）正方形的性质：正方形四个角都是直角、四条边相等 正方形的对角线相等且互相垂直平分（2）正方形的判定：有一组邻边相等的矩形 对角线垂直的矩形 有一个角是直角的菱形 对角线相等的菱形典例分析例1如图，CB=CA，ACB=90，点D在边BC上（与B、C不重合），四边形ADEF为正方形
11、，过点F作FGCA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：AC=FG；SFAB：S四边形CBFG=1：2；ABC=ABF；AD2=FQAC，其中正确的结论的个数是（）A1 B2 C3 D4【解析】D例2如图，在平行四边形ABCD中，对角线AC、BD相交于点O，E、F是对角线AC上的两点，给出下列四个条件：AE=CF；DE=BF；ADE=CBF；ABE=CDF其中不能判定四边形DEBF是平行四边形的有（）A0个 B1个 C2个 D3个【解析】B例3已知BD垂直平分AC，BCD=ADF，AFAC，（1）证明四边形ABDF是平行四边形；（2）若AF=DF=5，AD=6，求AC的
12、长【解析】（1）证明：BD垂直平分AC，AB=BC，AD=DC在ADB与CDB中，ADBCDB（SSS）BCD=BADBCD=ADFBAD=ADFABFDBDAC，AFACAFBD四边形ABDF是平行四边形（2）解：四边形ABDF是平行四边形，AF=DF=5，ABDF是菱形，AB=BD=5，AD=6，设BE=x，则DE=5x，AB2BE2=AD2DE2，即52x2=62（5x）2，解得：x=，=，AC=2AE=例4在等腰梯形ABCD中，已知ADBC，AB=DC，AC与BD交于点O，延长BC到E，使CE=AD，连接DE（1）求证：BD=DE（2）若ACBD，AD=3，SABCD=16，求AB的长
13、【解析】（1）证明：ADBC，CE=AD，四边形ACED是平行四边形，AC=DE，四边形ABCD是等腰梯形，ADBC，AB=DC，AC=BD，BD=DE（2）解：过点D作DFBC于点F，四边形ACED是平行四边形，CE=AD=3，ACDE，ACBD，BDDE，BD=DE，SBDE=BDDE=BD2=BEDF=（BC+CE）DF=（BC+AD）DF=S梯形ABCD=16，BD=4，BE=BD=8，DF=BF=EF=BE=4，CF=EFCE=1，由勾股定理得AB=CD=例5RtABC中，BAC=90，D是BC的中点，E是AD的中点，过点A作AFBC交BE的延长线于点F（1）求证：AEFDEB；（2
14、）证明四边形ADCF是菱形；（3）若AC=4，AB=5，求菱形ADCF的面积【解析】（1）证明：AFBC，AFE=DBEE是AD的中点，AD是BC边上的中线AE=DE，BD=CD在AFE和DBE中，AFEDBE（AAS）（2）证明：由（1）知，AFEDBE，则AF=DBDB=DC，AF=CDAFBC四边形ADCF是平行四边形BAC=90，D是BC的中点，E是AD的中点AD=DC=BC，四边形ADCF是菱形（3）连接DFAFBD，AF=BD四边形ABDF是平行四边形DF=AB=5四边形ADCF是菱形S菱形ADCF=ACDF=45=10举一反三1如图，矩形ABCD中，O为AC中点，过点O的直线分别
15、与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO若COB=60，FO=FC，则下列结论：FBOC，OM=CM； EOBCMB；四边形EBFD是菱形；MB：OE=3：2其中正确结论的个数是（）A1 B2 C3 D4 【解析】C2如图，在RtABC中，ACB=90，D、E分别为AB，AC边上的中点，连接DE，将ADE绕点E旋转180得到CFE，连接AF，AC（1）求证：四边形ADCF是菱形；（2）若BC=8，AC=6，求四边形ABCF的周长【解析】（1）证明：将ADE绕点E旋转180得到CFE，AE=CE，DE=EF，四边形ADCF是平行四边形，D、E分别为AB，AC边上的中点，DE
16、是ABC的中位线，DEBC，ACB=90，AED=90，DFAC，四边形ADCF是菱形；（2）解：在RtABC中，BC=8，AC=6，AB=10，D是AB边上的中点，AD=5，四边形ADCF是菱形，AF=FC=AD=5，四边形ABCF的周长为8+10+5+5=283如图，已知四边形ABCD和四边形DEFG为正方形，点E在线段DC上，点A，D，G在同一直线上，且AD=3，DE=1，连接AC，CG，AE，并延长AE交CG于点H（1）求sinEAC的值（2）求线段AH的长【解析】（1）作EMAC于M四边形ABCD是正方形ADC=90，AD=DC=3，DCA=45在RTADE中，ADE=90，AD=3
17、，DE=1AE=，在RTEMC中，EMC=90，ECM=45，EC=2，EM=CM=，在RTAEM中，sinEAM=（2）在GDC和EDA中，GDCEDA，GCD=EAD，GC=AE=，DAE+AED=90，DEA=CEH，DCG+HEC=90，EHC=90，AHGC，SAGC=AGDC=GCAH，43=AH，AH=知识要点三圆（一）圆心角、弧、弦之间的关系 在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等。（二）垂径定理1、垂径定理：垂直于弦的直径平分这条弦，并且平分这条弦所对的弧。2、推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的
18、弧。（三）圆周角定理1、圆周角定理：圆周角的度数等于它所对弧上的圆心角度数的一半。2、推论：同弧或等弧所对的圆周角相等。直径所对的圆周角是90，90的圆周角所对的弦是直径。3、圆内接四边形的对角互补（四）切线的性质及判定1、性质：圆的切线垂直于过切点的半径推论：经过圆心且垂直于切线的直线必过圆心；经过切点且垂直于切线的直线必过圆心。2、判定：过半径外端且垂直于半径的直线是圆的切线 到圆心的距离等于半径的直线是圆的切线。3、三角形的内切圆：和三角形三边都相切的圆叫做三角形的内切圆。内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心。（五）弧长及扇形的面积1、弧长公式：（R表示半径，n表示弧
19、长的圆心角）2、扇形面积公式：（R表示半径，n表示扇形的圆心角，表示扇形的弧长）典例分析1如图，AB为O直径，已知DCB=20，则DBA为（）A50 B20 C60 D70【解析】D2如图，在扇形AOB中AOB=90，正方形CDEF的顶点C是的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2时，则阴影部分的面积为（）A24 B48 C28 D44【解析】A3如图，边长为1的菱形ABCD绕点A旋转，当B、C两点恰好落在扇形AEF的弧EF上时，弧BC的长度等于（）A B C D【解析】C4如图1，已知在O中，点C为劣弧AB上的中点，连接AC并延长至D，使CD=CA，连接DB并延
20、长DB交O于点E，连接AE（1）求证：AE是O的直径；（2）如图2，连接EC，O半径为5，AC长为4，求阴影部分的面积之和 【解析】（1）证明：连接CB，AB，CE，点C为劣弧AB上的中点，CB=CA，又CD=CA，AC=CD=BC，ABC=BAC，DBC=D，Rt斜边上的中线等于斜边的一半，ABD=90，ABE=90，即弧AE的度数是180，AE是O的直径；（2）解：AE是O的直径，ACE=90，AE=10，AC=4，根据勾股定理得：CE=2，S阴影=S半圆SACE=12.542=12.54举一反三1如图，AB是O的直径，弦CD垂直平分OB，垂足为点E，连接OD、BC，若BC=1，则扇形OB
21、D的面积为 【解析】2如图，点A、B、C是圆O上的三点，且四边形ABCO是平行四边形，OFOC交圆O于点F，则BAF等于（）A12.5 B15 C20 D22.5【解析】B3如图，在ABC中，以AB为直径的O分别与BC，AC相交于点D，E，BD=CD，过点D作O的切线交边AC于点F（1）求证：DFAC；（2）若O的半径为5，CDF=30，求的长（结果保留）【解析】（1）证明：连接OD，如图所示DF是O的切线，D为切点ODDFODF=90BD=CD，OA=OBOD是ABC的中位线ODAC，CFD=ODF=90，DFAC（2）解：CDF=30由（1）得ODF=90ODB=180CDFODF=60O
22、B=ODOBD是等边三角形BOD=60的长= 课堂闯关初出茅庐1如图，ABC内接于O，AHBC于点H，若AC=24，AH=18，O的半径OC=13，则AB= 【解析】，提示如图2如图，在ABC中，AC的垂直平分线分别交AC、BC于E，D两点，EC=4，ABC的周长为23，则ABD的周长为（）A13 B15 C17 D19【解析】B3如图，F是正方形ABCD的边CD上的一个动点，BF的垂直平分线交对角线AC于点E，连接BE，FE，则EBF的度数是（）A45 B50 C60 D不确定【解析】A提示：过E作HIBC，分别交AB、CD于点H、I，证明RtBHERtEIF，可得IEF+HEB=90，再根
23、据BE=EF即可解题4如图，平行四边形ABCD中，BDAD，A=45，E、F分别是AB、CD上的点，且BE=DF，连接EF交BD于O（1）求证：BO=DO；（2）若EFAB，延长EF交AD的延长线于G，当FG=1时，求AE的长【解析】（1）证明：四边形ABCD是平行四边形DCABOBE=ODF 在OBE与ODF中OBEODF（AAS）BO=DO （2）解：EFAB，ABDCGEA=GFD=90A=45G=A=45 AE=GE BDAD，ADB=GDO=90GOD=G=45 DG=DO，OF=FG=1，由（1）可知，OE=OF=1，GE=OE+OF+FG=3，AE=3优学学霸1在矩形ABCD中，
24、AD=2AB=4，E是AD的中点，一块足够大的三角板的直角顶点与点E重合，将三角板绕点E旋转，三角板的两直角边分别交AB，BC（或它们的延长线）于点M，N，设AEM=（090），给出下列四个结论：AM=CN；AME=BNE；BNAM=2；SEMN=上述结论中正确的个数是（）A1B2C3D4 【解析】C2如图1，一张矩形纸片ABCD，其中AD=8cm，AB=6cm，先沿对角线BD对折，点C落在点C的位置，BC交AD于点G（1）求证：AG=CG；（2）如图2，再折叠一次，使点D与点A重合，得折痕EN，EN交AD于点M，求EM的长【解析】（1）证明：沿对角线BD对折，点C落在点C的位置，A=C，AB
25、=CD在GAB与GCD中GABGCDAG=CG；（2）解：点D与点A重合，得折痕EN，DM=4cm，AD=8cm，AB=6cm，在RtABD中，BD=10cm，ENAD，ABAD，ENAB，MN是ABD的中位线，DN=BD=5cm，在RtMND中，MN=3（cm），由折叠的性质可知NDE=NDC，ENCD，END=NDC，END=NDE，EN=ED，设EM=x，则ED=EN=x+3，由勾股定理得ED2=EM2+DM2，即（x+3）2=x2+42，解得x=，即EM=cm 考场直播1【2016 深圳中考】如图，已知O的半径为2，AB为直径，CD为弦AB与CD交于点M，将沿CD翻折后，点A与圆心O重
26、合，延长OA至P，使AP=OA，连接PC（1）求CD的长；（2）求证：PC是O的切线；（3）点G为的中点，在PC延长线上有一动点Q，连接QG交AB于点E交于点F（F与B、C不重合）问GEGF是否为定值？如果是，求出该定值；如果不是，请说明理由【解析】（1）解：如图，连接OC，沿CD翻折后，点A与圆心O重合，OM=OA=2=1，CDOA，OC=2，CD=2CM=2=2=2；（2）证明：PA=OA=2，AM=OM=1，CM=CD=，CMP=OMC=90，PC=2，OC=2，PO=2+2=4，PC2+OC2=（2）2+22=16=PO2，PCO=90，PC是O的切线；（3）解：GEGF是定值，证明如
27、下，连接GO并延长，交O于点H，连接HF点G为的中点，GOE=90，HFG=90，且OGE=FGHOGEFGH=，GEGF=OGGH=24=8 自我挑战1如图，ABCD，BP和CP分别平分ABC和DCB，AD过点P，且与AB垂直若AD=8，则点P到BC的距离是（）A8B6C4D2【解析】C2如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AEEF，AE=EF，现有如下结论：BE=GE；AGEECF；FCD=45；GBEECH其中，正确的结论有（）A1个B2个C3个D4个【解析】B3如图所示，ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交CE的延长线于F，且
28、AF=BD，连接BF（1）求证：D是BC的中点；（2）若AB=AC，试判断四边形AFBD的形状，并证明你的结论【解析】（1）证明：AFBC，AFE=DCE，点E为AD的中点，AE=DE，在AEF和DEC中，AEFDEC（AAS），AF=CD，AF=BD，CD=BD，D是BC的中点；（2）解：若AB=AC，则四边形AFBD是矩形理由如下：AEFDEC，AF=CD，AF=BD，CD=BD；AFBD，AF=BD，四边形AFBD是平行四边形，AB=AC，BD=CD，ADB=90，平行四边形AFBD是矩形4如图，AB是O的直径，点C、D在O上，A=2BCD，点E在AB的延长线上，AED=ABC（1）求证
29、：DE与O相切；（2）若BF=2，DF=，求O的半径【解析】（1）证明：连接OD，AB是O的直径，ACB=90，A+ABC=90，BOD=2BCD，A=2BCD，BOD=A，AED=ABC，BOD+AED=90，ODE=90，即ODDE，DE与O相切；（2）连接BD，过D作DHBF于H，DE与O相切，BDE=BCD，AED=ABC，AFC=DBF，AFC=DFB，FDB是等腰三角形，FH=BH=BF=1，则FH=1，HD=3，在RtODH中，OH2+DH2=OD2，即（OD1）2+32=OD2，OD=5，O的半径是55在RtABC中，ABC=90，以CB为半径作C，交AC于点D，交AC的延长线
30、于点E，连接ED，BE（1）求证：ABDAEB；（2）当=时，求tanE；（3）在（2）的条件下，作BAC的平分线，与BE交于点F，若AF=2，求C的半径解：（1）ABC=90，ABD=90DBC由题意知：DE是直径，DBE=90E=90BDEBC=CD，DBC=BDEABD=EA=A，ABDAEB（2）AB：BC=4：3设AB=4，BC=3，AC=5BC=CD=3，AD=ACCD=53=2由（1）可知：ABDAEB=，AB2=ADAE42=2AE，AE=8在RtDBE中tanE=（3）过点F作FMAE于点MAB：BC=4：3，设AB=4x，BC=3x由（2）可知；AE=8x，AD=2xDE=AEAD=6xAF平分BAC，=tanE=，cosE=，sinE=，BE=EF=BE=，sinE=MF=，tanE=ME=2MF=AM=AEME=AF2=AM2+MF24=+，x=C的半径为：3x= 21 2017年春季中考复习课程
