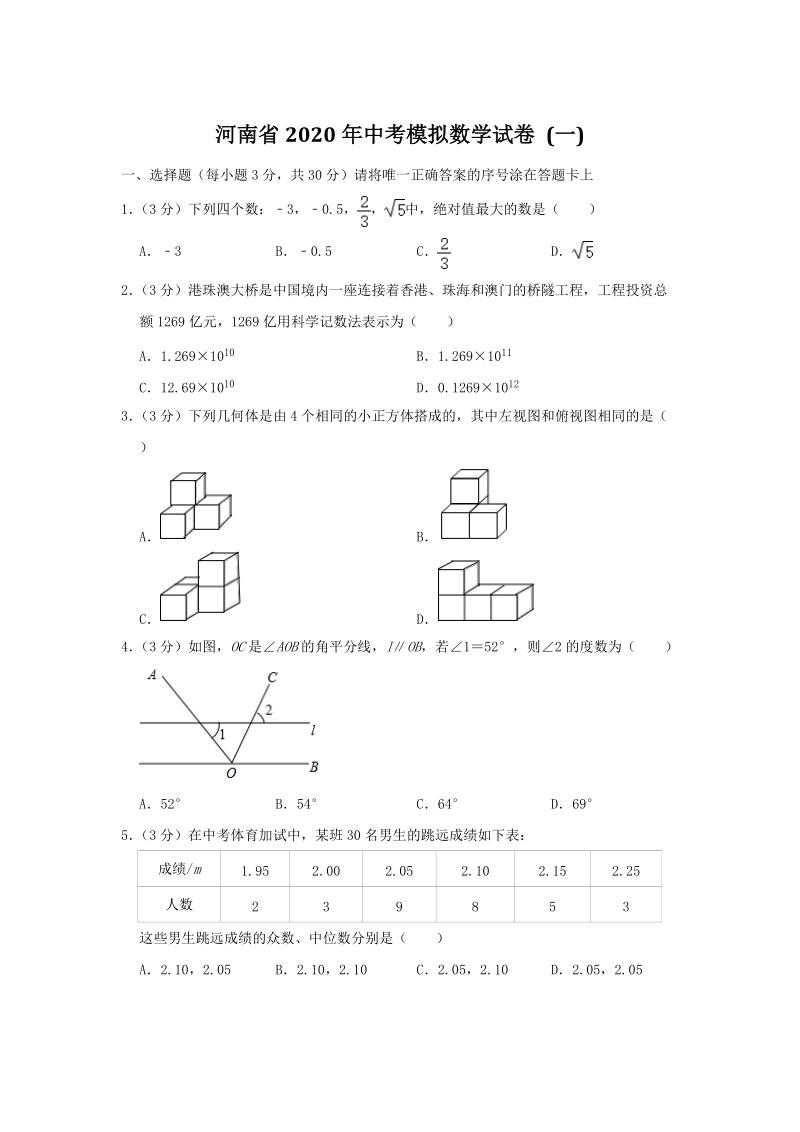
1、河南省2020年中考模拟数学试卷 (一)一、选择题（每小题3分，共30分）请将唯一正确答案的序号涂在答题卡上1（3分）下列四个数：3，0.5，中，绝对值最大的数是（）A3B0.5CD2（3分）港珠澳大桥是中国境内一座连接着香港、珠海和澳门的桥隧工程，工程投资总额1269亿元，1269亿用科学记数法表示为（）A1.2691010B1.2691011C12.691010D0.126910123（3分）下列几何体是由4个相同的小正方体搭成的，其中左视图和俯视图相同的是（）ABCD4（3分）如图，OC是AOB的角平分线，lOB，若152，则2的度数为（）A52B54C64D695（3分）在中考体育加试
2、中，某班30名男生的跳远成绩如下表：成绩/m1.952.002.052.102.152.25人数239853这些男生跳远成绩的众数、中位数分别是（）A2.10，2.05B2.10，2.10C2.05，2.10D2.05，2.056（3分）不等式组的解集在数轴上表示正确的是（）ABCD7（3分）如图，正比例函数yx的图象与一次函数yx+的图象交于点A，若点P是直线AB上的一个动点，则线段OP长的最小值为（）A1BCD28（3分）如图，点P是AOB内任意一点，且AOB40，点M和点N分别是射线OA和射线OB上的动点，当PMN周长取最小值时，则MPN的度数为（）A140B100C50D409（3分）
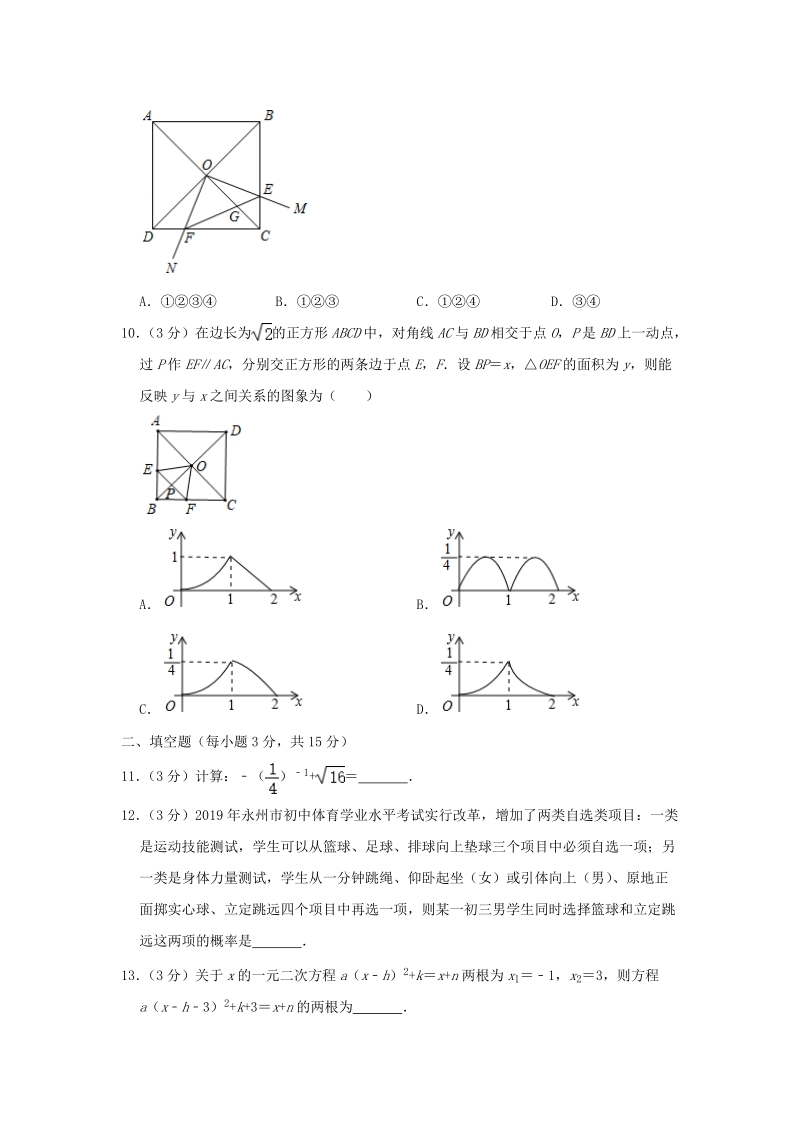
3、如图，在正方形ABCD中，点O是对角线AC、BD的交点，过点O作射线OM、ON分别交BC、CD于点E、F，且EOF90，OC、EF交于点G给出下列结论：COEDOF；OGEFGC；四边形CEOF的面积为正方形ABCD面积的；DF2+BE2OGOC其中正确的是（）ABCD10（3分）在边长为的正方形ABCD中，对角线AC与BD相交于点O，P是BD上一动点，过P作EFAC，分别交正方形的两条边于点E，F设BPx，OEF的面积为y，则能反映y与x之间关系的图象为（）ABCD二、填空题（每小题3分，共15分）11（3分）计算：（）1+ 12（3分）2019年永州市初中体育学业水平考试实行改革，增加了两
4、类自选类项目：一类是运动技能测试，学生可以从篮球、足球、排球向上垫球三个项目中必须自选一项；另一类是身体力量测试，学生从一分钟跳绳、仰卧起坐（女）或引体向上（男）、原地正面掷实心球、立定跳远四个项目中再选一项，则某一初三男学生同时选择篮球和立定跳远这两项的概率是 13（3分）关于x的一元二次方程a（xh）2+kx+n两根为x11，x23，则方程a（xh3）2+k+3x+n的两根为 14（3分）如图，7个腰长为1的等腰直角三角形（RtB1AA1，RtB2A1A2，RtB3A2A3）有一条腰在同一条直线上，设A1B2C1的面积为S1，A2B3C2的面积为S2，A3B4C3的面积为S3，则S1+S2
5、+S3+S4+S5+S6 15（3分）如图，RtABC中，ACB90，AC2，BC4，CD是ABC的中线，E是边BC上一动点，将BED沿ED折叠，点B落在点F处，EF交线段CD于点G，当DFG是直角三角形时，则CE 三、解答题（本大题共8个小题，满分75分）16（8分）先化简，再求值：，其中a是方程a2+a60的解17（9分）如图，在RtABC中，B90，BAC的平分线交BC于点D，以D为圆心，DB长为半径作作D（1）求证：AC是D的切线（2）设AC与D切于点E，DB1，连接DE，BF，EF当BAD 时，四边形BDEF为菱形；当AB 时，CDE为等腰三角形18（9分）设中学生体质健康综合评定成
6、绩为x分，满分为100分，规定：85x100为A级；75x85为B级；60x75为C级；x60为D级现随机抽取某中学部分学生的综合评定成绩，整理绘制成如下两幅不完整的统计图，请根据图中的信息，解答下列问题：（1）在这次调查中，一共抽取了 名学生，A级人数占本次抽取人数的百分比为 %；（2）补全条形统计图；（3）扇形统计图中C级对应的圆心角为 度；（4）若该校共有1000名学生，请你估计该校D级学生有多少名？19（9分）如图，某市郊外景区内一条笔直的公路a经过三个景点A、B、C，景区管委会又开发了风景优美的景点D，经测量景点D位于景点A的北偏东30方向8km处，位于景点B的正北方向，还位于景点C
7、的北偏西75方向上，已知AB5km（1）景区管委会准备由景点D向公路a修建一条距离最短的公路，不考虑其它因素，求出这条公路的长；（结果精确到0.1km）（2）求景点C与景点D之间的距离（结果精确到1km）（参考数据：1.73，2.24，sin53cos370.80，sin37cos530.60，tan531.33，tan370.75，sin38cos520.62，sin52cos380.79，tan380.78，tan521.28，sin750.97，cos750.26，tan753.73）20（9分）如图，直线y2x+6与反比例函数y（0）的图象交于点A（1，m），与x轴交于点B，平行于x轴
8、的直线yn（0n6）交反比例函数的图象于点M，交AB于点N，连接BM（1）求m的值和反比例函数的表达式；（2）观察图象，直接写出当x0时，不等式2x+60的解集；（3）当n为何值时，BMN的面积最大？最大值是多少？21（10分）某商场计划经销A，B两种新型节能台灯共50盏，这两种台灯的进价、售价如下表所示 A型B型进价（元/盏）4065售价（元/盏）60100（1）若该商场购进这批台灯共用去2500元，问这两种台灯各购进多少盏？（2）在每种台灯销售利润不变的情况下，若该商场销售这批台灯的总利润不少于1400元，问至少需购进B种台灯多少盏？（3）若该商场预计用不多于2600元的资金购进这批台灯，
9、其中A种台灯不超过30盏，为了打开B种台灯的销路，商场决定每售出一盏B种台灯，返还顾客现金a元（10a20），问该商场该如何进货，才能获得最大的利润？22（10分）（1）问题发现如图1，在RtABC和RtCDE中，ACBDCE90，CABCDE45，点D时线段AB上一动点，连接BE填空：的值为 ； DBE的度数为 （2）类比探究如图2，在RtABC和RtCDE中，ACBDCE90，CABCDE60，点D是线段AB上一动点，连接BE请判断的值及DBE的度数，并说明理由；（3）拓展延伸如图3，在（2）的条件下，将点D改为直线AB上一动点，其余条件不变，取线段DE的中点M，连接BM、CM，若AC2，
10、则当CBM是直角三角形时，线段BE的长是多少？请直接写出答案23（11分）如图，在平面直角坐标系中，抛物线yax2+bx+c的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点A、C的坐标分别为（1，0），（0，3），直线x1为抛物线的对称轴点D为抛物线的顶点，直线BC与对称轴相交于点E（1）求抛物线的解析式并直接写出点D的坐标；（2）点P为直线x1右方抛物线上的一点（点P不与点B重合）记A、B、C、P四点所构成的四边形面积为S，若SSBCD，求点P的坐标；（3）点Q是线段BD上的动点，将DEQ延边EQ翻折得到DEQ，是否存在点Q使得DEQ与BEQ的重叠部分图形为直角三角形？若存
11、在，请求出BQ的长，若不存在，请说明理由参考答案与试题解析一、选择题（每小题3分，共30分）请将唯一正确答案的序号涂在答题卡上1（3分）下列四个数：3，0.5，中，绝对值最大的数是（）A3B0.5CD【分析】根据绝对值的性质以及正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小判断即可【解答】解：|3|3，|0.5|0.5，|，|且0.53，所给的几个数中，绝对值最大的数是3故选：A2（3分）港珠澳大桥是中国境内一座连接着香港、珠海和澳门的桥隧工程，工程投资总额1269亿元，1269亿用科学记数法表示为（）A1.2691010B1.2691011C12.69101
12、0D0.12691012【分析】科学记数法的表示形式为a10n的形式，其中1|a|10，n为整数确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同当数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数【解答】解：1269亿126900000000，用科学记数法表示为1.2691011故选：B3（3分）下列几何体是由4个相同的小正方体搭成的，其中左视图和俯视图相同的是（）ABCD【分析】根据图形、找出几何体的左视图与俯视图，判断即可【解答】解：A、左视图第一层两个小正方形，俯视图第一层一个小正方形，故A不符合题意；B、左视图和俯视图相同，故B符合题意
13、；C、左视图第一层两个小正方形，俯视图第一层一个小正方形，故C不符合题意；D、左视图是一列两个小正方形，俯视图一层三个小正方形，故D不符合题意；故选：B4（3分）如图，OC是AOB的角平分线，lOB，若152，则2的度数为（）A52B54C64D69【分析】依据平行线的性质以及角平分线的定义，即可得到BOC64，再根据平行线的性质，即可得出2的度数【解答】解：lOB，1+AOB180，AOB128，OC平分AOB，BOC64，又lOB，且2与BOC为同位角，264，故选：C5（3分）在中考体育加试中，某班30名男生的跳远成绩如下表：成绩/m1.952.002.052.102.152.25人数2
14、39853这些男生跳远成绩的众数、中位数分别是（）A2.10，2.05B2.10，2.10C2.05，2.10D2.05，2.05【分析】中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数，众数是一组数据中出现次数最多的数据，注意众数可以不止一个【解答】解：由表可知，2.05出现次数最多，所以众数为2.05；由于一共调查了30人，所以中位数为排序后的第15人和第16人的平均数，即：2.10故选：C6（3分）不等式组的解集在数轴上表示正确的是（）ABCD【分析】分别解不等式进而得出不等式组的解集，进而得出答案【解答】解：，解得：x6，解得：x13，故不等式组的解集为：
15、6x13，在数轴上表示为：故选：B7（3分）如图，正比例函数yx的图象与一次函数yx+的图象交于点A，若点P是直线AB上的一个动点，则线段OP长的最小值为（）A1BCD2【分析】判断出OPAB时，OP最小，利用三角形的面积建立方程求解即可得出结论【解答】解：由得，A（2，3），由一次函数yx+，令y0，解得x2，（2，0），SAOBOB|yA|3，AB5，当OPAB时，OP最小，SAOBABOP最小，5OP最小3OP最小，故选：C8（3分）如图，点P是AOB内任意一点，且AOB40，点M和点N分别是射线OA和射线OB上的动点，当PMN周长取最小值时，则MPN的度数为（）A140B100C50D
16、40【分析】分别作点P关于OA、OB的对称点P1、P2，连P1、P2，交OA于M，交OB于N，PMN的周长P1P2，然后得到等腰OP1P2中，OP1P2+OP2P1100，即可得出MPNOPM+OPNOP1M+OP2N100【解答】解：分别作点P关于OA、OB的对称点P1、P2，连接P1P2，交OA于M，交OB于N，则OP1OPOP2，OP1MMPO，NPONP2O，根据轴对称的性质，可得MPP1M，PNP2N，则PMN的周长的最小值P1P2，P1OP22AOB80，等腰OP1P2中，OP1P2+OP2P1100，MPNOPM+OPNOP1M+OP2N100，故选：B9（3分）如图，在正方形A
17、BCD中，点O是对角线AC、BD的交点，过点O作射线OM、ON分别交BC、CD于点E、F，且EOF90，OC、EF交于点G给出下列结论：COEDOF；OGEFGC；四边形CEOF的面积为正方形ABCD面积的；DF2+BE2OGOC其中正确的是（）ABCD【分析】由正方形证明OCOD，ODFOCE45，COMDOF，便可得结论；证明点O、E、C、F四点共圆，得EOGCFG，OEGFCG，进而得OGEFGC便可；先证明SCOESDOF，便可；证明OEGOCE，得OGOCOE2，再证明OGACEF2，再证明BE2+DF2EF2，得OGACBE2+DF2便可【解答】解：四边形ABCD是正方形，OCOD
18、，ACBD，ODFOCE45，MON90，COMDOF，COEDOF（ASA），故正确；EOFECF90，点O、E、C、F四点共圆，EOGCFG，OEGFCG，OGEFGC，故正确；COEDOF，SCOESDOF，故正确；）COEDOF，OEOF，又EOF90，EOF是等腰直角三角形，OEGOCE45，EOGCOE，OEGOCE，OE：OCOG：OE，OGOCOE2，OCAC，OEEF，OGACEF2，CEDF，BCCD，BECF，又RtCEF中，CF2+CE2EF2，BE2+DF2EF2，OGACBE2+DF2，故错误，故选：B10（3分）在边长为的正方形ABCD中，对角线AC与BD相交于点
19、O，P是BD上一动点，过P作EFAC，分别交正方形的两条边于点E，F设BPx，OEF的面积为y，则能反映y与x之间关系的图象为（）ABCD【分析】分析，EF与x的关系，他们的关系分两种情况，依情况来判断抛物线的开口方向【解答】解：四边形ABCD是正方形，ACBD2，OBOD，当P在OB上时，即0x1，EFAC，BEFBAC，EF：ACBP：OB，EF2BP2x，yEFOP2x（1x）x2+x；当P在OD上时，即1x2，EFAC，DEFDAC，EF：ACDP：OD，即EF：2（2x）：1，EF42x，yEFOPx2+3x2，这是一个二次函数，根据二次函数的性质可知：二次函数的图象是一条抛物线，开
20、口方向取决于二次项的系数当系数0时，抛物线开口向上；系数0时，开口向下根据题意可知符合题意的图象只有选项B故选：B二、填空题（每小题3分，共15分）11（3分）计算：（）1+0【分析】直接利用负指数幂的性质以及二次根式的性质分别化简得出答案【解答】解：原式4+40故答案为：012（3分）2019年永州市初中体育学业水平考试实行改革，增加了两类自选类项目：一类是运动技能测试，学生可以从篮球、足球、排球向上垫球三个项目中必须自选一项；另一类是身体力量测试，学生从一分钟跳绳、仰卧起坐（女）或引体向上（男）、原地正面掷实心球、立定跳远四个项目中再选一项，则某一初三男学生同时选择篮球和立定跳远这两项的概
21、率是【分析】用A、B、C分别表示篮球、足球、排球向上垫球三个项目，用a、b、c、d分别表示一分钟跳绳、仰卧起坐（女）或引体向上（男）、原地正面掷实心球、立定跳远四个项目，画树状图展示所有9种等可能的结果数，找出某一初三男学生同时选择篮球和立定跳远这两项的结果数，然后根据概率公式求解【解答】解：用A、B、C分别表示篮球、足球、排球向上垫球三个项目，用a、b、c、d分别表示一分钟跳绳、仰卧起坐（女）或引体向上（男）、原地正面掷实心球、立定跳远四个项目，画树状图为：共有12种等可能的结果数，其中某一初三男学生同时选择篮球和立定跳远这两项的结果数为1，所以某一初三男学生同时选择篮球和立定跳远这两项的概
22、率故答案为13（3分）关于x的一元二次方程a（xh）2+kx+n两根为x11，x23，则方程a（xh3）2+k+3x+n的两根为2或6【分析】根据函数与方程的关系及函数平移的规律，变形要求的方程，利用平移规律可解【解答】解：由方程a（xh3）2+k+3x+n得a（xh3）2+kx+n3方程可看作左边是二次函数ya（xh3）2+k，右边是一次函数yx+n3根据平移知识，可知方程相当于关于x的一元二次方程a（xh）2+kx+n，左右两边都向右平移3个单位而方程的两根为x11，x23方程的两根为x12，x26故答案为2或614（3分）如图，7个腰长为1的等腰直角三角形（RtB1AA1，RtB2A1A
23、2，RtB3A2A3）有一条腰在同一条直线上，设A1B2C1的面积为S1，A2B3C2的面积为S2，A3B4C3的面积为S3，则S1+S2+S3+S4+S5+S6【分析】连接B1、B2、B3、B4点，显然它们共线且平行于AC1，依题意可知B1B2C1与C1AA1相似，求出相似比，根据三角形面积公式可得出S1，同理：B2B3：AA21：2，所以B2C2：C2A1：2，进而S2的值可求出，同样的道理，即可求出S3，S4S6的值，即可求解【解答】解：解：连接B1、B2、B3、B4n+1个边长为1的等腰三角形有一条边在同一直线上，11，211，31，3，连接B1、B2、B3点，显然它们共线且平行于AA
24、1易知S1，B2B3AA2，B2C2B3A2C2A，S2，同理可求，S3，S42，S5，S6，S1+S2+S3+S4+S5+S6，故答案为：15（3分）如图，RtABC中，ACB90，AC2，BC4，CD是ABC的中线，E是边BC上一动点，将BED沿ED折叠，点B落在点F处，EF交线段CD于点G，当DFG是直角三角形时，则CE1或【分析】分两种情形：如图1中，当DGF90时，作DHBC于H如图2中，当GDF90，作DHBC于H，DKFG于K【解答】解：如图1中，当DGF90时，作DHBC于H在RtACB中，ACB90，AC2，BC4，AB2，ADDB，CDAB，DHAC，ADDB，CHBH，D
25、HDGAC1，CG1，DCDB，DCBB，cosDCBcosB，CECGcosDCB如图2中，当GDF90，作DHBC于H，DKFG于K易证四边形DKEH是正方形，可得EHDH1，CHBH2，CE1，综上所述，满足条件的CE的值为1或三、解答题（本大题共8个小题，满分75分）16（8分）先化简，再求值：，其中a是方程a2+a60的解【分析】根据分式的减法和除法可以化简题目中的式子，然后由方程a2+a60可以求得a的值，然后将a的值代入化简后的式子即可解答本题，注意代入a的值必须使得原分式有意义【解答】解：，由a2+a60，得a3或a2，a20，a2，a3，当a3时，原式17（9分）如图，在Rt
26、ABC中，B90，BAC的平分线交BC于点D，以D为圆心，DB长为半径作作D（1）求证：AC是D的切线（2）设AC与D切于点E，DB1，连接DE，BF，EF当BAD30时，四边形BDEF为菱形；当AB+1时，CDE为等腰三角形【分析】（1）作DMAC于M，由角平分线的性质可得DMDB，由切线的判定可证AC是D的切线；（2）由菱形的性质可得BDBF，且BDDF，可证BDF是等边三角形，可得ADB60，即可求解；由切线的性质可得DEAC，由等腰直角三角形的性质可得CDDE，C45，可证ABBC+1【解答】证明：（1）如图1，作DMAC于M，B90，AD平分BAC，DMAC，DMDB，DB是D的半径
27、，AC是D的切线；（2）如图2，四边形BDEF是菱形，BDDEEFBF，BDDFDE，BDDFDEEFBF，BDF，DEF是等边三角形，ADBADE60，ABC90，BAD30，当BAD30时，四边形BDEF是菱形，故答案为：30；AC与D切于点E，DEAC，DEC是等腰三角形，且DEAC，DEEC，CEDC45，DCDE，ABC90，C45，BACC45，ABBC，BDDEEC1，DCx，ABBC+1，当AB+1时，CDE为等腰三角形，故答案为：+118（9分）设中学生体质健康综合评定成绩为x分，满分为100分，规定：85x100为A级；75x85为B级；60x75为C级；x60为D级现随机
28、抽取某中学部分学生的综合评定成绩，整理绘制成如下两幅不完整的统计图，请根据图中的信息，解答下列问题：（1）在这次调查中，一共抽取了50名学生，A级人数占本次抽取人数的百分比为24%；（2）补全条形统计图；（3）扇形统计图中C级对应的圆心角为72度；（4）若该校共有1000名学生，请你估计该校D级学生有多少名？【分析】（1）根据B级的人数和所占的百分比求出抽取的总人数，再用A级的人数除以总数即可求出；（2）用抽取的总人数减去A、B、D的人数，求出C级的人数，从而补全统计图；（3）用360度乘以C级所占的百分比即可求出扇形统计图中C级对应的圆心角的度数；（4）用D级所占的百分比乘以该校的总人数，即
29、可得出该校D级的学生数【解答】解：（1）在这次调查中，一共抽取的学生数是：2448%50（人），100%24%；故答案为：50，24；（2）等级为C的人数是：501224410（人），补图如下：（3）扇形统计图中C级对应的圆心角为36072；故答案为：72；（4）根据题意得：100080（人），答：该校D级学生有80人19（9分）如图，某市郊外景区内一条笔直的公路a经过三个景点A、B、C，景区管委会又开发了风景优美的景点D，经测量景点D位于景点A的北偏东30方向8km处，位于景点B的正北方向，还位于景点C的北偏西75方向上，已知AB5km（1）景区管委会准备由景点D向公路a修建一条距离最短的公
30、路，不考虑其它因素，求出这条公路的长；（结果精确到0.1km）（2）求景点C与景点D之间的距离（结果精确到1km）（参考数据：1.73，2.24，sin53cos370.80，sin37cos530.60，tan531.33，tan370.75，sin38cos520.62，sin52cos380.79，tan380.78，tan521.28，sin750.97，cos750.26，tan753.73）【分析】过点D作DEAC于点E，过点A作AFDB，交DB的延长线于点F，求DE的问题就可以转化为求DBE的度数或三角函数值的问题RtDCE中根据三角函数就可以求出CD的长【解答】解：（1）如图，
31、过点D作DEAC于点E，过点A作AFDB，交DB的延长线于点F，在RtDAF中，ADF30，AFAD84，DF，在RtABF中BF3，BDDFBF43，sinABF，在RtDBE中，sinDBE，ABFDBE，sinDBE，DEBDsinDBE（43）3.1（km），景点D向公路a修建的这条公路的长约是3.1km；（2）由题意可知CDB75，由（1）可知sinDBE0.8，所以DBE53，DCB180755352，在RtDCE中，sinDCE，DC4（km），景点C与景点D之间的距离约为4km20（9分）如图，直线y2x+6与反比例函数y（0）的图象交于点A（1，m），与x轴交于点B，平行于x
32、轴的直线yn（0n6）交反比例函数的图象于点M，交AB于点N，连接BM（1）求m的值和反比例函数的表达式；（2）观察图象，直接写出当x0时，不等式2x+60的解集；（3）当n为何值时，BMN的面积最大？最大值是多少？【分析】（1）求出点A的坐标，利用待定系数法即可解决问题；（2）结合函数图象找到直线在双曲线下方对应的x的取值范围；（3）构建二次函数，利用二次函数的性质即可解决问题【解答】解：（1）直线y2x+6经过点A（1，m），m21+68，A（1，8），反比例函数经过点A（1，8），k8，反比例函数的解析式为y；（2）不等式2x+60的解集为0x1；（3）由题意，点M，N的坐标为M（，n）
33、，N（，n），0n6，0，0SBMN|MN|yM|（n3）2+，n3时，BMN的面积最大，最大值为21（10分）某商场计划经销A，B两种新型节能台灯共50盏，这两种台灯的进价、售价如下表所示 A型B型进价（元/盏）4065售价（元/盏）60100（1）若该商场购进这批台灯共用去2500元，问这两种台灯各购进多少盏？（2）在每种台灯销售利润不变的情况下，若该商场销售这批台灯的总利润不少于1400元，问至少需购进B种台灯多少盏？（3）若该商场预计用不多于2600元的资金购进这批台灯，其中A种台灯不超过30盏，为了打开B种台灯的销路，商场决定每售出一盏B种台灯，返还顾客现金a元（10a20），问该商
34、场该如何进货，才能获得最大的利润？【分析】（1）首先设该商场购进A种台灯x盏，购进B种台灯（50x）盏，然后根据题意，即可得方程，解方程即可求得答案；（2）设至少需购进B种台灯x盏，然后由该商场销售这批台灯的总利润不少于1400元，即可得一元一次不等式35y+20（50y）1400，解此不等式即可求得答案；（3）首先设该商场购进A种台灯m盏，由该商场预计用不多于2600元的资金购进这批台灯，可通过不等式组求得m的取值范围，然后求得该商场获得的总利润与该商场购进A种台灯的盏数的一次函数，由10a20，根据一次函数的增减性即可求得答案【解答】解：（1）设该商场购进A种台灯x盏，购进B种台灯（50x
35、）盏，由题意得：40x+65（50x）2500，解得：x30，该商场购进A种台灯30盏，购进B种台灯20盏（2）设购进B种台灯y盏，由题意得：35y+20（50y）1400，解得：y，y的最小整数解为27，至少需购进B种台灯27盏；（3）设该商场购进A种台灯m盏，由题意得：40m+65（50m）2600，解得：m26，26m30，设该商场获得的总利润为w元，则w20m+（35a）（50m）（a15）m+175050a，10a20，当10a15时，m26，即购进A种台灯26盏，购进B种台灯24盏，该商场获得的总利润最大，当15a20时，m30，即购进A种台灯30盏，购进B种台灯20盏，该商场获得
36、的总利润最大22（10分）（1）问题发现如图1，在RtABC和RtCDE中，ACBDCE90，CABCDE45，点D时线段AB上一动点，连接BE填空：的值为1； DBE的度数为90（2）类比探究如图2，在RtABC和RtCDE中，ACBDCE90，CABCDE60，点D是线段AB上一动点，连接BE请判断的值及DBE的度数，并说明理由；（3）拓展延伸如图3，在（2）的条件下，将点D改为直线AB上一动点，其余条件不变，取线段DE的中点M，连接BM、CM，若AC2，则当CBM是直角三角形时，线段BE的长是多少？请直接写出答案【分析】（1）由直角三角形的性质可得ABC45，可得DBE90，通过证明AC
37、DBCE，可得的值；（2）通过证明ACDBCE，可得的值，CBECAD60，即可求DBE的度数；（3）分点D在线段AB上和BA延长线上两种情况讨论，由直角三角形的性质可证CMBM，即可求DE2，由相似三角形的性质可得ABE90，BEAD，由勾股定理可求BE的长【解答】解：（1）ACB90，CAB45ABCCAB45ACBC，DBEABC+CBE90ACBDCE90，ACDBCE，且CABCDE45，ACDBCE故答案为：1，90（2），DBE90理由如下：ACBDCE90，CABCDE60，ACDBCE，CEDABC30tanABCtan30ACBDCE90，CABCDE60，RtACBRtD
38、CE，且ACDBCEACDBCE，CBECAD60DBEABC+CBE90（3）若点D在线段AB上，如图，由（2）知：，ABE90BEADAC2，ACB90，CAB90AB4，BC2ECDABE90，且点M是DE中点，CMBMDE，且CBM是直角三角形CM2+BM2BC2（2）2，BMCMDE2DB2+BE2DE2，（4AD）2+（AD）224AD+1BEAD3+若点D在线段BA延长线上，如图同理可得：DE2，BEADBD2+BE2DE2，（4+AD）2+（AD）224，AD1BEAD3综上所述：BE的长为3+或323（11分）如图，在平面直角坐标系中，抛物线yax2+bx+c的图象与x轴交于
39、A、B两点（点A在点B的左边），与y轴交于点C，点A、C的坐标分别为（1，0），（0，3），直线x1为抛物线的对称轴点D为抛物线的顶点，直线BC与对称轴相交于点E（1）求抛物线的解析式并直接写出点D的坐标；（2）点P为直线x1右方抛物线上的一点（点P不与点B重合）记A、B、C、P四点所构成的四边形面积为S，若SSBCD，求点P的坐标；（3）点Q是线段BD上的动点，将DEQ延边EQ翻折得到DEQ，是否存在点Q使得DEQ与BEQ的重叠部分图形为直角三角形？若存在，请求出BQ的长，若不存在，请说明理由【分析】（1）利用抛物线的对称性得到B（3，0），则设交点式为ya（x+1）（x3），把C（0，3）
40、代入求出a即可得到抛物线解析式，然后把解析式配成顶点式即可得到D点坐标；（2）设P（m，m22m3），先确定直线BC的解析式yx3，再确定E（1，2），则可根据三角形面积公式计算出SBDCSBDE+SCDE3，然后分类讨论：当点P在x轴上方时，即m3，如图1，利用SSPAB+SCABSBCD得到2m24m；当点P在x轴下方时，即1m3，如图2，连结OP，利用SSAOC+SCOP+SPOBSBCD得到m2+m+6，再分别解关于m的一元二次方程求出m，从而得到P点坐标；（3）存在直线x1交x轴于F，利用两点间的距离公式计算出BD2，分类讨论：如图3，EQDB于Q，证明RtDEQRtDBF，利用相似比可计算出DQ，则BQBDDQ；如图4，EDBD于H，证明RtDEQHRtDBF，利用相似比计算出DH，EH，在
