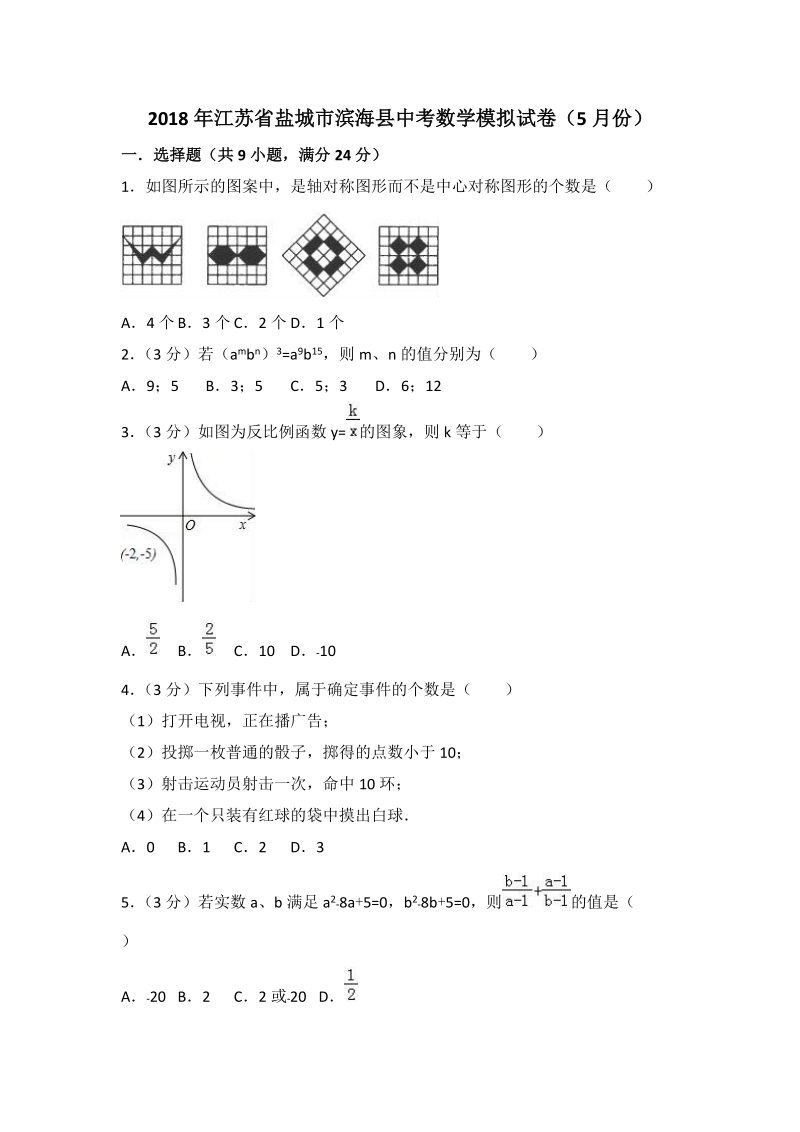
1、2018 年江苏省盐城市滨海县中考数学模拟试卷（5 月份）一选择题（共 9 小题，满分 24 分）1如图所示的图案中，是轴对称图形而不是中心对称图形的个数是（ ）A4 个 B3 个 C2 个 D1 个2 （3 分）若（a mbn） 3=a9b15，则 m、n 的值分别为（ ）A9 ；5 B3；5 C5；3 D6；123 （3 分）如图为反比例函数 y= 的图象，则 k 等于（ ）A B C10 D 104 （3 分）下列事件中，属于确定事件的个数是（ ）（1）打开电视，正在播广告；（2）投掷一枚普通的骰子，掷得的点数小于 10；（3）射击运动员射击一次，命中 10 环；（4）在一个只装有红球的
2、袋中摸出白球A0 B1 C2 D35 （3 分）若实数 a、b 满足 a28a+5=0，b 28b+5=0，则 的值是（ ）A 20 B2 C2 或20 D6 （3 分）如图是某几何体的三视图，根据图中数据，求得该几何体的体积为（ ）A60 B70 C90 D1607 （3 分）如图所示，MN 是O 的直径，作 ABMN，垂足为点 D，连接AM，AN，点 C 为 上一点，且 = ，连接 CM，交 AB 于点 E，交 AN 于点F，现给出以下结论：AD=BD；MAN=90 ； = ；ACM+ ANM=MOB ；AE= MF来源:学科网其中正确结论的个数是（ ）A2 B3 C4 D58 （3 分）
3、已知点 M（n ，n ）在第二象限，过点 M 的直线 y=kx+b（0k1）分别交 x 轴、y 轴于点 A， B，过点 M 作 MNx 轴于点 N，则下列点在线段 AN的是（ ）A （k 1）n，0） B （ k+ ）n，0） ） C （ ，0） D （k +1）n，0 ）9 （3 分）已知二次函数 y=ax2+bx+c（a0）图象如图所示，下列结论：abc0；2ab0；b 2（a+c ） 2；点（3 ，y 1） ， （1，y 2）都在抛物线上，则有 y1y 2其中正确的结论有（ ）A4 个 B3 个 C2 个 D1 个二填空题（共 7 小题，满分 21 分，每小题 3 分）10 （3 分）函
4、数 中，自变量 x 取值范围是 11 （3 分）在小学阶段，我们知道可以将一个分数拆分成两个分数的和（差）的形式，例如 ， = 类似地，我们也可以把一个较复杂的分式拆分成两个较简单，并且分子次数小于分母次数的分式的和或者差的形式例如 = ，仿照上述方法，若分式 可以拆分成 的形式，那么 （B+1） （A+1） = 12 （3 分）如图所示的是某班全体学生在课外活动中参加各种兴趣小组的情况统计图，那么从这个班中任意挑选一人，恰为参加美术兴趣小组的学生的概率是 %13 （3 分）科学家发现一种病毒的直径为 0.000104 米，用科学记数法表示为 米14 （3 分）某兴趣小组成员的年龄统计（不完整
5、）如下表所示，已知他们的平均年龄是 14.5 岁，那么年龄为 14 岁的人数是 年龄/岁 13 14 15 16人数 1 5 115 （3 分）如图，将一块实心三角板和实心半圆形量角器按图中方式叠放，三角板一直角边与量角器的零刻度线所在直线重合，斜边与半圆相切，重叠部分的量角器弧对应的圆心角（AOB）为 120，BC 的长 为 2 ，则三角板和量角器重叠部分的面积为 16 （3 分）如图，已知ABC 内接于O ，CD 是O 的切线与半径 OB 的延长线交于点 D， A=30 ，求 BCD 的度数三解答题（共 8 小题，满分 50 分）17 （8 分）计算：4cos45 +（ ） 0+（1） 2
6、18 （8 分）先化简，再求值：（ + ） ，其中 x= 319 （8 分）如图，O A， OB 是O 的两条半径，OAOB ，C 是半径 OB 上的一动点，连接 AC 并延长交 O 于 D，过点 D 作直线交 OB 延长线于 E，且DE=CE，已知 OA=8（1）求证：ED 是O 的切线；（2）当A=30时，求 CD 的长20 （8 分）如图，已知直线 y=2x，经过点 P（ 2，a） ，点 P 关于 y 轴的对称点P在反比例函数 y= （k 0）的图象上（1）求点 P的坐标；（2）求反比例函数的解析式，并直接写出当 y1 时自变量 x 的取值范围21 （8 分）诸暨某童装专卖店在销售中发现
7、，一款童装每件进价为 80 元，销售价为 120 元时，每天可售出 20 件，为了迎接“五一”国际劳动节，商店决定采取适当的降价措施，以扩大销售量，增加利润，经市场调查发现，如果每件童装降价 1 元，那么平均可多售出 2 件（1）设每件童装降价 x 元时，每天可销售 件，每件盈利 元；（用 x 的代数式表示）（2）每件童装降价多少元时，平均每天赢利 1200 元（3）要想平均每天赢利 2000 元，可能吗？请说明理由22 （10 分）如图，海中有一小岛 P，在距小岛 P 的 海里范围内有暗礁，一轮船自西向东航行，它在 A 处时测得小岛 P 位于北偏东 60，且 A、P 之间的距离为 32 海里
8、，若轮船继续向正东方向航行，轮船有无触礁危险？请通过计算加以说明 如果有危险，轮船自 A 处开始至少沿东偏南多少度方向航行，才能安全通过这一海域？23如图，一小球沿与地面成一定角度的方向飞出，小球的飞行路线是一条抛物线如果不考虑空气阻力，小球的飞行高度 y（单位：m）与飞行时间 x（单位：s）之间具有函数关系 y=5x2+20x，请根据要求解答下列问题：（1）在飞行过程中，当小球的飞行高度为 15m 时，飞行时间是多少？（2）在飞行过程中，小球从飞出到落地所用时间是多少？（3）在飞行过程中，小球飞行高度何时最大？最大高度是多少？24如图 1，正方形 ABCD 的边长为 4，把三角板的直角顶点放
9、置 BC 中点 E 处，三角板绕点 E 旋转，三角板的两边分别交边 AB、 CD 于点 G、F（1）求证：GBEGEF（2）设 AG=x，GF=y ，求 Y 关于 X 的函数表达式，并写出自变量取值范围（3）如图 2，连接 AC 交 GF 于点 Q，交 EF 于点 P当AGQ 与CEP 相似，求线段 AG 的长2018 年江苏省盐城市滨海县中考数学模拟试卷（5 月份）参考答案与试题解析一选择题（共 9 小题，满分 24 分）1【解答】解：第一个图案是轴对称图形，而不是中心对称图形符合题意；其余三个图案既是中心对称图形，又是轴对称图形不符合题意故是轴对称图形而不是中心对称图形的个数是 1 个故选
10、：D2【解答】解：（a mbn） 3=a9b15，a 3mb3n=a9b15，3m=9 ，3n=15，m=3，n=5，故选：B3【解答】解：将点（2， 5）代入 y= ，得 k=10故选：C4【解答】解：（1） （3）属于随机事件；（4）是不可能事件，属于确定事件；（2）是必然事件，属于确定事件；故属于确定事件的个数是 2，故选：C5【解答】解：当 a=b 时，原式 =2；当 ab 时，根据实数 a、b 满足 a28a+5=0，b 28b+5=0，即可看成 a、b 是方程 x28x+5=0 的解，a +b=8，ab=5则 = ，把 a+b=8，ab=5 代入得：来源: 学*科*网 Z*X*X*
11、K=20综上可得 的值为 2 或 20故选：C6【解答】解：观察三视图发现该几何体为空心圆柱，其内圆半径为 3，外圆半径为 4，高为 10，所以其体积为 10（4 232）=70，故选：B7【解答】解：MN 是O 的直径，ABMN，AD=BD， = ，MAN=90（正确） = ， = = ，ACM + ANM=MOB（正确）MAE=AME，AE=ME， EAF=AFM，AE=EF，AE= MF（正确） 正确的结论共 5 个故选：D8【解答】解：如图所示，过 M 作 MCy 轴于 C，M（ n，n ） ，MNx 轴于点 N，C （0，n） ，N（n，0） ，把 M（ n，n ）代入直线 y=kx
12、+b，可得 b=nkn，y=kxn（1 +k） ，令 x=0，则 y=n（1+k ） ，即 B（0， n（1+k） ） ，n（1+k ） n，n（1+k ） n，令 y=0，则 0=kxn（1+k） ，解得 x= =n（ ） ，即 A（n（ ） ，0） ，0k 1，n0 ，n（ ） n（1+k）n，点（k+1）n，0）在线段 AN 上故选：D9【解答】解：抛物线开口向上，a 0 ， 0，b0，抛物线交 y 轴于负半轴，c0，abc0，故正确， 1，a0，b2a ，2ab0，故正确，x=1 时，y0 ，a +b+c0，a +cb，x=1 时，y 0，a b+c0，a +cb，b 2（a+c ）
13、2，故正确，点（3，y 1） ， （1，y 2）都在抛物线上，观察图象可知 y1y 2，故错误故选：B二填空题（共 7 小题，满分 21 分，每小题 3 分）10【解答】解：根据题意，得 x40，解得 x4故答案为 x411【解答】解：= += ， = ， = ，则 ，解得： ，所以（B+1） （A+1） =32= ，故答案为： 12【 解答】解：观察这个图可知：标有一等奖区域的面积占总圆面面积的 10%故答案为：1013【解答】解：0.000104=1.04 104，故答案为：1.0410 414【解答】解：设年龄为 14 岁的人数是 x，则（13+14x+155+16 ）（1+x+5+1）
14、=14.5，解得 x=5故答案为：515【 解答】解：AOB=120，BOC=60OCB=90，BC=2 ，OC= =2，OB=4，重叠部分的面积= + 22= +2 ，故答案为： +2 16【解答】解：如图，连接 OC，CD 是O 的切线，OCCD，OCD=90，A=30，COB=2A=60，OC=OB，OBC 是等边三角形，OCB=60，BCD=90OCB=30三解答题（共 8 小题，满分 50 分）17【解答】解：原式=4 2 +1+1=218【解答】解：原式= = ，当 x= 3 时，原式= 19【解答】 （1）证明：如图连接 ODOA=OD，A=ODA ，OAOB，AOB=90，A+
15、ACO=90，ED=EB，EDB= EBD=ACO ，ODA+ EDC=90，ODDE，DE 是O 的切线（2）在 Rt AOC 中，OA=8，A=30 ，OC =OAtan30= ，OA=OD，ODA=A=30，DOA=120，DOC=30， 来源:学科网 ZXXKDOC=ODC=30 ，来源:学_ 科_ 网CD=OC= 20【解答】解：（1）将 P（2，a）代入 y=2x 得 a=2（2）=4，P（2，4） ；（2）将 P（2，4）代入 y= 得 4= ，解得 k=8，反比例函数的解析式为 y= ，当 y1 时自变量 x 的取值范围是 x8来源 :Zxxk.Com21【解答】解：（1）设每
16、件童装降价 x 元时，每天可销售 20+2x 件，每件盈利40x 元，故答案为：（20+2x） ， （40 x） ；（2）根据题意，得：（20+2x ） （40 x）=1200解得：x 1=20， x2=10答：每件童装降价 20 元或 10 元，平均每天赢利 1200 元；（3）不能，（20+2x） （40x）=2000 此方程无解，故不可能做到平均每天盈利 2000 元22【解答】解：过 P 作 PBAM 于 B，在 RtAPB 中，PAB=30，PB= AP= 32=16 海里，1616 ，故轮船有触礁危险为了安全，应该变航行方向，并且保证点 P 到航线的距离不小于暗礁的半径 16海里，
17、即这个距离至少为 16 海里，设安全航向为 AC，作 PDAC 于点 D，由题意得，AP=32 海里， PD=16 海里，sin PAC= = = ，在 RtPAD 中，PAC=45，BAC=PACPAB=45 30=15答：轮船自 A 处开始至少沿南偏东 75度方向航行，才能安全通过这一海域23【解答】解：（1）当 y=15 时，15=5x2+20x，解得，x 1=1， x2=3，答：在飞行过程中，当小球的飞行高度为 15m 时，飞行时间是 1s 或 3s；（2）当 y=0 时，0 5x2+20x，解得，x 1=0， x2=4，4 0=4，在飞行过程中，小球从飞出到落地所用时间是 4s；（3
18、）y= 5x2+20x=5（x 2） 2+20，当 x=2 时，y 取得最大值，此时，y=20 ，答：在飞行过程中，小球飞行高度第 2s 时最大，最大高度是 20m24【解答】解：如图 1，延长 FE 交 AB 的延长线于 F，点 E 是 BC 的中点，BE=CE=2，四边形 ABCD 是正方形，ABCD，F=CFE，在BEF和 CEF 中， ，BEF CEF，BF=CF，EF=EF，GEF=90，GF=GF，BGE=EGF，GBE=GEF=90， GBEGEF；（2）FEG=90，BEG+CEF=90 ，BEG+BGE=90，BGE=CEF ，EBG=C=90，BEGCFE， ，由（1）知，
19、BE=CE=2，AG=x，BG=4x ， ，CF= ，由（1）知，BF= CF= ，由（1）知，GF=GF=y ，y=GF=BG+BF=4x+当 CF=4 时，即： =4，x=3， （0x 3 ） ，即：y 关于 x 的函数表达式为 y=4x+ （0x3） ；（3）AC 是正方形 ABCD 的对角线，BAC=BCA=45，A GQ 与CEP 相似，AGQ CEP，AGQ= CEP，由（2）知，CEP=BGE ，AGQ= BGE，由（1）知，BGE=FGE，AGQ= BGQ=FGE，AGQ +BGQ +FGE=180，BGE=60，BEG=30，在 RtBEG 中， BE=2，BG= ，AG=ABBG=4 ，AGQ CPE，AQG= CEP，CEP=BGE=FGE，AQG= FGE，EGAC，BEGBCA ， ， ，BG=2，AG=ABBG=2，即：当AGQ 与CEP 相似，线段 AG 的长为 2 或 4
