1、精锐教育1对3辅导讲义学员姓名： 学科教师：年 级： 辅导科目：授课日期时 间主 题第20讲-一模复习（三）18、25题学习目标1 掌握翻折旋转的图形特征；2 .掌握相似基本图形中的相似三角形和各种比例式；3 通过观察了解因动点产生的相似三角形问题的特点，熟悉解题方法， 掌握“动中取静，以静窥动”的解题策略；4 培养学生对图形的直觉能力以及从变化中看到不变实质的数学洞察力；教学内容针对上节课的内容进行复习和提问，检查和讲解上次课的课后巩固作业 18题常考题型解析【题型一】翻折问题；性质： 翻折前后两个图形全等：边相等，角相等 折痕垂直平分对应点的连线 学会找等腰画图： 已知折痕：过对应点做折痕
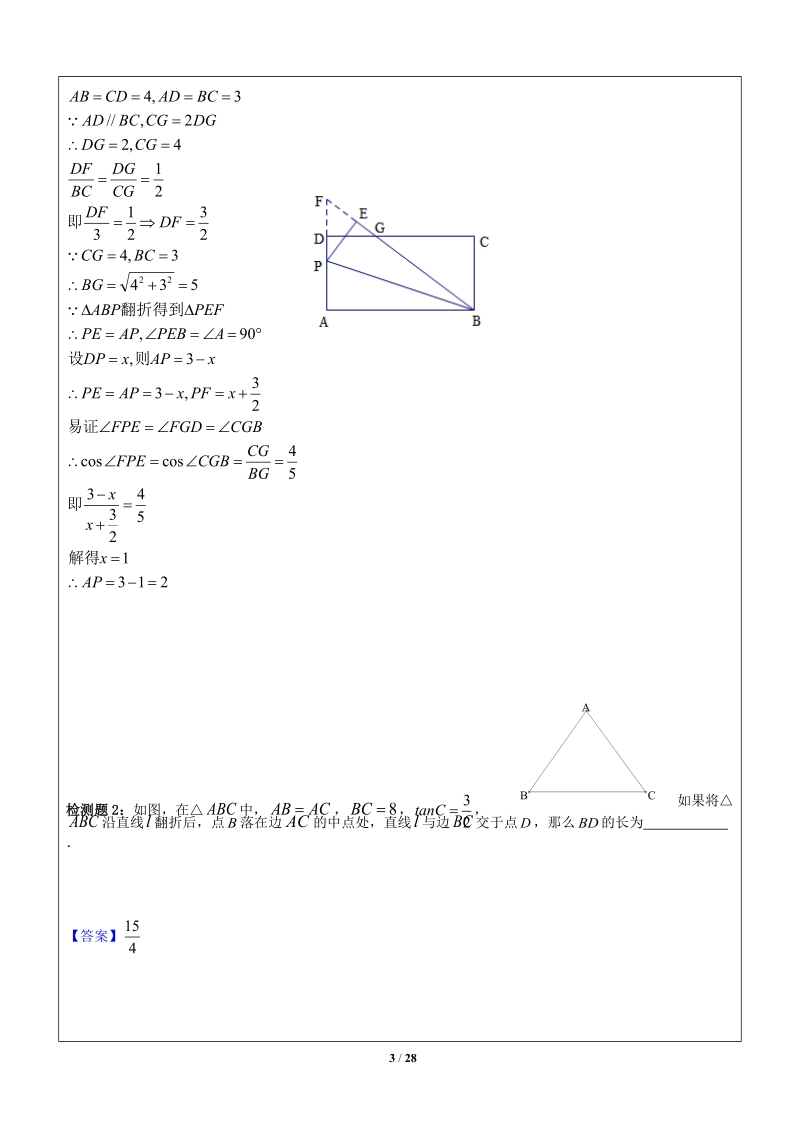
2、的垂线并延长 已知对应点：做对应点连线的垂直平分线例题：如图，在梯形中，,点是边上一点，如果把沿折痕向上翻折，点恰好与点重合，那么为 。 【答案】【解析】把沿折痕向上翻折，点恰好与点重合在直角梯形中，作,则,作的角平分线交于点，联结，过点作的垂线交的延长线于点。由翻折可知，,由作图易得，在中，由勾股定理易得,检测题1：如图，在矩形中，,，点是边上的一点，联结，将沿着所在直线翻折得到，点落在点处，边与边相交于点，如果，那么的长是 【答案】2【解析】检测题2：如图，在中，如果将沿直线翻折后，点落在边的中点处，直线与边交于点，那么的长为 【答案】在RTEDH中，勾股解出BD=x=【题型二】旋转问题；
3、旋转三要素 旋转中心 旋转方向：顺时针；逆时针 旋转角度性质： 旋转前后两个图形全等：边相等，角相等 会找新的相似：以旋转角为顶角的两个等腰三角形相似注意题目中的暗示： 旋转后点落在 边上、直线上、射线上画图： 点的旋转 图形的旋转：可以把图形的旋转转化为点的旋转，从而画圆例题：把边长为的等边三角形ABC绕着点C旋转90度后，点A落在点处，那么线段的长等于 cm。 【答案】 【解析】画图（如下图），分顺时针和逆时针两个情况，根据图象可以的， ，则。 检测题1：如图，中，,于点,将绕点逆时针旋转，旋转角的大小与相等，如果点旋转后分别落在点的位置，那么的正切值是 。【答案】【解析】【方法一】【方法
4、二】检测题2：如图，已知中，,于点，点在上，且,联结，将绕点旋转，得到（点、分别与点、对应），联结,当点落在上时（不与重合），如果，那么的长为 。【答案】【解析】 易得 当点落在上时（不与重合）, 易得等腰等腰 ，【题型三】面积例题：如图10,菱形形内两点，满足,，若四边形的面积是菱形面积的，则 .【答案】【解析】联结AC,BD交于点O，延长BM交AD于H点. 由菱形性质和已知条件，易得M、N在AC上， 因为, 所以OC=5OM 设OM=1，则OC=5 所以检测题1：如图，且过的重心，分别和交于点，点是线段上的一点，的延长线和交于点，如果，那么：的值是 。【答案】【解析】，且过的重心又过点和点
5、作的垂线，垂足分别为则检测题2：如图3，在平行四边形中，,点分别在边上，点是边的中点，,过点分别作，垂足分别为，那么的值是 。【答案】【解析】设过作，过作同理25题常考题型解析题型一、等腰三角形的分类讨论思路点拨：出现概率较高题型，重点。解决此类问题主要通过两个方面解决： 1.一方面从边方面入手，将此三角形的三边用的表达式表示，根据腰相等建 立方程求出线段长度（优点：方法简单，易理解；缺点：计算量偏大，易出错）； 2.另一方面从角方面入手，利用等腰产生的底角相等转化出其他的角度关系或边长关 系进而建立方程求出线段的长度（优点：计算量偏小，易计算，缺点：此方法对于 孩子的分析能力要求较高，适合一
6、部分程度较好的学生）。例题：已知：如图8，中，点在边上（不与点、重合），点在边的延长线上，点在线段上，设。（1）若点恰好是的中点，求线段的长；（2）若，求关于的函数关系式，并写出它的定义域；（3）当是以为腰的等腰三角形时，求线段的长。【答案】（1）；（2）；（3）或5。【解析】（1）（2）过点做垂直于点，易得： ， 显然，, 过点做平行，延长交于点，易得： 又 (3) 当是以为腰的等腰三角形，有以下两种情况：当时，是的角平分线，由得，解得。当时，即第一问的情况，。综上：或者。检测题1：如图9，在直角三角形中，,，点是的中点，当以点为旋转中心旋转时，交的延长线于点，交边于点，交线段于点。（1）当
7、时，求线段的长；（2）设，试求与之间的函数解析式，并写出定义域；（3）如果是以为腰的等腰三角形，请直接写出线段的长。【答案】（1）（2）；（3） 时，；，。【解析】（1） 在直角三角形中，易得，过点O作交于点，由为的中位线，易得，当时，为的中位线，易得（2） ，所以，即，过点作，易得，又，化简得：（3） 当时，过点作，易得，代入第二问解析式，化简得：，当，易得，又，即，化简整理得：即，（舍），综上，当，；当时，题型二、动点产生的相似综合思路点拨：1.首先寻找题目中特殊的条件和不变的量，并找出由条件引发的一些相等角、相 等线 段等特殊条件；（挖掘题目中的隐藏条件） 2.然后注意分类讨论，先找到对
8、应相等的角，再决定分类讨论情况： 3.相似三角形的边如果能直接求出列等式最好，如果不能求出，注意转化相似（是 否产生新的相似、等腰、平行四边形等更特殊的条件）.例题：如图，在中，是斜边上的中线，点是延长线上的一动点，过点作，交延长线于点，设，。（1）求关于的函数关系式及定义域；（2）过点作交于，当和相似时，求的值。【参考教法】：一题目看完了吧！你来找一下题目中由哪些不变的量或者是比较特殊的条件，找找看：1. 点、的位置情况？提示：点为边的中点，点是延长线上的一动点；2.题目中是否有垂直？提示：；二求解函数关系式，太简单了，你自己计算吧！提示：求解函数关系式式，注意构造基本图形使得与有关系，第（
9、1）问过点作，则/，则形成A字型基本图形；三当和相似时：1.是否有相等的角？提示：；2.是否需要分类讨论？提示：没有指定对应边，应该需要；3.如需要分类讨论，则分哪几种？提示：因为，则所以分两个情况讨论：当时，在中，；，；当时，在中，4.由于题目中出现很多直角，用哪个方法计算比较好？提示：锐角三角比。【满分解答】（1）在中， ， 是斜边上的中线， ； ，定义域为 （2） 当和相似时，可得和也相似 分两种情况：当时，在中，解得； 当时，在中， ，解得 综合，或10检测题1：如图，在梯形中，与相交于点，点在的延长线上，. 已知.（1）求证：；（2）设，求与之间的函数解析式，并写出定义域；（3）如果
10、，求的长.【答案】（1）略；（2）；（3）.【解析】(1)又且可得(2)分别过点作的垂线，垂足为点在中，在中，可证由(1)可知即(3)可得此时梯形为等腰梯形即解得，即题型三、动点产生的直角三角形问题思路点拨：当判断一个动三角形为直角三角形时，首先注意分类讨论。其次就是利用这个直 角来求解线段长度或角度问题，可以考虑用一下两种方法： 1.直角三角形的基本性质，包括锐角互余关系，三边勾股关系，斜中定理关系， 以及30角性质等； 2.利用产生的直角，利用锐角三角比或构造一线三直角利用相似关系来解题。例题：已知，如图9，在菱形中，联结,点是射线上的一个动点（点不与第重合），联结，与对角线相交于点，联结
11、.（1） 求证：；（2） 当点在线段上时，设，求与的函数解析式，并写出定义域；（3） 当点在线段延长线上时，若是直角三角形，求线段的长。【答案】（1）略；（2）（3）的长为或.【解析】（1） 在菱形中（2） 联结，交于点过点作（3） 1.当时在中，2. 当时，作，解得综上，若是直角三角形，线段的长为或题型四、圆的综合（圆中函数关系建立）思路点拨：圆的综合在一模试卷中出现的不多，二模中是重点题型。与圆有关的问题主要分两类： 1.一是圆中函数关系式的建立，主要要利用垂径定理和勾股定理，有时还会结合三角 形的相似关系来建立关系式； 2.二是考察圆中的位置关系，包括点与圆、直线与圆和圆与圆的位置关系，
12、其中圆与 圆的相切关系考察频率较高，需重点掌握。解题方法主要是抓住代数上的等量关系再 结合一下图形即可求出，切忌和学生强调不要纠结在一定要画出图形才能解题。 例题1：（由垂径定理+锐角三角比得函数关系）如图，梯形ABCD中，AD/BC，CDBC，已知AB=5，BC=6，cosB=。点O为BC边上的动点，以O为圆心，BO为半径的O交边AB于点P。设，求与的函数关系式，并写出函数定义域例题2：（勾股定理得函数关系）在半径为4的O中，点C是以AB为直径的半圆的中点，ODAC，垂足为D，点E是射线AB上的任意一点，DF/AB，DF与CE相交于点F，设EF=，DF= （1）如图1，当点E在射线OB上时，
13、求关于的函数解析式，并写出函数定义域；（2）如图2，当点F在O上时，求线段DF的长例题3：（相似三角形）已知：O的直径AB=8，B与O相交于点C、D，O的直径CF与B相交于点E，设B的半径为，OE的长为。（1）如图，当点E在线段OC上时，求关于的函数解析式，并写出定义域；（2）当点E在直径CF上时，如果OE的长为3，求公共弦CD的长 1、如图，在中，是的中点，点在边上，将沿翻折，使得点落在点处，当时，=_.【答案】【解析】设AC的中点为H，则,DH=3，AH=CH=4.如图2，当时，因为DE平分AEA,得到DEH是等腰直角三角形.，CE=1，所以.此时A,B之间的水平距离，竖直距离都是1，所以
14、.如图3，,CE=7，此时A,B之间的水平距离，竖直距离都是7，所以.2、 如图，已知是边长为2的等边三角形，点在边上，将沿着直线翻折，点落在点处，如果，那么 。【答案】【解析】,垂足为3、在Rt中，D是斜边AB的中点（如图3），点M、N分别在边AC、BC上，将CMN沿直线MN翻折，使得点C的对应点E落在射线CD上，如果,那么度数为 .（用含的代数式表示）【答案】【解析】是斜边中线又4、一张直角三角形纸片，（如图），将它折叠使直角顶点与斜边的中点重合，那么折痕的长为_.【答案】13【解析】取AB的中点D，联结CD，过CD的中点M做直线EF交AC于点E，交BC于点F，有，且CM=6，利用锐角三角
15、比，有MF=4，ME=9，所以折痕的长为4+9=135、如图4，已知,将绕点顺时针旋转，使点落在边上的点处，点落在点处，联结，如果,那么的值是 。【答案】【解析】旋转易得 ,6、如图，在中，把绕着点旋转，使点与边上的点重合，点落在点，则点之间的距离为 .【答案】【解析】根据题目有，可得到：过点向做垂线段交于点，根据锐角三角比可求出可得：根据旋转可以得到，带入，求得：7、已知，的顶点D在BC边上，交边于点，交 边于点且交的延长线于点（点与点不重合），设，.（1） 求证：；（2） 设，求关于的函数关系式，并写出定义域；（3） 当是等腰三角形时，求的长.【答案】（1）根据一线三等角原理证明AA即可.
16、（2）（3）或【解析】（1）一线三等角模型可证（2） 过点作由相似可得即（3） 过点作交延长线于点可得当时，当时，当时，（舍去）综上所述，的长为或8、如图，已知四边形是矩形，点在射线上，点F在线段BD上，且.（1）求线段的长；（2）设，的面积为，求关于的函数解析式，并写出函数定义域；（3）当为等腰三角形时，求线段的长.【答案】（1）, （2） （3）BE=、24、20.【解析】(1)四边形为矩形 在直角三角形中， (2)四边形为矩形 在、中、 , (3)当为等腰三角形时，有下列三种情况： 当时， 当时, 当时， 综上所述：或或9、如图所示，矩形中，点是射线上的动点，点是射线上一点，且，射线与对角线交于点，与射线交于点.(1) 当点在线段上时，求证：；(2) 在（1）的条件下，联结，设，求关于的函数解析式，并写出的取值范围；(3) 当与相似时，求的长. 【答案】（1）略；（2）（3）的长为或.【解析】（1），（2） 由（1）得三角形相似，进而可得，如图1， 易得图2中的, （3） 如图3，当点在线段上时，与相似， ，只可能， ，解得，（舍） 如图4，当点在线段上时，与相似， , ,，解得，（舍） 综上，当与相似时，的长为或. 28 / 28
