1、2019-2020学年辽宁省沈阳市铁西区八年级（上）期末数学试卷一、选择题（下列各题的四个选项中，只有一个是正确的，请将正确答案写在答题卡上，每小题2分，共20分）1（2分）下列二次根式是最简二次根式的（）ABCD2（2分）下列选项中，哪个不可以得到l1l2？（）A12B23C35D3+41803（2分）满足下列条件时，ABC不是直角三角形的是（）A，BC4，AC5BAB：BC：AC3：4：5CA：B：C3：4：5DA2B2C4（2分）如图，A，B，C，D是数轴上的四个点，其中最适合表示无理数的点是（）A点AB点BC点CD点D5（2分）估计的值应在（）A5和6之间B6和7之间C7和8之间D8和
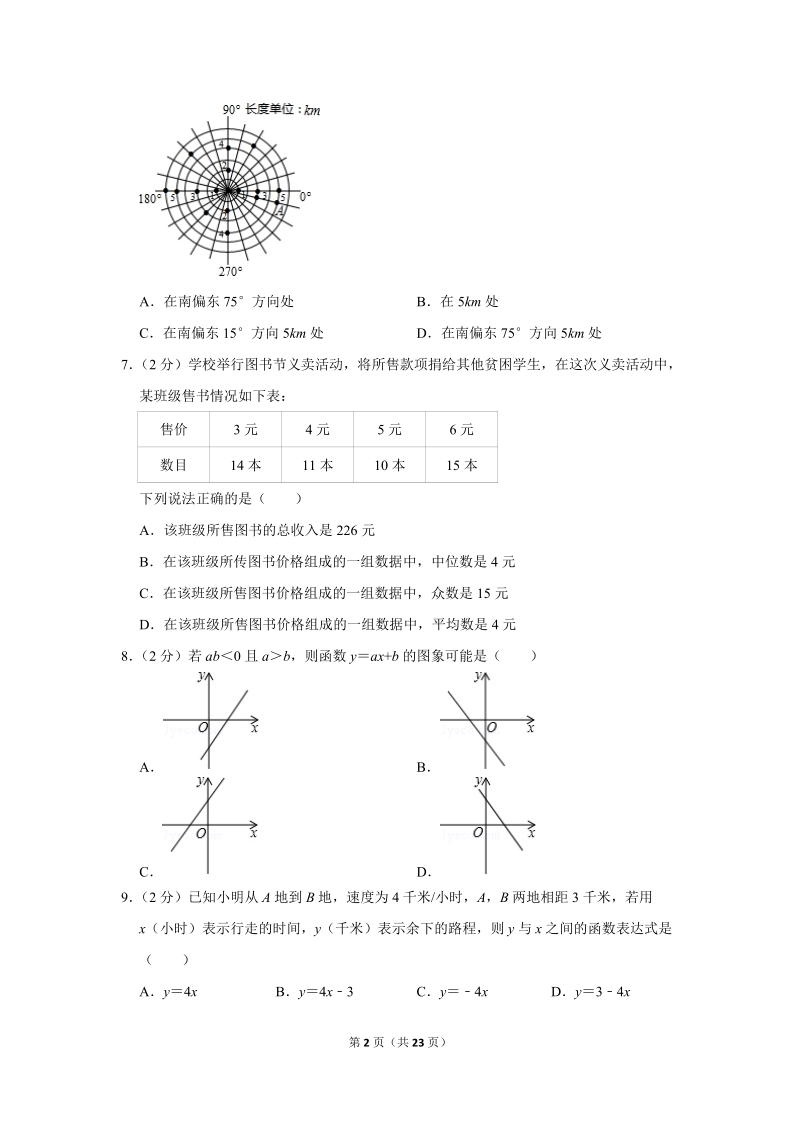
2、9之间6（2分）如图是雷达屏幕在一次探测中发现的多个目标，其中对目标A的位置表述正确的是（）A在南偏东75方向处B在5km处C在南偏东15方向5km处D在南偏东75方向5km处7（2分）学校举行图书节义卖活动，将所售款项捐给其他贫困学生，在这次义卖活动中，某班级售书情况如下表：售价3元4元5元6元数目14本11本10本15本下列说法正确的是（）A该班级所售图书的总收入是226元B在该班级所传图书价格组成的一组数据中，中位数是4元C在该班级所售图书价格组成的一组数据中，众数是15元D在该班级所售图书价格组成的一组数据中，平均数是4元8（2分）若ab0且ab，则函数yax+b的图象可能是（）ABC
3、D9（2分）已知小明从A地到B地，速度为4千米/小时，A，B两地相距3千米，若用x（小时）表示行走的时间，y（千米）表示余下的路程，则y与x之间的函数表达式是（）Ay4xBy4x3Cy4xDy34x10（2分）已知方程组，则2x+6y的值是（）A2B2C4D4二、填空题（每小题3分，共18分）11（3分）化简的结果是 12（3分）若正比例函数y2x的图象经过点A（a1，4），则a的值是 13（3分）如图，已知BE平分ABC，且BEDC，若ABC50，则C的度数是 14（3分）如图，等边OAB的边长为，则点B的坐标为 15（3分）若一组数据4，x，5，y，7，9的平均数为6，众数为5，则这组数据
4、的方差为 16（3分）如图，在ABC中，ACB90，以点B为圆心，BC为半径画弧，交线段AB于点D；以点A为圆心，AD长为半径画弧，交线段AC于点E设BCa，ACb，若ADEC，则a （用含b的式子表示）三、解答题（第17小题6分，第18、19小题各8分，共22分）17（6分）计算：（1）3+|1|+18（8分）解方程组：19（8分）如图，ABCD，点E为CD上点，射线EF经过点A，且ECEA，若CAE30，求BAF的度数四、（每题8分，共16分）20（8分）列二元一次方程组解决问题：某校八年级师生共466人准备参加社会实践活动，现已预备了A，B两种型号的客车共10辆，每辆A种型号客车坐师生4
5、9人，每辆B种型号客车坐师生37人，10辆客车刚好坐满，求A，B两种型号客车各多少辆？21（8分）如图，在平面直角坐标系中，已知四边形OABC的顶点A（1，2），B（3，3）（1）画出四边形OABC关于y轴的对称图形OABC；（2）请直接写出点C关于x轴的对称点C的坐标： 五、（本题10分）22（10分）为了了解居民的环保意识，社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动，并用得到的数据绘制了如图条形统计图（得分为整数，满分为10分，最低分为6分）请根据图中信息，解答下列问题：（1）本次调查一共抽取了 名居民；（2）求本次调查获取的样本数据的平均
6、数、众数和中位数；（3）社区决定对该小区500名居民开展这项有奖问答活动，得10分者设为“一等奖”，请你根据调查结果，帮社区工作人员估计需准备多少份“一等奖”奖品？六、（本题10分）23（10分）为加快“智慧校园”建设，某市准备为试点学校采购一批A，B两种型号的一体机，经过市场调查发现，每套B型一体机的价格比每套A型一体机的价格多0.6万元，且用960万元恰好能购买500套A型一体机和200套B型一体机（1）列二元一次方程组解决问题：求每套A型和B型一体机的价格各是多少万元？（2）由于需要，决定再次采购A型和B型一体机共1100套，此时每套A型体机的价格比原来上涨25%，每套B型一体机的价格不
7、变设再次采购A型一体机m（m600）套，那么该市至少还需要投入多少万元？七、（本题10分）24（12分）在RtABC中，BAC90，ABAC2，ADBC于点D（1）如图1所示，点M，N分别在线段AD，AB上，且BMN90，当AMN30时，求线段AM的长；（2）如图2，点M在线段AD的延长线上，点N在线段AC上，（1）中其他条件不变线段AM的长为 ；求线段AN的长八、（本题12分）25（12分）如图，在平面直角坐标系中，直线yx+2与x轴交于点A，点B（5，n）在直线yx+2上，点C是线段AB上的一个动点，过点C作CPx轴交直线点P，设点C的横坐标为m（1）n的值为 ；（2）用含有m的式子表示线
8、段CP的长；（3）若APB的面积为S，求S与m之间的函数表达式，并求出当S最大时点P的坐标；（4）在（3）的条件下，把直线AB沿着y轴向下平移，交y轴于点M，交线段BP于点N，若点D的坐标为，在平移的过程中，当DMN90时，请直接写出点N的坐标2019-2020学年辽宁省沈阳市铁西区八年级（上）期末数学试卷参考答案与试题解析一、选择题（下列各题的四个选项中，只有一个是正确的，请将正确答案写在答题卡上，每小题2分，共20分）1（2分）下列二次根式是最简二次根式的（）ABCD【分析】根据最简二次根式的定义逐个判断即可【解答】解：A、，不是最简二次根式，故本选项不符合题意；B、，不是最简二次根式，故
9、本选项不符合题意；C、2，不是最简二次根式，故本选项不符合题意；D、是最简二次根式，故本选项符合题意；故选：D【点评】本题考查了最简二次根式的定义，能熟记最简二次根式的定义的内容是解此题的关键2（2分）下列选项中，哪个不可以得到l1l2？（）A12B23C35D3+4180【分析】分别根据平行线的判定定理对各选项进行逐一判断即可【解答】解：A、12，l1l2，故本选项错误；B、23，l1l2，故本选项错误；C、35不能判定l1l2，故本选项正确；D、3+4180，l1l2，故本选项错误故选：C【点评】本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键3（2分）满足下列条件时，ABC
10、不是直角三角形的是（）A，BC4，AC5BAB：BC：AC3：4：5CA：B：C3：4：5DA2B2C【分析】依据勾股定理的逆定理，三角形内角和定理以及直角三角形的性质，即可得到结论【解答】解：A、52+4225+1641（）2，ABC是直角三角形，错误；B、（3x）2+（4x）29x2+16x2252（5x）2，ABC是直角三角形，错误；C、A：B：C3：4：5，C1807590，ABC不是直角三角形，正确；D、A2B2C，A90，BC45，ABC是直角三角形，错误；故选：C【点评】本题考查了直角三角形的判定及勾股定理的逆定理，掌握直角三角形的判定及勾股定理的逆定理是解题的关键4（2分）如图
11、，A，B，C，D是数轴上的四个点，其中最适合表示无理数的点是（）A点AB点BC点CD点D【分析】能够估算无理数的范围，结合数轴找到点即可【解答】解：因为无理数大于3，在数轴上表示大于3的点为点D；故选：D【点评】本题考查无理数和数轴的关系；能够准确估算无理数的范围是解题的关键5（2分）估计的值应在（）A5和6之间B6和7之间C7和8之间D8和9之间【分析】化简原式等于3，因为3，所以，即可求解；【解答】解：+23，3，67，故选：B【点评】本题考查无理数的大小；能够将给定的无理数锁定在相邻的两个整数之间是解题的关键6（2分）如图是雷达屏幕在一次探测中发现的多个目标，其中对目标A的位置表述正确的
12、是（）A在南偏东75方向处B在5km处C在南偏东15方向5km处D在南偏东75方向5km处【分析】根据方向角的定义即可得到结论【解答】解：由图可得，目标A在南偏东75方向5km处，故选：D【点评】此题主要考查了方向角，正确理解方向角的意义是解题关键7（2分）学校举行图书节义卖活动，将所售款项捐给其他贫困学生，在这次义卖活动中，某班级售书情况如下表：售价3元4元5元6元数目14本11本10本15本下列说法正确的是（）A该班级所售图书的总收入是226元B在该班级所传图书价格组成的一组数据中，中位数是4元C在该班级所售图书价格组成的一组数据中，众数是15元D在该班级所售图书价格组成的一组数据中，平均
13、数是4元【分析】根据平均数、众数和中位数的概念逐一判断即可得【解答】解：A该班级所售图书的总收入是314+411+510+615226（元），此选项正确；B在该班级所传图书价格组成的一组数据中，中位数是4.5（元），此选项错误；C在该班级所售图书价格组成的一组数据中，众数是6元，此选项错误；D在该班级所售图书价格组成的一组数据中，平均数是4.52（元），此选项错误；故选：A【点评】本题主要考查中位数、众数和平均数，解题的关键是掌握平均数、众数和中位数的概念8（2分）若ab0且ab，则函数yax+b的图象可能是（）ABCD【分析】利用ab0，且ab得到a0，b0，然后根据一次函数图象与系数的关系
14、进行判断【解答】解：ab0，且ab，a0，b0，函数yax+b的图象经过第一、三、四象限故选：A【点评】本题考查了一次函数图象与系数的关系：一次函数ykx+b（k、b为常数，k0）是一条直线，当k0，图象经过第一、三象限，y随x的增大而增大；当k0，图象经过第二、四象限，y随x的增大而减小；图象与y轴的交点坐标为（0，b）9（2分）已知小明从A地到B地，速度为4千米/小时，A，B两地相距3千米，若用x（小时）表示行走的时间，y（千米）表示余下的路程，则y与x之间的函数表达式是（）Ay4xBy4x3Cy4xDy34x【分析】直接利用总路程行驶的路程余下的路程，进而得出答案【解答】解：用x（小时）
15、表示行走的时间，y（千米）表示余下的路程，则y与x之间的函数表达式是：y34x故选：D【点评】此题主要考查了根据实际问题列一次函数解析式，正确理解题意表示出行驶路程是解题关键10（2分）已知方程组，则2x+6y的值是（）A2B2C4D4【分析】两式相减，得x+3y2，所以2（x+3y）4，即2x+6y4【解答】解：两式相减，得x+3y2，2（x+3y）4，即2x+6y4，故选：C【点评】本题考查了二元一次方程组，对原方程组进行变形是解题的关键二、填空题（每小题3分，共18分）11（3分）化简的结果是4【分析】直接利用二次根式的性质化简得出答案【解答】解：4故答案为：4【点评】此题主要考查了二次
16、根式的化简，正确掌握二次根式的性质是解题关键12（3分）若正比例函数y2x的图象经过点A（a1，4），则a的值是1【分析】由正比例函数图象过点O，可知点O的坐标满足正比例函数的关系式，由此可得出关于a的一元一次方程，解方程即可得出结论【解答】解：正比例函数y2x的图象经过点O（a1，4），42（a1），解得：a1故答案为：1【点评】本题考查了一次函数图象上点的坐标特征，解题的关键是将点O的坐标代入正比例函数关系得出关于a的一元一次方程本题属于基础题，难度不大，解决该题型题目时，将点的坐标代入函数解析式中找出方程是关键13（3分）如图，已知BE平分ABC，且BEDC，若ABC50，则C的度数是2
17、5【分析】直接利用角平分线的定义结合平行线的性质分析得出答案【解答】解：BE平分ABC，ABC50，ABEEBC25，BEDC，CEBC25故答案为：25【点评】此题主要考查了平行线的性质，得出EBC25是解题关键14（3分）如图，等边OAB的边长为，则点B的坐标为（，3）【分析】如图，作BHOA于H解直角三角形求出OH，BH即可【解答】解：如图，作BHOA于HOAB是等边三角形，BHOA，OHAH，BOH60，BHOHtan603，B（，3），故答案为（，3）【点评】本题考查坐标与图形的性质，等边三角形的性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直径三角形解决问题15（3
18、分）若一组数据4，x，5，y，7，9的平均数为6，众数为5，则这组数据的方差为【分析】根据众数的定义先判断出x，y中至少有一个是5，再根据平均数的计算公式求出x+y11，然后代入方差公式即可得出答案【解答】解：一组数据4，x，5，y，7，9的平均数为6，众数为5，x，y中至少有一个是5，一组数据4，x，5，y，7，9的平均数为6，（4+x+5+y+7+9）6，x+y11，x，y中一个是5，另一个是6，这组数据的方差为（46）2+2（56）2+（66）2+（76）2+（96）2；故答案为：【点评】此题考查了众数、平均数和方差，一般地设n个数据，x1，x2，xn的平均数为，则方差S2（x1）2+（
19、x2）2+（xn）2；解答本题的关键是掌握各个知识点的概念16（3分）如图，在ABC中，ACB90，以点B为圆心，BC为半径画弧，交线段AB于点D；以点A为圆心，AD长为半径画弧，交线段AC于点E设BCa，ACb，若ADEC，则a（用含b的式子表示）【分析】利用勾股定理构建方程即可解决问题【解答】解：由作图可知：ADAE，BCBDa，ADEC，AEECADb，C90，AB2AC2+BC2，（b+a）2a2+b2，整理得：b2ab，b0，ab，故答案为b【点评】本题考查勾股定理，解题的关键是学会利用勾股定理构建关系式解决问题三、解答题（第17小题6分，第18、19小题各8分，共22分）17（6分
20、）计算：（1）3+|1|+【分析】原式利用乘方的意义，绝对值的代数意义，以及立方根定义计算即可求出值【解答】解：原式1+1+2【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键18（8分）解方程组：【分析】+得出4x8，求出x，再把x2代入求出y即可【解答】解：，+得：4x8，解得：x2，将x2代入得：2+2y0，解得：y1，所以原方程组的解为【点评】本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键19（8分）如图，ABCD，点E为CD上点，射线EF经过点A，且ECEA，若CAE30，求BAF的度数【分析】先根据ECEACAE30得出C30，再由三角形外
21、角的性质得出AED的度数，利用平行线的性质即可得出结论【解答】解：ECEA，CAE30，CCAE30，DEA是ACE的外角，AEDC+CAE30+3060，ABCD，BAFAED60【点评】本题考查的是平行线的性质，熟知两直线平行，同位角相等是解答此题的关键四、（每题8分，共16分）20（8分）列二元一次方程组解决问题：某校八年级师生共466人准备参加社会实践活动，现已预备了A，B两种型号的客车共10辆，每辆A种型号客车坐师生49人，每辆B种型号客车坐师生37人，10辆客车刚好坐满，求A，B两种型号客车各多少辆？【分析】设A种型号客车x辆，B种型号客车y辆，根据A，B两种型号的客车共10辆，每
22、种型号车的辆数乘以每辆乘坐的人数等于总人数，列出方程组即可解答【解答】解：设A种型号客车x辆，B种型号客车y辆，依题意，得解得答：A种型号客车8辆，B种型号客车2辆【点评】本题考查了二元一次方程组的应用，解决本题的关键是根据题意找到等量关系21（8分）如图，在平面直角坐标系中，已知四边形OABC的顶点A（1，2），B（3，3）（1）画出四边形OABC关于y轴的对称图形OABC；（2）请直接写出点C关于x轴的对称点C的坐标：（2，1）【分析】（1）分别作出点A、B、C关于y轴的对称图形，再与点O首尾顺次连接即可得；（2）根据平面直角坐标系中点的坐标对称规律求解可得【解答】解：（1）如图所示，四边
23、形OABC即为所求（2）如图，点C即为所求，其坐标为（2，1）故答案为：（2，1）【点评】本题主要考查作图轴对称变换，解题的关键是掌握轴对称变换的定义和性质五、（本题10分）22（10分）为了了解居民的环保意识，社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动，并用得到的数据绘制了如图条形统计图（得分为整数，满分为10分，最低分为6分）请根据图中信息，解答下列问题：（1）本次调查一共抽取了50名居民；（2）求本次调查获取的样本数据的平均数、众数和中位数；（3）社区决定对该小区500名居民开展这项有奖问答活动，得10分者设为“一等奖”，请你根据调查结果
24、，帮社区工作人员估计需准备多少份“一等奖”奖品？【分析】（1）根据总数个体数量之和计算即可；（2）根据平均数、总数、中位数的定义计算即可；（3）利用样本估计总体的思想解决问题即可；【解答】解：（1）共抽取：4+10+15+11+1050（人），故答案为50；（2）平均数（46+107+158+119+1010）8.26；众数：得到8分的人最多，故众数为8中位数：由小到大排列，知第25，26平均分为8分，故中位数为8分；（3）得到10分占105020%，故500人时，需要一等奖奖品50020%100（份）【点评】本题考查的是条形统计图综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题
25、的关键条形统计图能清楚地表示出每个项目的数据；六、（本题10分）23（10分）为加快“智慧校园”建设，某市准备为试点学校采购一批A，B两种型号的一体机，经过市场调查发现，每套B型一体机的价格比每套A型一体机的价格多0.6万元，且用960万元恰好能购买500套A型一体机和200套B型一体机（1）列二元一次方程组解决问题：求每套A型和B型一体机的价格各是多少万元？（2）由于需要，决定再次采购A型和B型一体机共1100套，此时每套A型体机的价格比原来上涨25%，每套B型一体机的价格不变设再次采购A型一体机m（m600）套，那么该市至少还需要投入多少万元？【分析】（1）根据今年每套B型一体机的价格比每
26、套A型一体机的价格多0.6万元，且用960万元恰好能购买500套A型一体机和200套B型一体机，分别得出方程求出答案；（2）设该市还需要投入W万元，由题意得W1.2（1+25%）m+1.8（1100m）0.3m+1980，由一次函数的性质即可得出答案【解答】解：（1）设每套A型一体机的价格为x万元，每套B型一体机的价格为y万元由题意可得：，解得：，答：每套A型一体机的价格是1.2万元，B型一体机的价格是1.8万元；（2）设该市还需要投入W万元，由题意得：W1.2（1+25%）m+1.8（1100m）0.3m+1980，0.30，W随m的增大而减小m600，当m600时，W有最小值，W最小0.3
27、600+19801800，答：该市至少还需要投入1800万元【点评】此题主要考查了二元一次方程组的应用以及一次函数的应用，正确找出等量关系是解题关键七、（本题10分）24（12分）在RtABC中，BAC90，ABAC2，ADBC于点D（1）如图1所示，点M，N分别在线段AD，AB上，且BMN90，当AMN30时，求线段AM的长；（2）如图2，点M在线段AD的延长线上，点N在线段AC上，（1）中其他条件不变线段AM的长为；求线段AN的长【分析】（1）根据等腰三角形的性质、直角三角形的性质得到ADBDDC，求出MBD30，根据勾股定理计算即可；（2）根据等腰三角形的性质、直角三角形的性质得到ADB
28、DDC，求出MBD30，根据勾股定理计算即可；过点M作MEBC交AB的延长线于点E，根据全等三角形的判定和性质以及勾股定理即可得到结论【解答】解：（1）BAC90，ABAC，ADBC，ABCACB45，BADCAD45，ABCBADCADACB45，在RtABC中，BAC90，ABAC2，根据勾股定理，AMN30，BMN90，BMD180903060，MBD30，BM2DM，在RtBDM中，BDM90，由勾股定理得，BM2DM2BD2，即，解得，；（2）BAC90，ABAC，ADBC，ABCACB45，BADCAD45，ABCBADCADACB45，在RtABC中，BAC90，ABAC2，根据
29、勾股定理，AMN30，BMN90，BMD180903060，MBD30，BM2DM，在RtBDM中，BDM90，由勾股定理得，BM2DM2BD2，即，解得，AMAD+DM；故答案为：；过点M作MEBC交AB的延长线于点E，ADBC，ADB90，AMEADB90，E45BAD，MEMA，ECAD45，AMN30，BMN90，AME90，BME30AMN，BMENMA（ASA），BEAN，在RtAME中，AME90，由，根据勾股定理，ANBEAEAB【点评】本题考查的是等腰直角三角形的性质、全等三角形的判定和性质、直角三角形的性质，掌握全等三角形的判定定理和性质定理是解题的关键八、（本题12分）2
30、5（12分）如图，在平面直角坐标系中，直线yx+2与x轴交于点A，点B（5，n）在直线yx+2上，点C是线段AB上的一个动点，过点C作CPx轴交直线点P，设点C的横坐标为m（1）n的值为7；（2）用含有m的式子表示线段CP的长；（3）若APB的面积为S，求S与m之间的函数表达式，并求出当S最大时点P的坐标；（4）在（3）的条件下，把直线AB沿着y轴向下平移，交y轴于点M，交线段BP于点N，若点D的坐标为，在平移的过程中，当DMN90时，请直接写出点N的坐标【分析】（1）点B（5，n）在直线yx+2上，则n7，即可求解；（2）点C的横坐标为m，点C（m，m+2），CPx轴交直线于点P，则点，；（
31、3）SAPC的面积+BPC的面积，即可求解；（4）直线AB的倾斜角为45，则GMN45，DMN90，则GMNMDH45，故MHDH，即2m（）2，解得：m，即可求解【解答】解：（1）点B（5，n）在直线yx+2上，则n7，故答案为：7；（2）点C的横坐标为m，点C（m，m+2），CPx轴交直线于点P，点，；（3）直线yx+2与x轴交于点A，点A（2，0），SAPC的面积+BPC的面积，S随m的增大而增大，点C是线段AB上的一个动点，当点C与点B重合时，m有最大值，即m5时，S有最大值当m5时，点；（4）过点N作NGy轴于点G，过点D作DHy轴于点H，设直线向下平移m个单位，则平移后直线的表达式为：xx+2m，故点M（0，2m），点N（5，7m），直线AB的倾斜角为45，则GMN45，DMN90，则GMNMDH45，故MHDH，即2m（）2，解得：m，故：点【点评】本题考查的是一次函数综合运用，涉及到一次函数的性质、三角形相似、图形的平移、面积的计算等，综合性强，难度适中
