1、2019-2020学年辽宁省沈阳市大东区八年级（上）期末数学试卷一、选择题（下列各题的备选答案中，只有一个答案是正确的每小题2分，共20分）1（2分）下列各组数中，能构成直角三角形的是（）A4，5，6B1，1，C6，8，11D5，12，232（2分）下列各数中，是无理数的是（）A3.1415BCD3（2分）下列各点中，在第三象限的点是（）A（1，4）B（1，4）C（1，4）D（1，4）4（2分）下列各式中，无论x为任何数都没有意义的是（）ABCD5（2分）某班40名同学一周参加体育锻炼时间统计如表所示：人数（人）317137时间（小时）78910那么该班40名同学一周参加体育锻炼时间的众数、中
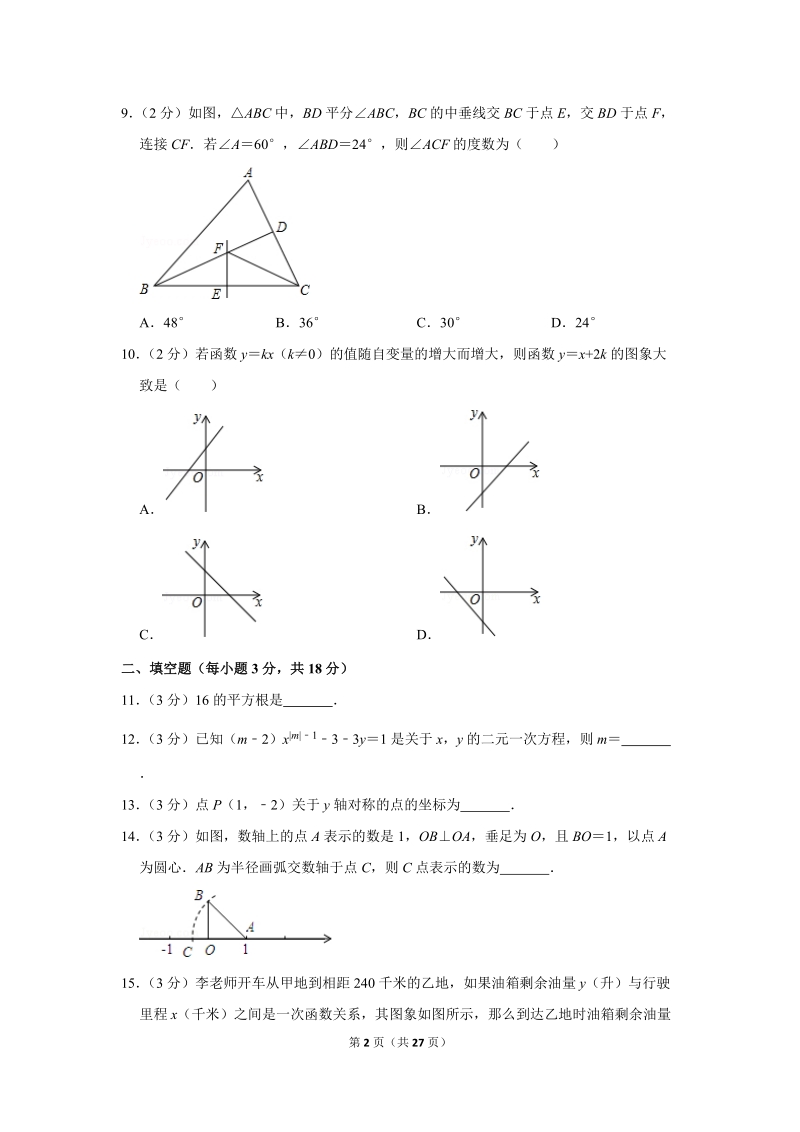
2、位数分别是（）A17，8.5B17，9C8，9D8，8.56（2分）已知a，b满足方程组，则a+b的值为（）A4B4C2D27（2分）下列命题中的假命题是（）A两直线平行，内错角相等B同位角相等，两直线平行C两直线平行，同旁内角相等D平行于同一条直线的两直线平行8（2分）如图所示是一条街道的路线图，若ABCD，且ABC130，那么当CDE等于（）时，BCDEA40B50C70D1309（2分）如图，ABC中，BD平分ABC，BC的中垂线交BC于点E，交BD于点F，连接CF若A60，ABD24，则ACF的度数为（）A48B36C30D2410（2分）若函数ykx（k0）的值随自变量的增大而增大，
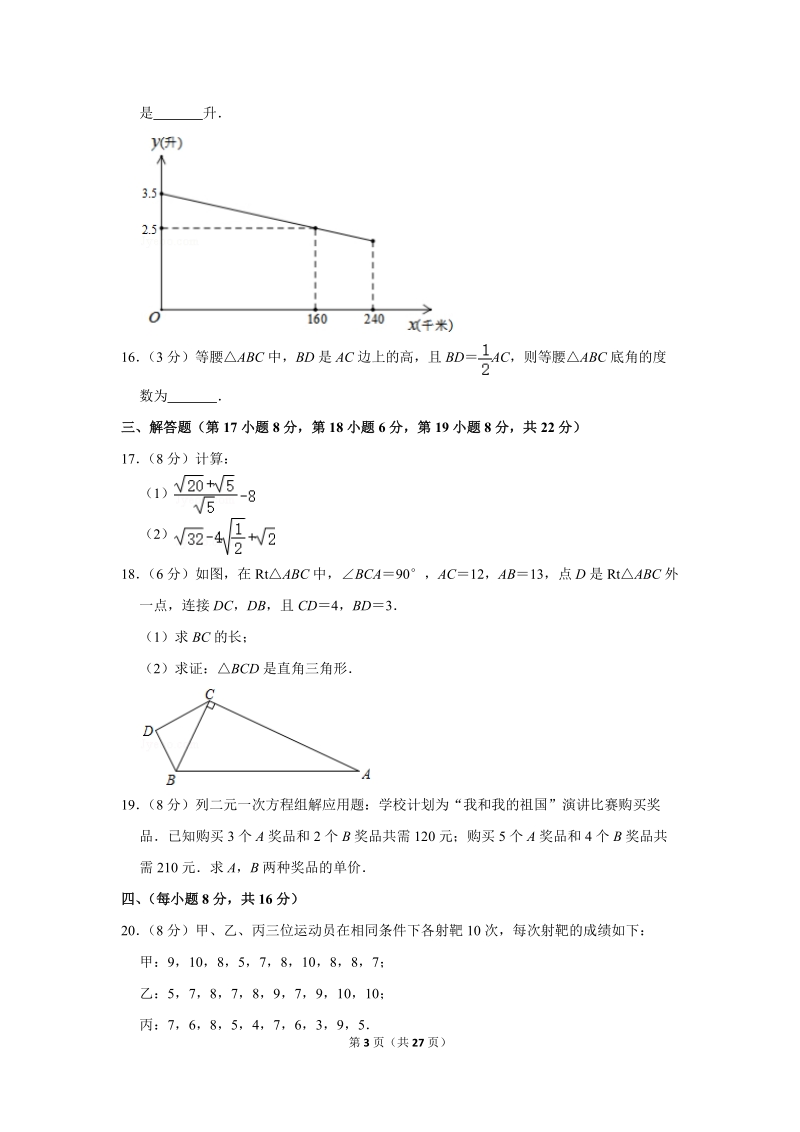
3、则函数yx+2k的图象大致是（）ABCD二、填空题（每小题3分，共18分）11（3分）16的平方根是 12（3分）已知（m2）x|m|133y1是关于x，y的二元一次方程，则m 13（3分）点P（1，2）关于y轴对称的点的坐标为 14（3分）如图，数轴上的点A表示的数是1，OBOA，垂足为O，且BO1，以点A为圆心AB为半径画弧交数轴于点C，则C点表示的数为 15（3分）李老师开车从甲地到相距240千米的乙地，如果油箱剩余油量y（升）与行驶里程x（千米）之间是一次函数关系，其图象如图所示，那么到达乙地时油箱剩余油量是 升16（3分）等腰ABC中，BD是AC边上的高，且BDAC，则等腰ABC底角
4、的度数为 三、解答题（第17小题8分，第18小题6分，第19小题8分，共22分）17（8分）计算：（1）（2）18（6分）如图，在RtABC中，BCA90，AC12，AB13，点D是RtABC外一点，连接DC，DB，且CD4，BD3（1）求BC的长；（2）求证：BCD是直角三角形19（8分）列二元一次方程组解应用题：学校计划为“我和我的祖国”演讲比赛购买奖品已知购买3个A奖品和2个B奖品共需120元；购买5个A奖品和4个B奖品共需210元求A，B两种奖品的单价四、（每小题8分，共16分）20（8分）甲、乙、丙三位运动员在相同条件下各射靶10次，每次射靶的成绩如下：甲：9，10，8，5，7，8，
5、10，8，8，7；乙：5，7，8，7，8，9，7，9，10，10；丙：7，6，8，5，4，7，6，3，9，5（1）根据以上数据完成下表：平均数中位数方差甲88 乙882.2丙6 3（2）依据表中数据分析，哪位运动员的成绩最稳定，并简要说明理由21（8分）如图，已知：ABC，A52，ACB56，点D，E分别在AB，AC上，连接DE，且ADE72，F是AD上一点，FE的延长线交BC的延长线于点G（1）求证：DEBC；（2）求证：EGHADE五、（本题10分）22（10分）如图，在ABC中，C90，A30，AB的垂直平分线交AB，AC于点D，E（1）求证：AE2CE；（2）当DE1时，求ABC的面积
6、六、（本题10分）23（10分）已知：如图1，在平面直角坐标系中，长方形OABC的顶点B的坐标是（6，4）（1）直接写出A点坐标（ ， ），C点坐标（ ， ）；（2）如图2，D为OC中点连接BD，AD，如果在第二象限内有一点P（m，1），且四边形OADP的面积是ABC面积的2倍，求满足条件的点P的坐标；（3）如图3，动点M从点C出发，以每钞1个单位的速度沿线段CB运动，同时动点N从点A出发以每秒2个单位的速度沿线段AO运动，当N到达O点时，M，N同时停止运动，运动时间是t秒（t0），在M，N运动过程中当MN5时，直接写出时间t的值七、（本题12分）24（12分）如图，在平面立角坐标系xOy中，
7、直线AB与x轴，y轴分别交于点A（3，0）、点B（0，4），点C在y轴的负半轴上，若将CAB沿直线AC折叠，点B恰好落在x轴正半轴上的点D处（1）直接写出AB的长 ；（2）求直线AB的函数表达式；（3）求点D和点C的坐标；（4）y轴上是否存在一点P，使得SPABSOCD？若存在，直接写出点P的坐标；若不存在，请说明理由八、（本题12分）25（12分）如图1，已知RtABC，ACB90，BAC30，斜边AB4，ED为AB垂直平分线，且DE2，连接DB，DA（1）直接写出BC ，AC ；（2）求证：ABD是等边三角形；（3）如图2，连接CD，作BFCD，垂足为点F，直接写出BF的长；（4）P是直线
8、AC上的一点，且CPAC，连接PE，直接写出PE的长2019-2020学年辽宁省沈阳市大东区八年级（上）期末数学试卷参考答案与试题解析一、选择题（下列各题的备选答案中，只有一个答案是正确的每小题2分，共20分）1（2分）下列各组数中，能构成直角三角形的是（）A4，5，6B1，1，C6，8，11D5，12，23【分析】根据勾股定理逆定理：a2+b2c2，将各个选项逐一代数计算即可得出答案【解答】解：A、42+5262，不能构成直角三角形，故A错误；B、12+12，能构成直角三角形，故B正确；C、62+82112，不能构成直角三角形，故C错误；D、52+122232，不能构成直角三角形，故D错误故
9、选：B【点评】此题主要考查学生对勾股定理的逆定理的理解和掌握，要求学生熟练掌握这个逆定理2（2分）下列各数中，是无理数的是（）A3.1415BCD【分析】根据无理数的定义：无限不循环小数进行判断，2是有理数；【解答】解：2是有理数，是无理数，故选：D【点评】本题考查无理数的定义；能够准确辨识无理数是解题的关键3（2分）下列各点中，在第三象限的点是（）A（1，4）B（1，4）C（1，4）D（1，4）【分析】根据平面直角坐标系中各个象限的点的坐标的符号特点即可解答【解答】解：第三象限的点的坐标特点是横纵坐标均小于0，结合四个选项中只有A（1，4 ）符合条件故选：A【点评】本题主要考查了平面直角坐标
10、系中各个象限的点的坐标的符号特点，四个象限的符号特点分别是：第一象限（+，+）；第二象限（，+）；第三象限（，）；第四象限（+，）4（2分）下列各式中，无论x为任何数都没有意义的是（）ABCD【分析】根据二次根式中的被开方数是非负数，判断出无论x为任何数都没有意义的是哪个式子即可【解答】解：x0时，6x0，A不符合题意；x0时，199x30，B不符合题意；无论x为任何数，0.01x210，C符合题意；无论x为任何数，都有意义，D不符合题意故选：C【点评】此题主要考查了二次根式有意义的条件和应用，要熟练掌握，解答此题的关键是要明确：二次根式中的被开方数是非负数5（2分）某班40名同学一周参加体育
11、锻炼时间统计如表所示：人数（人）317137时间（小时）78910那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是（）A17，8.5B17，9C8，9D8，8.5【分析】根据中位数、众数的概念分别求得这组数据的中位数、众数【解答】解：众数是一组数据中出现次数最多的数，即8；由统计表可知，处于20，21两个数的平均数就是中位数，这组数据的中位数为8.5；故选：D【点评】本题考查了中位数、众数的概念本题为统计题，考查众数与中位数的意义，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数6（2分）已知a，b满足方程组，则a+b的
12、值为（）A4B4C2D2【分析】求出方程组的解得到a与b的值，即可确定出a+b的值【解答】解：法1：，+5得：16a32，即a2，把a2代入得：b2，则a+b4，法2：+得：4a+4b16，则a+b4，故选：B【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法7（2分）下列命题中的假命题是（）A两直线平行，内错角相等B同位角相等，两直线平行C两直线平行，同旁内角相等D平行于同一条直线的两直线平行【分析】直接利用平行线的性质与判定分别判断得出答案【解答】解：A、两直线平行，内错角相等，是真命题，不合题意；B、同位角相等，两直线平行，是真命题，不合题意；C、
13、两直线平行，同旁内角互补，故原命题是假命题，符合题意；D、平行于同一条直线的两直线平行，是真命题，不合题意；故选：C【点评】此题主要考查了命题与定理，正确掌握平行线的性质与判定是解题关键8（2分）如图所示是一条街道的路线图，若ABCD，且ABC130，那么当CDE等于（）时，BCDEA40B50C70D130【分析】首先利用平行线的性质定理得到BCD130，然后利用同旁内角互补两直线平行得到CDE的度数即可【解答】解：ABCD，且ABC130，BCDABC130，当BCD+CDE180时BCDE，CDE180BCD18013050，故选：B【点评】本题考查了平行线的判定与性质，注意平行线的性质
14、与判定方法的区别与联系9（2分）如图，ABC中，BD平分ABC，BC的中垂线交BC于点E，交BD于点F，连接CF若A60，ABD24，则ACF的度数为（）A48B36C30D24【分析】根据角平分线的性质可得DBCABD24，然后再计算出ACB的度数，再根据线段垂直平分线的性质可得BFCF，进而可得FCB24，然后可算出ACF的度数【解答】解：BD平分ABC，DBCABD24，A60，ACB1806024272，BC的中垂线交BC于点E，BFCF，FCB24，ACF722448，故选：A【点评】此题主要考查了线段垂直平分线的性质，以及三角形内角和定理，关键是掌握线段垂直平分线上任意一点，到线段
15、两端点的距离相等10（2分）若函数ykx（k0）的值随自变量的增大而增大，则函数yx+2k的图象大致是（）ABCD【分析】先根据正比例函数ykx（k是常数，k0）的函数值y随x的增大而增大判断出k的符号，再根据一次函数的图象与系数的关系即可得出结论【解答】解：正比例函数ykx（k是常数，k0）的函数值y随x的增大而增大，k0，一次函数yx+2k，k10，b2k0，此函数的图象经过一、二、三象限故选：A【点评】本题主要考查一次函数的图象与系数的关系，掌握ykx+b（k0）的图象与系数的关系是解题的关键当k0，b0时，图象过一、二、三象限，当k0，b0时，图象过一、三、四象限，当k0，b0时，图象
16、过一、二、四象限，当k0，b0时，图象过二、三、四象限二、填空题（每小题3分，共18分）11（3分）16的平方根是4【分析】根据平方根的定义，求数a的平方根，也就是求一个数x，使得x2a，则x就是a的平方根，由此即可解决问题【解答】解：（4）216，16的平方根是4故答案为：4【点评】本题考查了平方根的定义注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根12（3分）已知（m2）x|m|133y1是关于x，y的二元一次方程，则m2【分析】根据（m2）x|m|133y1是关于x，y的二元一次方程，可得：，据此求出m的值是多少即可【解答】解：（m2）x|m|133y1是关于x
17、，y的二元一次方程，由，可得：m2，由，可得：m2，m2故答案为：2【点评】此题主要考查了二元一次方程的定义，要熟练掌握，解答此题的关键是要明确：二元一次方程需满足三个条件：首先是整式方程方程中共含有两个未知数所有未知项的次数都是一次13（3分）点P（1，2）关于y轴对称的点的坐标为（1，2）【分析】根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”解答即可【解答】解：点P（1，2）关于y轴对称的点的坐标为（1，2）故答案为：（1，2）【点评】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴
18、对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数14（3分）如图，数轴上的点A表示的数是1，OBOA，垂足为O，且BO1，以点A为圆心AB为半径画弧交数轴于点C，则C点表示的数为1【分析】利用勾股定理求出AB的长，可得ABAC，推出OC1即可解决问题【解答】解：在RtAOB中，AB，ABAC，OCACOA1，点C表示的数为1故答案为：1【点评】本题考查实数与数轴、勾股定理等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考基础题15（3分）李老师开车从甲地到相距240千米的乙地，如果油箱剩余油量y（升）与行驶里程x（千米）之间是一次函数关系
19、，其图象如图所示，那么到达乙地时油箱剩余油量是2升【分析】先运用待定系数法求出y与x之间的函数关系式，然后把x240时代入解析式就可以求出y的值，从而得出剩余的油量【解答】解：设y与x之间的函数关系式为ykx+b，由函数图象，得，解得：，则yx+35当x240时，y240+3.52（升）故答案为：2【点评】本题考查了运用待定系数法求一次函数的运用，根据自变量求函数值的运用，解答时理解函数图象的含义求出一次函数的解析式是关键16（3分）等腰ABC中，BD是AC边上的高，且BDAC，则等腰ABC底角的度数为15或45或75【分析】分点B是顶角顶点、点B是底角顶点、BD在ABC外部和BD在ABC内部
20、三种情况，根据等腰三角形的性质、直角三角形的性质计算【解答】解：如图1，当点B是顶角顶点时，ABBC，BDAC，ADCD，BDAC，BDADCD，在RtABD中，AABD（18090）45；如图2，当点B是底角顶点，且BD在ABC外部时，BDAC，ACBC，BDBC，BCD30，ABCBAC3015；如图3，当点B是底角顶点，且BD在ABC内部时，BDAC，ACBC，BDBC，C30，ABCBAC（18030）75；故答案为：15或45或75【点评】本题考查的是直角三角形的性质、等腰三角形的性质，掌握在直角三角形中，30角所对的直角边等于斜边的一半是解题的关键三、解答题（第17小题8分，第18
21、小题6分，第19小题8分，共22分）17（8分）计算：（1）（2）【分析】（1）首先求出分数的值是多少，然后用它减去8，求出算式的值是多少即可（2）首先计算开方，然后计算乘法，最后从左向右依次计算，求出算式的值是多少即可【解答】解：（1）2+185；（2）42+3【点评】此题主要考查了二次根式的混合运算，要熟练掌握，解答此题的关键是要明确：与有理数的混合运算一致，运算顺序先乘方再乘除，最后加减，有括号的先算括号里面的在运算中每个根式可以看做是一个“单项式”，多个不同类的二次根式的和可以看作“多项式”18（6分）如图，在RtABC中，BCA90，AC12，AB13，点D是RtABC外一点，连接D
22、C，DB，且CD4，BD3（1）求BC的长；（2）求证：BCD是直角三角形【分析】（1）在RtABC中，根据勾股定理即可求得BC的长；（2）利用勾股定理逆定理即可证明BCD是直角三角形【解答】（1）解：RtABC中，BCA90，AC12，AB13，BC5；（2）证明：在BCD中，CD4，BD3，BC5，CD2+BD2BC2，BCD是直角三角形【点评】本题考查了勾股定理及其逆定理勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2c2，那么这个三角形就是直角三角形掌握定理是解题的关键19（8分）列二元一次方程组解
23、应用题：学校计划为“我和我的祖国”演讲比赛购买奖品已知购买3个A奖品和2个B奖品共需120元；购买5个A奖品和4个B奖品共需210元求A，B两种奖品的单价【分析】设A奖品的单价为x元，B奖品的单价为y元，根据“购买3个A奖品和2个B奖品共需120元；购买5个A奖品和4个B奖品共需210元”，即可得出关于x，y的二元一次次方程组，解之即可得出结论【解答】解：设A奖品的单价为x元，B奖品的单价为y元，依题意，得：，解得：答：A奖品的单价为30元，B奖品的单价为15元【点评】本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键四、（每小题8分，共16分）20（8分）甲、乙
24、、丙三位运动员在相同条件下各射靶10次，每次射靶的成绩如下：甲：9，10，8，5，7，8，10，8，8，7；乙：5，7，8，7，8，9，7，9，10，10；丙：7，6，8，5，4，7，6，3，9，5（1）根据以上数据完成下表：平均数中位数方差甲882乙882.2丙663（2）依据表中数据分析，哪位运动员的成绩最稳定，并简要说明理由【分析】（1）根据方差公式S2（x1）2+（x2）2+（xn）2，代值计算即可求出甲的方差；先把丙运动员的射靶成绩从小到大排列，再找出最中间的数即可得出答案；（2）根据方差的定义，方差越小数据越稳定【解答】解：（1）甲的平均数是8，甲的方差为：（58）2+2（78）2
25、+4（88）2+（98）2+2（108）22；把丙运动员的射靶成绩从小到大排列为：3，4，5，5，6，6，7，7，8，9，则中位数是6；故答案为：2，6；（2）甲的方差乙的方差丙的方差，而方差越小，数据波动越小，甲的成绩最稳定【点评】本题考查方差的定义：一般地设n个数据，x1，x2，xn的平均数为，则方差S2（x1）2+（x2）2+（xn）2，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立21（8分）如图，已知：ABC，A52，ACB56，点D，E分别在AB，AC上，连接DE，且ADE72，F是AD上一点，FE的延长线交BC的延长线于点G（1）求证：DEBC；（2）求证：EGHA
26、DE【分析】（1）由三角形内角和定理求出B72，得出BADE，即可得出结论；（2）根据平行线的性质得出BADE，根据三角形的外角性质得出EGHB，即可得出答案【解答】（1）证明：A52，ACB56，B180AACB72，ADE72，BADE，DEBC；（2）证明：EGH是FBG的外角，EGHB，又DEBC，BADEEGHADE【点评】本题考查了平行线的判定与性质、三角形内角和定理、三角形的外角性质等知识；熟练掌握平行线的判定与性质是解题的关键五、（本题10分）22（10分）如图，在ABC中，C90，A30，AB的垂直平分线交AB，AC于点D，E（1）求证：AE2CE；（2）当DE1时，求ABC
27、的面积【分析】（1）连接BE，由在ABC中，C90，A30，可求得ABC的度数，又由AB的垂直平分线交AB于点D，交AC于点E，根据线段垂直平分线的性质，可得AEBE，继而可求得CBE的度数，然后由含30角的直角三角形的性质，证得AE2CE（2）连接EB，根据线段垂直平分线的性质得到EAEB，求出EBC30，根据直角三角形的性质求出BE，根据勾股定理求出BC，根据三角形的面积公式计算，得到答案【解答】（1）证明：连接BEDE是AB的垂直平分线，AEBE，ABEA30，C90，ABC903060，CBEABCABE30，在RtBCE中，BE2CE，AE2CE；（2）ACB90，A30，ABC60
28、，DE是AB边的垂直平分线，EAEB，EBAA30，EBC30，EB2ED2，ECBE1，BCEC，ABC的面积BCAC3【点评】本题考查的是直角三角形的性质、线段垂直平分线的性质，掌握在直角三角形中，30角所对的直角边等于斜边的一半是解题的关键六、（本题10分）23（10分）已知：如图1，在平面直角坐标系中，长方形OABC的顶点B的坐标是（6，4）（1）直接写出A点坐标（6，0），C点坐标（0，4）；（2）如图2，D为OC中点连接BD，AD，如果在第二象限内有一点P（m，1），且四边形OADP的面积是ABC面积的2倍，求满足条件的点P的坐标；（3）如图3，动点M从点C出发，以每钞1个单位的速
29、度沿线段CB运动，同时动点N从点A出发以每秒2个单位的速度沿线段AO运动，当N到达O点时，M，N同时停止运动，运动时间是t秒（t0），在M，N运动过程中当MN5时，直接写出时间t的值【分析】（1）根据长方形的性质直接得出结论；（2）先求出ABC的面积，进而求出OAD的面积，进而得出ODP的面积，再求出OD，即可得出结论；（3）先用t表示出ON，CM，进而表示出HN，利用勾股定理建立方程求解即可得出结论【解答】解：（1）四边形OABC是长方形，ABOC，BCOA，B（6，4），A（6，0），C（0，4），故答案为：6，0，0，4；（2）如图2，由（1）知，A（6，0），C（0，4），OA6，OC
30、4，四边形OABC是长方形，S长方形OABCOAOC6424，连接AC，AC是长方形OABC的对角线，SOACSABCS长方形OABC12，点D是OC的中点，SOADSOAC6，四边形OADP的面积是ABC面积的2倍，S四边形OADP2SABC24，S四边形OADPSOAD+SODP6+SODP24，SODP18，点D是OC的中点，且OC4，ODOC2，P（m，1），SODPOD|m|2|m|18，m18（由于点P在第二象限，所以，m小于0，舍去）或m18，P（18，1）；（3）如图3，由（2）知，OA6，OC4，四边形OABC是长方形，AOCOCB90，BC6，由运动知，CMt，AN2t，O
31、NOAAN62t，过点M作MHOA于H，OHM90AOCOCB，四边形OCMH是长方形，MHOC4，OHCMt，HN|ONCM|62tt|63t|，在RtMHN中，MN5，根据勾股定理得，HN2MN2MH2，|63t|252429，t1或t3，即：t的值为1或3【点评】此题是四边形综合题，主要考查了长方形的性质，勾股定理，三角形面积的求法，掌握坐标系中求三角形面积的方法是解本题的关键七、（本题12分）24（12分）如图，在平面立角坐标系xOy中，直线AB与x轴，y轴分别交于点A（3，0）、点B（0，4），点C在y轴的负半轴上，若将CAB沿直线AC折叠，点B恰好落在x轴正半轴上的点D处（1）直接
32、写出AB的长5；（2）求直线AB的函数表达式；（3）求点D和点C的坐标；（4）y轴上是否存在一点P，使得SPABSOCD？若存在，直接写出点P的坐标；若不存在，请说明理由【分析】（1）AB5；（2）将点A、B的坐标代入一次函数表达式ykx+b，即可求解；（3）由题意得：ADAB5，故点D（8，0），设点C的坐标为：（0，m），而CDBC，即4m，解得：m6，即可求解；（4）SOCDCOOD6812，SABPBPxA|4m|312，即可求解【解答】解：（1）AB5，故答案为：5；（2）将点A、B的坐标代入一次函数表达式：ykx+b并解得：直线AB的表达式为：；（3）由题意得：ADAB5，故点D（
33、8，0），设点C的坐标为：（0，m），而CDBC，即4m，解得：m6，故点C（0，6）；（4）设点P（0，n），SOCDCOOD6812，SABPBPxA|4m|312，解得：m12或4，故P（0，12），（0，4）【点评】本题考查的是一次函数综合运用，涉及到图象折叠、面积的计算等，其中（4），要注意分类求解，避免遗漏八、（本题12分）25（12分）如图1，已知RtABC，ACB90，BAC30，斜边AB4，ED为AB垂直平分线，且DE2，连接DB，DA（1）直接写出BC2，AC2；（2）求证：ABD是等边三角形；（3）如图2，连接CD，作BFCD，垂足为点F，直接写出BF的长；（4）P是直线
34、AC上的一点，且CPAC，连接PE，直接写出PE的长【分析】（1）在RtABC中，解直角三角形求出BC，AC即可（2）通过计算证明DBDA4即可解决问题（3）利用面积法SBCDSABC+SABDSACD，构建方程即可解决问题（4）分两种情形分别求解：如图3中，延长DE交AC于P，连接PB证明点P满足条件，求出PE即可当CPAC时，作EHAC于H再利用勾股定理求出PH，EH即可解决问题【解答】（1）解：如图1中，在RtABC中，ACB90，BAC30，AB4，BCAB2，AC2故答案为2，（2）证明：如图1中，DE垂直平分AB，AEEB2，ADDB4，ABBDAD4，ABD是等边三角形（3）解：如图2中，ABD是等边三角形，BAD60，BAC30，CAD90，CD2，SBCDSABC+SABDSACD，2BF22+4242，BF（4）如图3中，延长DE交AC于P，连接PBDP垂直平分线段AB，PBPA，PBC30，C90，PB2PC，PA2PC，PCAC满足条件，PEAEtan30当CPAC时，作EHAC于H则EHAE1，PH，PH+，PE【点评】本题属于三角形综合题，考查了等边三角形的判定和性质，解直角三角形，三角形的面积等知识，解题的关键是学会利用面积法解决问题，学会用分类讨论的思想思考问题，属于中考常考题型
