1、2019年浙江省温州实验中学中考数学一模试卷一选择题（共10小题）1给出四个实数0、3，其中无理数是（）ABC0D32剪纸是中国古老的民间艺术，下列作品中既是轴对称图形，又是中心对称图形的是（）ABCD3流浪地球作为第一部中国自己的科幻大片，票房已破46亿元（4600000000），4600000000科学记数法表示为（）A46108B4.6108C0.46109D4.61094下列运算正确的是（）A（x3）3x6Bx3x2x5C3xx3Dx4+x2x65在体育模拟考中，某6人小组的1000米长跑得分（单位：分）分别为：10，9，8，10，10，9，则这组数据的众数和中位数分别是（）A9分，8
2、分B9分，9.5分C10分，9分D10分，9.5分6如图，将一副三角尺叠放在一起，使直角的顶点重合于点O，DC与OB交于点E，若ABOC，则CEB的度数为（）A95B100C105D1107已知点A（x+3，2x4）在第四象限，则x的取值范围是（）A3x2Bx3Cx2Dx28如图，在矩形纸片ABCD中，AB3，点E在BC上，将ABE沿AE折叠，点B恰好落在CD边上点F处，且CF1则tanCFE的值为（）ABCD9如图，直线yx+b（b2）与x轴，y轴分别交于H，G两点，边长为2的正方形OABC的边OA，OC分别在x轴，y轴上，点B在第一象限，正方形OABC绕点B逆时针旋转，OA的对应边OA恰好
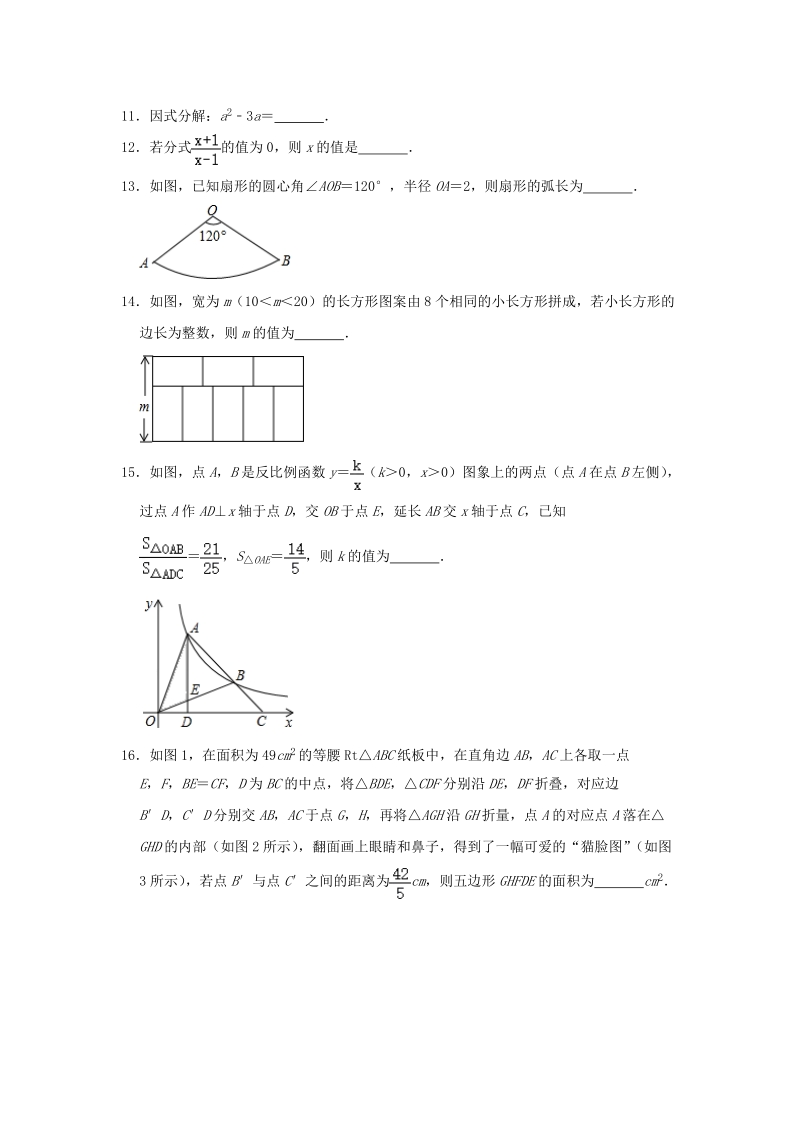
3、落在直线GH上，则b的值为（）A4BC5D610如图以正五边形ABCDE的顶点A为圆心，AE为半径作圆弧交BA的延长线于点A，再以点B为圆心，BA为半径作圆弧交CB的延长线于B，依次进行得到螺旋线，再顺次连结EA，AB，BC，CD，DE，得到5块阴影区域，若记它们的面积分别为S1，S2，S3，S4，S5，且满足S5S21，则S4S3的值为（）ABCD二填空题（共6小题）11因式分解：a23a 12若分式的值为0，则x的值是 13如图，已知扇形的圆心角AOB120，半径OA2，则扇形的弧长为 14如图，宽为m（10m20）的长方形图案由8个相同的小长方形拼成，若小长方形的边长为整数，则m的值为
4、15如图，点A，B是反比例函数y（k0，x0）图象上的两点（点A在点B左侧），过点A作ADx轴于点D，交OB于点E，延长AB交x轴于点C，已知，SOAE，则k的值为 16如图1，在面积为49cm2的等腰RtABC纸板中，在直角边AB，AC上各取一点E，F，BECF，D为BC的中点，将BDE，CDF分别沿DE，DF折叠，对应边BD，CD分别交AB，AC于点G，H，再将AGH沿GH折量，点A的对应点A落在GHD的内部（如图2所示），翻面画上眼睛和鼻子，得到了一幅可爱的“猫脸图”（如图3所示），若点B与点C之间的距离为cm，则五边形GHFDE的面积为 cm2三解答题（共8小题）17（1）计算：+（3
5、）0tan45（2）化简：（x2）2x（x1）182019年1月，温州轨道交通S1线正式运营，S1线有以下4种购票方式：A二维码过闸 B、现金购票 C、市名卡过闸 D、银联闪付（1）某兴趣小组为了解最受欢迎的购票方式，随机调查了某区的若干居民，得到如图所示的统计图，已知选择方式D的有200人，求选择方式A的人数（2）小博和小雅对A，B，C三种购票方式的喜爱程度相同，随机选取一种方式购票，求他们选择同一种购票方式的概率（要求列表或画树状图）19如图，ABC的顶点是方格纸中的三个格点，请按要求完成下列作图，仅用无刻度直尺，且不能用直尺中的直角；保留作图痕迹（1）在图1中画出AB边上的中线CD；（2
6、）在图2中画出ABEF，使得SABEFSABC20如图，在菱形ABCD中，点E，F分别在BC，CD上，且CECF，（1）求证ABEADF（2）若B50，AEBC，求AEF的度数21如图，抛物线yx2+bx+c过等腰RtOAB的A，B两点，点B在点A的右侧，直角顶点A（0，3）（1）求b，c的值（2）P是AB上方抛物线上的一点，作PQAB交OB于点Q，连接AP，是否存在点P，使四边形APQO是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由22如图，在ABC中，ABAC，BAC90，以AB为直径的O交BC于点F，连结OC，过点B作BDOC交O点D连接AD交OC于点E（1）求证：BDAE
7、（2）若OE1，求DF的值23如图，某校准备给长12米，宽8米的矩形ABCD室内场地进行地面装饰，现将其划分为区城I（菱形PQFG），区域（4个全等的直角三角形），剩余空白部分记为区，点O为矩形和菱形的对称中心，OPAB，OQ2OP，AEPM，为了美观，要求区域的而积不超过矩形ABCD面积的，若设OPx米（1）当x时，求区域的面积（2）计划在区域，分别铺设甲，乙两款不同的深色瓷砖，区域铺设丙款白色瓷砖，在相同光照条件下，当场地内白色区域的面积越大，室内光线亮度越好当x为多少时，室内光线亮度最好，并求此时白色区域的面积三种瓷砖的单价列表如下，m，n均为正整数，若当x2米时，购买三款瓷砖的总费用最
8、少，且最少费用为7200元，此时m ，n 甲乙丙单价（元/米2）2m5n2m24如图，在锐角ABC中，BC10，AC11，ABC的面积为33，点P是射线CA上一动点，以BP为直径作圆交线段AC于点E，交射线BA于点D，交射线CB于点F（1）当点P在线段AC上时，若点E为中点，求BP的长（2）连结EF，若CEF为等腰三角形，求所有满足条件的BP值（3）将DE绕点D顺时针旋转90，当点E的对应点E恰好落在BC上时，记DBE的面积为S1，DPE的面积S2，则的值为 （直接写出答案即可）参考答案与试题解析一选择题（共10小题）1给出四个实数0、3，其中无理数是（）ABC0D3【分析】分别根据无理数、有
9、理数的定义即可判定选择项【解答】解：A、是无理数，故本选项符合题意；B、是有理数，不是无理数，故本选项不符合题意；C、0是有理数，不是无理数，故本选项不符合题意；D、3是有理数，不是无理数，故本选项不符合题意；故选：A2剪纸是中国古老的民间艺术，下列作品中既是轴对称图形，又是中心对称图形的是（）ABCD【分析】根据轴对称图形与中心对称图形的概念求解【解答】解：A、不是轴对称图形，也不是中心对称图形，故此选项不合题意；B、是轴对称图形，也是中心对称图形，故此选项符合题意；C、不是轴对称图形，也不是中心对称图形，故此选项不合题意；D、不是轴对称图形，也不是中心对称图形，故此选项不合题意故选：B3流
10、浪地球作为第一部中国自己的科幻大片，票房已破46亿元（4600000000），4600000000科学记数法表示为（）A46108B4.6108C0.46109D4.6109【分析】科学记数法的表示形式为a10n的形式，其中1|a|10，n为整数确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同当原数绝对值1时，n是正数；当原数的绝对值1时，n是负数【解答】解：4600000000科学记数法表示为4.6109故选：D4下列运算正确的是（）A（x3）3x6Bx3x2x5C3xx3Dx4+x2x6【分析】直接利用积的乘方运算法则以及同底数幂的乘法运算法则、合并同
11、类项法则分别判断得出答案【解答】解：A、（x3）3x9，故此选项错误；B、x3x2x5，正确；C、3xx2x，故此选项错误；D、x4+x2，无法计算，故此选项错误；故选：B5在体育模拟考中，某6人小组的1000米长跑得分（单位：分）分别为：10，9，8，10，10，9，则这组数据的众数和中位数分别是（）A9分，8分B9分，9.5分C10分，9分D10分，9.5分【分析】根据众数和中位数的概念求解可得【解答】解：将数据重新排列为8，9，9，10，10，10，这组数据的众数为9，中位数为9.5，故选：B6如图，将一副三角尺叠放在一起，使直角的顶点重合于点O，DC与OB交于点E，若ABOC，则CEB
12、的度数为（）A95B100C105D110【分析】依据平行线的性质，即可得到BBOC45，再根据三角形外角性质，即可得到CEB的度数【解答】解：ABOC，BBOC45，又C60，CEBBOC+C45+60105，故选：C7已知点A（x+3，2x4）在第四象限，则x的取值范围是（）A3x2Bx3Cx2Dx2【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集【解答】解：由题意知，解不等式，得：x3，解不等式，得：x2，则不等式组的解集为3x2，故选：A8如图，在矩形纸片ABCD中，AB3，点E在BC上，将ABE沿AE折叠，点B恰好落在
13、CD边上点F处，且CF1则tanCFE的值为（）ABCD【分析】由矩形的性质可得ABCD3，ADBC，DFCDCF2，由折叠的性质可得AFAB3，AFEABE90，由勾股定理可求AD的长，由余角的性质可得CFEDAF，即可求解【解答】解：四边形ABCD是矩形ABCD3，ADBC，CF1DFCDCF2将ABE沿AE折叠，AFAB3，AFEABE90ADAFE90CFE+AFD90，且DAF+DFA90CFEDAFtanCFEtanDAF故选：D9如图，直线yx+b（b2）与x轴，y轴分别交于H，G两点，边长为2的正方形OABC的边OA，OC分别在x轴，y轴上，点B在第一象限，正方形OABC绕点B
14、逆时针旋转，OA的对应边OA恰好落在直线GH上，则b的值为（）A4BC5D6【分析】过点A作AMx轴，过点B作BMy轴，相交于点M；可以证明BAMH，在RtABM中，AB2，tanBAM，分别求出BM，AM，确定A的坐标为A（，），再将点A（，）代入yx+b，即可求解【解答】解：过点A作AMx轴，过点B作BMy轴，在RtABM，BAM+ABMBAM+MAO90，H+HAM90，BAMH，tanBAM，AB2，BM，AM，B（2，2），A（，），将点A（，）代入yx+b，b5；故选：C10如图以正五边形ABCDE的顶点A为圆心，AE为半径作圆弧交BA的延长线于点A，再以点B为圆心，BA为半径作圆
15、弧交CB的延长线于B，依次进行得到螺旋线，再顺次连结EA，AB，BC，CD，DE，得到5块阴影区域，若记它们的面积分别为S1，S2，S3，S4，S5，且满足S5S21，则S4S3的值为（）ABCD【分析】设五边形的边长为a求出各个阴影部分的面积，根据S5S21，寻找关系式，即可解决问题【解答】解：设五边形的边长为a则S1a2sin72，S2a2asin72，S3a3asin72，S4a4asin72，S5a5asin72，S5S21，5a2a2a2sin721，a2a2sin721，S4S3a2a2a2sin72a2a2sin72，故选：D二填空题（共6小题）11因式分解：a23aa（a3）【
16、分析】直接把公因式a提出来即可【解答】解：a23aa（a3）故答案为：a（a3）12若分式的值为0，则x的值是1【分析】分式的值为0的条件是：（1）分子为0；（2）分母不为0两个条件需同时具备，缺一不可据此可以解答本题【解答】解：由分式的值为0，得x+10且x10解得x1，故答案为：113如图，已知扇形的圆心角AOB120，半径OA2，则扇形的弧长为【分析】利用弧长公式直接计算AB的弧长【解答】解：由弧长公式得：扇形的弧长；故答案为：14如图，宽为m（10m20）的长方形图案由8个相同的小长方形拼成，若小长方形的边长为整数，则m的值为16【分析】设小长方形的长为x，宽为y，根据长方形的对边相等
17、即可得出关于x，y的二元一次方程，结合x，y均为整数可得出x为5的倍数且y为3的倍数，再结合（x+y）的取值范围，即可求出结论【解答】解：设小长方形的长为x，宽为y，依题意，得：3x5y，x，y均为整数，x为5的倍数，y为3的倍数，10x+y20，x10，y6，mx+y16故答案为：1615如图，点A，B是反比例函数y（k0，x0）图象上的两点（点A在点B左侧），过点A作ADx轴于点D，交OB于点E，延长AB交x轴于点C，已知，SOAE，则k的值为【分析】根据反比例函数中k的几何意义，可得SOAD|k|，即可求出k的值【解答】解：作BFx轴于F，OD：DF：FC2：3：2，SOAE，SOAD，
18、|k|，k0，k故答案为：16如图1，在面积为49cm2的等腰RtABC纸板中，在直角边AB，AC上各取一点E，F，BECF，D为BC的中点，将BDE，CDF分别沿DE，DF折叠，对应边BD，CD分别交AB，AC于点G，H，再将AGH沿GH折量，点A的对应点A落在GHD的内部（如图2所示），翻面画上眼睛和鼻子，得到了一幅可爱的“猫脸图”（如图3所示），若点B与点C之间的距离为cm，则五边形GHFDE的面积为cm2【分析】如图，连接AD，BC，AD交GH于J，交BC于H，作FPCD于P在RtDHB中，利用勾股定理求出DQ，tanQDC，设JH3a，JD4a，则AJJH3a，构建方程求出a，再证明
19、tanFDP，构建方程求出FP即可解决问题【解答】解：如图，连接AD，BC，AD交GH于J，交BC于H，作FPCD于PABAC，BAC90，BDDC，ADBC，ADBDCD，SABCBCADAD249，ADBDCD7，由题意：BQCQ，在RtDHB中，DQ，tanQDC，设JH3a，JD4a，则AJJH3a，7a7，a1，JHAJ3，DJ4，由右图可知：tan，tanFDP，设CPPFm，则DP2m，3m7，m，S五边形GHFDESABCSAHG2SDFC496327，故答案为三解答题（共8小题）17（1）计算：+（3）0tan45（2）化简：（x2）2x（x1）【分析】（1）根据实数的混合运
20、算法则计算；（2）根据单项式乘多项式的运算法则、完全平方公式计算【解答】解：（1）+（3）0tan455+115；（2）（x2）2x（x1）x24x+4x2+x3x+4182019年1月，温州轨道交通S1线正式运营，S1线有以下4种购票方式：A二维码过闸 B、现金购票 C、市名卡过闸 D、银联闪付（1）某兴趣小组为了解最受欢迎的购票方式，随机调查了某区的若干居民，得到如图所示的统计图，已知选择方式D的有200人，求选择方式A的人数（2）小博和小雅对A，B，C三种购票方式的喜爱程度相同，随机选取一种方式购票，求他们选择同一种购票方式的概率（要求列表或画树状图）【分析】（1）先求出样本容量，再用样
21、本容量乘以A对应的比例即可得；（2）列表得出所有等可能结果，从中找到符合条件的结果数，再利用概率公式求解可得【解答】解：（1）被调查的总人数为2001800（人），选择方式A的人数为1800600（人）；（2）列表如下：ABCA（A，A）（B，A）（C，A）B（A，B）（B，B）（C，B）C（A，C）（B，C）（C，C）由表可知共有9种等可能的结果，其中他们选中同一种购票方式的有3种情况，所以他们选择同一种购票方式的概率为19如图，ABC的顶点是方格纸中的三个格点，请按要求完成下列作图，仅用无刻度直尺，且不能用直尺中的直角；保留作图痕迹（1）在图1中画出AB边上的中线CD；（2）在图2中画出A
22、BEF，使得SABEFSABC【分析】（1）利用平行线等分线段定理得到线段AB的中点D，即可解决问题（2）取AC的中点F，连接BF，取格点H，利用平行线的性质解决问题即可【解答】解：（1）如图线段CD即为所求（2）如图，四边形ABEF的面积即为所求理由：取AC的中点F，连接BF，取格点H，CHBF，SBFCSBFE，S四边形ABEFSABC20如图，在菱形ABCD中，点E，F分别在BC，CD上，且CECF，（1）求证ABEADF（2）若B50，AEBC，求AEF的度数【分析】（1）由“SAS”可证ABEADF；（2）由菱形的性质可求C110，由余角的性质可求CEF的值，即可求AEF的值【解答】
23、证明：（1）四边形ABCD是菱形ABADBCCD，BD，ABCDCECFBEDF，且BD，ABAD，ABEADF（SAS）（2）ABCDB+C180，且B50C130，且CECFCEF25AEBCAEF90256521如图，抛物线yx2+bx+c过等腰RtOAB的A，B两点，点B在点A的右侧，直角顶点A（0，3）（1）求b，c的值（2）P是AB上方抛物线上的一点，作PQAB交OB于点Q，连接AP，是否存在点P，使四边形APQO是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由【分析】（1）根据题意得到点B的坐标，把A，B的坐标代入二次函数解析式，列出关于系数b、c的方程组，通过解方程
24、组可以求得它们的值；（2）由条件可知OAPQ，则PQ3时，OAPQ为平行四边形，设P（m，m2+3m+3），Q（m，m），可得关于m的方程，求出m的值即可求解【解答】解：（1）A（0，3），等腰RtOAB，AB3OA，B（3，3），将点A、B的坐标代入yx2+bx+c得：，（2）存在，B（3，3），OB的解析式为yx，yx2+3x+3，设P（m，m2+3m+3），Q（m，m），PQAB，OAAB，OAPQ，若四边形APQO是平行四边形，PQm2+3m+3m3，解得m0（舍去），m2，当m2时，y4+6+35，p（2，5），即当P（2，5）时，四边形APQO是平行四边形22如图，在ABC中，AB
25、AC，BAC90，以AB为直径的O交BC于点F，连结OC，过点B作BDOC交O点D连接AD交OC于点E（1）求证：BDAE（2）若OE1，求DF的值【分析】（1）证明ADBCEA（AAS），即可解决问题（2）利用相似三角形的性质求解即可解决问题【解答】（1）证明：AB是直径，ADB90，BDOC，AEOADB90，OAC90，OAE+AOC90，AOC+ACO90，BADACE，ABAC，ADBAEC90，ADBCEA（AAS），AEBD（2）OEBD，AOOB，AEED，BD2OE2，AEBDDE2，AB2，ADBCEA，ECAD4，设AD交BC于KECBD，2，DK，BK，ABKFDK，A
26、KBFKD，AKBFKD，DF23如图，某校准备给长12米，宽8米的矩形ABCD室内场地进行地面装饰，现将其划分为区城I（菱形PQFG），区域（4个全等的直角三角形），剩余空白部分记为区，点O为矩形和菱形的对称中心，OPAB，OQ2OP，AEPM，为了美观，要求区域的而积不超过矩形ABCD面积的，若设OPx米（1）当x时，求区域的面积（2）计划在区域，分别铺设甲，乙两款不同的深色瓷砖，区域铺设丙款白色瓷砖，在相同光照条件下，当场地内白色区域的面积越大，室内光线亮度越好当x为多少时，室内光线亮度最好，并求此时白色区域的面积三种瓷砖的单价列表如下，m，n均为正整数，若当x2米时，购买三款瓷砖的总费
27、用最少，且最少费用为7200元，此时m40，n8甲乙丙单价（元/米2）2m5n2m【分析】（1）求出四个直角三角形的面积的和即可（2）构建二次函数，利用二次函数的性质解决问题即可构建一次函数确定m与n的关系，再构建二元一次方程，确定整数解即可判断【解答】解：（1）由题意AMDM6米，AEPM（4），区域的面积468（平方米）（2）白色区域的面积8122x4x46（4x）4（x）2+，40，2x3，x2时，白色区域的面积最大，最大值为68设总费用为w元则W2m2x4x+5n4（4x）6+2m964x2（246x）（12m30n）x+144m+120n，2x3，x2时，购买三款瓷砖的总费用最少，1
28、2m30n0，mn，当x2时，区域的面积为4816，（平方米）区域的面积为46112（平方米），区域的面积为68（平方米），由题意：162m+125n+682m7200，14m+5n600，m，n是正整数，解得，mn，符合条件的m40，n8故答案为：40，824如图，在锐角ABC中，BC10，AC11，ABC的面积为33，点P是射线CA上一动点，以BP为直径作圆交线段AC于点E，交射线BA于点D，交射线CB于点F（1）当点P在线段AC上时，若点E为中点，求BP的长（2）连结EF，若CEF为等腰三角形，求所有满足条件的BP值（3）将DE绕点D顺时针旋转90，当点E的对应点E恰好落在BC上时，记D
29、BE的面积为S1，DPE的面积S2，则的值为（直接写出答案即可）【分析】（1）先利用面积求高BE，再由勾股定理求AB、AE、CE，再根据全等三角形判定和性质求得PB；（2）CEF为等腰三角形，可以分三种情况：CFEF，过F作FGAC于点G，连接PF，利用相似三角形性质即可得到答案；EFCE，过E作EGCB于G，连接EF、BP，利用全等三角形判定和性质即可；CECF，利用全等三角形判定、性质和勾股定理即可；（3）过点E作EMDP于点M，过E作EGAC于点G，作ENAB于点N，过D作DFAC于点F，作DHEG于点H，依次证明：DFGH是矩形，DEFDEH（AAS），EDNEDM（AAS），再运用由
30、相似三角形性质和解直角三角形知识即可【解答】解：（1）如图1，连接BE、DE，BP为直径，BECBEA90BC10，AC11，ABC的面积为33，ACBE33BE6CE8AEACCE3AB3点E为中点ABEPBEBEBEABEPBE（ASA）BPAB3（2）CEF为等腰三角形，可以分三种情况：CFEF，如图2，过F作FGAC于点G，连接PF，BP是直径BFPCFPCGFCEB90EGCGCF4FGBECFGCBECPF，即CF5，即CPEPCECP8BPEFCE，如图3，过E作EGCB于G，连接EF、BP，则CGGFEFGCBPEEFGCBPECEBPEB90，BEBECBEPBE（AAS）B
31、PBC10CECF，如图4，连接EF、BP、BE、AF，BP为直径AFBAEB90CCCEBCFP（ASA）CPCB10PE2BP2综上所述，满足条件的BP值为：或10或2（3）如图5，过点E作EMDP于点M，过E作EGAC于点G，作ENAB于点N，过D作DFAC于点F，作DHEG于点H，DFAC，DHEG，EGACDFEDHEEGF90DFGH是矩形，GHDF FGDHFDH90EDF+EDH90EDH+EDH90EDFEDHDEDEDEFDEH（AAS）DFDH，EFEHDFBE，设AFm，则：DFDHGHFG2m，EFEH3mEGm+3，AG3m，CGCAAG113m，tanC，即：4EG3CG4（m+3）3（113m），解得：mEF3，DF2BP是直径，EDN+EDP90，EDP+EDM90EDNEDMEDNEDM（AAS）ENEMtanBPDBEDBPDDFBEBEDEDFBPDEDFtanBPDtanEDF，故答案为：
