 2018-2019学年山东省菏泽市高二(下)期末数学试卷(含详细解答)
2018-2019学年山东省菏泽市高二(下)期末数学试卷(含详细解答)
《2018-2019学年山东省菏泽市高二(下)期末数学试卷(含详细解答)》由会员分享,可在线阅读,更多相关《2018-2019学年山东省菏泽市高二(下)期末数学试卷(含详细解答)(21页珍藏版)》请在七七文库上搜索。
1、2018-2019学年山东省菏泽市高二(下)期末数学试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1(5分)集合Ax|x2x20,Bx|x10,则AB()Ax|x1Bx|1x1Cx|x2Dx|2x12(5分)已知i是虚数单位,z,则复数Z的共轭复数为()A1+iB1iC1iD1+i3(5分)命题“x0,+),x2+x0”的否定是()Ax(0,+),x2+x0Bx(,0)x2+x0Cx00,+),x02+x00Dx00,+),x02+x004(5分)(2+x)4的展开式中,x3的系数为()A2B4C6D85(5分)已知函数(e2.71
2、828是自然对数的底数)当x0时有唯一的零点,则该零点所在的区间是()A(1,0)B(0,1)C(1,2)D(2,e)6(5分)给出四个函数,分别满足:f(x+y)f(x)+f(y);g(x+y)g(x)g(y);h(xy)h(x)+h(y);t(xy)t(x)t(y)又给出四个函数图象正确的匹配方案是()A丁乙丙甲B乙丙甲丁C丙甲乙丁D丁甲乙丙7(5分)某地区空气质量检测资料表明,一天的空气质量为优良的概率是0.9,连续两天为优良的概率是0.75,已如某天的空气质量为优良,则随后一天的空气质量也为优良的概率为()ABCD8(5分)从4名男生和2名女生中任选3人参加演讲比赛,用x表示所选3人中
3、女生的人数,则E(X)为()A0B1C2D39(5分)函数f(x)在(,+)单调递减,且为奇函数若f(1)2,则满足2f(2x1)2的x的取值范围是()A2,2B1,1C0,1D1,210(5分)欧拉公式eixcosx+isinx(i为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉“数学中的天桥”,根据欧拉公式可知,表示的复数的虚部为()ABCD11(5分)已知y与x及与的成对数据如下,且y关于x的回归直线方程为1.2x+0.6,则关于的回归直线方程为()x12345y2345710203040
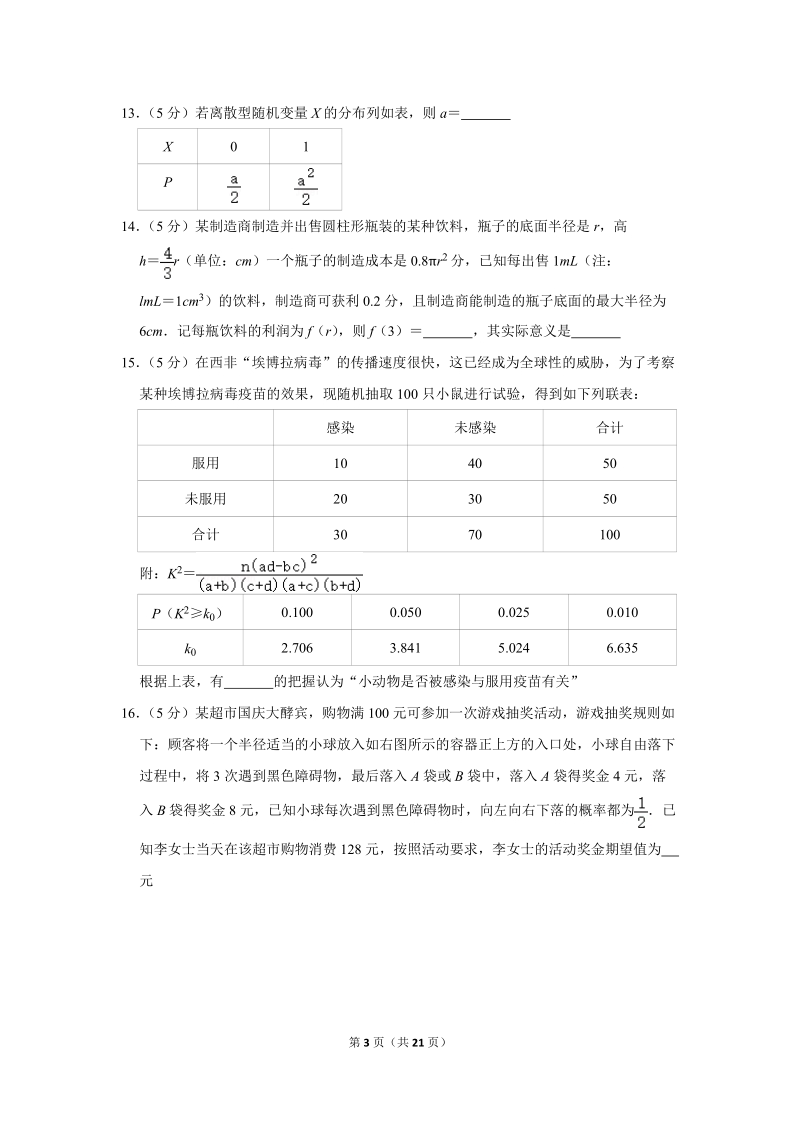
4、502030405070A12+6B1.2+0.6C0.12+0.6D1.2+612(5分)设函数f(x)ex2asinxx(0,)有且仅有一个零点,则实数a的值为()ABCD二、填空题(本大题共4个小题,每小题5分,共20分.)13(5分)若离散型随机变量X的分布列如表,则a X01P14(5分)某制造商制造并出售圆柱形瓶装的某种饮料,瓶子的底面半径是r,高hr(单位:cm)一个瓶子的制造成本是0.8r2分,已知每出售1mL(注:lmL1cm3)的饮料,制造商可获利0.2分,且制造商能制造的瓶子底面的最大半径为6cm记每瓶饮料的利润为f(r),则f(3) ,其实际意义是 15(5分)在西非“
5、埃博拉病毒”的传播速度很快,这已经成为全球性的威胁,为了考察某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:感染未感染合计服用104050未服用203050合计3070100附:K2P(K2k0)0.1000.0500.0250.010k02.7063.8415.0246.635根据上表,有 的把握认为“小动物是否被感染与服用疫苗有关”16(5分)某超市国庆大酵宾,购物满100元可参加一次游戏抽奖活动,游戏抽奖规则如下:顾客将一个半径适当的小球放入如右图所示的容器正上方的入口处,小球自由落下过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋得奖金4元,落入B
6、袋得奖金8元,已知小球每次遇到黑色障碍物时,向左向右下落的概率都为已知李女士当天在该超市购物消费128元,按照活动要求,李女士的活动奖金期望值为 元三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤17(10分)(1)设集合Ax|x25x+60,Bx|mx+10),且BA,求实数m的值;(2)设z1,z2是两个复数,已知z11+i,|z2|2,且z1,z2是实数,求z218(12分)已知函数f(x)x3+mx2+nx+10有两个极值点1和3(1)求m,n的值;(2)若函数f(x)的图象在点P(1,f(1)的切线为l,切线l与x轴和y轴分别交于A、B两点,点O为坐标原点
7、,求AOB的面积19(12分)假设某种人寿保险规定,投保人没活过65岁,保险公司要赔偿10万元若投保人活过65岁,则保险公司不赔偿,但要给投保人一次性支付4万元已知购买此种人寿保险的每个投保人能活过65岁的概率都为0.9,随机抽取4个投保人,设其中活过65岁的人数为X,保险公司支出给这4人的总金额为y万元(参考数据:0.940.6561)(1)指出X服从的分布并写出Y与X的关系:(2)求P(Y22)(结果保留3位小数)20(12分)习近平总书记在十九大报告中指出,必须树立和践行“绿水青山就是金山银山”的生态文明发展理念,某城市选用某种植物进行绿化,设其中一株幼苗从观察之日起,第x的高度为ycm
8、,测得一些数据图如下表所示第x天14916253649高度x/cm0479111213作出这组数的散点图如图(1)请根据散点图判断,yax+b与yc+d中哪一个更适宜作为幼苗高度y关于时间x的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程,并预测第144天这株幼苗的高度(结果保留1位小数)附:,参考数据:140285628321(12分)已知函数f(x)xln(x+m)的图象过点(1,0)(1)求f(x)的解析式及单调区间;(2)求f(x)在t,t+2(t0)上的最小值22(12分)某市一次全市高中男生身高统计调查数据显示:全市10万名
9、男生的身高服从正态分布N(,2)现从某学校高中男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和190cm之间,将身高的测量结果按如下方式分成5组:第1组60,166,第2组166,172),第5组184,190如表是按上述分组方法得到的频率分布表分组160,166)166,172)172,178)178,184)184,190)人数31024103这50个数据的平均数和方差分别比10万个数据的平均数和方差多1和668,且这50个数据的方差为s231.68,(同一组中的身高数据用该组区间的中点值作代表);(1)求,;(2)给出正态分布的数据:P(X+)0.6826 P(2X
10、+2)0.9544(i)若从这10万名学生中随机抽取1名,求该学生身高在(169,179)的概率;(ii)若从这10万名学生中随机抽取1万名,记X为这1万名学生中身高在(169,184)的人数,求X的数学期望2018-2019学年山东省菏泽市高二(下)期末数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1(5分)集合Ax|x2x20,Bx|x10,则AB()Ax|x1Bx|1x1Cx|x2Dx|2x1【分析】先分别求出集合A和B,由此能求出AB【解答】解:集合Ax|x2x20x|1x2,Bx|x10x|x1,AB
11、x|x2故选:C【点评】本题考查并集的求法,考查并集定义、不等式性质等基础知识,考查运算求解能力,是基础题2(5分)已知i是虚数单位,z,则复数Z的共轭复数为()A1+iB1iC1iD1+i【分析】把已知等式变形,再由复数代数形式的乘除运算化简得答案【解答】解:z,故选:A【点评】本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题3(5分)命题“x0,+),x2+x0”的否定是()Ax(0,+),x2+x0Bx(,0)x2+x0Cx00,+),x02+x00Dx00,+),x02+x00【分析】根据含有量词的命题的否定即可得到结论【解答】解:命题“x0,+),x2+x0”为全称命题,
12、则命题的否定为x00,+),x02+x00,故选:C【点评】本题主要考查含有量词的命题的否定,比较基础4(5分)(2+x)4的展开式中,x3的系数为()A2B4C6D8【分析】将二项式展开,找出所求项的系数即可【解答】解:(2+x)4+,所以8,故选:D【点评】本题考查二项式定理,对于简单的二项式可以直接展开求得结果,复杂的要利用通项公式求解5(5分)已知函数(e2.71828是自然对数的底数)当x0时有唯一的零点,则该零点所在的区间是()A(1,0)B(0,1)C(1,2)D(2,e)【分析】考虑f(x)为连续函数,计算f(1),f(0),f(1),f(2),f(e)的符号,由零点存在定理可
13、得所求区间【解答】解:f(x)exx为连续函数,且f(1)e1+10,f(0)100,f(1)e10,f(2)e220,f(e)eee0,可得f(x)在(0,1)存在零点,故选:B【点评】本题考查函数的零点存在定理的运用,考查运算能力,属于基础题6(5分)给出四个函数,分别满足:f(x+y)f(x)+f(y);g(x+y)g(x)g(y);h(xy)h(x)+h(y);t(xy)t(x)t(y)又给出四个函数图象正确的匹配方案是()A丁乙丙甲B乙丙甲丁C丙甲乙丁D丁甲乙丙【分析】f(x)x,这个函数可使 f(x+y)x+yf(x)+f(y)成立,故丁;指数函数yax(a0,a1)使得g(x+y
14、)g(x)g(y),故甲;令:h(x)logax,则h(xy)loga(xy)logax+logbx故乙t(x)x2,这个函数可使t(xy)t(x)t(y)成立故丙【解答】解:f(x)x,这个函数可使 f(x+y)x+yf(x)+f(y)成立,f(x+y)x+y,x+yf(x)+f(y),f(x+y)f(x)+f(y),自变量的和等于因变量的和正比例函数ykx就有这个特点故丁;寻找一类函数g(x),使得g(x+y)g(x)g(y),即自变量相加等于因变量乘积指数函数yax(a0,a1)具有这种性质:g(x)ax,g(y)ay,g(x+y)ax+yaxayg(x)g(y)故甲;自变量的乘积等于因
15、变量的和:与相反,可知对数函数具有这种性质:令:h(x)logax,则h(xy)loga(xy)logax+logbx故乙t(x)x2,这个函数可使t(xy)t(x)t(y)成立t(x)x2,t(xy)(xy)2x2y2t(x)t(y),故丙故选:D【点评】本题考查函数的图象的性质和应用,是基础题解题时要认真审题,仔细解答7(5分)某地区空气质量检测资料表明,一天的空气质量为优良的概率是0.9,连续两天为优良的概率是0.75,已如某天的空气质量为优良,则随后一天的空气质量也为优良的概率为()ABCD【分析】连续两天为优良的概率是0.75,某天的空气质量为优良,由条件概率公式可得随后一天的空气质
16、量也为优良的概率【解答】解:某地区空气质量检测资料表明,一天的空气质量为优良的概率是0.9,连续两天为优良的概率是0.75,某天的空气质量为优良,则随后一天的空气质量也为优良的概率为:P故选:A【点评】本题考查概率的求法,考查条件概率的等基础知识,考查了推理能力与计算能力,是基础题8(5分)从4名男生和2名女生中任选3人参加演讲比赛,用x表示所选3人中女生的人数,则E(X)为()A0B1C2D3【分析】由题意X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列然后求出X的均值E(X)【解答】解:从4名男生和2名女生中任选3人参加演讲比赛,设随机变量X表示所选3人中女生的人数,X的
17、可能取值为0,1,2,P(X0),P(X1),P(X2),X的分布列为: X 0 1 2 P X的均值E(X)0+1+21故选:B【点评】本题考查概率的求法,考查离散型随机变量的分布列、数学期望、方差的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用9(5分)函数f(x)在(,+)单调递减,且为奇函数若f(1)2,则满足2f(2x1)2的x的取值范围是()A2,2B1,1C0,1D1,2【分析】根据题意,由函数的奇偶性的性质可得f(1)2,结合函数的单调性可得2f(2x1)2f(1)f(2x1)f(1)12x11,解可得x的取值范围,即可得答案【解答】解:根据题意,f(x)为奇函数


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2018 2019 学年 山东省 菏泽市 期末 数学试卷 详细 解答
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-124807.html