1、2020中考数学培优专题：分类讨论题型训练（含答案）一、单选题（共有10道小题）1.一个等腰三角形的两边长分别是2和5，则它的周长是（ ）A7 B9 C12 D9或122.现有3cm，4cm，7cm，9cm长的四根木棒，任取其中三根组成一个三角形，那么可以组成的三角形的方案有()A.1个 B.2个 C.3个 D.4个3.如图，图中的三角形被木板遮住了一部分，这个三角形是（）A.锐角三角形B.直角三角形C.钝角三角形D.以上都有可能4.有一个数值转换器，原理如下：当输入的x为64时，输出的y是（ ） A.8B.C.D.5.已知等腰三角形一边长为4，另一边长为8，刚这个等腰三角形的周长为（ ）A.
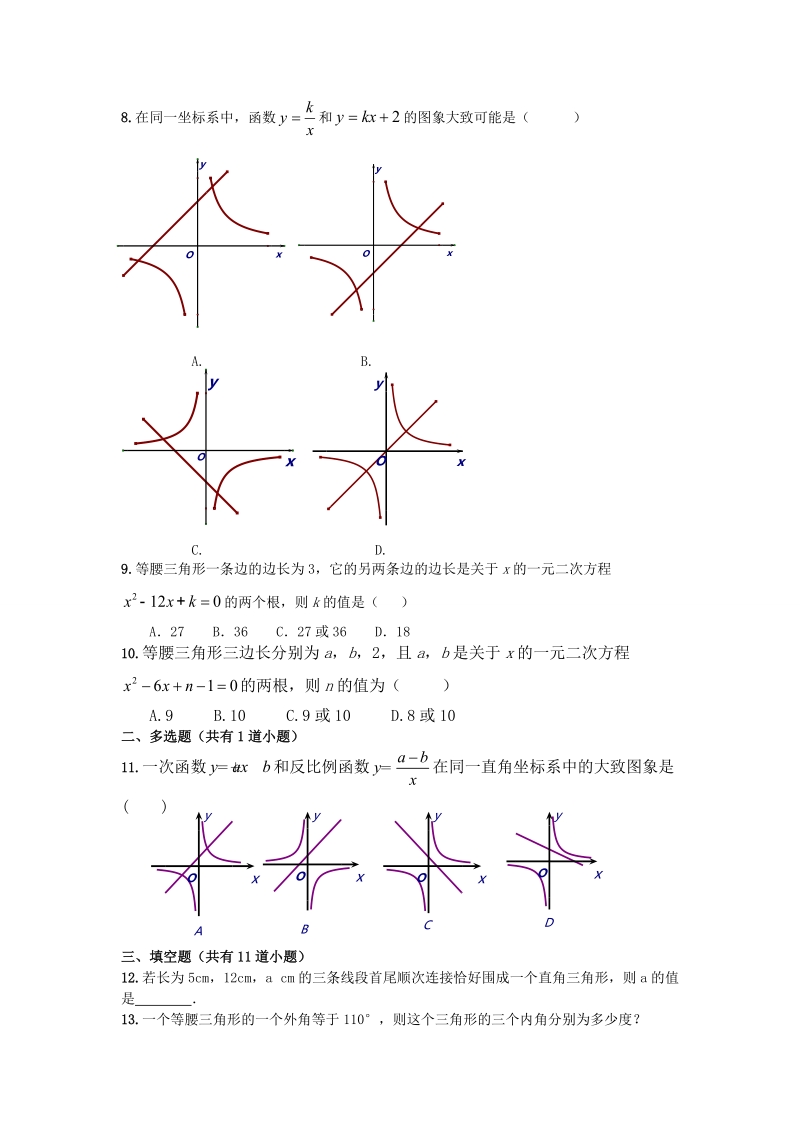
2、16B.20或16C.20D.126.若等腰三角形中有一个角等于50，则这个等腰三角形的顶角的度数为（ ）A50B80C65或50D50或807.一个多边形截去一个角后， 形成另一个多边形的内角和为720，那么原多边形的边数为（ ）A.5 B.5或6 C.5或7 D.5或6或78.在同一坐标系中，函数和的图象大致可能是（）A. B. C. D. 9.等腰三角形一条边的边长为3，它的另两条边的边长是关于x的一元二次方程的两个根，则k的值是（ ）A27 B36 C27或36 D1810.等腰三角形三边长分别为a，b，2，且a，b是关于x的一元二次方程的两根，则n的值为（ ）A.9 B.10 C.9
3、或10 D.8或10二、多选题（共有1道小题）11.一次函数和反比例函数在同一直角坐标系中的大致图象是()三、填空题（共有11道小题）12.若长为5cm，12cm，a cm的三条线段首尾顺次连接恰好围成一个直角三角形，则a的值是 13.一个等腰三角形的一个外角等于110，则这个三角形的三个内角分别为多少度？ 14.如图，在43的长方形网格中，已知A、B两点为格点（网格线的交点称为格点），若C也为该网格中的格点，且ABC为等腰直角三角形，则格点C可能的位置有 个15.如图，A=500，B=600，一直线l与ABC的边AC、AB边相交于点D、E两点，当ADE为_度时，ABC与ADE相似.16.已知
4、两条线段的长为5cm和12cm,当第三条线段的长 cm时,这三条线段能组成一个直角三角形.17.如图，正方形ABCD的边长为2，AE=EB，MN=1，线段MN的两端在CB、CD上滑动，当CM= 时，AED与以M、N、C为顶点的三角形相似。18.甲乙两地相距50千米星期天上午8：00小聪同学在父亲陪同下骑山地自行车从甲地前往乙地2小时后，小明的父亲骑摩托车沿同一路线也从甲地前往乙地，他们行驶的路程y（千米）与小聪行驶的时间x（小时）之间的函数关系如图所示，小明父亲出发_小时时，行进中的两车相距8千米19.如图，在梯形ABCD中，ADBC，A=60，动点P从A点出发，以1cm/s的速度沿着ABCD
5、的方向移动，直到点P到达点D后停止。已知PAD的面积S（平方厘米）与点P移动的时间t（秒）的函数如图，则点P从开始移动到停止移动一共用了 秒20.如果是一个完全平方公式，则 。21.阅读下列解题过程：已知a、b、c为ABC的三边，且满足，则ABC是 三角形.22.一组数据：的中位数和平均数相等，则的值是 。四、作图题（共有1道小题）23.如图是由三个阴影的小正方形组成的图形，请你在三个网格图中，各补画出一个有阴影的小正方形，使补画后的图形为轴对称图形21c五、解答题（共有10道小题）24.我市某医药公司把一批药品运往外地，现有两种运输方式可供选择：方式一：使用快递公司的邮车运输，装卸收费400
6、元，另外每公里再加收4元；方式二：使用快递公司的火车运输，装卸收费820元，另外每公里再加收2元.(1)请分别写出邮车、火车运输的总费用y1，y2(元)与运输路程x(公里)之间的函数关系；(2)你认为选用哪种运输方式较好，为什么？25.如图，已知直线经过点A（-1，0）与点B（2，3），另一条直线经过点 B，且与x轴相交于点P（m，0） （1）求直线的解析式 （2）若APB的面积为3，求m的值（提示：分两种情形，即点P在A的左侧和右侧）26.已知：如图，在梯形ABCD中，ADBC，AD=24cm，BC=30cm，点P自点A向D以1cm/s的速度运动，到D点即停止点Q自点C向B以2cm/s的速度
7、运动，到B点即停止，直线PQ截梯形为两个四边形问当P，Q同时出发，几秒后其中一个四边形为平行四边形？27.某景区的三个景点A，B，C在同一线路上，甲、乙两名游客从景点A出发，甲步行到景点C，乙乘景区观光车先到景点B，在B处停留一段时间后，再步行到景点C 甲、乙两人离开景点A后的路程S（米）关于时间t（分钟）的函数图象如图所示则乙出发后多长时间与甲相遇？28.已知一个等腰三角形的两角分别为(2x2)，(3x5)，求这个等腰三角形各角的度数29.如图，已知ABBD，CDBD。若AB=9，CD=4，BD=10，判断在BD上是否存在点P，使以P，A，B三点为顶点的三角形与以点P，C，D三点为顶点的三角
8、形相似？若存在，求BP的长；若不存在，请说明理由。30.如图，已知直线与轴交于点A，与x轴交于点D，抛物线与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为 (1，0)（1）求该抛物线的解析式；（2）在x轴上是否存在点P，使得PAE是直角三角形？若存在这样的点P，请求出点P的坐标；若不存在，请说明理由31.已知一次函数与x轴、y轴的交点分别为A、B，试在x轴上找一点P，使PAB为等腰三角形。32.如图，在RtABC中，B = 90，AC = 60cm，A = 60，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其
9、中一个点到达终点时，另一个点也随之停止运动设点D，E运动的时间是t秒(0 y2时，即4x+4002x+820.解得x210.即当运输路程x210千米时，选择火车运输较好.；当y1y2时，即4x+4002x+820.解得x210.即当运输路程x210千米时，选择邮车运输较好25.如图，已知直线经过点A（-1，0）与点B（2，3），另一条直线经过点 B，且与x轴相交于点P（m，0） （1）求直线的解析式 （2）若APB的面积为3，求m的值（提示：分两种情形，即点P在A的左侧和右侧）参考答案:（1）设直线L1的解析式为y=kx+b，直线L1经过点A（-1，0）与点B（2，3），解得所以直线L1的解析
10、式为y=x+1（2）当点P在点A的右侧时，AP=m-（-1）=m+1，有解得：m=1此时点P的坐标为（1，0）当点P在点A的左侧时，AP=-1-m，有此时，点P的坐标为（-3，0）综上所述，m的值为1或-326.已知：如图，在梯形ABCD中，ADBC，AD=24cm，BC=30cm，点P自点A向D以1cm/s的速度运动，到D点即停止点Q自点C向B以2cm/s的速度运动，到B点即停止，直线PQ截梯形为两个四边形问当P，Q同时出发，几秒后其中一个四边形为平行四边形？参考答案:解：ADBC设运动的时间为t秒，则若AP=BQ，则此时四边形ABQP是平行四边形此时，t=30-2t解得t=10若PD=QC
11、，此时四边形ABQP是平行四边形此时，24-t=2t解得t=8综上，当t=10或t=8时四边形ABQP是平行四边形27.某景区的三个景点A，B，C在同一线路上，甲、乙两名游客从景点A出发，甲步行到景点C，乙乘景区观光车先到景点B，在B处停留一段时间后，再步行到景点C 甲、乙两人离开景点A后的路程S（米）关于时间t（分钟）的函数图象如图所示则乙出发后多长时间与甲相遇？参考答案:甲的路程S（米）与时间t（分钟）的函数关系式为： (0t90)乙的路程S（米）与时间t（分钟）的函数关系式A到B为： (20t30)由解得：t25 (分钟)还有当甲到达B地时，乙还在B地，所以由解得：t50 (分钟)答：乙
12、出发后5分钟和30分钟都与甲相遇28.已知一个等腰三角形的两角分别为(2x2)，(3x5)，求这个等腰三角形各角的度数参考答案:解：当(2x2)作为顶角时，即(2x2)2(3x5)180，解得x24，三角形三个角的度数分别为46，67，67；当(3x5)为顶角时，即(3x5)2(2x2)180，解得x27，三角形三个角的度数分别为52，52，76；当以上两个角均为底角时，即2x23x5，解得x3，三角形三个内角分别为4，4，172.29.如图，已知ABBD，CDBD。若AB=9，CD=4，BD=10，判断在BD上是否存在点P，使以P，A，B三点为顶点的三角形与以点P，C，D三点为顶点的三角形相
13、似？若存在，求BP的长；若不存在，请说明理由。参考答案:解：设BP=x时，他们相似。若ABPPDC，则,即整理得，无解。若ABPCPD，则,即，得综上，当时，两个三角形相似。30.如图，已知直线与轴交于点A，与x轴交于点D，抛物线与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为 (1，0)（1）求该抛物线的解析式；（2）在x轴上是否存在点P，使得PAE是直角三角形？若存在这样的点P，请求出点P的坐标；若不存在，请说明理由参考答案:解：（1）先求得A(0，1)，D(-2，0).把A(0，1)，B(1，0)代入可解得（2）联立方程组：，解得 所以，点E坐标为：E(4，3)假设存在这样的点使
14、得PAE是直角三角形，则若，即，解得，此时点P为 若，即，解得，此时点P为若，即，解得，此时点P为或综上，一共有4个这样的点P，它们分别是、31.已知一次函数与x轴、y轴的交点分别为A、B，试在x轴上找一点P，使PAB为等腰三角形。参考答案:解：由可得交点分别为，设点P的坐标为P(x，0)，则， 则， 分三种情况讨论PAB为等腰三角形，如图所示若BP=BA，则，即，得所以（与A重合，舍去）或若PA=PB，则，即，得所以若AP=AB，则，即，得所以或综上，存在四个点P使得PAB为等腰三角形，他们分别是，32.如图，在RtABC中，B = 90，AC = 60cm，A = 60，点D从点C出发沿C
15、A方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动设点D，E运动的时间是t秒(0 t 15)过点D作DFBC于点F，连接DE，EF(1)求证：AE = DF；(2)当t为何值时，DEF为直角三角形？请说明理由参考答案:解：(1)在DFC中，DFC = 90，C = 30，DC = 4t，DF = 2t，又AE = 2t，AE = DF(2)当DEF = 90时，由(2)知EF / AD，ADE =DEF = 90，A = 60，AD = AEcos60 = t，又AD = 60 - 4t，即60
16、- 4t = t，解得t = 12秒当EDF = 90时，四边形EBFD为矩形，在RtAED中，A = 60，则ADE = 30，AD = 2AE，即60 - 4t = 4t，解得t =秒若EFD = 90，则E与B重合，D与A重合，此种情况不存在，所以当t =秒或12秒时，DEF为直角三角形33.一次数学课上，老师请同学们在一张长为18厘米，宽为16厘米的矩形纸板上，剪下一个腰长为10厘米的等腰三角形，且要求等腰三角形的一个顶点与矩形的一个顶点重合，其它两个顶点在矩形的边上，则剪下的等腰三角形的面积为多少平方厘米？参考答案:C解答：解：如图四边形ABCD是矩形，AD18cm，AB16cm；本题可分三种情况：如图（1）：AEF中，AEAF10cm；SAEFAEAF50cm2；如图（2）：AGH中，AGGH10cm；在RtBGH中，BGABAG16106cm；根据勾股定理有：BH8cm；SAGHAGBH81040cm2；如图（3）：AMN中，AMMN10cm；在RtDMN中，MDADAM18108cm；根据勾股定理有DN6cm；SAMNAMDN10630cm2
