1、2018-2019学年山东省临沂市平邑县八年级（下）期中数学试卷一、选择题（本题共12小题每小题3分，共36分）1（3分）若二次根式有意义，则a的取值范围是（）Aa2Ba2Ca2Da22（3分）下列二次根式中，属于最简二次根式的是（）ABCD3（3分）下列计算正确的是（）ABCD24（3分）正方形具有而菱形不一定具有的性质是（）A四个角为直角B对角线互相垂直C对角线互相平分D对边平行且相等5（3分）以下各组数据为三角形的三边长，能构成直角三角形的是（）AB2，3，4C2，2，1D4，5，66（3分）如图所示，在数轴上点A所表示的数为a，则a的值为（）A1B1CD1+7（3分）如图，在RtABC
2、中，ACB90，以点A为圆心，AC长为半径作圆弧交边AB于点D若 AC3，BC4则BD的长是（）A2B3C4D58（3分）如图，在ABCD中，已知AD5cm，AB3cm，AE平分BAD交BC边于点E，则EC等于（）A1 cmB2 cmC3 cmD4 cm9（3分）如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF3，则菱形ABCD的周长是（）A12B16C20D2410（3分）如图，在矩形ABCD中，AB8，BC4，将矩形沿AC折叠，点D落在点D处，则重叠部分AFC的面积为（）A6B8C10D1211（3分）如图，在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形
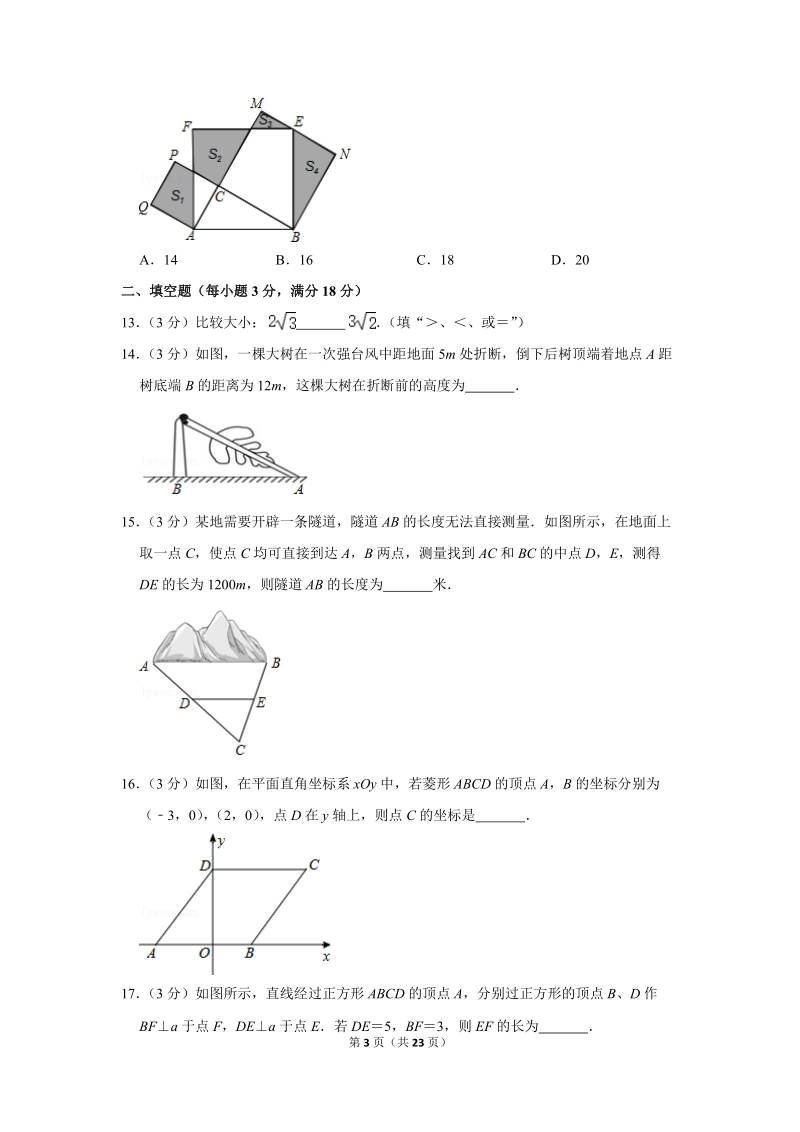
3、纸片，则图中空白部分的面积为（）cm2A168B12+8C84D4212（3分）如图，RtABC中，C90，AC3，BC4分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN，四块阴影部分的面积分别为S1、S2、S3、S4则S1+S2+S3+S4等于（）A14B16C18D20二、填空题（每小题3分，满分18分）13（3分）比较大小： （填“、或”）14（3分）如图，一棵大树在一次强台风中距地面5m处折断，倒下后树顶端着地点A距树底端B的距离为12m，这棵大树在折断前的高度为 15（3分）某地需要开辟一条隧道，隧道AB的长度无法直接测量如图所示，在地面上取一点C，使点C均
4、可直接到达A，B两点，测量找到AC和BC的中点D，E，测得DE的长为1200m，则隧道AB的长度为 米16（3分）如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A，B的坐标分别为（3，0），（2，0），点D在y轴上，则点C的坐标是 17（3分）如图所示，直线经过正方形ABCD的顶点A，分别过正方形的顶点B、D作BFa于点F，DEa于点E若DE5，BF3，则EF的长为 18（3分）观察下列各式：；，请用含n（n1）的式子写出你猜想的规律： 三、解答题（满分66分）19（10分）计算（1）（2）20（6分）如图，平行四边形ABCD的对角线AC，BD相交于点O，EF过点O且与AB、CD分别交于
5、点E、F求证：OEOF21（8分）如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点（1）在图中，以格点为端点，画线段MN；（2）在图中，以格点为顶点，画正方形ABCD，使它的面积为1022（14分）在RtABC中，BAC90，D是BC的中点，E是AD的中点，过点A作AFBC交BE的延长线于点F（1）求证：AEFDEB；（2）证明四边形ADCF是菱形；（3）若AC4，AB5，求菱形ADCF的面积23（14分）如图，在ABC中，点O是AC边上一动点，过点O作BC的平行线交ACB的角平分线于点E，交ACB的外角平分线于点F（1）求证：EOFO；（2）当点O运动到何处时，四边形C
6、EAF是矩形？请证明你的结论（3）在第（2）问的结论下，若AE3，EC4，AB12，BC13，请直接写出凹四边形ABCE的面积为 24（14分）【问题情境】如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分DAM求证：AMAD+MC【探究展示】（2）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，试判断AMAD+MC是否成立？若成立，请给出证明，若不成立，请说明理由；【拓展延伸】（3）若（2）中矩形ABCD两边AB6，BC9，求AM的长2018-2019学年山东省临沂市平邑县八年级（下）期中数学试卷参考答案与试题解析一、选择题（本题共12小题每小题3分，
7、共36分）1（3分）若二次根式有意义，则a的取值范围是（）Aa2Ba2Ca2Da2【分析】根据负数没有平方根列出关于a的不等式，求出不等式的解集确定出a的范围即可【解答】解：二次根式有意义，a20，即a2，则a的范围是a2，故选：A【点评】此题考查了二次根式有意义的条件，二次根式性质为：二次根式中的被开方数必须是非负数，否则二次根式无意义2（3分）下列二次根式中，属于最简二次根式的是（）ABCD【分析】判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是【解答】解：A、被开方数含分母，故A错误；B、被开方数含分母，故B
8、错误；C、被开方数含能开得尽方的因数，故C错误；D、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故D正确；故选：D【点评】本题考查最简二次根式的定义，被开方数不含分母；被开方数不含能开得尽方的因数或因式3（3分）下列计算正确的是（）ABCD2【分析】根据二次根式的加减法对A、C、D进行判断；根据二次根式的乘法法则对C进行判断【解答】解：A、原式2，所以A选项的计算错误；B、原式3，所以C选项的计算错误；C、原式2，所以C选项的计算正确；D、2与不能合并，所以D选项的计算错误故选：C【点评】本题考查了二次根式的混合运算：先把各二次根式化简为最简二次根式，然后进行二次根式的乘除运算，再合
9、并即可在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍4（3分）正方形具有而菱形不一定具有的性质是（）A四个角为直角B对角线互相垂直C对角线互相平分D对边平行且相等【分析】举出正方形具有而菱形不一定具有的所有性质，即可得出答案【解答】解：正方形具有而菱形不一定具有的性质是：正方形的对角线相等，而菱形不一定对角线相等，正方形的四个角是直角，而菱形的四个角不一定是直角，故选：A【点评】本题考查了对正方形、菱形的性质的应用，主要根据学生的理解能力和辨析能力解答5（3分）以下各组数据为三角形的三边长，能构成直角三角形的是（）AB2，3，4C2，2，1
10、D4，5，6【分析】由（2）2+（2）21642，可得出三边长为2，2，4的三角形为直角三角形，此题得解【解答】解：（2）2+（2）21642，三边长为2，2，4的三角形为直角三角形故选：A【点评】本题考查了勾股定理的逆定理，牢记“如果三角形的三边长a，b，c满足a2+b2c2，那么这个三角形就是直角三角形”是解题的关键6（3分）如图所示，在数轴上点A所表示的数为a，则a的值为（）A1B1CD1+【分析】点A在以O为圆心，OB长为半径的圆上，所以在直角BOC中，根据勾股定理求得圆O的半径OAOB，然后由实数与数轴的关系可以求得a的值【解答】解：如图，点A在以O为圆心，OB长为半径的圆上在直角B
11、OC中，OC2，BC1，则根据勾股定理知OB，OAOB，a1故选：A【点评】本题考查了勾股定理、实数与数轴找出OAOB是解题的关键7（3分）如图，在RtABC中，ACB90，以点A为圆心，AC长为半径作圆弧交边AB于点D若 AC3，BC4则BD的长是（）A2B3C4D5【分析】首先利用勾股定理可以算出AB的长，再根据题意可得到ADAC，根据BDABAD即可算出答案【解答】解：AC3，BC4，AB5，以点A为圆心，AC长为半径画弧，交AB于点D，ADAC，AD3，BDABAD532故选：A【点评】此题主要考查了勾股定理，关键是熟练掌握勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等
12、于斜边长的平方8（3分）如图，在ABCD中，已知AD5cm，AB3cm，AE平分BAD交BC边于点E，则EC等于（）A1 cmB2 cmC3 cmD4 cm【分析】根据平行四边形的性质和角平分线的性质可以推导出等角，进而得到等腰三角形，推得ABBE，根据AD、AB的值，求出EC的长【解答】解：ADBC，DAEBEA，AE平分BAD，BAEDAE，BAEBEA，BEAB3cm，BCAD5cm，ECBCBE532cm，故选：B【点评】本题主要考查了平行四边形的性质，等腰三角形的判定；在平行四边形中，当出现角平分线时，一般可构造等腰三角形，进而利用等腰三角形的性质解题9（3分）如图，菱形ABCD中，
13、E、F分别是AB、AC的中点，若EF3，则菱形ABCD的周长是（）A12B16C20D24【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出BC，再根据菱形的周长公式列式计算即可得解【解答】解：E、F分别是AB、AC的中点，EF是ABC的中位线，BC2EF236，菱形ABCD的周长4BC4624故选：D【点评】本题主要考查了菱形的四条边都相等，三角形的中位线平行于第三边并且等于第三边的一半，求出菱形的边长是解题的关键10（3分）如图，在矩形ABCD中，AB8，BC4，将矩形沿AC折叠，点D落在点D处，则重叠部分AFC的面积为（）A6B8C10D12【分析】因为BC为AF边上的高，要
14、求AFC的面积，求得AF即可，求证AFDCFB，得BFDF，设DFx，则在RtAFD中，根据勾股定理求x，于是得到AFABBF，即可得到结果【解答】解：易证AFDCFB，DFBF，设DFx，则AF8x，在RtAFD中，（8x）2x2+42，解之得：x3，AFABFB835，SAFCAFBC10故选：C【点评】本题考查了翻折变换折叠问题，勾股定理的正确运用，本题中设DFx，根据直角三角形AFD中运用勾股定理求x是解题的关键11（3分）如图，在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片，则图中空白部分的面积为（）cm2A168B12+8C84D42【分析】根据正方形
15、的面积求出两个正方形的边长，从而求出AB、BC，再根据空白部分的面积等于长方形的面积减去两个正方形的面积列式计算即可得解【解答】解：两张正方形纸片的面积分别为16cm2和12cm2，它们的边长分别为4cm，2cm，AB4cm，BC（2+4）cm，空白部分的面积（2+4）41216，8+161216，（12+8）cm2故选：B【点评】本题考查了二次根式的应用，算术平方根的定义，解题的关键在于根据正方形的面积求出两个正方形的边长12（3分）如图，RtABC中，C90，AC3，BC4分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN，四块阴影部分的面积分别为S1、S2、S3、
16、S4则S1+S2+S3+S4等于（）A14B16C18D20【分析】过F作AM的垂线交AM于D，通过证明S1+S2+S3+S4RtABC的面积3，依此即可求解【解答】解：过F作AM的垂线交AM于D，可证明RtADFRtABC，RtDFKRtCAT，所以S2SRtABC由RtDFKRtCAT可进一步证得：RtFPTRtEMK，S3SFPT，又可证得RtAQFRtACB，S1+S3SRtAQFSRtABC易证RtABCRtEBN，S4SRtABC，S1+S2+S3+S4（S1+S3）+S2+S4SRtABC+SRtABC+SRtABCSRtABC3432318故选：C【点评】本题考查勾股定理的知识
17、，有一定难度，解题关键是将勾股定理和正方形的面积公式进行灵活的结合和应用二、填空题（每小题3分，满分18分）13（3分）比较大小：（填“、或”）【分析】先把两个实数平方，然后根据实数的大小比较方法即可求解【解答】解：（）212，（3）218，而1218，23故答案为：【点评】此题主要考查了实数的大小的比较，比较两个实数的大小，可以采用作差法、取近似值法、比较n次方的方法等14（3分）如图，一棵大树在一次强台风中距地面5m处折断，倒下后树顶端着地点A距树底端B的距离为12m，这棵大树在折断前的高度为18m【分析】根据大树的折断部分与未断部分、地面恰好构成直角三角形，再根据勾股定理求出AC的长，进
18、而可得出结论【解答】解：树的折断部分与未断部分、地面恰好构成直角三角形，且BC5m，AB12m，AC13（m），这棵树原来的高度BC+AC5+1318（m）答：棵树原来高18m故答案为：18米【点评】本题考查的是勾股定理的应用，熟知直角三角形斜边的平方等于两直角边的平方和是解答此题的关键15（3分）某地需要开辟一条隧道，隧道AB的长度无法直接测量如图所示，在地面上取一点C，使点C均可直接到达A，B两点，测量找到AC和BC的中点D，E，测得DE的长为1200m，则隧道AB的长度为2400米【分析】由D为AC的中点、E为BC的中点，可得出DE为ABC的中位线，根据DE的长度结合三角形中位线定理即可
19、得出AB的长度【解答】解：D为AC的中点，E为BC的中点，DE为ABC的中位线，又DE1200m，AB2DE2400m故答案是：2400【点评】本题考查了三角形中位线定理，根据DE的长度结合三角形中位线定理求出AB的长是解题的关键16（3分）如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A，B的坐标分别为（3，0），（2，0），点D在y轴上，则点C的坐标是（5，4）【分析】利用菱形的性质以及勾股定理得出DO的长，进而求出C点坐标【解答】解：菱形ABCD的顶点A，B的坐标分别为（3，0），（2，0），点D在y轴上，AB5，DO4，点C的坐标是：（5，4）故答案为：（5，4）【点评】此题主要
20、考查了菱形的性质以及坐标与图形的性质，得出DO的长是解题关键17（3分）如图所示，直线经过正方形ABCD的顶点A，分别过正方形的顶点B、D作BFa于点F，DEa于点E若DE5，BF3，则EF的长为8【分析】首先证明ABFEAD，再利用AAS定理证明AFBDEA，进而得到AFED5，AEBF3，然后再根据线段的和差关系可得答案【解答】解：四边形ABCD是正方形，BAD90，ABAD，BAF+EAD90，BFa，DEa，AEDAFB90BAF+ABF90，ABFEAD，AFBDEA，AFED5，AEBF3，EFAF+AE5+38，故答案为：8【点评】本题考查了正方形性质，全等三角形的性质和判定的应
21、用，关键是推出AFBDEA18（3分）观察下列各式：；，请用含n（n1）的式子写出你猜想的规律：（n+1）【分析】从给出的三个式子中，我们可以发现计算出的等号后面的系数为等号前面的根号里的整数加分数的分子，根号里的还是原来的分数，依此可以找出规律【解答】解：从三个式子中，我们可以发现计算出的等号后面的系数为等号前面的根号里的整数加分数的分子，根号里的还是原来的分数，即（n+1）【点评】做这类题的关键是仔细观察各式从中找出规律三、解答题（满分66分）19（10分）计算（1）（2）【分析】（1）先根据二次根式的乘除法则运算，然后化简后合并即可；（2）先根据二次根式的除法法则和完全平方公式运算，然后
22、合并即可【解答】解：（1）原式6+6+5；（2）原式2+12+32+424【点评】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍20（6分）如图，平行四边形ABCD的对角线AC，BD相交于点O，EF过点O且与AB、CD分别交于点E、F求证：OEOF【分析】由平行四边形性质可证得AOECOF，则可证得OEOF【解答】证明：四边形ABCD为平行四边形，ABCD，OAOC，EAOFCO，在AOE和COF中AOECOF（ASA），OEOF【点评】本题主
23、要考查平行四边形的性质，掌握平行四边形的对边平行、对角线互相平分是解题的关键21（8分）如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点（1）在图中，以格点为端点，画线段MN；（2）在图中，以格点为顶点，画正方形ABCD，使它的面积为10【分析】（1）以3和2为直角边作出直角三角形，斜边即为所求；（2）以3和1为直角边作出直角三角形，斜边为正方形的边长，如图所示【解答】解：（1）如图所示：（2）如图所示【点评】此题考查了勾股定理，熟练掌握勾股定理是解本题的关键22（14分）在RtABC中，BAC90，D是BC的中点，E是AD的中点，过点A作AFBC交BE的延长线于点F（1
24、）求证：AEFDEB；（2）证明四边形ADCF是菱形；（3）若AC4，AB5，求菱形ADCF的面积【分析】（1）利用平行线的性质及中点的定义，可利用AAS证得结论；（2）由（1）可得AFBD，结合条件可求得AFDC，则可证明四边形ADCF为平行四边形，再利用直角三角形的性质可证得ADCD，可证得四边形ADCF为菱形；（3）连接DF，可证得四边形ABDF为平行四边形，则可求得DF的长，利用菱形的面积公式可求得答案【解答】（1）证明：AFBC，AFEDBE，E是AD的中点，AEDE，在AFE和DBE中，AFEDBE（AAS）；（2）证明：由（1）知，AFEDBE，则AFDBAD为BC边上的中线DB
25、DC，AFCDAFBC，四边形ADCF是平行四边形，BAC90，D是BC的中点，E是AD的中点，ADDCBC，四边形ADCF是菱形；（3）连接DF，AFBD，AFBD，四边形ABDF是平行四边形，DFAB5，四边形ADCF是菱形，S菱形ADCFACDF4510【点评】本题主要考查菱形的性质及判定，利用全等三角形的性质证得AFCD是解题的关键，注意菱形面积公式的应用23（14分）如图，在ABC中，点O是AC边上一动点，过点O作BC的平行线交ACB的角平分线于点E，交ACB的外角平分线于点F（1）求证：EOFO；（2）当点O运动到何处时，四边形CEAF是矩形？请证明你的结论（3）在第（2）问的结论
26、下，若AE3，EC4，AB12，BC13，请直接写出凹四边形ABCE的面积为24【分析】（1）由平行线的性质和角平分线的定义得出OECOCE，证出EOCO，同理得出FOCO，即可得出EOFO；（2）由对角线互相平分证明四边形CEAF是平行四边形，再由对角线相等即可得出结论；（3）先根据勾股定理求出AC，得出ACE的面积AEEC，再由勾股定理的逆定理证明ABC是直角三角形，得出ABC的面积ABAC，凹四边形ABCE的面积ABC的面积ACE的面积，即可得出结果【解答】（1）证明：EFBC，OECBCE，CE平分ACB，BCEOCE，OECOCE，EOCO，同理：FOCO，EOFO；（2）解：当点O
27、运动到AC的中点时，四边形CEAF是矩形；理由如下：由（1）得：EOFO，又O是AC的中点，AOCO，四边形CEAF是平行四边形，EOFOCO，EOFOAOCO，EFAC，四边形CEAF是矩形；（3）解：由（2）得：四边形CEAF是矩形，AEC90，AC5，ACE的面积AEEC346，122+52132，即AB2+AC2BC2，ABC是直角三角形，BAC90，ABC的面积ABAC12530，凹四边形ABCE的面积ABC的面积ACE的面积30624；故答案为：24【点评】本题考查了矩形的判定与性质、平行线的性质、角平分线、等腰三角形的判定、勾股定理以及面积的计算；熟练掌握矩形的判定与性质，并能进
28、行推理论证与计算是解决问题的关键24（14分）【问题情境】如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分DAM求证：AMAD+MC【探究展示】（2）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，试判断AMAD+MC是否成立？若成立，请给出证明，若不成立，请说明理由；【拓展延伸】（3）若（2）中矩形ABCD两边AB6，BC9，求AM的长【分析】（1）先构造出ADENCE，即可得出结论；（2）同（1）的方法即可得出结论；（3）设出MCx，利用（2）的结论得出AM9+x，再利用勾股定理建立方程求出CM即可得出结论【解答】解：（1）如图1，延长AE，BC相
29、交于N，四边形ABCD是正方形，ADBC，DAEENC，AE平分DAE，DAEMAE，ENCMAE，在ADE和NCE中，ADENCE，ADCN，AMMNNC+MCAD+MC；（2）结论AMAD+CM仍然成立，理由：如图2，延长AE，BC相交于N，四边形ABCD是矩形，ADBC，DAEENC，AE平分DAE，DAEMAE，ENCMAE，在ADE和NCE中，ADENCE，ADCN，AMMNNC+MCAD+MC；（3）设MCx，则BMBCCN9x，由（2）知，AMAD+MC9+x，在RtABM中，AM2BM2AB2，（9+x）2（9x）236，x1，AMAD+MC10【点评】此题是四边形综合题，主要考查了正方形的性质，矩形的性质，全等三角形的判定和性质，勾股定理，解本题的关键是判断出ADENCE和利用勾股定理建立方程，是一道基础题目
