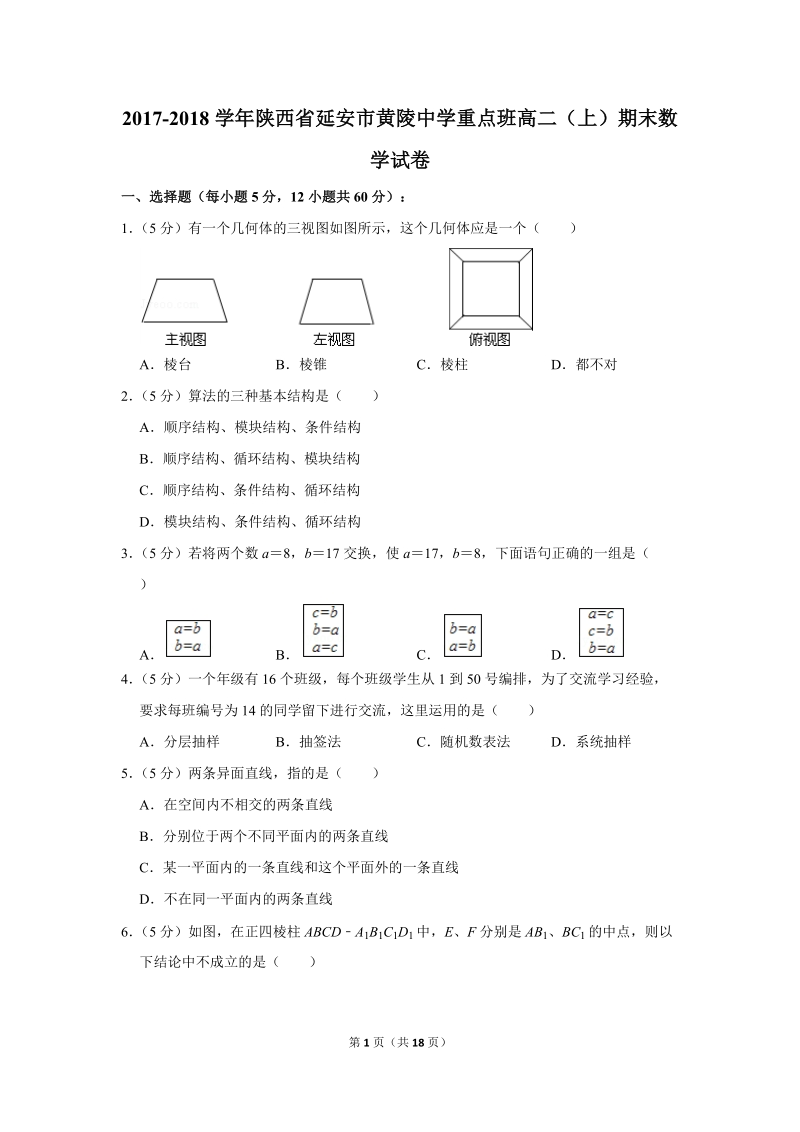
1、2017-2018学年陕西省延安市黄陵县二校联考重点班高二（上）期末数学试卷一、选择题（每小题5分，12小题共60分）：1（5分）有一个几何体的三视图如图所示，这个几何体应是一个（）A棱台B棱锥C棱柱D都不对2（5分）算法的三种基本结构是（）A顺序结构、模块结构、条件结构B顺序结构、循环结构、模块结构C顺序结构、条件结构、循环结构D模块结构、条件结构、循环结构3（5分）若将两个数a8，b17交换，使a17，b8，下面语句正确的一组是（）ABCD4（5分）一个年级有16个班级，每个班级学生从1到50号编排，为了交流学习经验，要求每班编号为14的同学留下进行交流，这里运用的是（）A分层抽样B抽签法
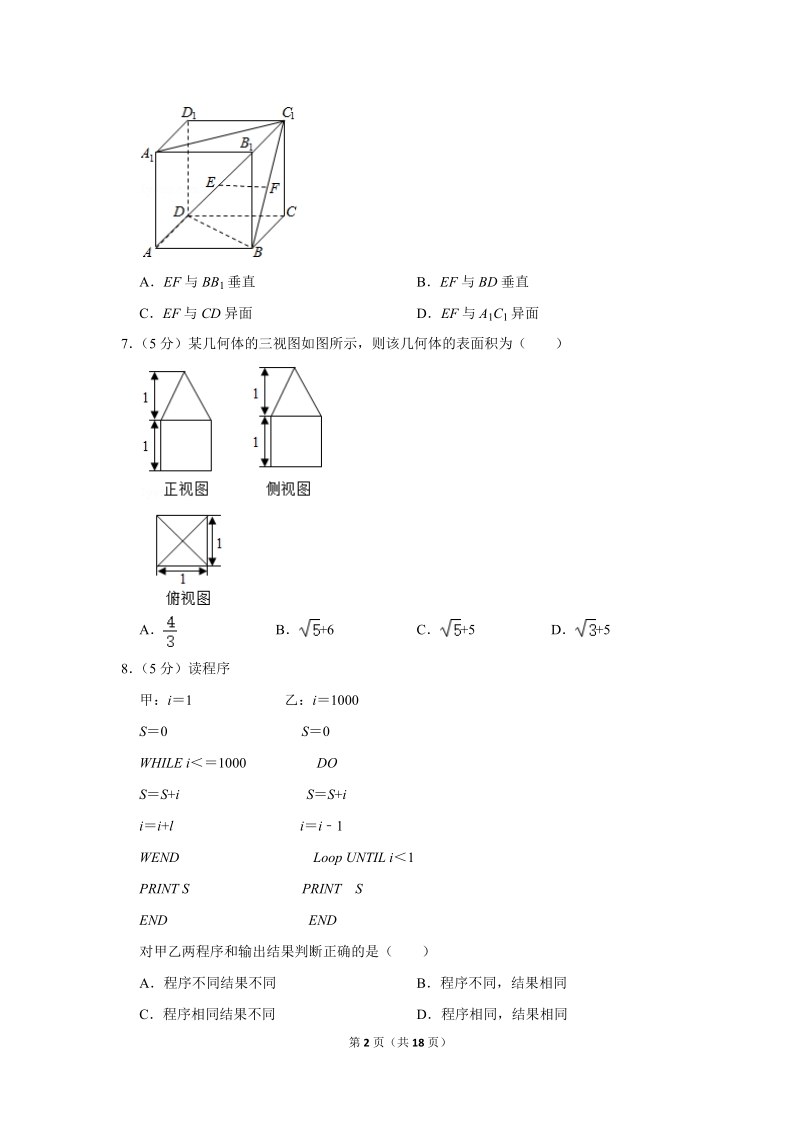
2、C随机数表法D系统抽样5（5分）两条异面直线，指的是（）A在空间内不相交的两条直线B分别位于两个不同平面内的两条直线C某一平面内的一条直线和这个平面外的一条直线D不在同一平面内的两条直线6（5分）如图，在正四棱柱ABCDA1B1C1D1中，E、F分别是AB1、BC1的中点，则以下结论中不成立的是（）AEF与BB1垂直BEF与BD垂直CEF与CD异面DEF与A1C1异面7（5分）某几何体的三视图如图所示，则该几何体的表面积为（）AB+6C+5D+58（5分）读程序甲：i1 乙：i1000S0 S0WHILE i1000 DOSS+i SS+iii+l ii1WEND Loop UNTIL i1P
3、RINT S PRINT SEND END对甲乙两程序和输出结果判断正确的是（）A程序不同结果不同B程序不同，结果相同C程序相同结果不同D程序相同，结果相同9（5分）某篮球运动员在一个赛季的40场比赛中的得分的茎叶图如图所示：则中位数与众数分别为（）A3与3B23与3C3与23D23与2310（5分）如果事件A与B是互斥事件，则（）AAB是必然事件B与一定是互斥事件C与一定不是互斥事件D是必然事件11（5分）已知点P是边长为4的正方形内任一点，则P到四个顶点的距离均大于2的概率是（）ABCD12（5分）为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁18岁的男生体重（
4、kg），得到频率分布直方图如图根据图可得这100名学生中体重在56.5，64.5的学生人数是（）A20B30C40D50二、填空题（每小题5分，共20分）13（5分）若1，则f（x0）等于 14（5分）甲校有3600名学生，乙校有5400名学生，丙校有1800名学生为统计三校学生某方面的情况，计划采用分层抽样法，抽取一个样本容量为90人的样本，则应在甲校抽取的学生数是 15（5分）已知x、y之间的一组数据如下：x0123y8264则线性回归方程所表示的直线必经过点 16（5分）已知f（x）（x1）（x2）（x3）（x4）（x5），则f（1） 三、解答题（5小题共70分）17（10分）从甲、乙两
5、名学生中选拔一人参加射箭比赛，为此需要对他们的射箭水平进行测试现这两名学生在相同条件下各射箭10次，命中的环数如下：甲897976101086乙10986879788（1）计算甲、乙两人射箭命中环数的平均数和标准差；（2）比较两个人的成绩，然后决定选择哪名学生参加射箭比赛18（15分）从含有两件正品a，b和一件次品c的3件产品中每次任取一件，连续取两次，求取出的两件产品中恰有一件是次品的概率（1）每次取出不放回；（2）每次取出后放回19（15分）某射击运动员射击1次，命中10环、9环、8环、7环的概率分别为0.20，0.22，0.25，0.28计算该运动员在1次射击中：（1）至少命中7环的概率
6、；（2）命中不足8环的概率20（15分）假设关于某设备的使用年限x和所支出的维修费用y（万元），有如下的统计数据（xi，yi）（i1，2，3，4，5）由资料知y对x呈线性相关，并且统计的五组数据得平均值分别为，若用五组数据得到的线性回归方程bx+a去估计，使用8年的维修费用比使用7年的维修费用多1.1万元，（1）求回归直线方程；（2）估计使用年限为10年时，维修费用是多少？21（15分）设计算法流程图，要求输入自变量x的值，输出函数f（x）的值，并用复合if语句描述算法2017-2018学年陕西省延安市黄陵县二校联考重点班高二（上）期末数学试卷参考答案与试题解析一、选择题（每小题5分，12小题
7、共60分）：1（5分）有一个几何体的三视图如图所示，这个几何体应是一个（）A棱台B棱锥C棱柱D都不对【分析】根据主视图、左视图、俯视图的形状，将它们相交得到几何体的形状【解答】解：由三视图知，从正面和侧面看都是梯形，从上面看为正方形，下面看是正方形，并且可以想象到连接相应顶点的四条线段就是几何体的四条侧棱，故这个三视图是四棱台 故选A【点评】本题考查几何体的三视图与直观图之间的相互转化2（5分）算法的三种基本结构是（）A顺序结构、模块结构、条件结构B顺序结构、循环结构、模块结构C顺序结构、条件结构、循环结构D模块结构、条件结构、循环结构【分析】本题是概念型题，算法的三种基本结构是顺序结构、条件
8、结构、循环结构，由此对比四个选项得出正确选项即可【解答】解：算法的三种基本结构是顺序结构、条件结构、循环结构，故选：C【点评】本题考查程序框图的三种基本逻辑结构的概念，求解本题的关键是对算法的三种基本结构的了解3（5分）若将两个数a8，b17交换，使a17，b8，下面语句正确的一组是（）ABCD【分析】要实现两个变量a，b值的交换，需要借助中间量c，先把b的值赋给中间变量c，再把a的值赋给变量b，把c的值赋给变量a【解答】解：先把b的值赋给中间变量c，这样c17，再把a的值赋给变量b，这样b8，把c的值赋给变量a，这样a17故选：B【点评】本题考查的是赋值语句，考查逻辑思维能力，属于基础题4（
9、5分）一个年级有16个班级，每个班级学生从1到50号编排，为了交流学习经验，要求每班编号为14的同学留下进行交流，这里运用的是（）A分层抽样B抽签法C随机数表法D系统抽样【分析】学生人数比较多，把每个班级学生从1到50号编排，要求每班编号为14的同学留下进行交流，这样选出的样本是具有相同的间隔的样本，是采用系统抽样的方法【解答】解：学生人数比较多，把每个班级学生从1到50号编排，要求每班编号为14的同学留下进行交流，这样选出的样本是采用系统抽样的方法，故选：D【点评】本题考查系统抽样，当总体容量N较大时，采用系统抽样，将总体分成均衡的若干部分即将总体分段，分段的间隔要求相等，系统抽样又称等距抽
10、样5（5分）两条异面直线，指的是（）A在空间内不相交的两条直线B分别位于两个不同平面内的两条直线C某一平面内的一条直线和这个平面外的一条直线D不在同一平面内的两条直线【分析】直接由异面直线的定义，判断选项的正误即可【解答】解：A两条直线可能平行，所以不正确B分别位于两个不同平面内的两条直线，可能还在另一个平面，不正确C某一平面内的一条直线和这个平面外的一条直线可能在同一个平面，不正确D是异面直线的定义，正确【点评】本题考查异面直线的定义，是基础题6（5分）如图，在正四棱柱ABCDA1B1C1D1中，E、F分别是AB1、BC1的中点，则以下结论中不成立的是（）AEF与BB1垂直BEF与BD垂直C
11、EF与CD异面DEF与A1C1异面【分析】观察正方体的图形，连B1C，则B1C交BC1于F且F为BC1中点，推出EFA1C1；分析可得答案【解答】解：连B1C，则B1C交BC1于F且F为BC1中点，三角形B1AC中EF，所以EF平面ABCD，而B1B面ABCD，所以EF与BB1垂直；又ACBD，所以EF与BD垂直，EF与CD异面由EF，ACA1C1得EFA1C1故选：D【点评】本题考查异面直线的判定，考查空间想象能力，是基础题7（5分）某几何体的三视图如图所示，则该几何体的表面积为（）AB+6C+5D+5【分析】三视图复原的组合体是下部是正方体，上部是四棱锥，根据三视图数据，求出表面积即可【解
12、答】解：三视图复原的组合体是下部是棱长为1的正方体，上部是底面边长为1的正方形，高为1的四棱锥，组合体的表面积为：511+41+5，故选：C【点评】本题考查由三视图求表面积，考查计算能力，空间想象能力，是基础题8（5分）读程序甲：i1 乙：i1000S0 S0WHILE i1000 DOSS+i SS+iii+l ii1WEND Loop UNTIL i1PRINT S PRINT SEND END对甲乙两程序和输出结果判断正确的是（）A程序不同结果不同B程序不同，结果相同C程序相同结果不同D程序相同，结果相同【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是
13、利用循环计算并打印S值【解答】解：程序甲是计数变量i从1开始逐步递增直到i1000时终止，累加变量从0开始，这个程序计算的是：1+2+3+1000；程序乙计数变量从1000开始逐步递减到i1时终止，累加变量从0开始，这个程序计算的是1000+999+1但这两个程序是不同的两种程序的输出结果都是：S1+2+3+1000100500故选：B【点评】考查由框图分析出算法结构的能力，本题考查是循环的结果9（5分）某篮球运动员在一个赛季的40场比赛中的得分的茎叶图如图所示：则中位数与众数分别为（）A3与3B23与3C3与23D23与23【分析】根据所给的茎叶图，可以看出本题要用的40个数据，从茎叶图可以
14、看出，数据是按照从小到大排列的，一共有40个数字，中位数是第20与21个数字的平均数23，从这组数据可以看出23出现4次，是出现次数最多的一个数，得到结果【解答】解：根据所给的茎叶图，可以看出本题要用的40个数据，从茎叶图可以看出，数据是按照从小到大排列的，一共有40个数字，中位数是第20与21个数字的平均数23，从这组数据可以看出23出现4次，是出现次数最多的一个数，众数是23，故选：D【点评】对于一组数据，通常要求的是这组数据的众数，中位数，平均数分别表示一组数据的特征，这样的问题可以出现在选择题或填空题考查最基本的知识点10（5分）如果事件A与B是互斥事件，则（）AAB是必然事件B与一定
15、是互斥事件C与一定不是互斥事件D是必然事件【分析】由互斥事件的意义可知，我们所学的互斥事件是不能同时发生的事件，它与对立事件不同，它们的补集的和事件一定是必然事件可以用韦恩图来观察【解答】解：由互斥事件的意义可知，互斥事件是不能同时发生的事件，它与对立事件不同，它们的补集的和事件一定是必然事件，故选：D【点评】本题考查互斥事件和对立事件，分清互斥事件和对立事件之间的关系，互斥事件是不可能同时发生的事件，对立事件是指一个不发生，另一个一定发生的事件11（5分）已知点P是边长为4的正方形内任一点，则P到四个顶点的距离均大于2的概率是（）ABCD【分析】根据题意，先求出满足条件的正方形ABCD的面积
16、，再求出满足条件正方形内的点到正方形的顶点A、B、C、D的距离均不小于2的图形的面积，然后代入几何概型公式即可得到答案【解答】解：满足条件的正方形ABCD如下图所示：其中正方形的面积S正方形4416；满足到正方形的顶点A、B、C、D的距离均不小于2的平面区域如图中阴影部分所示则S阴影164，故该正方形内的点到正方形的顶点A、B、C、D的距离均不小于1的概率是P；故选：A【点评】本题考查几何概型，解题的关键理解几何概型的意义，即将长度、面积、体积的比值转化为事件发生的概率12（5分）为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁18岁的男生体重（kg），得到频率分布直
17、方图如图根据图可得这100名学生中体重在56.5，64.5的学生人数是（）A20B30C40D50【分析】由频率直方图中的小长方形的面积即为该范围内的频率，先求出体重在56.5，64.5的频率，再由样本的容量求人数【解答】解：由频率直方图得，体重在56.5，64.5的频率为0.032+0.052+0.052+0.0720.4，所求人数为1000.440故选：C【点评】频率分布直方图是高考新增的考点，难度不高，但必须掌握相关的概念二、填空题（每小题5分，共20分）13（5分）若1，则f（x0）等于【分析】根据极限的定义可以联想到将3x看做一个整体除以3再乘以3同时当x0时3x0即可得到即可得解【
18、解答】解：1故答案为：【点评】本题住考查了利用极限的定义求极限值关键是分母成以3分母乘以然后根据极限的定义即可求出f（x0）14（5分）甲校有3600名学生，乙校有5400名学生，丙校有1800名学生为统计三校学生某方面的情况，计划采用分层抽样法，抽取一个样本容量为90人的样本，则应在甲校抽取的学生数是30【分析】根据分层抽样的定义，即可确定甲校抽取的人数【解答】解：甲校，乙校，丙校的学生的人数之比为：3600：5400：18002：3：1，抽取一个样本容量为90人的样本，则应在甲校抽取的学生数为：，故答案为：30【点评】本题主要考查分层抽样的定义和应用，根据分层抽样的定义确定对应的抽取比例是
19、解决本题的关键，比较基础15（5分）已知x、y之间的一组数据如下：x0123y8264则线性回归方程所表示的直线必经过点（，5）【分析】先利用数据平均值的公式求出x，y的平均值，以平均值为横、纵坐标的点在回归直线上，即样本中心点在线性回归直线上【解答】解：，5线性回归方程ya+bx所表示的直线必经过点（1.5，5）故选C【点评】解决线性回归直线的方程，利用最小二乘法求出直线的截距和斜率，注意由公式判断出回归直线一定过样本中心点16（5分）已知f（x）（x1）（x2）（x3）（x4）（x5），则f（1）24【分析】根据导数的运算法则即可得到结论【解答】解：f（x）（x1）（x2）（x3）（x4）
20、（x5），令g（x）（x2）（x3）（x4）（x5），则f（x）（x1）g（x）f（x）（x1）g（x）+（x1）g（x）g（x）+（x1）g（x），则f（1）g（1）+（11）g（1）g（1），g（1）（12）（13）（14）（15）24，f（1）g（1）24，故答案为：24【点评】本题主要考查导数的计算，利用导数的运算法则是解决本题的关键三、解答题（5小题共70分）17（10分）从甲、乙两名学生中选拔一人参加射箭比赛，为此需要对他们的射箭水平进行测试现这两名学生在相同条件下各射箭10次，命中的环数如下：甲897976101086乙10986879788（1）计算甲、乙两人射箭命中环数的平均
21、数和标准差；（2）比较两个人的成绩，然后决定选择哪名学生参加射箭比赛【分析】1【解答】解：（1）根据题中所给数据，则甲的平均数为，乙的平均数为，甲的标准差为，乙的标准差为，故甲的平均数为8，标准差为，乙的平均数为8，标准差为；（2），且，乙的成绩较为稳定，故选择乙参加射箭比赛【点评】118（15分）从含有两件正品a，b和一件次品c的3件产品中每次任取一件，连续取两次，求取出的两件产品中恰有一件是次品的概率（1）每次取出不放回；（2）每次取出后放回【分析】（1）每次取出一个，取后不放回地连续取两次，其一切可能的结果组成的基本事件有6个，可以列举出所有的事件，从列举出的事件中看出取出的两件中，恰好
22、有一件次品的事件数，得到概率（2）根据题意用列举法解题，记两件产品中恰有一件是次品为事件A，依次列举所有的基本事件，可得其情况数目，分析可得事件A的情况数目，由等可能事件的概率公式，计算可得答案【解答】解（1）每次取出不放回的所有结果有：（a，b），（a，c），（b，a），（b，c），（c，a），（c，b），其中左边的字母表示第一次取出的产品，右边的字母表示第二次取出的产品，共有6个基本事件，其中恰有一件次品的事件有4个，所以每次取出不放回，取出的两件产品中恰有一件是次品的概率为（2）每次取出后放回的所有结果：（a，a），（a，b），（a，c），（b，a），（b，b），（b，c），（c，a），
23、（c，b），（c，c）共有9个基本事件，其中恰有一件次品的事件有4个，所以每次取出后放回，取出的两件产品中恰有一件是次品的概率为【点评】本题考查等可能事件的概率，涉及列举法的运用；注意本题是有放回抽样，共9种情况19（15分）某射击运动员射击1次，命中10环、9环、8环、7环的概率分别为0.20，0.22，0.25，0.28计算该运动员在1次射击中：（1）至少命中7环的概率；（2）命中不足8环的概率【分析】（1）由互斥事件的概率加法公式直接求解；（2）由（1）结合对立事件的概率求出命中不足7环，然后直接由互斥事件的概率加法公式求解【解答】解：记事件“射击1次，命中k环”为Ak（kN，且k10）
24、，则事件Ak彼此互斥（1）记“射击1次，至少命中7环”为事件A，那么当A10，A9，A8，A7之一发生时，事件A发生由互斥事件的概率加法公式，得P（A）P（A10+A9+A8+A7）P（A10）+P（A9）+P（A8）+P（A7）0.20+0.22+0.25+0.280.95；（2）事件“射击1次，命中不足7环”是事件“射击1次，至少命中7环”的对立事件，即表示事件“射击1次，命中不足7环”根据对立事件的概率公式，得记事件“射击1次，命中不足8环”为B，那么与A7之一发生，B发生，而与A7是互斥事件，于是答：该运动员在1次射击中，至少命中7环的概率为0.95；命中不足8环的概率为0.33【点评
25、】本题考查了互斥事件的概率加法公式，考查了对立事件的概率的求法，是基础的计算题20（15分）假设关于某设备的使用年限x和所支出的维修费用y（万元），有如下的统计数据（xi，yi）（i1，2，3，4，5）由资料知y对x呈线性相关，并且统计的五组数据得平均值分别为，若用五组数据得到的线性回归方程bx+a去估计，使用8年的维修费用比使用7年的维修费用多1.1万元，（1）求回归直线方程；（2）估计使用年限为10年时，维修费用是多少？【分析】（1）因为线性回归方程bx+a经过定点（，），将，代入回归方程得5.44b+a；利用使用8年的维修费用比使用7年的维修费用多1.1万元，可得8b+a（7b+a）1.
26、1，从而可求b，a的值，进而可得回归直线方程；（2）将x10代入线性回归方程，即得维修费用【解答】解：（1）因为线性回归方程bx+a经过定点（，），将，代入回归方程得5.44b+a； 又8b+a（7b+a）1.1解得b1.1，a1，线性回归方程1.1x+1（6分）（2）将x10代入线性回归方程得y12（万元）使用年限为10年时，维修费用是12（万元）（12分）【点评】本题以实际问题为载体，考查回归分析的初步应用，解题的关键是利用线性回归方程bx+a经过定点（，）21（15分）设计算法流程图，要求输入自变量x的值，输出函数f（x）的值，并用复合if语句描述算法【分析】根据题意设计程序框图，由已知中分段函数的解析式，根据分类标准，设置两个判断框并设置出判断框中的条件，再由函数各段的解析式，确定判断框的“是”与“否”分支对应的操作，由此画出流程图，再编写满足题意的程序语句【解答】解：根据题意，设计算法流程图如下；算法语句为：INPUT x；IF x0，THEN f（x）：/2*x+3；ELSE IF x0，THEN f（x）：0；ELSE f（x）：/2*x5PRINT f（x）【点评】本题考查了设计程序框图解决实际问题，以及编写程序解决分段函数的应用问题，是综合题
