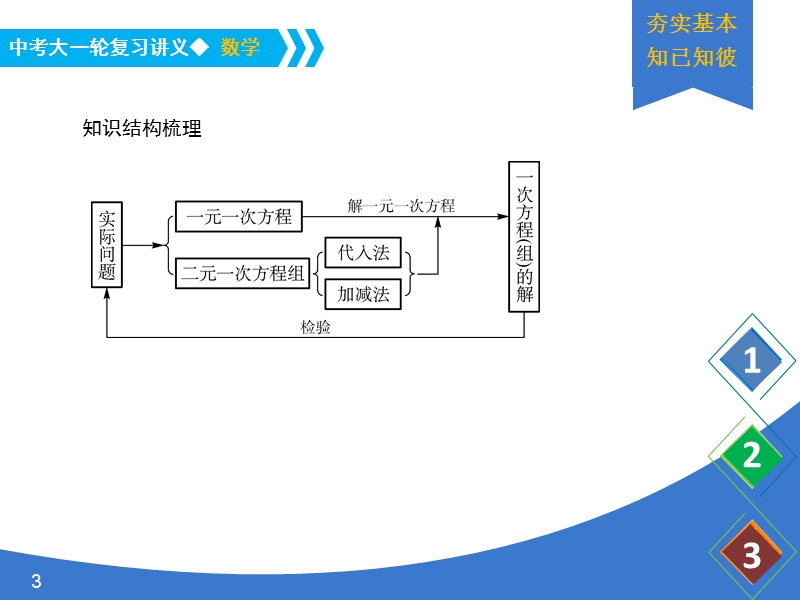
1、,课时7 一元一次方程(组)及其应用,夯实基本 知已知彼,知识结构梳理,夯实基本 知已知彼,基础知识回顾 1. 一元一次方程 (1)定义：只含有_个未知数，并且未知数的次数是_的整式方程叫做一元一次方程 (2)解一元一次方程的步骤： 去_；去_；移_；合并_；系数化为1. 温馨提示 解方程时，有些变形步骤可能用不到，并且也不一定按照自上而下的顺序，要根据方程的形式灵活安排求解步骤熟练后，步骤及检验还可以合并简化,夯实基本 知已知彼,2. 二元一次方程(组) (1)二元一次方程的定义：含有_未知数(元)，并且含未知数的项的次数是_的整式方程 (2)二元一次方程组的定义：由2个或2个以上的_组成的
2、方程组叫二元一次方程组 (3)二元一次方程组的解的定义：使二元一次方程组_，叫做二元一次方程组的解 3. 二元一次方程组的解法 解二元一次方程组的关键是消元，方法有_消元法和_消元法两种 温馨提示 利用加减法消元时，一定要注意各项系数的符号 4. 一次方程(组)的应用 列一次方程(组)的一般步骤： (1)审题(2)设_(3)找_，列出方程(4)解方程(5)检验(6)作答,课前预测你很棒,A,B,B,D,D,课前预测你很棒,热点看台 快速提升,热点一 列一次方程(组) 热点搜索 列方程(组)步骤如下：(1)弄清题意，正确理解，准确把握题目条件中的数量关系，必要时可用图表辅助分析(2)用字母表示问
3、题中的未知数(3)将题设条件中的语句都“翻译”成含有“字母”的代数式(4)寻找等量关系，列出方程组,热点看台 快速提升,热点看台 快速提升,B,B,热点看台 快速提升,热点二 一次方程(组)解的概念 热点搜索 使一次方程(组)成立的未知数的值叫做一次方程(组)的解解题依据是方程的定义，解题方法是把方程(组)的解代入原方程(组)，转化为关于待定系数的方程(组),热点看台 快速提升,k2,B,热点看台 快速提升,热点三 解一次方程(组) 热点搜索 对于一元一次方程的解法的考查，一般比较基础注意按照以下步骤即可：去分母、去括号、移项、合并同类项、系数化为1.对二元一次方程组的考查主要突出“消元”思想
4、，题目一般不难，系数比较简单，主要考查方法(加减消元法和代入消元法)的掌握,热点看台 快速提升,答案：x4,答案：,答案：,热点看台 快速提升,热点四 一次方程(组)的应用 热点搜索 列方程(组)解应用题是每年中考必考题目，形式多样解决此类问题的关键是要先找到等量关系，再依题意列出方程，重点在于平时积累一元一次方程、二元一次方程组的建模与应用能力,热点看台 快速提升,典例分析4 (2013四川凉山州)根据图中给出的信息，解答下列问题： (1)放入一个小球水面升高_ cm，放入一个大球水面升高_ cm. (2)如果要使水面上升到50 cm，应放入大球、小球各多少个？,解析 首先观察图形，根据放入
5、小球和大球的个数以及水面升高的高度得到分别放入一个小球和一个大球时，水面上升的高度接下来根据前面得到的结论结合题意设出恰当的未知数，列出关于未知数的二元一次方程组，即可解决问题,热点看台 快速提升,热点看台 快速提升,解：(1)甲每月应纳税所得额：40003500500(元)， 甲每月应缴纳的个人所得税为：5003%15(元) 乙每月应纳税所得额：(60003500)2500(元)， 乙每月应缴纳的个人所得税为：15003%100010%145(元) (2)若丙每月工资收入额为：150035005000(元)，则每月缴纳的个人所得税为： (50003500)3%45(元)95元，95元145元，所以丙纳税级数为2. 设丙每月工资收入额应为x元，则得： 15003%(x35001500)10%95 解得x5500 答：(1)甲、乙两人每月应缴纳的个人所得税分别为15元和145元(2)丙每月工资收入额应为5500元,热点看台 快速提升,9. (2013山东济南)某寄宿制学校有大、小两种类型的学生宿舍共50间，大宿舍每间可住8人，小宿舍每间可住6人该校360名住宿生恰好住满这50间宿舍求大、小宿舍各有多少间,热点看台 快速提升,热点看台 快速提升,D,答案：,答案：,
