1、备战2020中考数学解题方法专题研究专题5 几何变换法专题【方法简介】几何变换（geometric transformation）是指从具有几何结构之集合至其自身或其他此类集合的一种对射。几何变换是一种数学解题的方法思路。在几何的解题中，当题目给出的条件显得不够或者不明显时，我们可以将图形作一定的变换，这样将有利于发现问题的隐含条件，使问题得以突破。在几何题或代数几何综合题的解证过程中，经常会使用几何变换的观点来解决问题。从图形的特点出发，利用几何变换，可将图形的全部或一部分移动到一个新的位置，构成一个新的关系，从而使问题获得解决。这种几何变换不改变被移动部分图形的形状和大小，而只是它的位置发
2、生了变化，这种移动有利于找出图形之间的关系，从而使解题更为简捷。移动图形一般有三种方法：（1）平移法；（2）旋转法：利用旋转变换；（3）对称：可利用中心对称和轴对称。【真题演练】1. （ 山东青岛，3，3分）下列四个图形中，既是轴对称图形又是中心对称图形的是（）A. B. C. D.2. 新疆建设兵团，5，5分）如图所示，将一个含30角的直角三角板ABC绕点A旋转，使得点B，A，C在同一条直线上，则三角板ABC旋转的度数是（ ）A60 B90 C120 D1503. (2019，山西，3分）如图，在ABC中，BAC=90，AB=AC=10cm，点D为ABC内一点，BAD=15，AD=6cm，连
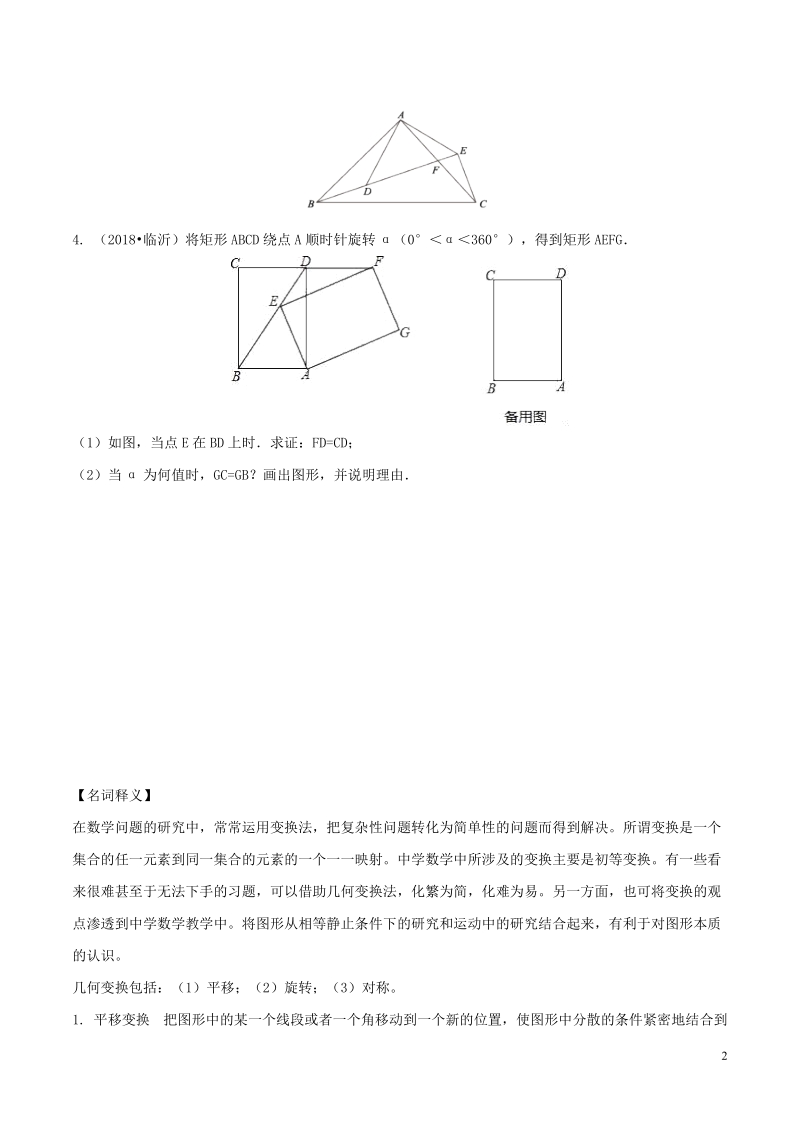
3、接BD，将ABD绕点A逆时针方向旋转，使AB与AC重合，点D的对应点E，连接DE，DE交AC于点F，则CF的长为 cm.4. （2018临沂）将矩形ABCD绕点A顺时针旋转（0360），得到矩形AEFG（1）如图，当点E在BD上时求证：FD=CD；（2）当为何值时，GC=GB？画出图形，并说明理由【名词释义】在数学问题的研究中，常常运用变换法，把复杂性问题转化为简单性的问题而得到解决。所谓变换是一个集合的任一元素到同一集合的元素的一个一一映射。中学数学中所涉及的变换主要是初等变换。有一些看来很难甚至于无法下手的习题，可以借助几何变换法，化繁为简，化难为易。另一方面，也可将变换的观点渗透到中学数
4、学教学中。将图形从相等静止条件下的研究和运动中的研究结合起来，有利于对图形本质的认识。几何变换包括：（1）平移；（2）旋转；（3）对称。1.平移变换 把图形中的某一个线段或者一个角移动到一个新的位置，使图形中分散的条件紧密地结合到一起。一般有2种方法：其一是平移已知条件，其二是平移所求问题，把所求问题转化，其实就是逆向证明。几何题多数都是逆向思考的。2.旋转变换 把平面图形绕旋转中心,旋转一个定角，使分散的条件集中在一起. 3.对称变换 通过作关于某一直线或一点的对称图，把图形中的图形对称到另一个位置上，使分散的条件集中在一起。当出现以下两种情况时，经常考虑用此变换：1.出现了明显的轴对称、中
5、心对称条件时。2.出现了明显的垂线条件时。【典例示例】例题1：（ 四川省绵阳市，17，3分）如图，点O是边长为的等边ABC的内心，将OBC绕点O逆时针旋转30得到OB1C1，B1C1交BC于点D，B1C1交AC于点E，则DE_例题2：（2019湖北省咸宁市3分）如图，先有一张矩形纸片ABCD，AB4，BC8，点M，N分别在矩形的边AD，BC上，将矩形纸片沿直线MN折叠，使点C落在矩形的边AD上，记为点P，点D落在G处，连接PC，交MN于点Q，连接CM下列结论：CQCD；四边形CMPN是菱形；P，A重合时，MN2；PQM的面积S的取值范围是3S5其中正确的是（把正确结论的序号都填上）【强化巩固】
6、1. （2018黑龙江龙东）（3.00分）下列图形中，既是轴对称图形又是中心对称图形的是（）ABCD2. （2017山东聊城）如图，将ABC绕点C顺时针旋转，使点B落在AB边上点B处，此时，点A的对应点A恰好落在BC边的延长线上，下列结论错误的（）ABCB=ACABACB=2BCBCA=BACDBC平分BBA3. （2019湖北省荆门市3分）如图，RtOCB的斜边在y轴上，OC，含30角的顶点与原点重合，直角顶点C在第二象限，将RtOCB绕原点顺时针旋转120后得到OCB，则B点的对应点B的坐标是（）A（，1）B（1，）C（2，0）D（，0）4. （2019，山东枣庄，3分）如图，将ABC沿B
7、C边上的中线AD平移到ABC的位置已知ABC的面积为16，阴影部分三角形的面积9若AA1，则AD等于（）A2B3C4D5. （2019广西池河3分）如图，在平面直角坐标系中，A（2，0），B（0，1），AC由AB绕点A顺时针旋转90而得，则AC所在直线的解析式是6. （2018广西南宁）（8.00分）如图，在平面直角坐标系中，已知ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）（1）将ABC向下平移5个单位后得到A1B1C1，请画出A1B1C1；（2）将ABC绕原点O逆时针旋转90后得到A2B2C2，请画出A2B2C2；（3）判断以O，A1，B为顶点的三角形的形状（无须说明理
8、由）7. （ 四川省巴中市，26，10分）如图，方格中每个小正方形的边长都是单位1，ABC在平面直角坐标系中的位置如图.（1）画出将ABC向右平移2个单位得到的A1B1C1；（2）画出将ABC绕点O顺时针方向旋转900得到的A2B2C2；（3）求A1B1C1与A2B2C2重合部分的面积.8. （2018自贡）如图，已知AOB=60，在AOB的平分线OM上有一点C，将一个120角的顶点与点C重合，它的两条边分别与直线OA、OB相交于点D、E（1）当DCE绕点C旋转到CD与OA垂直时（如图1），请猜想OE+OD与OC的数量关系，并说明理由；（2）当DCE绕点C旋转到CD与OA不垂直时，到达图2的位置，（1）中的结论是否成立？并说明理由；（3）当DCE绕点C旋转到CD与OA的反向延长线相交时，上述结论是否成立？请在图3中画出图形，若成立，请给于证明；若不成立，线段OD、OE与OC之间又有怎样的数量关系？请写出你的猜想，不需证明6
